03.有监督算法——决策树
1.决策树算法
决策树算法可以做分类,也可以做回归
决策树的训练与测试:
训练阶段:从给定的训练集构造出一棵树(从根节点开始选择特征,如何进行特征切分)
测试阶段:根据构造出来的树模型从上到下走一遍
一旦决策树构建好了,那么分类或预测任务就变得简单。难点在于如何构造出一颗树。或者说难点在于如何对数据特征进行重要程度的排序。
建立决策树的关键在于在当前状态下选择哪个属性作为分类依据。根据不同的目标函数,建立决策树主要有以下三种算法:
1.1. ID3(Iterative Dichotomiser)
熵:表示随机变量不确定性的度量,可以理解成物体内部的混乱程度。
信息熵:
H ( D ) = − ∑ k = 1 K ∣ C k ∣ ∣ D ∣ log 2 ∣ C k ∣ ∣ D ∣ {\rm{H(D) = - }}\sum\limits_{{\rm{k}} = 1}^K {{{|{C_{_k}}|} \over {|D|}}{{\log }_2}} {{|{C_{_k}}|} \over {|D|}} H(D)=−k=1∑K∣D∣∣Ck∣log2∣D∣∣Ck∣
其中,K是类别,D是数数据集,Ck是类别K下的数据集。
信息增益:表示特征X使得类Y的不确定性减小的程度(表示分类后的专一性,希望分类后的结果是同类在一起)
条件熵:
H ( D ∣ A ) = ∑ i = 1 n ∣ D i ∣ ∣ D ∣ H ( D i ) {\rm{H(D|A) = }}\sum\limits_{{\rm{i}} = 1}^n {{{|{D_i}|} \over {|D|}}H({D_i})} H(D∣A)=i=1∑n∣D∣∣Di∣H(Di)
其中,A是特征,i是特征取值。
信息增益构造决策树的步骤:
1.根据不同分类特征,求出信息增益,并找出信息增益最大的特征作为当前的决策结点
2.更新子集,在自己中选取新的特征,求信息增益的最大的特征
3.若划分的子集只包含单一特征,则为分支的叶子结点
缺点:
- ID3没有剪枝策略,容易过拟合;
- 信息增益准则对可取值数目较多的特征有所偏好,类似“编号”的特征其信息增益接近于1;
- 只能用于处理离散分布的特征;
- 没有考虑缺失值。
这么多缺点,那么有没有改进呢——C4.5
1.2. C4.5
C4.5是ID3算法的改进。相比ID3 选择属性用的是子树的信息增益,C4.5用的是信息增益率
此外,C4.5还有以下用途:
- 在决策树构造过程中,进行剪枝
- 对非离散数据也能进行处理
- 还能处理不完整数据
信息增益: g ( D , A ) = H ( D ) − H ( D ∣ A ) g({\rm{D,A}}){\rm{ = H(D) - H(D|A)}} g(D,A)=H(D)−H(D∣A)
信息增益率: g R ( D , A ) = g ( D , A ) H A ( D ) {g_R}({\rm{D,A}}){\rm{ = }}{{g(D,A)} \over {{H_A}(D)}} gR(D,A)=HA(D)g(D,A)
其中,公式 H ( D ) = − ∑ k = 1 K ∣ C k ∣ ∣ D ∣ log 2 ∣ C k ∣ ∣ D ∣ {\rm{H(D) = - }}\sum\limits_{{\rm{k}} = 1}^K {{{|{C_{_k}}|} \over {|D|}}{{\log }_2}} {{|{C_{_k}}|} \over {|D|}} H(D)=−k=1∑K∣D∣∣Ck∣log2∣D∣∣Ck∣,n是特征A的取值个数
注意:决策树 过拟合风险很大,理论上可以将数据完全分开。所以为了防止过拟合,就要进行剪枝操作:
- 预剪枝:边建立决策树边进行剪枝的操作
- 后剪枝:当建立完决策树 后进行剪枝操作
后剪枝:通过一定的衡量标准,具体来说:C4.5采用的悲观剪枝方法,用递归的方式从低往上针对每一个非叶子节点,评估用一个最佳叶子节点去代替这课子树是否有益。如果剪枝后与剪枝前相比其错误率是保持或者下降,则这棵子树就可以被替换掉。
后剪枝决策树的欠拟合风险很小,泛化性能往往优于预剪枝决策树
1.3. CART(Classification And Regression Tree)
Classification And Regression Tree(CART)是决策树中的一种。
这种决策树用基尼指数来选择属性(分类),或者用均方差来选择属性(回归)。
基尼指数:
G i n i ( p ) = ∑ k = 1 K p k ( 1 − p k ) {\rm{G}}ini(p) = \sum\limits_{k = 1}^K {{p_k}} (1 - {p_k}) Gini(p)=k=1∑Kpk(1−pk)
如果目标变量是离散的,称为分类树。最后取叶子结点的众数做分类结果。
如果目标变量是连续的,称为回归树。连续性目标没有类别概念,因此不能用熵进行计算,但是我们可以考虑另一种衡量物体内部混乱程度的指标:方差
对于任意划分特征A,对应的任意划分点s两边划分成数据集D1和D2,求出使D1和D2各自集合的均方差最小,同时D1和D2的均方差之和最小所对应的特征和特征值划分点。表达式为:
min a , s [ min c 1 ∑ x i ∈ D 1 n ( y i − c 1 ) 2 + min c 2 ∑ x i ∈ D 2 n ( y i − c 2 ) 2 ] {\min _{a,s}}[{\min _{{c_1}}}\sum\limits_{{x_i} \in {D_1}}^n {{{({y_i} - {c_1})}^2} + {{\min }_{c2}}\sum\limits_{{x_i} \in {D_2}}^n {{{({y_i} - {c_2})}^2}} } ] a,smin[c1minxi∈D1∑n(yi−c1)2+minc2xi∈D2∑n(yi−c2)2]
其中, c 1 {{c_1}} c1为 D 1 {{D_1}} D1数据集的样本输出均值, c 2 {{c_2}} c2为 D 2 {{D_2}} D2数据集的样本输出均值
相关文章:

03.有监督算法——决策树
1.决策树算法 决策树算法可以做分类,也可以做回归 决策树的训练与测试: 训练阶段:从给定的训练集构造出一棵树(从根节点开始选择特征,如何进行特征切分) 测试阶段:根据构造出来的树模型从上…...
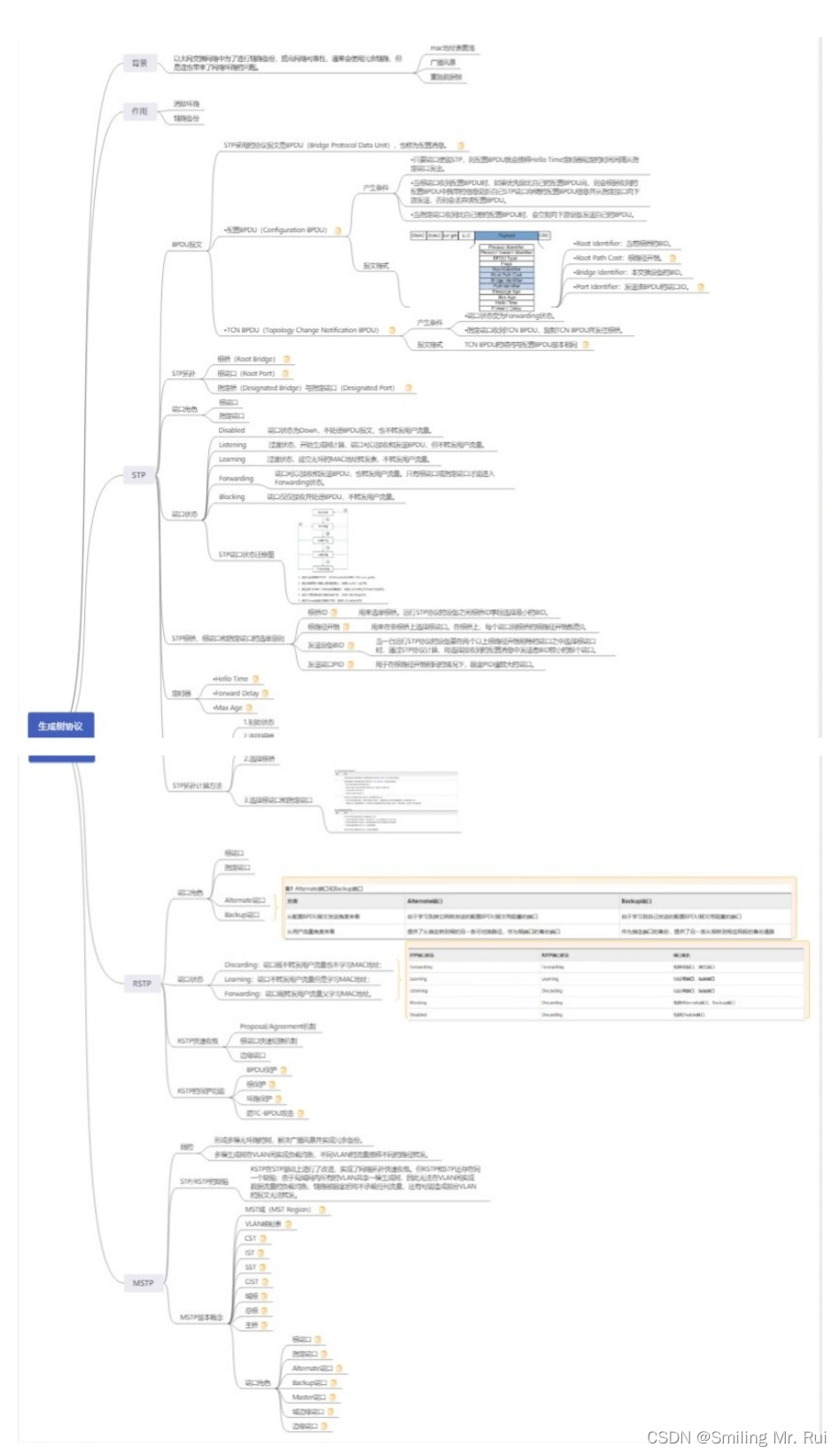
网络协议详解之STP
目录 一、STP协议(生成树) 1.1 生成树协议核心知识点: 1.2 生成树协议与导致问题: 生成树含义: 1.3 802.1D 规则: 802.1D 缺点: 1.4 PVST cisco私有 1.5 PVST 1.6 快速生成树 快速的原…...
Eltima USB Network Gate 10.0 Crack
USB Network Gate -通过网络共享USB 设备 USB Network Gate (前身为以太网USB控制器USB) 轻松的通过网络(Internet/LAN/WAN)分享您的一个或者多个连接到您计算机的USB设备。 无论您身处异国还是近在隔壁办公室,您都可以轻松使用远程扫描仪、打印机、摄像头、调制解…...
)
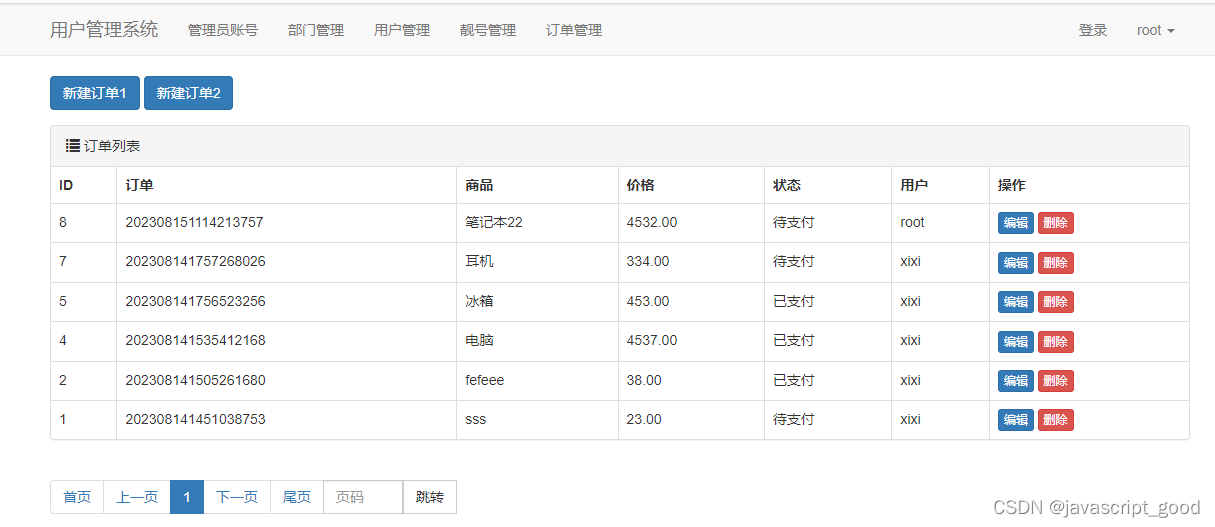
SpringCloudGateway网关实战(一)
SpringCloudGateway网关实战(一) 目前对cloud的gateway功能还是不太熟悉,因此特意新建了对应的应用来尝试网关功能。 网关模块搭建 首先我们新建一个父模块用于添加对应的springboot依赖和cloud依赖。本模块我们的配置读取使用的是nacos&a…...
django中使用ajax发送请求
1、ajax简单介绍 浏览器向网站发送请求时 是以URL和表单的形式提交的post 或get 请求,特点是:页面刷新 除此之外,也可以基于ajax向后台发送请求(异步) 依赖jQuery 编写ajax代码 $.ajax({url: "发送的地址"…...

C++之std::list<string>::iterator迭代器应用实例(一百七十九)
简介: CSDN博客专家,专注Android/Linux系统,分享多mic语音方案、音视频、编解码等技术,与大家一起成长! 优质专栏:Audio工程师进阶系列【原创干货持续更新中……】🚀 人生格言: 人生…...

VSCode好用的插件
文章目录 前言1.Snippet Creator & easy snippet(自定义代码)2.Indent Rainbow(代码缩进)3.Chinese (Simplified) Language Pack(中文包)4.Path Intellisense(路径提示)5.Beauti…...
)
js实现滚轮滑动到底部自动加载(完整版)
这里我们用vue实现(原生js相似), 这里我们用一个div当作一个容器; <div class="JL" @scroll="onScroll" ref="inin"> <div v-for="(item,index) in this.list" :key="index" > ....…...
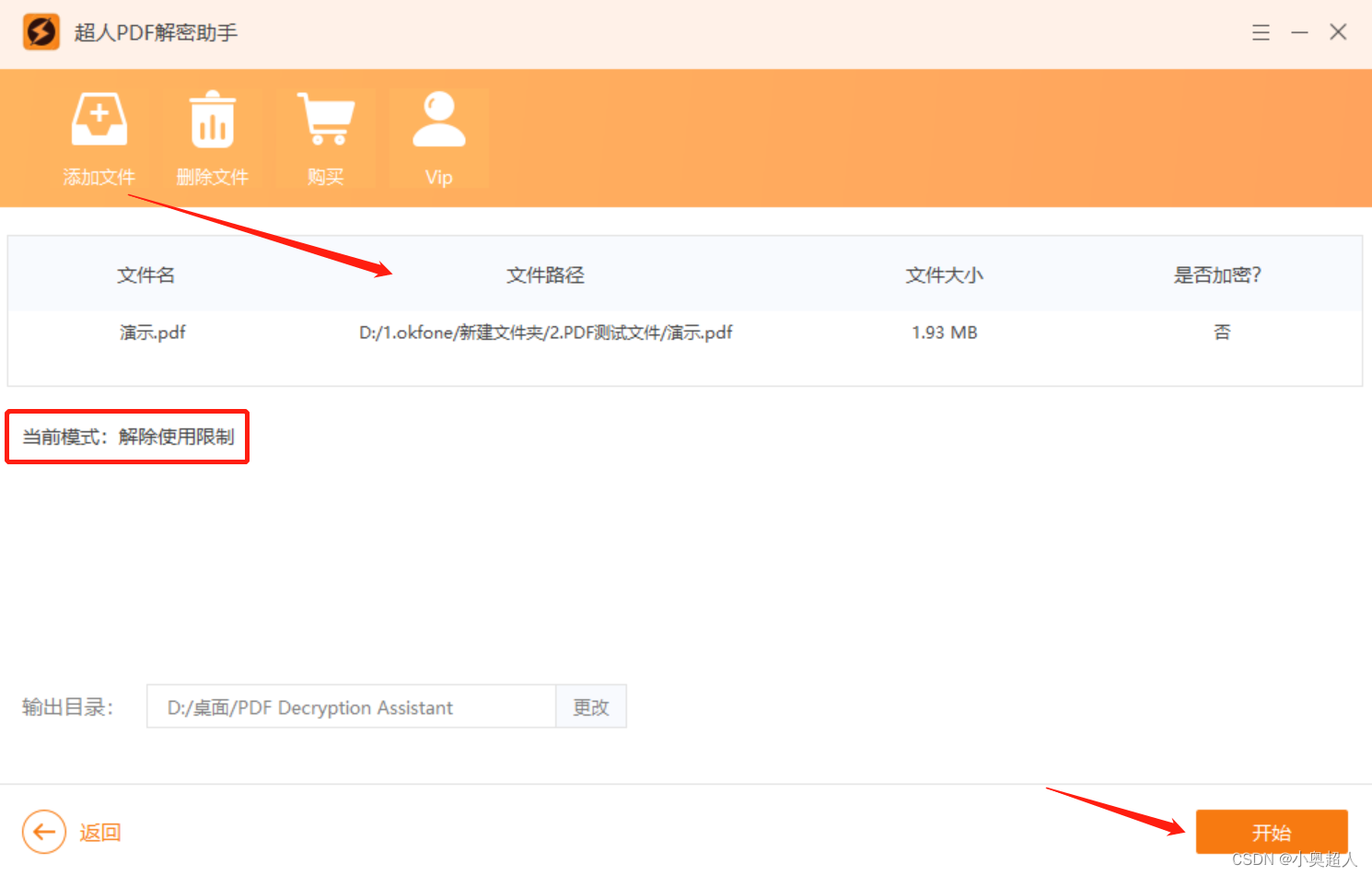
如何限制PDF打印?限制清晰度?
想要限制PDF文件的打印功能,想要限制PDF文件打印清晰度,都可以通过设置限制编辑来达到目的。 打开PDF编辑器,找到设置限制编辑的界面,切换到加密状态,然后我们就看到 有印刷许可。勾选【权限密码】输入一个PDF密码&am…...

python计算模板图像与原图像各区域的相似度
目录 1、解释说明: 2、使用示例: 3、注意事项: 1、解释说明: 在Python中,我们可以使用OpenCV库进行图像处理和计算机视觉任务。其中,模板匹配是一种常见的方法,用于在一幅图像中识别出与给定…...
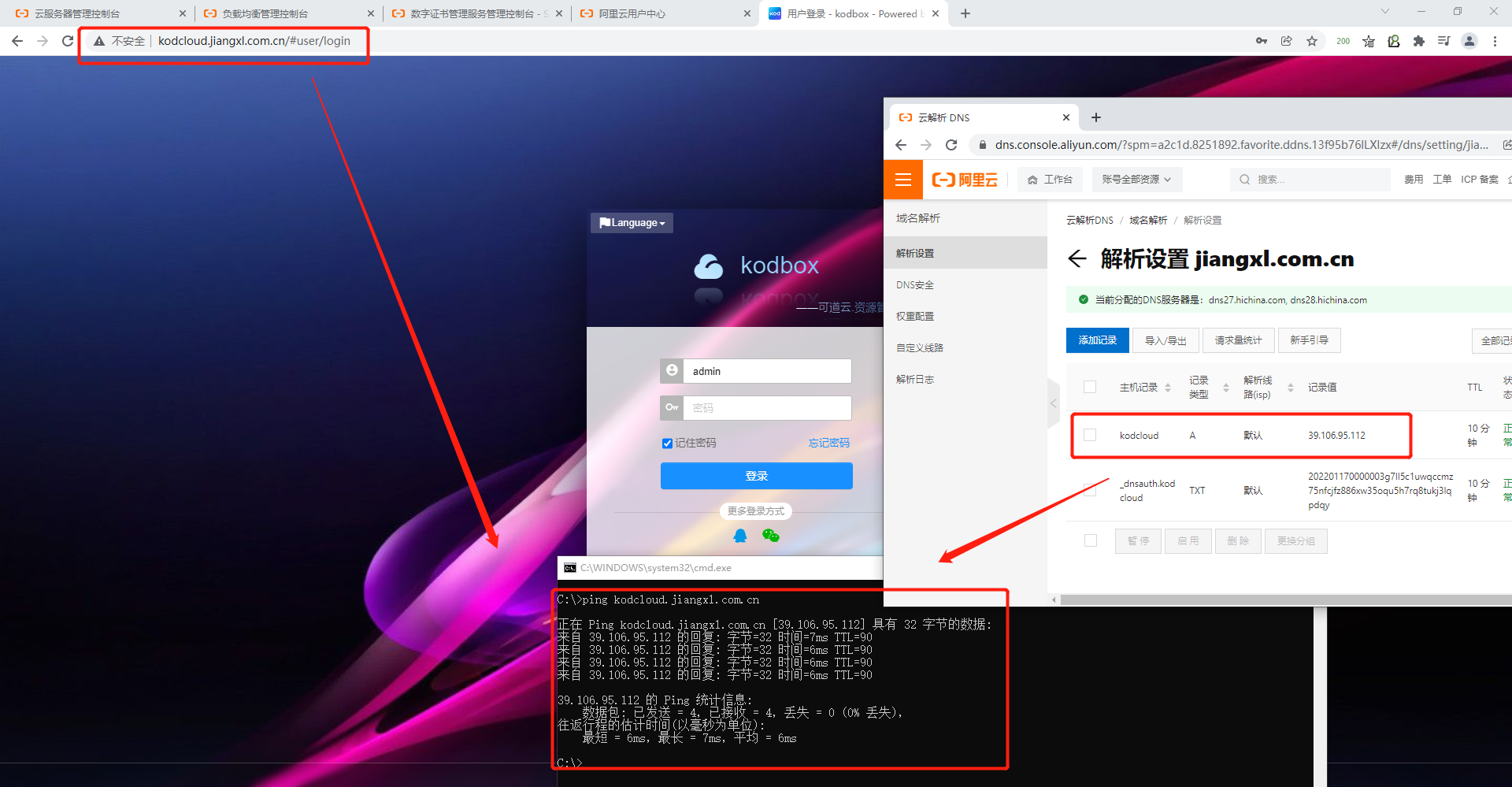
阿里云云解析DNS核心概念与应用
文章目录 1.DNS解析基本概念1.1.DNS基本介绍1.2.域名的分层结构1.3.DNS解析原理1.4.DNS递归查询和迭代查询的区别1.5.DNS常用的解析记录 2.使用DNS云解析将域名与SLB公网IP进行绑定2.1.进入云解析DNS控制台2.2.添加域名解析记录2.3.验证解析是否生效 1.DNS解析基本概念 DNS官方…...
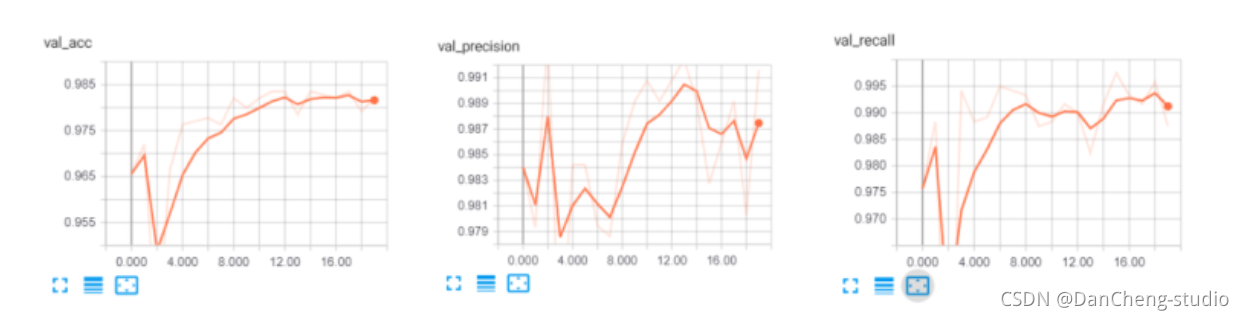
计算机竞赛 垃圾邮件(短信)分类算法实现 机器学习 深度学习
文章目录 0 前言2 垃圾短信/邮件 分类算法 原理2.1 常用的分类器 - 贝叶斯分类器 3 数据集介绍4 数据预处理5 特征提取6 训练分类器7 综合测试结果8 其他模型方法9 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 垃圾邮件(短信)分类算…...

compositionAPI
面试题:composition api相比于option api有哪些优势? 不同于reactivity api,composition api提供的函数很多是与组件深度绑定的,不能脱离组件而存在。 1. setup // component export default {setup(props, context){// 该函数在…...

vscode配置调试环境-windows系统
1. 下载Vscode 下载网址code.visualstudio.com 2. 安装vscode 直打开下载好的.exe文件进行安装即可 3.安装插件 4下载mingw编译器 4.1下载 下载网址sourceforge.net/projects/mingw-w64/files/ 下拉找到该位置,下载圈中的版本。下载速度有点慢 临时下载地址 htt…...

智慧城市能实现嘛?数字孪生又在其中扮演什么角色?
数字孪生智慧城市是将数字孪生技术与城市智能化相结合的新兴概念,旨在通过实时数字模拟城市运行,优化城市管理与服务,创造更智能、高效、可持续的城市环境。 在智慧城市中,数字孪生技术可以实时收集、分析城市各个方面的数据&…...

【置顶帖】关于博主/关于博客/博客大事记
关于博主 ● 信息安全从业者 ● 注册信息安全认证专家资质 ● CSDN认证业界专家、安全博客专家 、全栈安全领域优质创作者 ● 中国信通院【2021-GOLF IT新治理领导力论坛】演讲嘉宾 ● 安世加【2021-EISS企业信息安全峰会-上海】演讲嘉宾 ● CSDN【2022-隐私计算论坛】演讲嘉宾…...

华为数通方向HCIP-DataCom H12-821题库(单选题:01-20)
第01题 下面关于OSPF邻居关系和邻接关系描述正确的是 A、邻接关系由 OSPF的 DD 报文维护 B、OSPF 路由器在交换 Hello 报文之前必须建立邻接关系 C、邻居关系是从邻接关系中选出的为了交换路由信息而形成的关系 D、并非所有的邻居关系都可以成为邻接关系 答案:D 解析…...

Java【手撕双指针】LeetCode 11. “盛水最多的容器“, 图文详解思路分析 + 代码
文章目录 前言一、盛水最多的容器1, 题目2, 思路分析3, 代码展示 前言 各位读者好, 我是小陈, 这是我的个人主页, 希望我的专栏能够帮助到你: 📕 JavaSE基础: 基础语法, 类和对象, 封装继承多态, 接口, 综合小练习图书管理系统等 📗 Java数据结构: 顺序表…...

vue3——递归组件的使用
该文章是在学习 小满vue3 课程的随堂记录示例均采用 <script setup>,且包含 typescript 的基础用法 一、使用场景 递归组件 的使用场景,如 无限级的菜单 ,接下来就用菜单的例子来学习 二、具体使用 先把菜单的基础内容写出来再说 父…...

【爬虫练习之glidedsky】爬虫-基础1
题目 链接 爬虫的目标很简单,就是拿到想要的数据。 这里有一个网站,里面有一些数字。把这些数字的总和,输入到答案框里面,即可通过本关。 思路 找到调用接口 分析response 代码实现 import re import requestsurl http://www.…...

MongoDB学习和应用(高效的非关系型数据库)
一丶 MongoDB简介 对于社交类软件的功能,我们需要对它的功能特点进行分析: 数据量会随着用户数增大而增大读多写少价值较低非好友看不到其动态信息地理位置的查询… 针对以上特点进行分析各大存储工具: mysql:关系型数据库&am…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

渲染学进阶内容——模型
最近在写模组的时候发现渲染器里面离不开模型的定义,在渲染的第二篇文章中简单的讲解了一下关于模型部分的内容,其实不管是方块还是方块实体,都离不开模型的内容 🧱 一、CubeListBuilder 功能解析 CubeListBuilder 是 Minecraft Java 版模型系统的核心构建器,用于动态创…...

MVC 数据库
MVC 数据库 引言 在软件开发领域,Model-View-Controller(MVC)是一种流行的软件架构模式,它将应用程序分为三个核心组件:模型(Model)、视图(View)和控制器(Controller)。这种模式有助于提高代码的可维护性和可扩展性。本文将深入探讨MVC架构与数据库之间的关系,以…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...
Reasoning over Uncertain Text by Generative Large Language Models
https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829https://ojs.aaai.org/index.php/AAAI/article/view/34674/36829 1. 概述 文本中的不确定性在许多语境中传达,从日常对话到特定领域的文档(例如医学文档)(Heritage 2013;Landmark、Gulbrandsen 和 Svenevei…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

PAN/FPN
import torch import torch.nn as nn import torch.nn.functional as F import mathclass LowResQueryHighResKVAttention(nn.Module):"""方案 1: 低分辨率特征 (Query) 查询高分辨率特征 (Key, Value).输出分辨率与低分辨率输入相同。"""def __…...

DingDing机器人群消息推送
文章目录 1 新建机器人2 API文档说明3 代码编写 1 新建机器人 点击群设置 下滑到群管理的机器人,点击进入 添加机器人 选择自定义Webhook服务 点击添加 设置安全设置,详见说明文档 成功后,记录Webhook 2 API文档说明 点击设置说明 查看自…...
