2023国赛数学建模思路 - 案例:感知机原理剖析及实现
文章目录
- 1 感知机的直观理解
- 2 感知机的数学角度
- 3 代码实现
- 4 建模资料
# 0 赛题思路
(赛题出来以后第一时间在CSDN分享)
https://blog.csdn.net/dc_sinor?type=blog
1 感知机的直观理解
感知机应该属于机器学习算法中最简单的一种算法,其原理可以看下图:
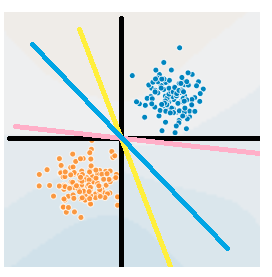
比如说我们有一个坐标轴(图中的黑色线),横的为x1轴,竖的x2轴。图中的每一个点都是由(x1,x2)决定的。如果我们将这张图应用在判断零件是否合格上,x1表示零件长度,x2表示零件质量,坐标轴表示零件的均值长度和均值重量,并且蓝色的为合格产品,黄色为劣质产品,需要剔除。那么很显然如果零件的长度和重量都大于均值,说明这个零件是合格的。也就是在第一象限的所有蓝色点。反之如果两项都小于均值,就是劣质的,比如在第三象限的黄色点。
在预测上很简单,拿到一个新的零件,我们测出它的长度x1,质量x2,如果两项都大于均值,说明零件合格。这就是我们人的人工智能。
那么程序怎么知道长度重量都大于均值的零件就是合格的呢?
或者说
它是怎么学会这个规则的呢?
程序拿到手的是当前图里所有点的信息以及标签,也就是说它知道所有样本x的坐标为(x1, x2),同时它属于蓝色或黄色。对于目前手里的这些点,要是能找到一条直线把它们分开就好了,这样我拿到一个新的零件,知道了它的质量和重量,我就可以判断它在线的哪一侧,就可以知道它可能属于好的或坏的零件了。例如图里的黄、蓝、粉三条线,都可以完美地把当前的两种情况划分开。甚至x1坐标轴或x2坐标轴都能成为一个划分直线(这两个直线均能把所有点正确地分开)。
读者也看到了,对于图中的两堆点,我们有无数条直线可以将其划分开,事实上我们不光要能划分当前的点,当新来的点进来是,也要能很好地将其划分,所以哪条线最好呢?
怎样一条直线属于最佳的划分直线?实际上感知机无法找到一条最佳的直线,它找到的可能是图中所有画出来的线,只要能把所有的点都分开就好了。
得出结论:
如果一条直线能够不分错一个点,那就是一条好的直线
进一步来说:
如果我们把所有分错的点和直线的距离求和,让这段求和的举例最小(最好是0,这样就表示没有分错的点了),这条直线就是我们要找的。
2 感知机的数学角度
首先我们确定一下终极目标:甭管找最佳划分直线啥中间乱七八糟的步骤,反正最后生成一个函数f(x),当我们把新的一个数据x扔进函数以后,它会预测告诉我这是蓝的还是黄的,多简单啊。所以我们不要去考虑中间过程,先把结果定了。
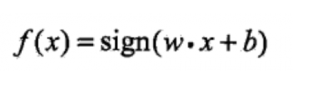
瞧,f(x)不是出来了嘛,sign是啥?wx+b是啥?别着急,我们再看一下sigin函数是什么。
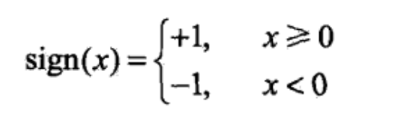
sign好像很简单,当x大于等于0,sign输出1,否则输出-1。那么往前递归一下,wx+b如果大于等于0,f(x)就等于1,反之f(x)等于-1。
那么wx+b是啥?
它就是那条最优的直线。我们把这个公式放在二维情况下看,二维中的直线是这样定义的:y=ax+b。在二维中,w就是a,b还是b。所以wx+b是一条直线(比如说本文最开始那张图中的蓝线)。如果新的点x在蓝线左侧,那么wx+b<0,再经过sign,最后f输出-1,如果在右侧,输出1。等等,好像有点说不通,把情况等价到二维平面中,y=ax+b,只要点在x轴上方,甭管点在线的左侧右侧,最后结果都是大于0啊,这个值得正负跟线有啥关系?emmm….其实wx+b和ax+b表现直线的形式一样,但是又稍有差别。我们把最前头的图逆时针旋转45度,蓝线是不是变成x轴了?哈哈这样是不是原先蓝线的右侧变成了x轴的上方了?其实感知机在计算wx+b这条线的时候,已经在暗地里进行了转换,使得用于划分的直线变成x轴,左右侧分别为x轴的上方和下方,也就成了正和负。
那么,为啥是wx+b,而不叫ax+b?
在本文中使用零件作为例子,上文使用了长度和重量(x1,x2)来表示一个零件的属性,所以一个二维平面就足够,那么如果零件的品质和色泽也有关系呢?那就得加一个x3表示色泽,样本的属性就变成了(x1,x2,x3),变成三维了。wx+b并不是只用于二维情况,在三维这种情况下,仍然可以使用这个公式。所以wx+b与ax+b只是在二维上近似一致,实际上是不同的东西。在三维中wx+b是啥?我们想象屋子里一个角落有蓝点,一个角落有黄点,还用一条直线的话,显然是不够的,需要一个平面!所以在三维中,wx+b是一个平面!至于为什么,后文会详细说明。四维呢?emmm…好像没法描述是个什么东西可以把四维空间分开,但是对于四维来说,应该会存在一个东西像一把刀一样把四维空间切成两半。能切成两半,应该是一个对于四维来说是个平面的东西,就像对于三维来说切割它的是一个二维的平面,二维来说是一个一维的平面。总之四维中wx+b可以表示为一个相对于四维来说是个平面的东西,然后把四维空间一切为二,我们给它取名叫超平面。由此引申,在高维空间中,wx+b是一个划分超平面,这也就是它正式的名字。
正式来说:
wx+b是一个n维空间中的超平面S,其中w是超平面的法向量,b是超平面的截距,这个超平面将特征空间划分成两部分,位于两部分的点分别被分为正负两类,所以,超平面S称为分离超平面。
细节:
w是超平面的法向量:对于一个平面来说w就是这么定义的,是数学知识,可以谷歌补习一下
b是超平面的截距:可以按照二维中的ax+b理解
特征空间:也就是整个n维空间,样本的每个属性都叫一个特征,特征空间的意思是在这个空间中可以找到样本所有的属性组合

我们从最初的要求有个f(x),引申到能只输出1和-1的sign(x),再到现在的wx+b,看起来越来越简单了,只要能找到最合适的wx+b,就能完成感知机的搭建了。前文说过,让误分类的点距离和最大化来找这个超平面,首先我们要放出单独计算一个点与超平面之间距离的公式,这样才能将所有的点的距离公式求出来对不?

先看wx+b,在二维空间中,我们可以认为它是一条直线,同时因为做过转换,整张图旋转后wx+b是x轴,那么所有点到x轴的距离其实就是wx+b的值对不?当然了,考虑到x轴下方的点,得加上绝对值->|wx+b|,求所有误分类点的距离和,也就是求|wx+b|的总和,让它最小化。很简单啊,把w和b等比例缩小就好啦,比如说w改为0.5w,b改为0.5b,线还是那条线,但是值缩小两倍啦!你还不满意?我可以接着缩!缩到0去!所以啊,我们要加点约束,让整个式子除以w的模长。啥意思?就是w不管怎么样,要除以它的单位长度。如果我w和b等比例缩小,那||w||也会等比例缩小,值一动不动,很稳。没有除以模长之前,|wx+b|叫函数间隔,除模长之后叫几何间隔,几何间隔可以认为是物理意义上的实际长度,管你怎么放大缩小,你物理距离就那样,不可能改个数就变。在机器学习中求距离时,通常是使用几何间隔的,否则无法求出解。

对于误分类的数据,例如实际应该属于蓝色的点(线的右侧,y>0),但实际上预测出来是在左侧(wx+b<0),那就是分错了,结果是负,这时候再加个符号,结果就是正了,再除以w的模长,就是单个误分类的点到超平面的举例。举例总和就是所有误分类的点相加。
上图最后说不考虑除以模长,就变成了函数间隔,为什么可以这么做呢?不考虑wb等比例缩小这件事了吗?上文说的是错的吗?
有一种解释是这样说的:感知机是误分类驱动的算法,它的终极目标是没有误分类的点,如果没有误分类的点,总和距离就变成了0,w和b值怎样都没用。所以几何间隔和函数间隔在感知机的应用上没有差别,为了计算简单,使用函数间隔。

以上是损失函数的正式定义,在求得划分超平面的终极目标就是让损失函数最小化,如果是0的话就相当完美了。

感知机使用梯度下降方法求得w和b的最优解,从而得到划分超平面wx+b,关于梯度下降及其中的步长受篇幅所限可以自行谷歌。
3 代码实现
#coding=utf-8
#Author:Dodo
#Date:2018-11-15
#Email:lvtengchao@pku.edu.cn
'''
数据集:Mnist
训练集数量:60000
测试集数量:10000
------------------------------
运行结果:
正确率:81.72%(二分类)
运行时长:78.6s
'''
import numpy as np
import time
def loadData(fileName):'''加载Mnist数据集:param fileName:要加载的数据集路径:return: list形式的数据集及标记'''print('start to read data')# 存放数据及标记的listdataArr = []; labelArr = []# 打开文件fr = open(fileName, 'r')# 将文件按行读取for line in fr.readlines():# 对每一行数据按切割福','进行切割,返回字段列表curLine = line.strip().split(',')# Mnsit有0-9是个标记,由于是二分类任务,所以将>=5的作为1,<5为-1if int(curLine[0]) >= 5:labelArr.append(1)else:labelArr.append(-1)#存放标记#[int(num) for num in curLine[1:]] -> 遍历每一行中除了以第一哥元素(标记)外将所有元素转换成int类型#[int(num)/255 for num in curLine[1:]] -> 将所有数据除255归一化(非必须步骤,可以不归一化)dataArr.append([int(num)/255 for num in curLine[1:]])#返回data和labelreturn dataArr, labelArr
def perceptron(dataArr, labelArr, iter=50):'''感知器训练过程:param dataArr:训练集的数据 (list):param labelArr: 训练集的标签(list):param iter: 迭代次数,默认50:return: 训练好的w和b'''print('start to trans')#将数据转换成矩阵形式(在机器学习中因为通常都是向量的运算,转换称矩阵形式方便运算)#转换后的数据中每一个样本的向量都是横向的dataMat = np.mat(dataArr)#将标签转换成矩阵,之后转置(.T为转置)。#转置是因为在运算中需要单独取label中的某一个元素,如果是1xN的矩阵的话,无法用label[i]的方式读取#对于只有1xN的label可以不转换成矩阵,直接label[i]即可,这里转换是为了格式上的统一labelMat = np.mat(labelArr).T#获取数据矩阵的大小,为m*nm, n = np.shape(dataMat)#创建初始权重w,初始值全为0。#np.shape(dataMat)的返回值为m,n -> np.shape(dataMat)[1])的值即为n,与#样本长度保持一致w = np.zeros((1, np.shape(dataMat)[1]))#初始化偏置b为0b = 0#初始化步长,也就是梯度下降过程中的n,控制梯度下降速率h = 0.0001#进行iter次迭代计算for k in range(iter):#对于每一个样本进行梯度下降#李航书中在2.3.1开头部分使用的梯度下降,是全部样本都算一遍以后,统一#进行一次梯度下降#在2.3.1的后半部分可以看到(例如公式2.6 2.7),求和符号没有了,此时用#的是随机梯度下降,即计算一个样本就针对该样本进行一次梯度下降。#两者的差异各有千秋,但较为常用的是随机梯度下降。for i in range(m):#获取当前样本的向量xi = dataMat[i]#获取当前样本所对应的标签yi = labelMat[i]#判断是否是误分类样本#误分类样本特诊为: -yi(w*xi+b)>=0,详细可参考书中2.2.2小节#在书的公式中写的是>0,实际上如果=0,说明改点在超平面上,也是不正确的if -1 * yi * (w * xi.T + b) >= 0:#对于误分类样本,进行梯度下降,更新w和bw = w + h * yi * xib = b + h * yi#打印训练进度print('Round %d:%d training' % (k, iter))#返回训练完的w、breturn w, b
def test(dataArr, labelArr, w, b):'''测试准确率:param dataArr:测试集:param labelArr: 测试集标签:param w: 训练获得的权重w:param b: 训练获得的偏置b:return: 正确率'''print('start to test')#将数据集转换为矩阵形式方便运算dataMat = np.mat(dataArr)#将label转换为矩阵并转置,详细信息参考上文perceptron中#对于这部分的解说labelMat = np.mat(labelArr).T#获取测试数据集矩阵的大小m, n = np.shape(dataMat)#错误样本数计数errorCnt = 0#遍历所有测试样本for i in range(m):#获得单个样本向量xi = dataMat[i]#获得该样本标记yi = labelMat[i]#获得运算结果result = -1 * yi * (w * xi.T + b)#如果-yi(w*xi+b)>=0,说明该样本被误分类,错误样本数加一if result >= 0: errorCnt += 1#正确率 = 1 - (样本分类错误数 / 样本总数)accruRate = 1 - (errorCnt / m)#返回正确率return accruRate
if __name__ == '__main__':#获取当前时间#在文末同样获取当前时间,两时间差即为程序运行时间start = time.time()#获取训练集及标签trainData, trainLabel = loadData('../Mnist/mnist_train.csv')#获取测试集及标签testData, testLabel = loadData('../Mnist/mnist_test.csv')#训练获得权重w, b = perceptron(trainData, trainLabel, iter = 30)#进行测试,获得正确率accruRate = test(testData, testLabel, w, b)#获取当前时间,作为结束时间end = time.time()#显示正确率print('accuracy rate is:', accruRate)#显示用时时长print('time span:', end - start)
4 建模资料
资料分享: 最强建模资料


相关文章:

2023国赛数学建模思路 - 案例:感知机原理剖析及实现
文章目录 1 感知机的直观理解2 感知机的数学角度3 代码实现 4 建模资料 # 0 赛题思路 (赛题出来以后第一时间在CSDN分享) https://blog.csdn.net/dc_sinor?typeblog 1 感知机的直观理解 感知机应该属于机器学习算法中最简单的一种算法,其…...
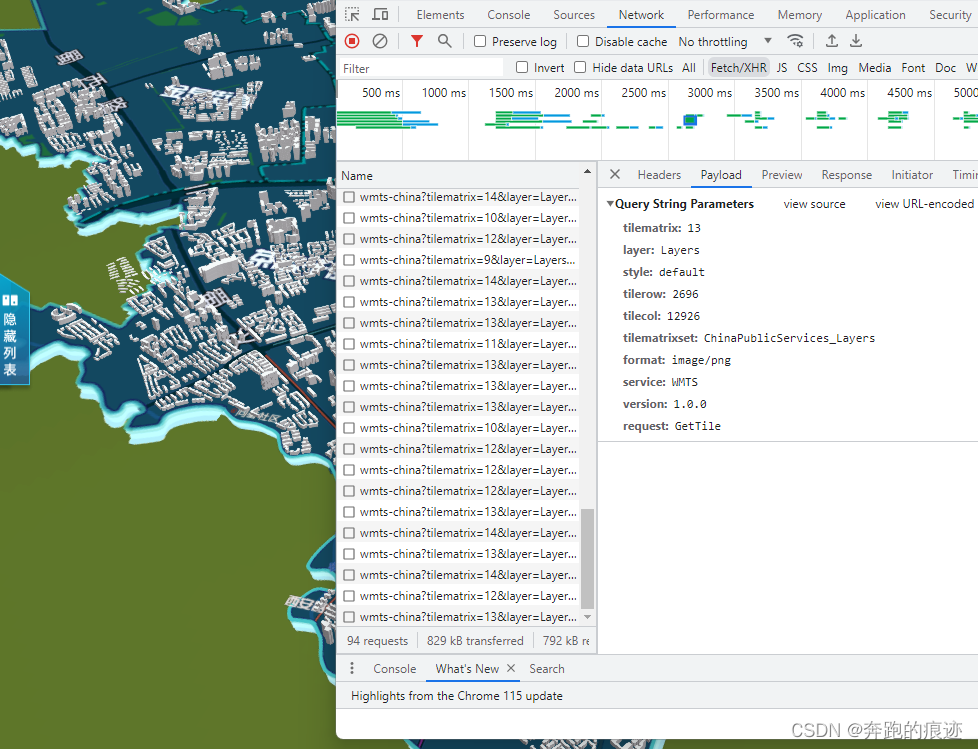
Cesium加载Supermap的wmts服务
最近使用cesium 加载supermap的wmts 服务,多次遇到加载异常与白页面问题,纠结好久最后才搞定[特此记录] 1、首先找到方法加载wmts 的api 文档 官方提示使用WebMapTileServiceImageryProvider加载wmts 2、然后编辑加载代码 //1.新建ImageryProviderlet…...
C/C++:C/C++在大数据时代的应用,以及C/C++程序员未来的发展路线
目录 1.C/C在大数据时代的应用 1.1:C/C数据处理 1.2:C/C数据库 1.3:C/C图像处理和计算机视觉 1.3.1:导读 2.C/C程序员未来的发展路线 2.1:图导 1.C/C在大数据时代的应用 C/C在大数据时代中仍然是一种被广泛应用的编…...
linux RabbitMQ-3.8.5 安装
软件版本操作系统CentOS Linux release 7.9.2009erlangerlang-23.0.2-1.el7.x86_64rabbitMQrabbitmq-server-3.8.5-1.el7 RabbitMQ的安装首先需要安装Erlang,因为它是基于Erlang的VM运行的。 RabbitMQ安装需要依赖:socat和logrotate,logrotate操作系统已经存在了&…...

单链表Single-LinkList
0、节点结构体定义 typedef struct LNode{int data;struct LNode *next;} Lnode, *LinkList; 1、初始化 bool InitList(LinkList &L) //初始化 {L new LNode;if(!L){return false;}L->next NULL;return true; } 2、创建 (1)头插法 void Cr…...

AI嵌入式全景:各厂商、系列和开发工具的综合概览
要看几个方面 1 算力: 2 支持何种模型: 3 是否支持可视化的窗口系统: 一般而言各个平台均采用linux操作系统,官方提供对应SDK,安装好后可使用硬件加速资源。 而且如果要使用其硬件加速,一般都要完成模型转…...
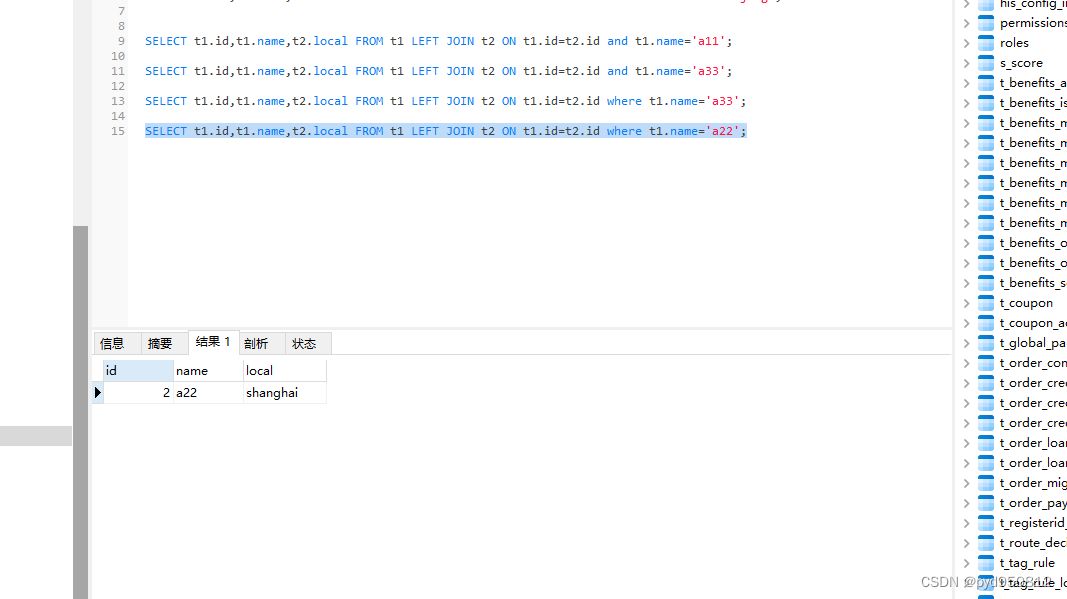
mysql Left Join on条件 where条件的用法区别
数据准备 SELECT t1.id,t1.name,t2.local FROM t1 LEFT JOIN t2 ON t1.idt2.id; 执行结果 SELECT t1.id,t1.name,t2.local FROM t1 LEFT JOIN t2 ON t1.idt2.id and t2.localbeijing; SELECT t1.id,t1.name,t2.local FROM t1 LEFT JOIN t2 ON t1.idt2.id where t2.localbeijing…...

Redis中的淘汰策略
前言 本文主要说明在Redis面临key过期和内存不足的情况时,可以采用什么策略进行解决问题。 Redis中是如何应对过期数据的 正如我们知道的Redis是基于内存的、单线程的一个中间件,在面对过期数据的时候,Redis并不会去直接把它从内存中进行剔…...

MyBatis进阶:掌握MyBatis动态SQL与模糊查询、结果映射,让你在面试中脱颖而出!!
目录 一、引言 二、MyBatis动态SQL 2.1.if元素使用 2.2.foreach元素使用 三、MyBatis模糊查询 ①使用#{字段名} ②使用${字段名} ③使用concat{%,#{字段名},%} 总结 四、MyBatis结果映射 4.1.案例演示 4.1.1.resultType进行结果映射 4.1.2.resultMap进行结果映射 …...

C++ 写入txt文件内容并追加内容
咨询通义千问的“C 写入txt文件内容并追加内容”: 可以使用ofstream类来写入txt文件内容。若想追加内容,可以使用ios::app标志来创建输出流对象,然后在写入时将其设置为ios::app。以下是一个示例代码: #include <iostream>…...

Leetcode---359周赛
题目列表 2828. 判别首字母缩略词 2829. k-avoiding 数组的最小总和 2830. 销售利润最大化 2831. 找出最长等值子数组 一、判断首字母缩略词 纯模拟,代码如下 class Solution { public:bool isAcronym(vector<string>& words, string s) {string tmp…...

Keras三种主流模型构建方式:序列模型、函数模型、子类模型开发实践,以真实烟雾识别场景数据为例
Keras和PyTorch是两个常用的深度学习框架,它们都提供了用于构建和训练神经网络的高级API。 Keras: Keras是一个高级神经网络API,可以在多个底层深度学习框架上运行,如TensorFlow和CNTK。以下是Keras的特点和优点: 优点…...

objective-v 获取iPhone系统当前时间字符串适配12小时制和24小时制
我们最开始获取系统当前时间,如下,这种方式存在一个问题,当iPhone关闭了24小时制时,获取的时间格式是:iPhone11上:20230822下午210568760;iPhone7 plus上:2023082240043851 PM&#…...

并查集及其简单应用
文章目录 一.并查集二.并查集的实现三.并查集的基本应用 一.并查集 并查集的逻辑结构:由多颗不相连通的多叉树构成的森林(一个这样的多叉树就是森林的一个连通分量) 并查集的元素(树节点)用0~9的整数表示,并查集可以表示如下: 并查集的物理存储结构:并查集一般采用顺序结构实…...
基于web的服装商城系统java网上购物商店jsp源代码mysql
本项目为前几天收费帮学妹做的一个项目,Java EE JSP项目,在工作环境中基本使用不到,但是很多学校把这个当作编程入门的项目来做,故分享出本项目供初学者参考。 一、项目描述 基于web的服装商城系统 系统有1权限:前台…...

.NET Core发布到IIS
项目介绍 1、开发工具Visual Studio 2017,语言C#,SQL SERVER,WIN10 2、本地IIS,手机上或其他用户在和本地在同一个局域网内访问,同时要把防火墙关掉 3、IIS全名Internet Information Services,用来发布网站 先决条件 安…...
Spring的基本概念
前言 Spring 究竟是什么?其实Spring简单来说就是一个包含众多工具方法的IOC容器。 那么什么是IOC呢? IoC Inversion of Control 翻译成中⽂是“控制反转”的意思. 既然Spring 是⼀个IoC(控制反转)容器,重点还在“容…...

设计模式之原型模式
文章目录 一、介绍二、实现步骤三、案例四、应用五、细胞分裂六、改造细胞分裂逻辑七、总结 一、介绍 原型模式属于创建型设计模式,用于创建重复的对象,且同时又保证了性能。 该设计模式的好处是将对象的创建与调用方分离。 其目的就是**根据一个对象…...

正则表达式在网页处理中的应用四则
正则表达式在网页处理中的应用四则 正则表达式(Regular Expression)为字符串模式匹配提供了一种高效、方便的方法。几乎所有高级语言都提供了对正则表达式的支持,或者提供了现成的代码库供调用。本文以ASP环境中常见的处理任务为例,介绍正则表达式的应用技巧。 一、检验密…...

ping使用方法
文章目录 1、Ping的基础知识2、Ping命令详解3、怎样使用Ping这命令来测试网络连通?4、如何用Ping命令来判断一条链路好坏?5、对Ping后返回信息的分析1.Request timed out2.Destination host Unreachable 1、Ping的基础知识 ping命令相信大家已经再熟悉不…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

Admin.Net中的消息通信SignalR解释
定义集线器接口 IOnlineUserHub public interface IOnlineUserHub {/// 在线用户列表Task OnlineUserList(OnlineUserList context);/// 强制下线Task ForceOffline(object context);/// 发布站内消息Task PublicNotice(SysNotice context);/// 接收消息Task ReceiveMessage(…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

【笔记】WSL 中 Rust 安装与测试完整记录
#工作记录 WSL 中 Rust 安装与测试完整记录 1. 运行环境 系统:Ubuntu 24.04 LTS (WSL2)架构:x86_64 (GNU/Linux)Rust 版本:rustc 1.87.0 (2025-05-09)Cargo 版本:cargo 1.87.0 (2025-05-06) 2. 安装 Rust 2.1 使用 Rust 官方安…...

Mysql8 忘记密码重置,以及问题解决
1.使用免密登录 找到配置MySQL文件,我的文件路径是/etc/mysql/my.cnf,有的人的是/etc/mysql/mysql.cnf 在里最后加入 skip-grant-tables重启MySQL服务 service mysql restartShutting down MySQL… SUCCESS! Starting MySQL… SUCCESS! 重启成功 2.登…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...
