[保研/考研机试] KY212 二叉树遍历 华中科技大学复试上机题 C++实现
题目链接:
二叉树遍历_牛客题霸_牛客网二叉树的前序、中序、后序遍历的定义: 前序遍历:对任一子树,先访问根,然后遍历其左子树,最。题目来自【牛客题霸】https://www.nowcoder.com/share/jump/437195121692587727256
描述
二叉树的前序、中序、后序遍历的定义: 前序遍历:对任一子树,先访问根,然后遍历其左子树,最后遍历其右子树; 中序遍历:对任一子树,先遍历其左子树,然后访问根,最后遍历其右子树; 后序遍历:对任一子树,先遍历其左子树,然后遍历其右子树,最后访问根。 给定一棵二叉树的前序遍历和中序遍历,求其后序遍历(提示:给定前序遍历与中序遍历能够唯一确定后序遍历)。
输入描述:
两个字符串,其长度n均小于等于26。 第一行为前序遍历,第二行为中序遍历。 二叉树中的结点名称以大写字母表示:A,B,C....最多26个结点。
输出描述:
输入样例可能有多组,对于每组测试样例, 输出一行,为后序遍历的字符串。
示例1
输入:
ABC
BAC
FDXEAG
XDEFAG输出:
BCA
XEDGAF思路:
先来一个例子:
先序遍历序列为:FDXEAG
中序遍历序列为:XDEFAG
要根据先序序列和中序序列确定这个二叉树,通用的步骤为:
1.根据先序序列的第一位确定这棵树的根;
2.在中序序列中找到根的所在的位置,根的左边就是该树的左子树的节点,根的右边就是该树的右子树的节点;
3.根据树的左子树节点和右子树节点在先序序列中分别找到对应的子串;
4.对3中找到的两个子串分别重复1 2 3步,左子树节点用于构建左子树,右子树节点用于构建右子树,直到所有的节点都用于构建这棵树。
示例:
根据以上的案例走一遍:
1.由先序遍历序列为:FDXEAG可知,树的根节点为F;
2.在中序遍历序列XDEFAG找到F的索引为3,左边XDE就是该树的左子树的节点,右边AG就是该树的右子树的节点;
3.根据树的左子树节点XDE和右子树节点AG在先序序列中分别找到对应的子串,分别为:DXE和AG;
4.对DXE和AG分别重复步骤1 2 3,DXE用于构建左子树,AG用于构建右子树,直到所有的节点都用于构建树。
每执行完第一轮步骤1 2 3,所用的根节点已经用于构建树了,后续就不用再考虑了。例如,执行完第一轮步骤1 2 3,根节点F已经用过了,后续就不用再考虑了。
分析:
相信思路都很明确,步骤大概也明白了,接下来代码实现中一个非常注重细节的地方就是递归构建左子树和右子树的部分,再详细说就是在递归调用构建树的函数中,我们要传入的两个参数应该怎么确定。
本次主要介绍利用先序遍历序列和中序遍历构建一个二叉树并输出后序遍历的方法,我们在递归调用构建树的函数中,我们要传入的两个参数当然就是子树的先序遍历序列和中序遍历序列。创建左子树时就传入左子树的先序遍历序列和中序遍历序列,创建右子树时就传入右子树的先序遍历序列和中序遍历序列。
以下根据以上案例详细分析:对于:
索 引:012345
先序遍历序列为:FDXEAG中序遍历序列为:XDEFAG将以上两个遍历序列分别命名为字符串s1,s2,即s1 = "FDXEAG", s2 = "XDEFAG"。根据s1可知树的根为F,在s2中寻找到F的索引(定义为pos)为3。根据s2可得左子树包括的字符有:XDE(由s2.substr(0, pos)获得),右子树包括的字符有:AG(由s2.substr(pos+1)获得),在s1中对应的字符串分别为:DXE(由s1.substr(1, pos)获得)和AG(由s1.substr(pos+1)获得)。根据以上获得的四个参数,可以递归创建左子树和右子树。
源代码:
//根据先序遍历和中序遍历确定一个二叉树
// 二叉树节点结构定义
struct TreeNode {char data;TreeNode* leftChild;TreeNode* rightChild;TreeNode(char c): data(c), leftChild(NULL), rightChild(NULL){}
};// 根据先序遍历和中序遍历构建二叉树
TreeNode* Build(string str1, string str2) {if (str1.size() == 0) {return NULL;}// 取先序遍历的第一个字符作为根节点char c = str1[0];// 在中序遍历中找到根节点的位置int pos = str2.find(c);// 创建根节点TreeNode* root = new TreeNode(c);递归构建左子树root->leftChild = Build(str1.substr(1, pos), str2.substr(0, pos));递归构建右子树root->rightChild = Build(str1.substr(pos + 1), str2.substr(pos + 1));return root;
}// 后序遍历输出
void postOrder(TreeNode* root) {if (root == NULL) {return;}//先遍历左子树postOrder(root->leftChild);//再遍历右子树postOrder(root->rightChild);//输出当前根节点的值cout << root->data;return;
}int main()
{string s1, s2;while (getline(cin, s1)) {getline(cin, s2);TreeNode* root = Build(s1, s2);postOrder(root);cout << endl;}return 0;
}
示例运行结果:
相关文章:

[保研/考研机试] KY212 二叉树遍历 华中科技大学复试上机题 C++实现
题目链接: 二叉树遍历_牛客题霸_牛客网二叉树的前序、中序、后序遍历的定义: 前序遍历:对任一子树,先访问根,然后遍历其左子树,最。题目来自【牛客题霸】https://www.nowcoder.com/share/jump/43719512169…...
CSS笔记
介绍 CSS导入方式 三种方法都将文字设置成了红色 CSS选择器 元素选择器 id选择器 图中div将颜色控制为红色,#name将颜色控制为蓝色,谁控制的范围最小,谁就生效,所以第二个div是蓝色的。id属性值要唯一,否则报错。 clas…...

链栈Link-Stack
0、节点结构体定义 typedef struct SNode{int data;struct SNode *next; } SNode, *LinkStack; 1、初始化 bool InitStack(LinkStack &S) //S为栈顶指针(存数据的头节点) {S NULL;return true; } 2、入栈 bool Push(LinkStack &S, int e) {…...

Ubuntu 20系统WIFI设置静态IP地址,以及断连问题
最近工作需要购置了一台GPU机器,然后搭建了深度学习的运行环境,在工作中将这台机器当做深度学习的服务器来使用,前期已经配置好多用户以及基础环境。但最近通过xshell连接总是不间断的出现断连现象。 补充一点,Ubuntu系统中与网…...
(一)idea连接GitHub的全部流程(注册GitHub、idea集成GitHub、增加合作伙伴、跨团队合作、分支操作)
(二)Git在公司中团队内合作和跨团队合作和分支操作的全部流程(一篇就够)https://blog.csdn.net/m0_65992672/article/details/132336481 4.1、简介 Git是一个免费的、开源的*分布式**版本控制**系统*,可以快速高效地…...

-bash: java: command not found笔记
文章目录 场景解决方案找java的方法find命令进行查找根据java进程找寻具体位置 场景 linux系统执行java命令时报错: -bash: java: command not found。 解决方案 可能是没有安装java(这种情况比较少)或者安装了java但是没有设置环境变量(一般是这种情况)。 找ja…...

C++ typename and .template
https://makecleanandmake.com/2015/07/20/leading-typename-dot-template-and-why-they-are-necessary/ typename Obj<T>::type var;v.template m<int>();...
uniapp,使用canvas制作一个签名版
先看效果图 我把这个做成了页面,没有做成组件,因为之前我是配合uview-plus的popup弹出层使用的,这种组件好像是没有生命周期的,第一次打开弹出层可以正常写字,但是关闭之后再打开就不会显示绘制的线条了,还…...

【大数据】Flink 详解(五):核心篇 Ⅳ
Flink 详解(五):核心篇 Ⅳ 45、Flink 广播机制了解吗? 从图中可以理解 广播 就是一个公共的共享变量,广播变量存于 TaskManager 的内存中,所以广播变量不应该太大,将一个数据集广播后࿰…...

设计模式-建造者模式
核心思想 抽取共同的行为,允许使用者指定复杂对象的类型和内容,不需要了解内部的构建细节使用多个简单的行为构建一个复杂的对象,将对象的构建过程和它的表示分离,同样的构建过程可以创建不同的表示 优缺点 优点 使用者不需要知…...

flutter 设置app图标
使用插件 flutter_launcher_icons 在 pubspec.yaml 配置文件中 加入 dev_dependencies dev_dependencies: flutter_launcher_icons: "^0.13.1" 准备好app得 icon 图标 其中icon的名字为icon.png 创建assets文件夹 和子文件夹icon iamge 配置静态资源路径 完整配置…...

守护网络安全:深入了解DDOS攻击防护手段
ddos攻击防护手段有哪些?在数字化快速发展的时代,网络安全问题日益凸显,其中分布式拒绝服务(DDOS)攻击尤为引人关注。这种攻击通过向目标网站或服务器发送大量合法或非法的请求,旨在使目标资源无法正常处理其他用户的请求,从而达…...
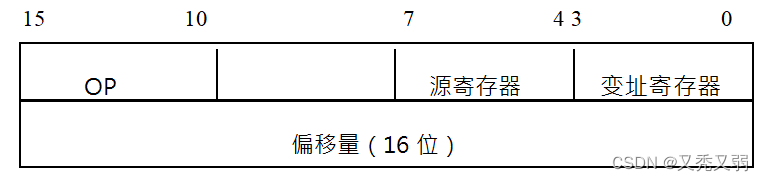
计组 | 寻址方式
目录 一、知识点 1.寻址方式什么? 2.根据操作数所在的位置,都有哪些寻址方式? 3.直接寻址 4.立即寻址 5.隐含寻址 6.相对寻址 7.寄存器 8.寄存器-寄存器型(RR)、寄存器-存储器型(RS)和…...

matlab工具箱Filter Designer设计butterworth带通滤波器
1、在matlab控制界面输入fdatool; 2、在显示的界面中选择合适的参数;本实验中采样频率是200,低通30hz,高通60hz,点击butterworth滤波器。 3、点击设计滤波器按钮后,在生成的界面点击红框按钮,可生成simulink模型到当前…...
)
Python学习笔记第六十天(Matplotlib Pyplot)
Python学习笔记第六十天 Matplotlib Pyplot后记 Matplotlib Pyplot Pyplot 是 Matplotlib 的子库,提供了和 MATLAB 类似的绘图 API。 Pyplot 是常用的绘图模块,能很方便让用户绘制 2D 图表。 Pyplot 包含一系列绘图函数的相关函数,每个函数…...

服务器自动备份、打包、传输脚本
备份脚本 #!/bin/bash #author cheng #备份服务器自动打包归档每天的备份文件 Path/backhistory Host$(hostname) Date$(date %F) Dest${Host}_${Date}#创建目录 mkdir -p ${Path}/${Dest}#打包文件到目录 cd / && \#结合autoback.sh脚本,它往那个地方备&a…...

Docker 的数据管理 网络通信
目录 1.管理容器数据的方式 数据卷 数据卷的容器 2.操作命令 3.Docker 镜像的创建 1.管理容器数据的方式 数据卷 可以独立于容器生命周期存储的机制 可提供持久化 数据共享 docker run -v /var/www:/data1 --name web1 -it centos:7 /bin/bash 数据卷的容器 用来提供持久化数…...

目标检测YOLO实战应用案例100讲-基于孤立森林算法的高光谱遥感图像异常目标检测
目录 前言 孤立森林算法的基本理论 2.1 引言 2.2 孤立森林算法的基本思想...
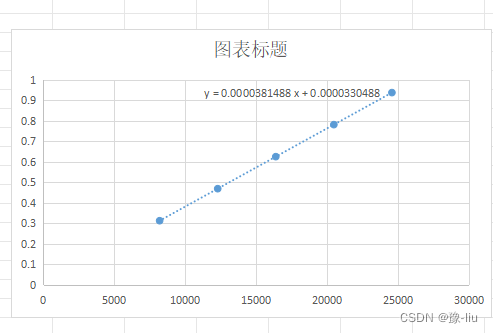
excel中两列数据生成折线图
WPS中excel的两列数据,第一列为x轴,第二列为y轴,生成折线图,并生成拟合函数。 1.选中两列数据,右击选择插入图表,选择XY(散点图),生成散点折线图 2.选中图中散点&#x…...
JS加密的域名锁定功能,JShaman支持泛域名
JShaman的域名锁定功能,支持泛域名 JShaman的JS代码混淆加密中,有一项“域名锁定”功能。使用此功能后,代码运行时会检测浏览器地址中的域名信息,如是非指定域名,则不运行,以此防止自己网站的JS代码被复制…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

比较数据迁移后MySQL数据库和OceanBase数据仓库中的表
设计一个MySQL数据库和OceanBase数据仓库的表数据比较的详细程序流程,两张表是相同的结构,都有整型主键id字段,需要每次从数据库分批取得2000条数据,用于比较,比较操作的同时可以再取2000条数据,等上一次比较完成之后,开始比较,直到比较完所有的数据。比较操作需要比较…...

MinIO Docker 部署:仅开放一个端口
MinIO Docker 部署:仅开放一个端口 在实际的服务器部署中,出于安全和管理的考虑,我们可能只能开放一个端口。MinIO 是一个高性能的对象存储服务,支持 Docker 部署,但默认情况下它需要两个端口:一个是 API 端口(用于存储和访问数据),另一个是控制台端口(用于管理界面…...

sshd代码修改banner
sshd服务连接之后会收到字符串: SSH-2.0-OpenSSH_9.5 容易被hacker识别此服务为sshd服务。 是否可以通过修改此banner达到让人无法识别此服务的目的呢? 不能。因为这是写的SSH的协议中的。 也就是协议规定了banner必须这么写。 SSH- 开头,…...

在golang中如何将已安装的依赖降级处理,比如:将 go-ansible/v2@v2.2.0 更换为 go-ansible/@v1.1.7
在 Go 项目中降级 go-ansible 从 v2.2.0 到 v1.1.7 具体步骤: 第一步: 修改 go.mod 文件 // 原 v2 版本声明 require github.com/apenella/go-ansible/v2 v2.2.0 替换为: // 改为 v…...

Java多线程实现之Runnable接口深度解析
Java多线程实现之Runnable接口深度解析 一、Runnable接口概述1.1 接口定义1.2 与Thread类的关系1.3 使用Runnable接口的优势 二、Runnable接口的基本实现方式2.1 传统方式实现Runnable接口2.2 使用匿名内部类实现Runnable接口2.3 使用Lambda表达式实现Runnable接口 三、Runnabl…...
