【算法系列篇】二分查找——这还是你所知道的二分查找算法吗?

文章目录
- 前言
- 什么是二分查找算法
- 1.二分查找
- 1.1 题目要求
- 1.2 做题思路
- 1.3 Java代码实现
- 2.在排序数组中查找元素的第一个和最后一个位置
- 2.1 题目要求
- 2.2 做题思路
- 2.3 Java代码实现
- 3.搜索插入位置
- 3.1 题目要求
- 3.2 做题思路
- 3.3 Java代码实现
- 4.x的平方根
- 4.1 题目要求
- 4.2 做题思路
- 4.3 Java代码实现
- 5.山脉数组的峰顶索引
- 5.1 题目要求
- 5.2 做题思路
- 5.3 Java代码实现
- 6.寻找峰值
- 6.1 题目要求
- 6.3 做题思路
- 6.4 Java代码实现
- 7.寻找旋转数组中的最小值
- 7.1 题目要求
- 7.2 做题思路
- 7.3 Java代码实现
- 总结
前言
在生活中,我们往往会遇到在数组中查找某个确定的元素的时候,通常我们会选择使用暴力解法,这样虽然简单,但是时间复杂度是O(N),时间效率比较低。那么是否有方法可以使得在具有二段性的数组中找某一特定的元素的时间复杂度低于0(N)呢?答案是肯定的,当我们可以将数组分为两个部分的时候,也就是数组具有二段性的时候,可以使用二分查找的算法来进行高效的查找。通常二分查找的时间复杂度为O(logN)。那么这篇文章我将为大家分享关于二分查找的知识。
什么是二分查找算法
二分查找算法(Binary Search Algorithm)是一种在有序数组(但不仅限于有序数组)中查找特定元素的搜索算法。它采用分治策略,每次比较数组中间的元素,如果该元素等于目标值,则搜索结束,否则根据目标值与中间元素的大小关系,将搜索范围缩小为数组的左半部分或右半部分,然后在新的搜索范围内重复执行上述操作,直到找到目标值或确定目标值不存在于数组中。
二分查找算法的时间复杂度为O(log n),其中n为数组的长度。由于每次都能排除一半的元素,因此算法的效率非常高,尤其适用于大规模数据的查找操作。
其实二分查找算法本来并不难,只是实现二分查找算法时,需要注意一些细节,例如处理数组边界、处理相等的情况等。如果没有处理好边界和相等问题的时候,很容易造成死循环。
1.二分查找
https://leetcode.cn/problems/binary-search/
1.1 题目要求
给定一个 n 个元素有序的(升序)整型数组 nums 和一个目标值 target ,写一个函数搜索 nums 中的 target,如果目标值存在返回下标,否则返回 -1。
示例 1:
输入: nums = [-1,0,3,5,9,12], target = 9
输出: 4
解释: 9 出现在 nums 中并且下标为 4
示例 2:
输入: nums = [-1,0,3,5,9,12], target = 2
输出: -1
解释: 2 不存在 nums 中因此返回 -1
提示:
- 你可以假设 nums 中的所有元素是不重复的。
- n 将在 [1, 10000]之间。
- nums 的每个元素都将在 [-9999, 9999]之间。
class Solution {public int search(int[] nums, int target) {}
}
1.2 做题思路
因为这道题目给的数组是有序的,我们 定义两个变量 left 和 right 分别从数组的开头和末尾开始,求 left 和 right 和的平均值的下标 mid ,然后看 mid 下标所代表的值与 target 的关系,如果 nums[mid] > target ,则可以确定在 [mid,right] 之间没有我们要找的 target 值,所以直接将这一半的数据给“舍弃”,将 right 的值更改为 mid - 1;如果 nums[mid] < target,则说明在 [left,mid] 这一范围内,没有我们需要找的 target 值,将这一部分给“舍弃”,left 的值更新为 mid + 1;如果nums[mid] = target,则返回 mid 的下标。 当然,这只是一种确定区间的方法,也可简单的称为“左闭右闭”,还有“左闭右开"、“左开右闭”这两种确定区间的方法,这两种方法是差不多的,那么就以“左闭右开”这种方式为大家介绍一下。我们前面为大家说明的是“左闭右闭”这种确定区间的方式,左闭右闭是指:left 和 right 这两个值,我们都可以取到,而左闭右开或者左开右闭则只是 left 或者 right 的数据可以取到。确定区间的方式不同,我们最终的循环条件也不同,究竟是 left < right,还是 left <= right,这就取决于我们区间的确定方式,如果是以“左闭右闭”的方式确定的,则需要加上等号,另外两种方式则不需要。 为什么呢?大家可以看看下面的图。
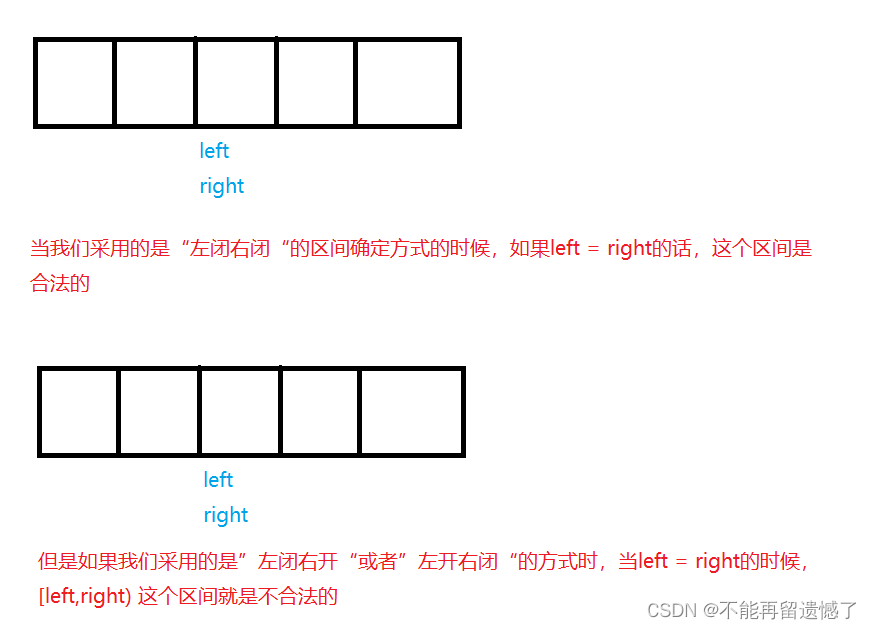
我们就以上面所讲的基本的二分查找算法来看看这道题目该怎么做。
1.3 Java代码实现
class Solution {//这里使用的”左闭右闭“的区间确定方式public int search(int[] nums, int target) {int left = 0;int right = nums.length-1;while(left <= right) {int mid = left + (right - left) / 2;if(nums[mid] < target) {left = mid + 1;}else if(nums[mid] > target) {right = mid - 1;}else {return mid;}}return -1;}
}
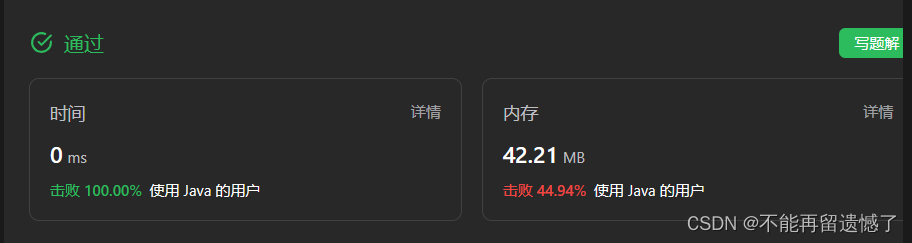
求 mid 的方式有两种,一种是 left + (right - left) / 2,一种是 left + (right - left + 1) / 2,这两种求 mid 的方式在这道题目是没什么区别的,具体的区别在后面的题目会遇到。
但是为什么我们不直接用 mid = (right - left) / 2 呢?因为我们不知道数组的大小为多少,很可能会造成 int 或者 long 类型不能够存储 left + right的值。
2.在排序数组中查找元素的第一个和最后一个位置
https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/
2.1 题目要求
给你一个按照非递减顺序排列的整数数组 nums,和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。
如果数组中不存在目标值 target,返回 [-1, -1]。
你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [5,7,7,8,8,10], target = 8
输出:[3,4]
示例 2:
输入:nums = [5,7,7,8,8,10], target = 6
输出:[-1,-1]
示例 3:
输入:nums = [], target = 0
输出:[-1,-1]
提示:
- 0 <= nums.length <= 105
- -109 <= nums[i] <= 109
- nums 是一个非递减数组
- -109 <= target <= 109
class Solution {public int[] searchRange(int[] nums, int target) {}
}
2.2 做题思路
做这道题目,如果使用和上面一样的思想的话,时间复杂度会降到 O(N),为什么呢?因为当你找到目标值之后,你还需要找到这个数的起始位置和结束位置,假设我们想要找的数是3,而数组中的数字全是3的话,那么就需要遍历整个数组一遍,时间复杂度就会降到 O(N),所以我们也就不能使用跟上面一样的思路,也就是朴素二分法,这道题需要我们使用到非朴素的二分算法,朴素算法其实是将数组分成了三个部分,小于目标值的部分,等于目标值的部分和大于目标值的部分,而非朴素算法则是真正的将数组分成了两个部分:小于等于目标值的部分和大于目标值的部分或者是小于目标值的部分和大于等于目标值的部分。这道题就是非朴素算法的思路,将数组分为了两个部分。
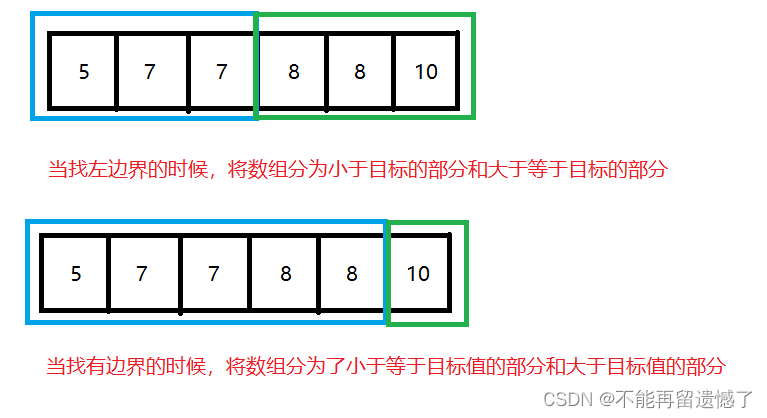
寻找左边界的时候,如果 nums[mid] < target ,则说明 mid 在小于目标值的那一部分,这部分肯定没有我们需要的数字,所以将 left 改为 mid + 1,而如果
numd[mid] >= target 的时候,就不能将 right 改为 mid - 1了,因为这个 mid 值可能刚好是我们需要找的值,所以将 right 的值改为 mid 而不是 mid - 1
在寻找有边界的时候,数组被分为了小于等于和大于目标值的两部分,当
nums[mid] <= target 的时候,因为 mid 所指向的位置可能是我们要找的值,所以 left = mid,当 nums[mid] > target 的值,因为在 [mid,righ] 之间肯定没有我们想要找的值,所以right = mid - 1.
数组分为不同的两部分,求 mid 的方法也是不同的,这也就是上面说的 mid = left + (right - left) / 2 和 mid = left + (right - left + 1) / 2的区别。
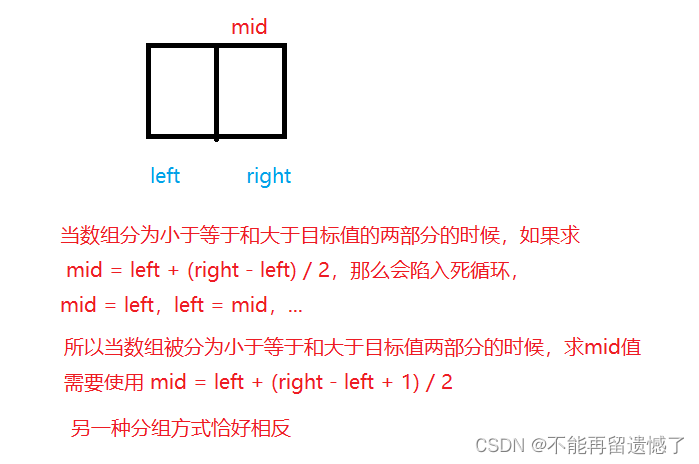
注意了,循环条件一定不能加等号,因为当left = right的时候,这个相遇的值恰好是我们需要的值,所以没必要多判断一次,更重要的是会陷入死循环。

2.3 Java代码实现
class Solution {public int[] searchRange(int[] nums, int target) {int[] ret = new int[]{-1,-1};int n = nums.length;if(n == 0) return ret; //当数组大小为0时,直接返回int left = 0;int right = n - 1;//求目标值的第一个位置while(left < right) {int mid = left + (right - left) / 2;if(nums[mid] < target) {left = mid + 1;}else {right = mid;}}if(nums[left] == target) ret[0] = left; //判断数字中是否存在目标值right = n - 1;//求目标值的最后一个位置while(left < right) {int mid = left + (right - left + 1) / 2;if(nums[mid] > target) {right = mid - 1;}else {left = mid;}}if(nums[left] == target) ret[1] = left;return ret;}
}
3.搜索插入位置
https://leetcode.cn/problems/search-insert-position/
3.1 题目要求
给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。
请必须使用时间复杂度为 O(log n) 的算法。
示例 1:
输入: nums = [1,3,5,6], target = 5
输出: 2
示例 2:
输入: nums = [1,3,5,6], target = 2
输出: 1
示例 3:
输入: nums = [1,3,5,6], target = 7
输出: 4
提示:
- 1 <= nums.length <= 104
- -104 <= nums[i] <= 104
- nums 为 无重复元素 的 升序 排列数组
- -104 <= target <= 104
class Solution {public int searchInsert(int[] nums, int target) {}
}
3.2 做题思路
根据题目,我们可以知道,这个题目大致分为两种情况:目标值在数组中,返回目标值的下标,如果目标值不存在则返回目标值应该插入位置的下标。
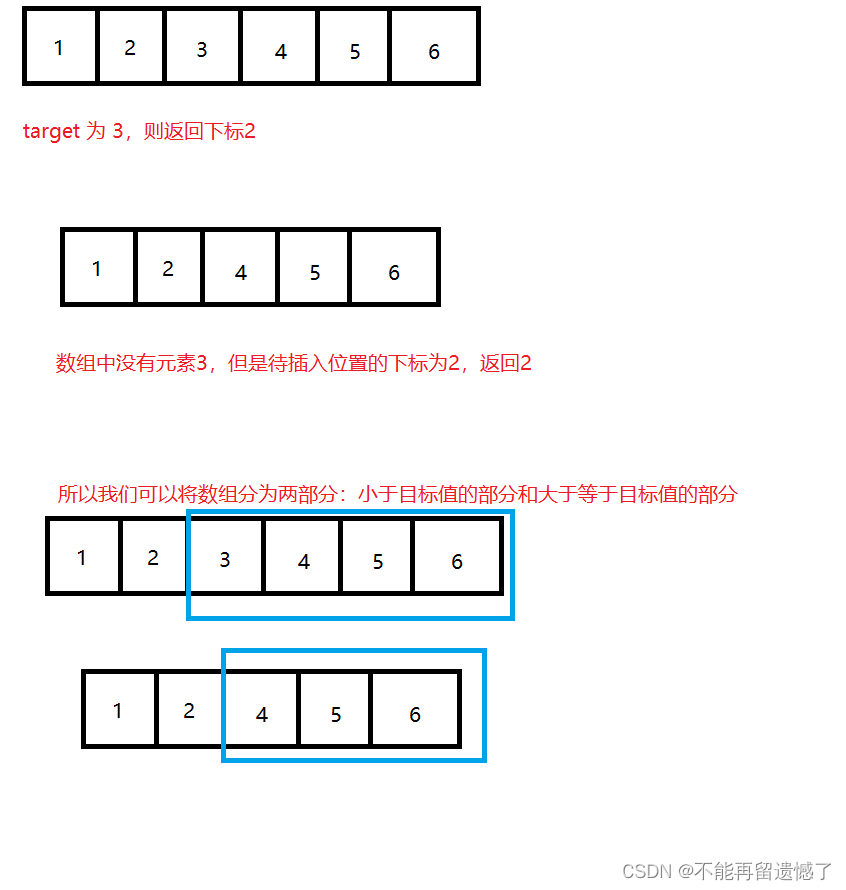
可以将数组分为两个部分,这就可以用到我们的二分查找算法了。
3.3 Java代码实现
class Solution {public int searchInsert(int[] nums, int target) {int n = nums.length;int left = 0;int right = n - 1;while(left < right) {int mid = left + (right - left) / 2;if(nums[mid] < target) {left = mid + 1;}else {right = mid;}}if(nums[left] < target) return left + 1; //当待插入位置位于数组的末尾时,需要作出判断else return left;}
}
4.x的平方根
https://leetcode.cn/problems/sqrtx/
4.1 题目要求
给你一个非负整数 x ,计算并返回 x 的 算术平方根 。
由于返回类型是整数,结果只保留 整数部分 ,小数部分将被 舍去 。
注意:不允许使用任何内置指数函数和算符,例如 pow(x, 0.5) 或者 x ** 0.5 。
示例 1:
输入:x = 4
输出:2
示例 2:
输入:x = 8
输出:2
解释:8 的算术平方根是 2.82842..., 由于返回类型是整数,小数部分将被舍去。
提示:
- 0 <= x <= 231 - 1
class Solution {public int mySqrt(int x) {}
}
4.2 做题思路
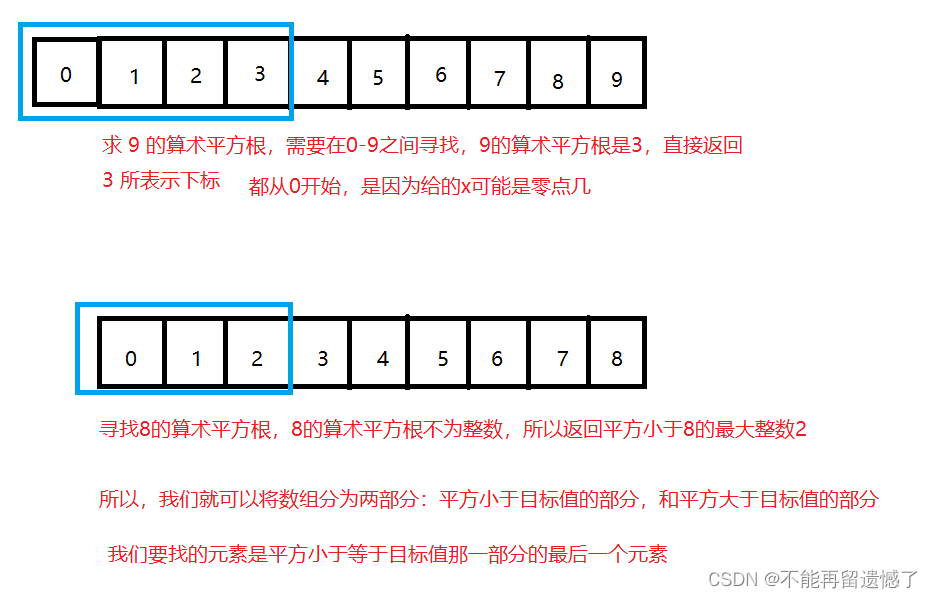
如果 x 的平方根为整数的话,则直接返回,如果不是整数的话,则返回平方小于 x 的最大整数,通过这样理解题目,我们也可以将数组分为两个部分,小于等于 x 的部分和大于 x 的部分。同样,使用二分查找的算法解决。
4.3 Java代码实现
class Solution {public int mySqrt(int x) {long left = 0; //这里mid * mid可能会很大,超出 int 所能表示的范围,所以我们用 long 来表示long right = x;while(left < right) {long mid = left + (right - left + 1) / 2;if(mid * mid > x) {right = mid - 1;}else {left = mid;}}return (int)left;}
}
5.山脉数组的峰顶索引
https://leetcode.cn/problems/peak-index-in-a-mountain-array/
5.1 题目要求
符合下列属性的数组 arr 称为 山脉数组 :
- arr.length >= 3
- 存在 i(0 < i < arr.length - 1)使得:
-
- arr[0] < arr[1] < … arr[i-1] < arr[i]
-
- arr[i] > arr[i+1] > … > arr[arr.length - 1]
给你由整数组成的山脉数组 arr ,返回满足 arr[0] < arr[1] < … arr[i - 1] < arr[i] > arr[i + 1] > … > arr[arr.length - 1] 的下标 i 。
- arr[i] > arr[i+1] > … > arr[arr.length - 1]
你必须设计并实现时间复杂度为 O(log(n)) 的解决方案。
示例 1:
输入:arr = [0,1,0]
输出:1
示例 2:
输入:arr = [0,2,1,0]
输出:1
示例 3:
输入:arr = [0,10,5,2]
输出:1
提示:
- 3 <= arr.length <= 105
- 0 <= arr[i] <= 106
- 题目数据保证 arr 是一个山脉数组
class Solution {public int peakIndexInMountainArray(int[] arr) {}
}
5.2 做题思路
因为题目保证数组 arr 是一个山脉数组,有很明显的二段性,所以很容易想到二分查找的算法。
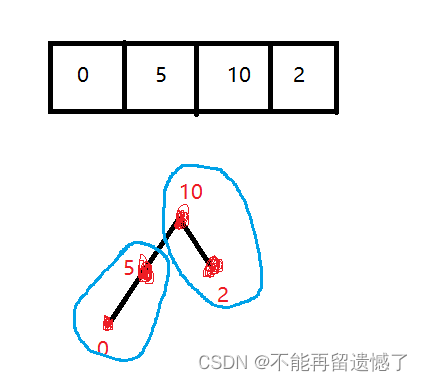
将数组分为两部分:小于峰顶值的部分和大于等于峰顶值的部分。当 mid 落在小于峰顶值的部分时,我们使 left = mid + 1,如果 mid 落在 大于等于峰顶值的部分时,令right = mid。
5.3 Java代码实现
class Solution {public int peakIndexInMountainArray(int[] arr) {int left = 0;int right = arr.length - 1;while(left < right) {int mid = left + (right - left) / 2;if(arr[mid] < arr[mid + 1]) {left = mid + 1;}else {right = mid;}}return left;}
}
6.寻找峰值
https://leetcode.cn/problems/find-peak-element/
6.1 题目要求
峰值元素是指其值严格大于左右相邻值的元素。
给你一个整数数组 nums,找到峰值元素并返回其索引。数组可能包含多个峰值,在这种情况下,返回 任何一个峰值 所在位置即可。
你可以假设 nums[-1] = nums[n] = -∞ 。
你必须实现时间复杂度为 O(log n) 的算法来解决此问题。
示例 1:
输入:nums = [1,2,3,1]
输出:2
解释:3 是峰值元素,你的函数应该返回其索引 2。
示例 2:
输入:nums = [1,2,1,3,5,6,4]
输出:1 或 5
解释:你的函数可以返回索引 1,其峰值元素为 2;或者返回索引 5, 其峰值元素为 6。
提示:
- 1 <= nums.length <= 1000
- -231 <= nums[i] <= 231 - 1
- 对于所有有效的 i 都有 nums[i] != nums[i + 1]
class Solution {public int findPeakElement(int[] nums) {}
}
6.3 做题思路
注意看题目,题目中给了,可以假设 nums[-1] = nums[n] = 负无穷,所以可以将数组看成是从负无穷加到一个峰值,然后再从峰值减小到负无穷,即使你数组中的元素是单调的,也会形成山峰的形状,很明显的二段性,所以使用二分查找的算法。同样将数组分为两部分:小于峰值的部分和大于等于峰值的部分。
6.4 Java代码实现
class Solution {public int findPeakElement(int[] nums) {int left = 0;int right = nums.length - 1;while(left < right) {int mid = left + (right - left) / 2;if(nums[mid] < nums[mid + 1]) {left = mid + 1;}else {right = mid;}}return left;}
}
7.寻找旋转数组中的最小值
https://leetcode.cn/problems/find-minimum-in-rotated-sorted-array/
7.1 题目要求
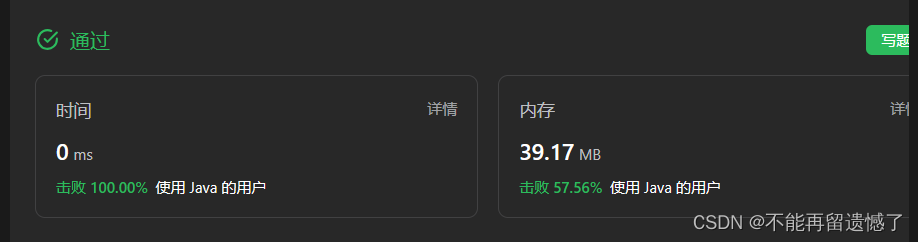
已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到:
- 若旋转 4 次,则可以得到 [4,5,6,7,0,1,2]
- 若旋转 7 次,则可以得到 [0,1,2,4,5,6,7]
注意,数组 [a[0], a[1], a[2], …, a[n-1]] 旋转一次 的结果为数组 [a[n-1], a[0], a[1], a[2], …, a[n-2]] 。
给你一个元素值 互不相同 的数组 nums ,它原来是一个升序排列的数组,并按上述情形进行了多次旋转。请你找出并返回数组中的 最小元素 。
你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。
示例 1:
输入:nums = [3,4,5,1,2]
输出:1
解释:原数组为 [1,2,3,4,5] ,旋转 3 次得到输入数组。
示例 2:
输入:nums = [4,5,6,7,0,1,2]
输出:0
解释:原数组为 [0,1,2,4,5,6,7] ,旋转 4 次得到输入数组。
示例 3:
输入:nums = [11,13,15,17]
输出:11
解释:原数组为 [11,13,15,17] ,旋转 4 次得到输入数组。
提示:
- n == nums.length
- 1 <= n <= 5000
- -5000 <= nums[i] <= 5000
- nums 中的所有整数 互不相同
- nums 原来是一个升序排序的数组,并进行了 1 至 n 次旋转
class Solution {public int findMin(int[] nums) {}
}
7.2 做题思路
无论数组旋转多少次,总会将前面部分的升序数组给旋转到后面部分数组的后面,通过画图我们可以看出,这又是明显的具有二段性的数组,可以使用二分查找的算法来解决。
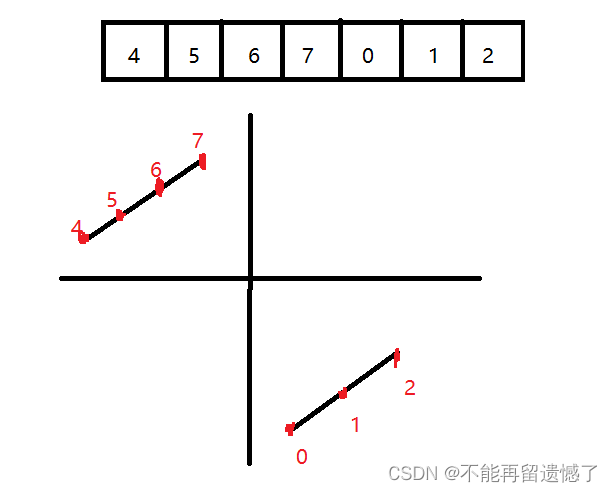
数组的两个部分中,较大的部分中的所有元素都大于较小数组部分的最大值,而我们要找的最小的值也就是在较小的那一部分中,所以我们将数组分为大于 nums[n-1] 的部分和小于等于nums[n-1] 两部分,当 mid 落在大于 nums[n-1] 的部分时,left = mid + 1,当 mid 落在小于等于 numd[n-1] 的部分时,right = mid。
7.3 Java代码实现
class Solution {public int findMin(int[] nums) {int n = nums.length;int left = 0;int right = n - 1;while(left < right) {int mid = left + (right - left) / 2;if(nums[mid] > nums[n-1]) {left = mid + 1;}else {right = mid;}}return nums[left];}
}
总结
其实二分查找这个算法不算难,只要主要好边界条件、区间,不造成死循环其实就很简单,只要知道了可以将数组分为哪两部分,就可以直接套模板,通过看上面几道题目的代码我们也可以看出,代码基本上类似,所以大家只要能够将数组分为两部分和不同部分区间的变化条件和区间的变化就可以了。
相关文章:

【算法系列篇】二分查找——这还是你所知道的二分查找算法吗?
文章目录 前言什么是二分查找算法1.二分查找1.1 题目要求1.2 做题思路1.3 Java代码实现 2.在排序数组中查找元素的第一个和最后一个位置2.1 题目要求2.2 做题思路2.3 Java代码实现 3.搜索插入位置3.1 题目要求3.2 做题思路3.3 Java代码实现 4.x的平方根4.1 题目要求4.2 做题思路…...

【前端从0开始】JavaSript——分支流程控制
流程控制 在任何一门程序设计语言中,都需要支持满足程序结构 化所需要的三种流程控制: ●顺序控制 ●分支控制(条件控制) ●循环控制 顺序控制:在程序流程控制中,最基本的就是顺序控制。程序会按照自上而下的顺序执行…...
Linux权限
Linux中一切皆文件,那么文件就应该有相对于的类型,而在Linux当中,类型不是直接看后缀来决定的。 -普通文件、文本、可执行、归档文件等d目录b块设备、block、磁盘c字符设备、键盘、显示器p管道文件s网络socket文件l链接文件 link 然后后面的九…...

PMP如何备考?学习方式这里有
预习阶段:强烈建议跟着习课视频学习(自己看书真的很难看懂),初步了解PMBOK,有个大致印象; 精讲阶段:这个时候就需要静下心来深入了解各个知识模块,不仅是看PMBOK,还要尽…...
【Java转Go】快速上手学习笔记(四)之基础篇三
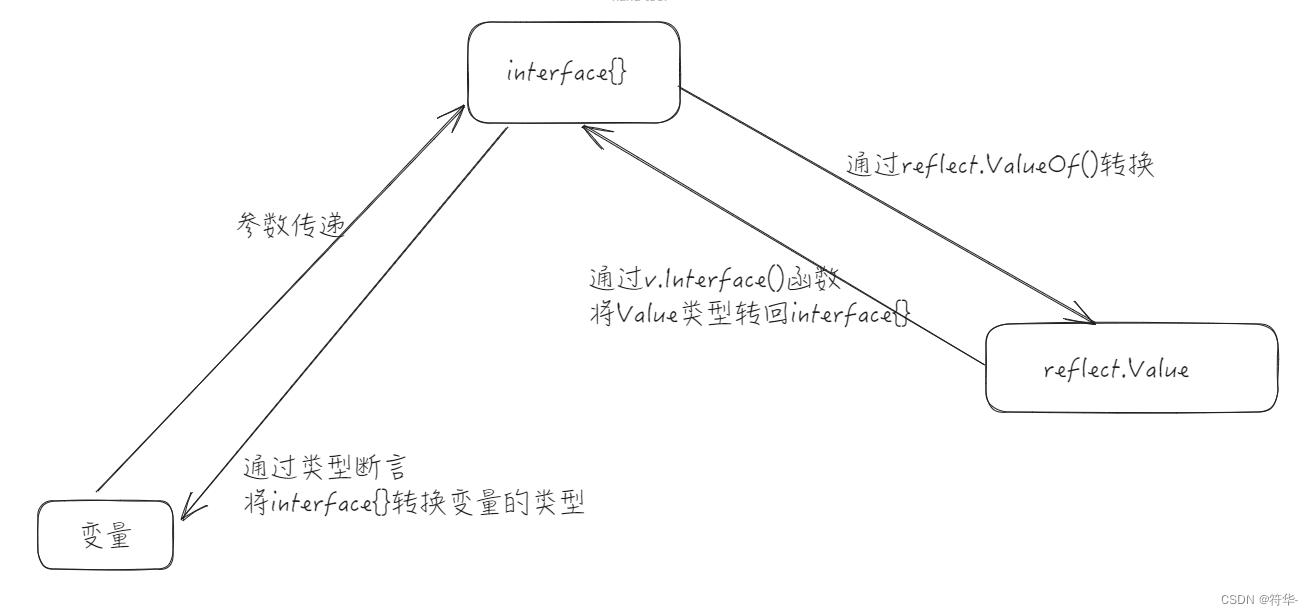
目录 泛型内置泛型的使用切片泛型和泛型函数map泛型泛型约束泛型完整代码 接口反射协程特点WaitGroupgoroutine的调度模型:MPG模型 channel介绍语法:举例:channel遍历基本使用和协程一起使用案例一案例二 select...casemain.go 完整代码 文件…...
vue中form和table标签过长
form标签过长 效果: 代码: <el-form-item v-for"(item,index) in ticketEditTable1" :label"item.fieldNameCn" :propitem.fieldName :key"item.fieldNameCn" overflow"":rules"form[item.fieldName…...
)
java基础复习(第七日)
java基础复习(七) 1.MQ如何避免消息重复投递或重复消费? 在消息生产时,MQ 内部针对每条生产者发送到消息生成一个 inner-msg-id,作为去重的依据(消息投递失败并重传),避免重复的消息进入队列;…...

day24 | 理论基础、77. 组合
目录: 解题及思路学习 理论基础 回溯的本质是穷举,穷举所有可能,然后选出我们想要的答案,如果想让回溯法高效一些,可以加一些剪枝的操作,但也改不了回溯法就是穷举的本质。 回溯法,一般可以…...
)
数据结构(1)
数据结构其实就是将数据按照一定的关系组织起来的集合,用于组织和存储数据。 1.数据结构分类 1.逻辑结构 逻辑结构是从具体问题中抽象出来的模型,是抽象意义的结构,按照对象中数据的相互关系进行分类。 1>集合结构:集合结构中…...

10个非常有用的Python库,你知道几个?
整理|TesterHome 这里给大家介绍10个不是最流行但非常有用的Python库,希望可以提供参考帮助。 PyO3 PyO3是一个Rust库,可以让你在Rust中编写Python模块。它可以利用 Rust 的速度和安全性编写高性能的 Python 模块。 https://github.com/PyO3…...
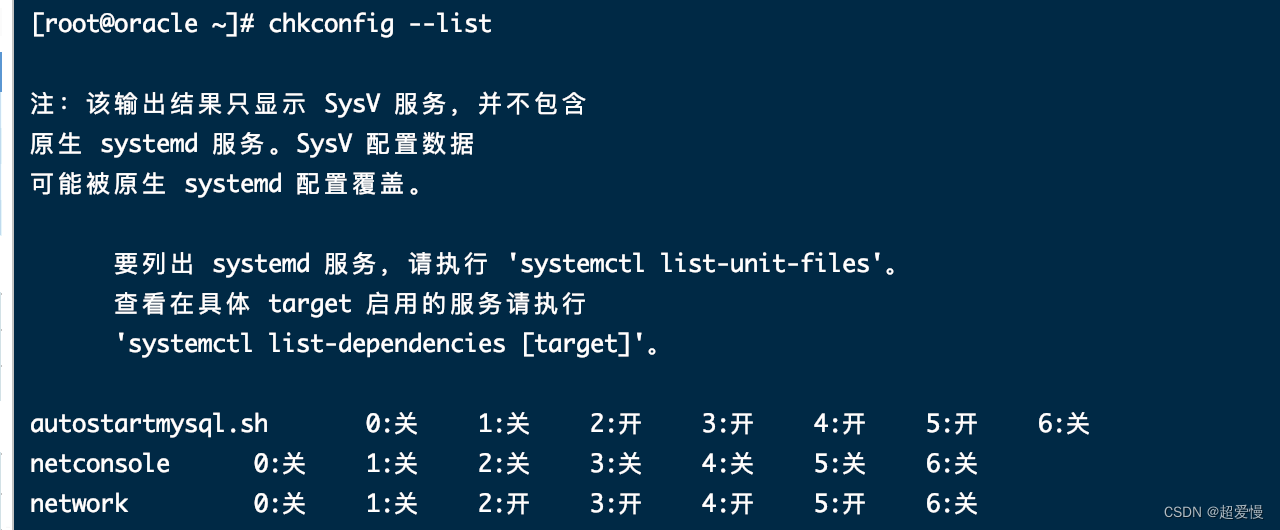
linux安装 MySQL8 并配置开机自启动
目录 1.下载 mysql 安装包 2.上传并解压 mysql 3.修改 mysql 文件夹名 4.创建mysql 用户和用户组 5.数据目录 (1)创建目录 (2)赋予权限 6.初始化mysql (1)配置参数 (2)配置环…...

MySQL视图
一、视图-介绍及基本语法 视图(View)是一种虚拟存在的表。视图中的数据并不在数据库中实际存在,行和列数据来自定义视图的查询中使用的表,并且是在使用视图时动态生成的。 通俗的讲,视图只保存了查询的SQL逻辑…...

Pytorch-day05-可视化-checkpoint
PyTorch 可视化 1、模型结构可视化2、训练过程可视化3、模型评估可视化 #导入常用包 import os import numpy as np import torch from torch import nn from torch.utils.data import Dataset, DataLoader from torchvision.transforms import transforms import torchvis…...

实训笔记8.23
8.23笔记 8.23笔记一、Hive中函数1.1 Hive中内置函数1.1.1 数学函数1.1.2 字符串函数1.1.3 日期函数1.1.4 条件函数1.1.5 特殊函数 1.2 Hive的自定义函数1.2.1 自定义UDF1.2.2 自定义UDTF 二、Hive的压缩机制三、数据同步工具Sqoop的安装和使用3.1 sqoop的概念3.2 sqoop的核心功…...

2023年菏泽市中职学校技能大赛“网络安全”赛项规程
2023年菏泽市中职学校技能大赛 “网络安全”赛项规程 一、赛项名称 赛项名称:网络安全 赛项所属专业大类:信息技术类 二、竞赛目的 通过竞赛,检验参赛选手对网络、服务器系统等网络空间中各个信息系统的安全防护能力,以及分析…...
Android 13 - Media框架(6)- NuPlayer
上一节我们通过 NuPlayerDriver 了解了 NuPlayer 的使用方式,这一节我们一起来学习 NuPlayer 的部分实现细节。 ps:之前用 NuPlayer 播放本地视频很多都无法播放,所以觉得它不太行,这两天重新阅读发现它的功能其实很全面ÿ…...

机器学习|DBSCAN 算法的数学原理及代码解析
机器学习|DBSCAN 算法的数学原理及代码解析 引言 聚类是机器学习领域中一项重要的任务,它可以将数据集中相似的样本归为一类。DBSCAN(Density-Based Spatial Clustering of Applications with Noise)是一种是一种经典的密度聚类…...
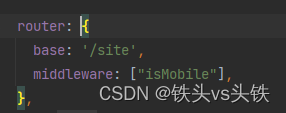
用NUXT.JS,轻松搞定SEO!
nuxt.js 是什么? 如果你正在准备开发一个SEO友好的新项目,而且准备用 vue 开发,那么恭喜你,用 nuxt 是一个成本和效率都比较优秀的方案。 官方文档 知识中心案例 简单介绍下背景,这是一个专门为氚云低代码平台引流…...

什么是电商RPA?电商RPA能解决什么问题?电商RPA实施难点在哪里?
RPA机器人可以应用于各个行业和领域,例如金融、保险、制造、物流、电商等。它可以减少人工错误和重复工作,提高效率和生产力。RPA还可以在处理大量数据时加快处理速度,提供更准确和可靠的结果。此外,RPA还可以为员工提供更有价值的…...

【BUG】Docker启动MySQL报错
个人主页:金鳞踏雨 个人简介:大家好,我是金鳞,一个初出茅庐的Java小白 目前状况:22届普通本科毕业生,几经波折了,现在任职于一家国内大型知名日化公司,从事Java开发工作 我的博客&am…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

算法:模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣(LeetCode) 遍历字符串:通过外层循环逐一检查每个字符。遇到 ? 时处理: 内层循环遍历小写字母(a 到 z)。对每个字母检查是否满足: 与…...

Java编程之桥接模式
定义 桥接模式(Bridge Pattern)属于结构型设计模式,它的核心意图是将抽象部分与实现部分分离,使它们可以独立地变化。这种模式通过组合关系来替代继承关系,从而降低了抽象和实现这两个可变维度之间的耦合度。 用例子…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...
