Electron环境搭建
Electron是一个优秀的开源框架,用于构建跨平台的桌面应用程序。它基于Chromium和Node.js,使得开发者可以使用Web技术(HTML、CSS和JavaScript)来构建可在Windows、macOS和Linux等多个操作系统上运行的应用程序。本文将介绍如何搭建Electron环境,快速开始您的桌面应用程序开发之旅。
第一步:安装Node.js和npm
Electron依赖于Node.js和npm(Node包管理器)。您需要首先安装Node.js,可以从其官方网站下载适合您操作系统的安装程序并进行安装。安装完成后,您可以在终端或命令提示符中输入以下命令来验证Node.js和npm是否成功安装:
node -v
npm -v
第二步:创建Electron项目
打开终端或命令提示符,进入您想要创建项目的目录,并执行以下命令来初始化Electron项目:
mkdir my-electron-app
cd my-electron-app
npm init
按照提示填写项目信息,完成初始化。
第三步:安装Electron
在项目目录下执行以下命令来安装Electron:
npm install electron --save-dev
此命令会将Electron作为开发依赖项进行安装,并自动将其添加到项目的package.json文件中。
第四步:创建主进程和渲染进程
在项目根目录下创建一个名为main.js的文件,用于编写主进程的代码。另外,创建一个名为index.html的文件,用于编写渲染进程的代码。您可以根据自己的需求进行开发和设计。
第五步:启动应用程序
在项目根目录下,通过以下命令启动您的Electron应用程序:
npx electron .
这将启动Electron并加载您编写的代码。您可以在Electron窗口中看到您的应用程序正在运行。
至此,您已成功搭建了Electron环境,并创建了一个简单的Electron应用程序。您可以根据需要继续开发和扩展,利用Electron丰富的API和功能,构建出功能强大的桌面应用程序。
希望本文对您有所帮助,祝您在Electron开发中取得成功!如有任何疑问,欢迎交流讨论。
结束语:
本文介绍了如何搭建Electron环境,并通过一个简单的示例来演示Electron应用程序的创建过程。通过运用Electron,开发者可以使用熟悉的前端技术来构建强大的跨平台桌面应用程序。希望该文章对您了解和入门Electron有所帮助。感谢阅读!
相关文章:

Electron环境搭建
Electron是一个优秀的开源框架,用于构建跨平台的桌面应用程序。它基于Chromium和Node.js,使得开发者可以使用Web技术(HTML、CSS和JavaScript)来构建可在Windows、macOS和Linux等多个操作系统上运行的应用程序。本文将介绍如何搭建…...
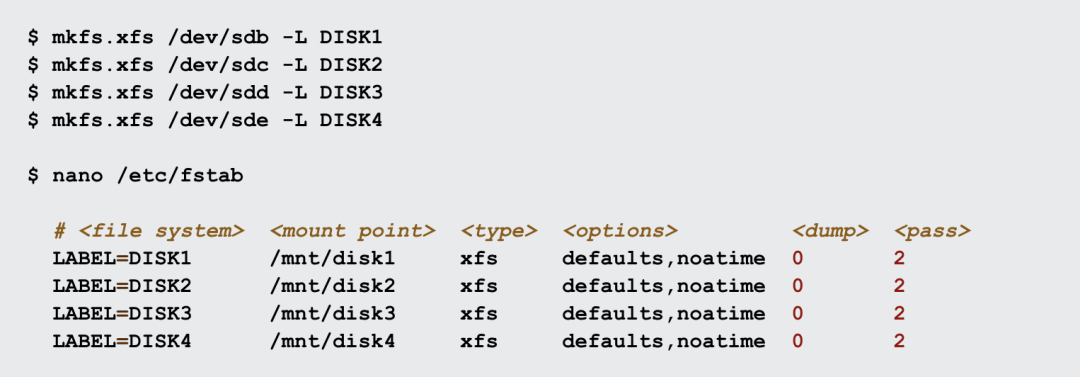
MinIO线上扩容实战
硬件投入肯定是随着业务的增长而增长,这就要求中间件平台必须提供水平伸缩机制,MinIO对象存储服务也不例外,本文就详细介绍MinIO的扩容。 Minio支持通过增加新的Server Pool来扩容老的集群。每个Server Pool都是一个相对独立的故障域&#x…...

【微服务】微服务的概论
微服务:构建面向为了解决这个问题,微服务架构应运而生。本文将向您介绍微服务的概念、优势、实现原理以及应用场景,带您领略微服务在构建面向未来的高效应用中的魅力。 一、微服务的概念和优势 微服务是一种将应用拆分为一系列小型、独立服…...
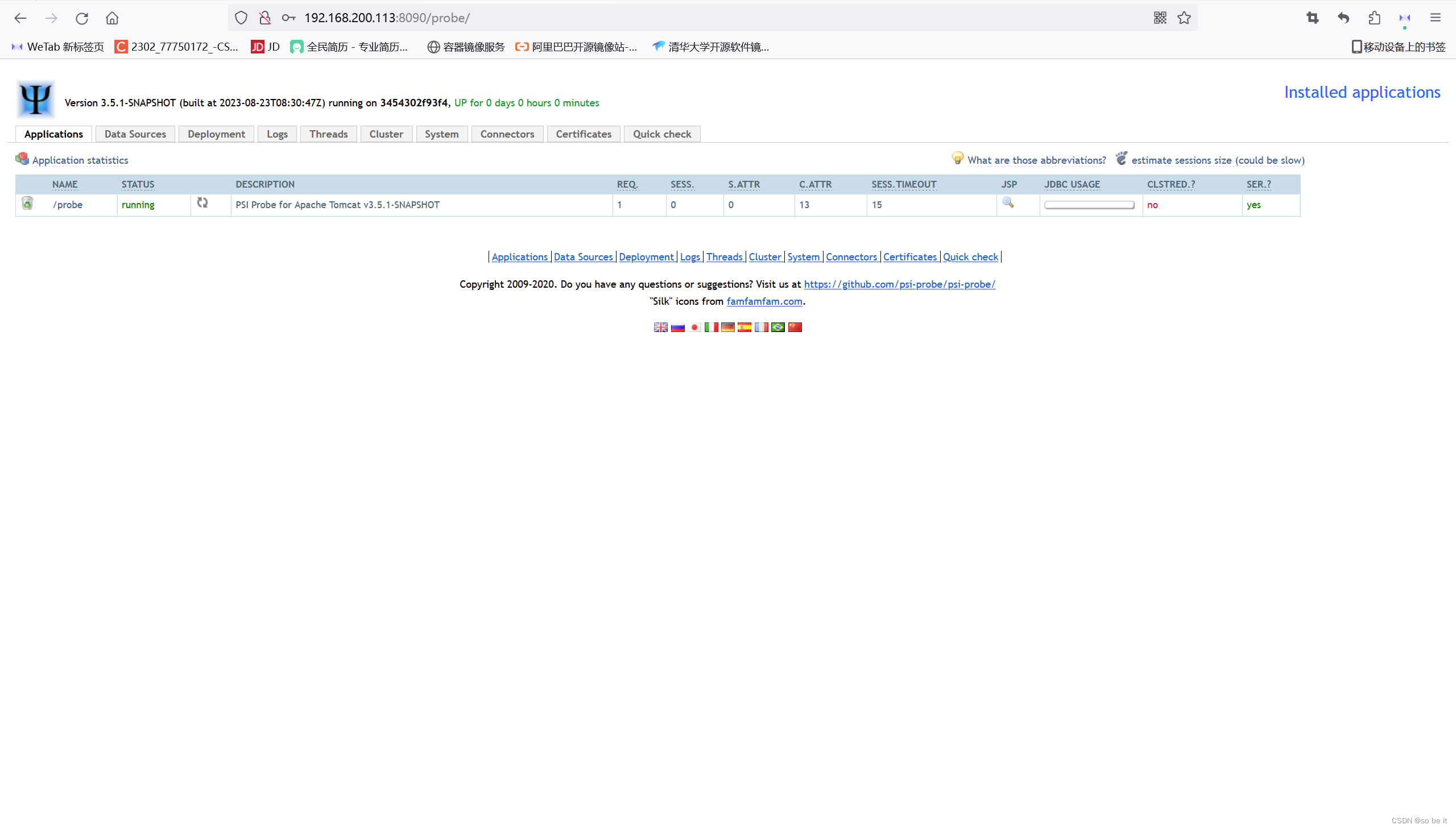
基于Jenkins自动打包并部署docker环境
目录 1、安装docker-ce 2、阿里云镜像加速器 3、构建tomcat 基础镜像 4、构建一个Maven项目 实验环境 操作系统 IP地址 主机名 角色 CentOS7.5 192.168.200.111 git git服务器 CentOS7.5 192.168.200.112 Jenkins git客户端 jenkins服务器 CentOS7.5 192.168…...

jvm 运行时数据区
Java虚拟机定义了若干种程序运行期间会使用到的运行时数据区,其中有一些会随着虚拟机启动而创建,随着虚拟机退出而销毁。另外一些则是与线程一一对应的,这些与线程对应的数据区域会随着线程开始和结束而创建和销毁 1.1程序计数器 程序计数器也叫pc寄存器 可以看作是当前线程…...
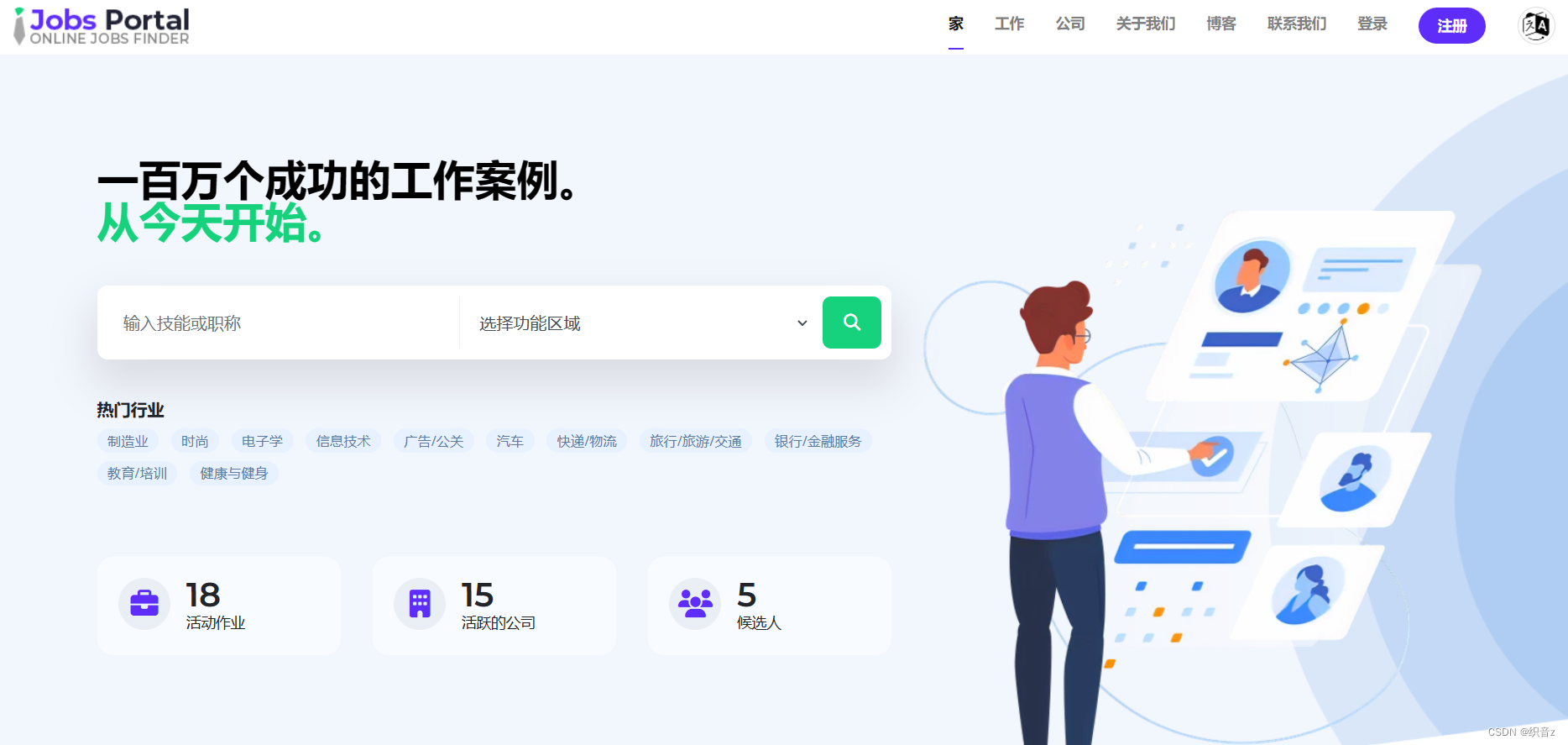
Jobs Portal求职招聘系统源码v3.5版本
Jobs Portal求职招聘系统 是为求职者和公司发布职位而开发的交互式求职招聘源码。它使求职者能够发布简历、搜索工作、查看个人工作列表。 它将提供各种公司在网站上放置他们的职位空缺资料,并且还可以选择搜索候选人简历。 除此之外,还有一个管理模块供…...
使用Intent在Activity之间穿梭)
Android kotlin系列讲解(入门篇)使用Intent在Activity之间穿梭
<<返回总目录 上一篇:Android kotlin系列讲解(入门篇)Activity的理解与基本用法 文章目录 1、使用显式Intent2、使用隐式Intent3、更多隐式Intent的用法4、向下一个Activity传递数据5、返回数据给上一个Activity1、使用显式Intent 你应该已经对创建Activity的流程比较…...

音频编码类型及对应的封装文件
音频编码类型及对应的封装文件 如下表格 编码类型解释文件封装audio/mp4a-latmMPEG-4 Audio Advanced Audio Coding (AAC) Low-Overhead Audio Transport Multiplex (LATM) 压缩的音频格式mp4audio/3gpp3rd Generation Partnership Project (3GPP) 定义的音频编码格式3GPaudi…...

初探科研 | 第一次科研经历
1 . 自己的experiences 自己大二下学期中比较幸运加入到科研组里,做的方向是3D人体姿态估计,不过由于是一个全新领域,基本也是自己这个小白探索,所以成果甚微。在八月初由于各种原因退出了组,但是在这期间收获还是蛮多…...
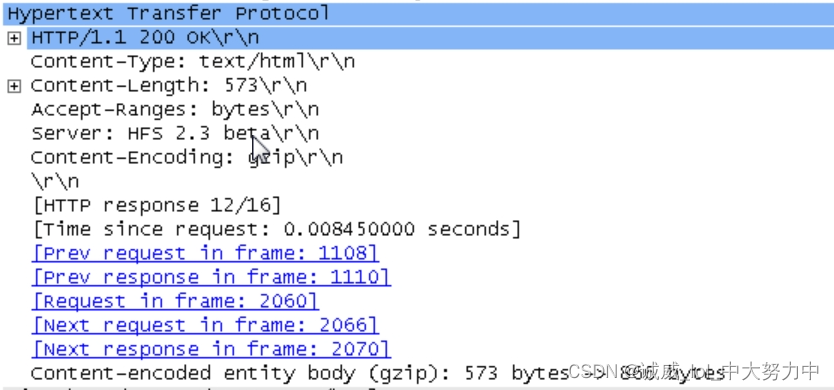
Wireshark数据抓包分析之HTTP协议
一、实验目的: 主要时熟悉wireshark的使用 二、预备知识: HTTP协议的相关知识 what fk,原来只要在右页点击切换,就可以开启2台不同的机器欸!nice 三、实验过程: 1.在机器1中通过管理员身份运行hfs之后&a…...
研发管理工具大揭秘!6款利器助你高效研发
"研发管理工具有哪些?6款研发管理利器分析Zoho Projects、Trello、Asana、Monday.com、Smartsheet、Jira。" 在如今的科技发展日新月异的时代,研发管理工具的重要性日益凸显。研发管理工具有助于提高研发效率,降低成本,…...

云知识入门-什么是虚拟机、磁盘、镜像和快照
一、虚拟机 1、什么是虚拟机 虚拟机(VM)是一种创建于物理硬件系统(位于外部或内部)、充当虚拟计算机系统的虚拟环境,它模拟出了自己的整套硬件,包括 CPU、内存、网络接口和存储器。通过名为虚拟机监控程序…...

C/C++编译整理
1. 编译器 查看编译情况 gcc main.c -o main -v # -v查看编译详情 g main.c -o main -v # -v查看编译详情添加预处理头文件 在PATH中找到可执行文件程序的路径 export PATH $PATH:$HOME/bin gcc找到头文件的路径 C_INCLUDE_PATH/usr/include/libxml2:/MyLib export C_I…...
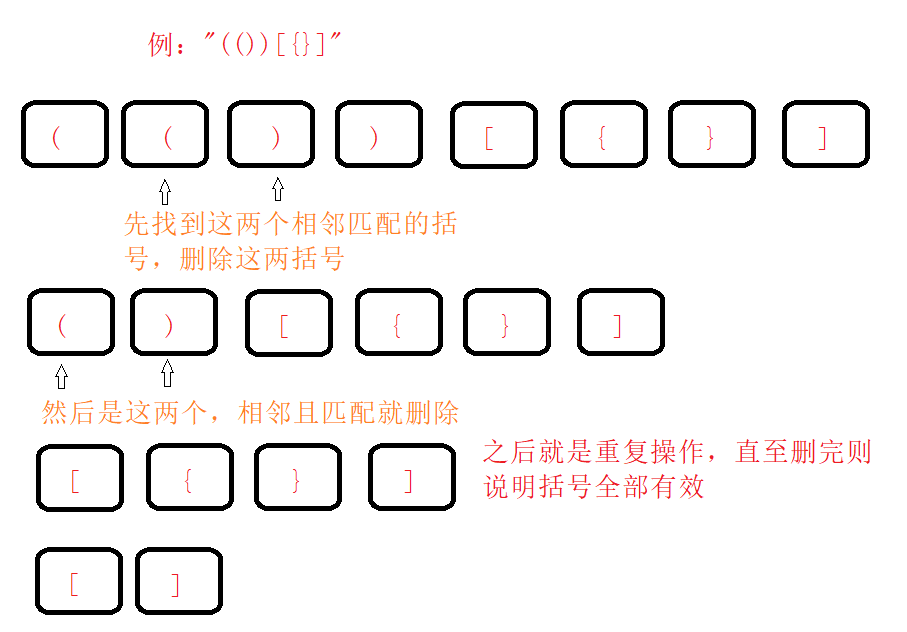
数据结构——栈和队列
栈和队列的建立 前言一、栈1.栈的概念2.栈的实现3.代码示例(1)Stack.h(2)Stack.c(3)Test.c(4)运行结果(5)完整代码演示 二、队列1.队列的概念2.队列的实现3.代…...

苍穹外卖阿里云oss存储笔记
阿里云oss 阿里云对象存储oss(Object Storage Service),是一款海量,安全,低成本,高可靠得云存储服务,使用oss,您可以通过网络随时存储和调用包括文本,图片,视…...
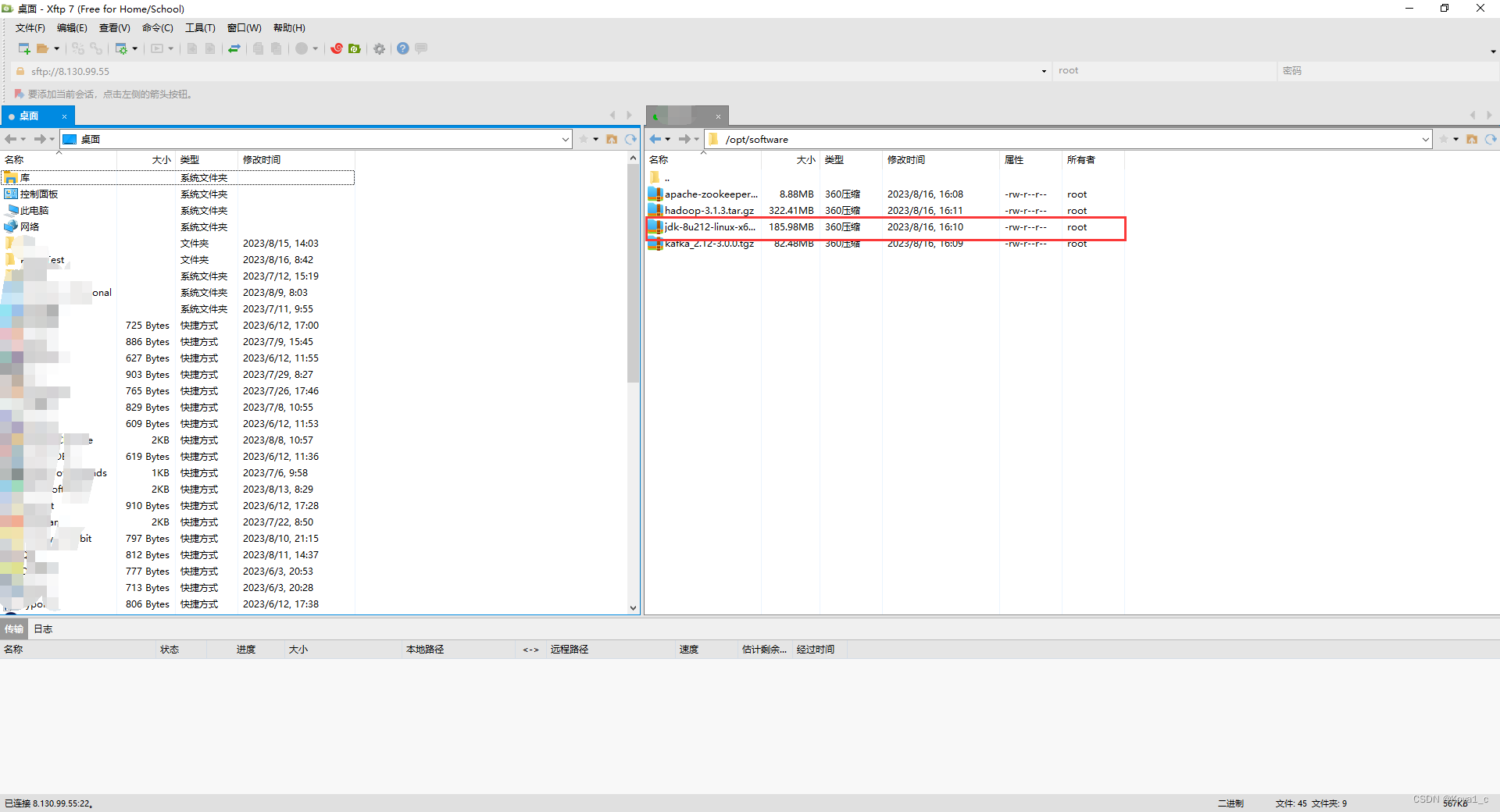
Kafka 集群搭建过程
前言 跟着尚硅谷海哥文档搭建的Kafka集群环境,在此记录一下,侵删 注意:博主在服务器上搭建环境的时候使用的是一个服务器,所以这篇博客可能会出现一些xsync分发到其他服务器时候的错误,如果你在搭建的过程中出现了错…...

【算法随记】在计算过程中模的情况
https://leetcode.cn/problems/power-of-heroes/ 计算过程中,可以放心模的情况: 加减乘 先模再加再模和直接加再模一样 a m o d m b m o d m ≡ a b ( m o d m ) a\mod mb\mod m ≡ ab \ (\mod m) amodmbmodm≡ab (modm) 先模再减再模和直接减再模…...
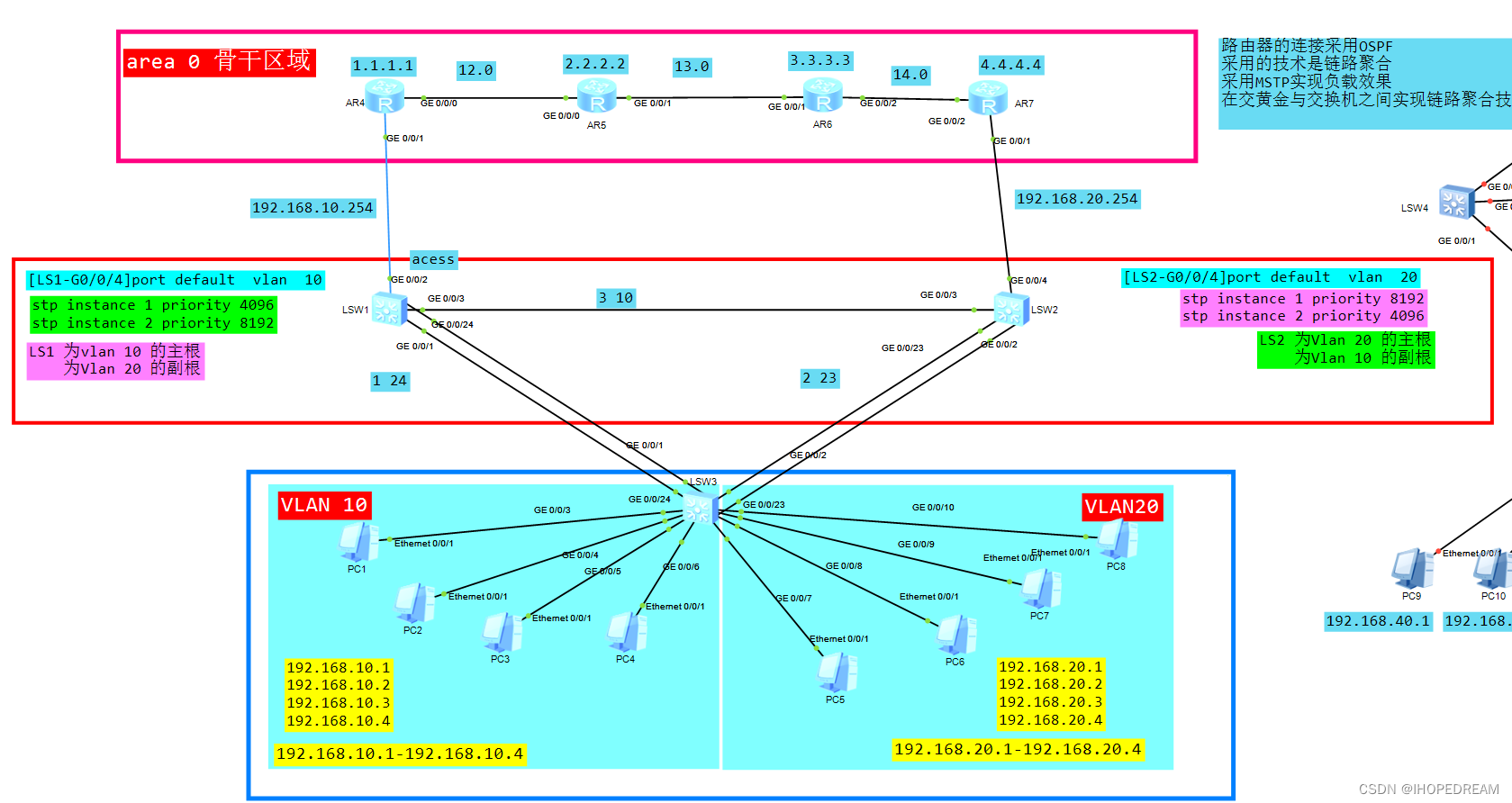
MSTP多生成树协议(第二课)
MSTP负载均衡 实验 需求 1)PC1属于 vlan 10 ,IP地址为 192.168.10.1/24, 网关为 192.168.10.2542)PC2属于 vlan 20 ,IP地址为 192.168.20.1/24, 网关为 192.168.20.254**3)确保PC1与PC2互通4…...

数组指针、函数指针、指针数组、函数 指针数组、指针函数详细总结
1.数组指针概念和应用 首先数组指针应该是一个数组,它的定义如下: 数组指针,指的是数组名的指针,即数组首元素地址的指针。即是指向数组的指针。例:int (*p)[10]; p即为指向数组的指针,又称数组指针。 数…...
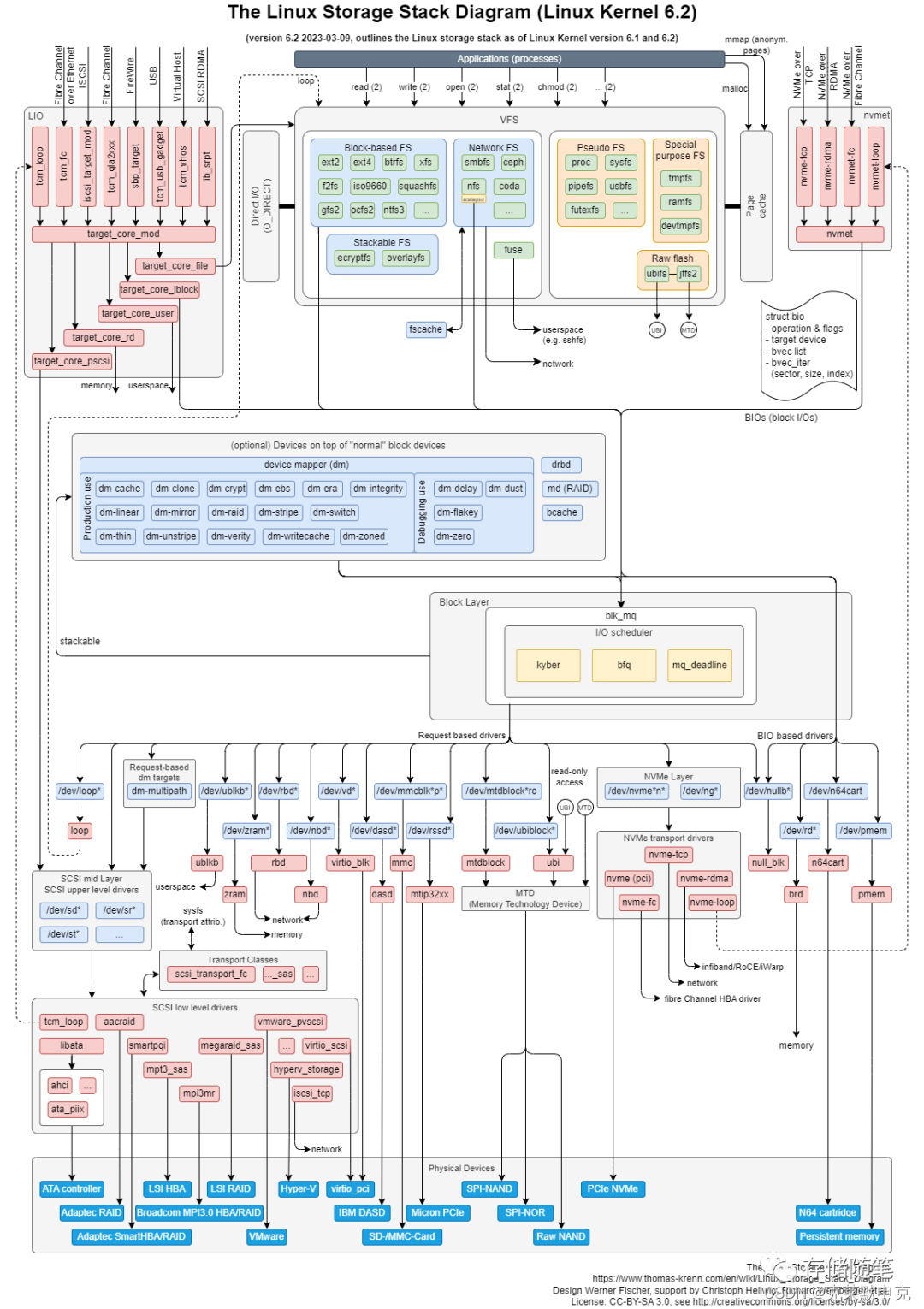
Linux存储学习笔记
相关文章 Linux 存储系列|请描述一下文件的 io 栈? - tcpisopen的文章 - 知乎 https://zhuanlan.zhihu.com/p/478443978 深入学习 Linux 操作系统的存储 IO 堆栈 - KaiwuDB的文章 - 知乎 https://zhuanlan.zhihu.com/p/636720297 linux存储栈概览 - st…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

【AI学习】三、AI算法中的向量
在人工智能(AI)算法中,向量(Vector)是一种将现实世界中的数据(如图像、文本、音频等)转化为计算机可处理的数值型特征表示的工具。它是连接人类认知(如语义、视觉特征)与…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...
)
【RockeMQ】第2节|RocketMQ快速实战以及核⼼概念详解(二)
升级Dledger高可用集群 一、主从架构的不足与Dledger的定位 主从架构缺陷 数据备份依赖Slave节点,但无自动故障转移能力,Master宕机后需人工切换,期间消息可能无法读取。Slave仅存储数据,无法主动升级为Master响应请求ÿ…...

汇编常见指令
汇编常见指令 一、数据传送指令 指令功能示例说明MOV数据传送MOV EAX, 10将立即数 10 送入 EAXMOV [EBX], EAX将 EAX 值存入 EBX 指向的内存LEA加载有效地址LEA EAX, [EBX4]将 EBX4 的地址存入 EAX(不访问内存)XCHG交换数据XCHG EAX, EBX交换 EAX 和 EB…...

3-11单元格区域边界定位(End属性)学习笔记
返回一个Range 对象,只读。该对象代表包含源区域的区域上端下端左端右端的最后一个单元格。等同于按键 End 向上键(End(xlUp))、End向下键(End(xlDown))、End向左键(End(xlToLeft)End向右键(End(xlToRight)) 注意:它移动的位置必须是相连的有内容的单元格…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

PostgreSQL——环境搭建
一、Linux # 安装 PostgreSQL 15 仓库 sudo dnf install -y https://download.postgresql.org/pub/repos/yum/reporpms/EL-$(rpm -E %{rhel})-x86_64/pgdg-redhat-repo-latest.noarch.rpm# 安装之前先确认是否已经存在PostgreSQL rpm -qa | grep postgres# 如果存在࿰…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...
的打车小程序)
基于鸿蒙(HarmonyOS5)的打车小程序
1. 开发环境准备 安装DevEco Studio (鸿蒙官方IDE)配置HarmonyOS SDK申请开发者账号和必要的API密钥 2. 项目结构设计 ├── entry │ ├── src │ │ ├── main │ │ │ ├── ets │ │ │ │ ├── pages │ │ │ │ │ ├── H…...
