E - Excellent Views
Problem - E - Codeforces
问题描述:数组H大小都不相同。从i到j是可行的,当且仅当
不存在 k ,使 ∣ i − k ∣ ≤ ∣ i − j ∣ , H k > H j 不存在k,使 \\ |i - k| \leq |i - j|, \quad H_k > H_j 不存在k,使∣i−k∣≤∣i−j∣,Hk>Hj
暴力 O(n * n),从当前点向两边进行扩散。
void solve() {int n;cin>>n;for(int i = 1; i <= n; ++i) cin>>a[i];for(int i = 1; i <= n; ++i) {int ma = -INF;int cnt = 0;int len = max(i - 1, n - i);for(int j = 0; j <= len; ++j) {int lvidx = i - j, rvidx = i + j;if(lvidx < 1) {ma = max({ma, a[rvidx]});if(a[rvidx] >= ma) cnt++;} else {ma = max({ma, a[lvidx], a[rvidx]});if(a[lvidx] >= ma) cnt++;if(a[rvidx] >= ma) cnt++;}}cout<<cnt - 2<<" ";}
}
优化:单调栈,对于i算出到左边和到右边第一个大于下标为i的元素值得长度或下标,用差分对半记录即可。
代码:
#include <iostream>
#include <vector>
#include <string>
#include <cstring>
#include <set>
#include <map>
#include <queue>
#include <ctime>
#include <random>
#include <sstream>
#include <stack>
#include <numeric>
#include <stdio.h>
#include <functional>
#include <bitset>
#include <algorithm>
using namespace std;// #define Multiple_groups_of_examples
#define IOS std::cout.tie(0);std::cin.tie(0)->sync_with_stdio(false);
#define dbgnb(a) std::cout << #a << " = " << a << '\n';
#define dbgtt cout<<" !!!test!!! "<<endl;
#define rep(i,x,n) for(int i = x; i <= n; i++)#define all(x) (x).begin(),(x).end()
#define pb push_back
#define vf first
#define vs secondtypedef long long LL;
typedef pair<int,int> PII;
/*** https://codeforces.com/gym/103185/problem/E* 题意:对每一个i找到满足条件的j, 其中条件为:不存在k, 使 abs(i - k) <= abs(i - j) && Hj < Hk 成立* 解法:std:https://github.com/Diego1149/ICPC-Latam-2020 (好像是用线段树写的* other:https://blog.csdn.net/m0_53807008/article/details/119065842* * 思路:单调栈* 两次单调栈。这里为了简单,假设 1 <= i < j <= n* 第一次找 对于j来说,从i到j中满足条件的元素(这里j是题意中的i。* 第二次找,对于i来说,从i到j中满足条件的元素(这里i就是题意中的i。* e.g. 下标: ... 符合条件的 i 符合条件的 ...* 对于第一次来说:* 比a[i]小的最大元素(记为A)下标找到,将比a[i]小的最大元素下标对应得pre数组赋值 i - 1,表示,最后一个小于A的下标位置。* 对于那个最大元素下标(记为idx),使 idx 对应的元素可以worth的长度为 [idx, i - 1]的一半。* 记录用差分记录即可。* 第二次,倒着来一边,同第一次。
*/
const int INF = 0x3f3f3f3f;
const int N = 2e5 + 21;
int a[N];
int pre[N], suf[N];
int lef[N], rig[N];
void inpfile();
void solve() {int n; cin>>n;for(int i = 1; i <= n; ++i) cin>>a[i];a[n+1] = INF; // 让 n + 1 等于inf, 0 等于inf,因为要让所以的都出栈stack<int> sk;// 考虑a[i]对左边的贡献sk.push(1);for(int i = 2; i <= n+1; ++i) {// 如果当前 H 大于 上一个H,将上一个H对应的下标进行记录while(sk.size() && a[i] > a[ sk.top()]) {pre[ sk.top()] = i - 1; // 将i - 1进行赋值,表示到i - 1 ,大于的条件一直是成立的sk.pop();}sk.push(i);}for(int i = 1; i <= n; ++i) {lef[i+1]++; // 将i + 1 先进行++,表示有一个贡献if(pre[i] != n) // 如果等于n,表示,恒成立,不用--,// 否则,只能到达 (i + pre[i]) / 2 的下标,利用差分 就是 [ r + 1]--lef[ (i + pre[i]) / 2 + 1]--;}// 考虑a[i]对右边的贡献// 思路及代码同上sk.push(n);a[0] = INF;for(int i = n - 1; i >= 0; --i) {while(sk.size() && a[i] > a[ sk.top()]) {suf[ sk.top()] = i + 1;sk.pop();}sk.push(i);}for(int i = 1; i <= n; ++i) {rig[i-1]++;if(suf[i] != 1)rig[ (i + suf[i] + 1) / 2 - 1]--;}// 差分前缀和for(int i = 1; i <= n; ++i) lef[i] += lef[i-1];for(int i = n; i >= 1; --i) rig[i] += rig[i+1];for(int i = 1; i <= n; ++i) cout<<lef[i] + rig[i]<<" ";
}
int main()
{#ifdef Multiple_groups_of_examplesint T; cin>>T;while(T--)#endifsolve();return 0;
}
void inpfile() {#define mytest#ifdef mytestfreopen("ANSWER.txt", "w",stdout);#endif
}
Gym - 103185E E - Excellent Views_流锡的博客-CSDN博客
相关文章:

E - Excellent Views
Problem - E - Codeforces 问题描述:数组H大小都不相同。从i到j是可行的,当且仅当 不存在 k ,使 ∣ i − k ∣ ≤ ∣ i − j ∣ , H k > H j 不存在k,使 \\ |i - k| \leq |i - j|, \quad H_k > H_j 不存在k,使…...

WiFi天线和NB-IoT天线不通用
表面看起来完全一样。但是把WiFi天线插到NB-IoT设备后,信号弱了很多。还导致设备反复重启...
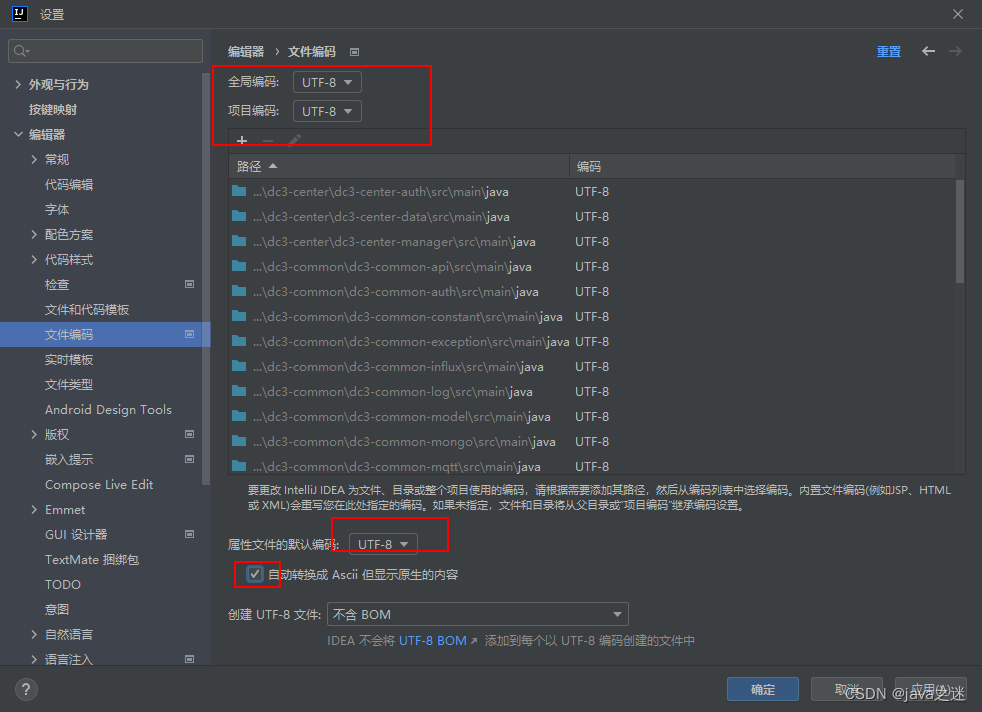
IoT DC3 是一个基于 Spring Cloud 的开源的、分布式的物联网(IoT)平台本地部署步骤
dc3 windows 本地搭建步骤: 必要软件环境 进入原网页# 务必保证至少需要给 docker 分配:1 核 CPU 以及 4G 以上的运行内存! JDK : 推荐使用 Oracle JDK 1.8 或者 OpenJDK8,理论来说其他版本也行; Maven : 推荐…...
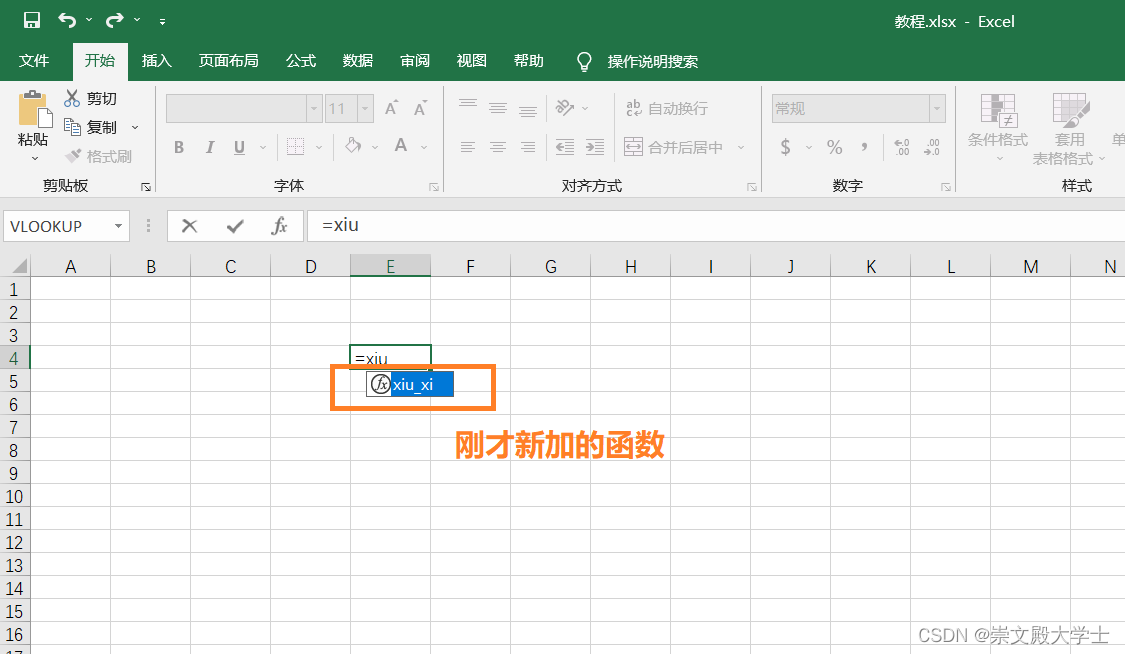
VBA Excel自定义函数的使用 简单的语法
一个简单的教程,实现VBA自定义函数。 新建模块 复制后面的代码放进来 函数的入口参数不定义,则认为是一块区域; 反之,如FindChar1 As String,则认为是输入的单值。 循环和分支如下例子,VB比较接近自然语…...

字节跳动 从需求到上线全流程 软件工程流程 需求评估 MVP
走进后端开发流程 整个课程会带大家先从理论出发,思考为什么有流程 大家以后工作的团队可能不一样,那么不同的团队也会有不同的流程,这背后的逻辑是什么 然后会带大家按照走一遍从需求到上线的全流程,告诉大家在流程的每个阶段&am…...

线性代数-矩阵的本质
线性代数-矩阵的本质 线性代数-矩阵的本质...
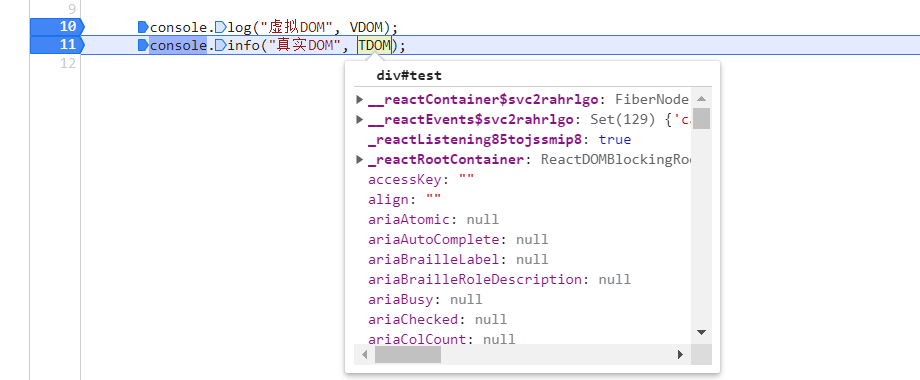
React基础入门之虚拟Dom
React官方文档:https://react.docschina.org/ 说明 重要提示:本系列文章基础篇总结自尚硅谷课程,且采用类式写法!!最新的函数式组件写法见高级篇。 本系列文档旨在帮助vue同学更快速的学习react,如果你很…...
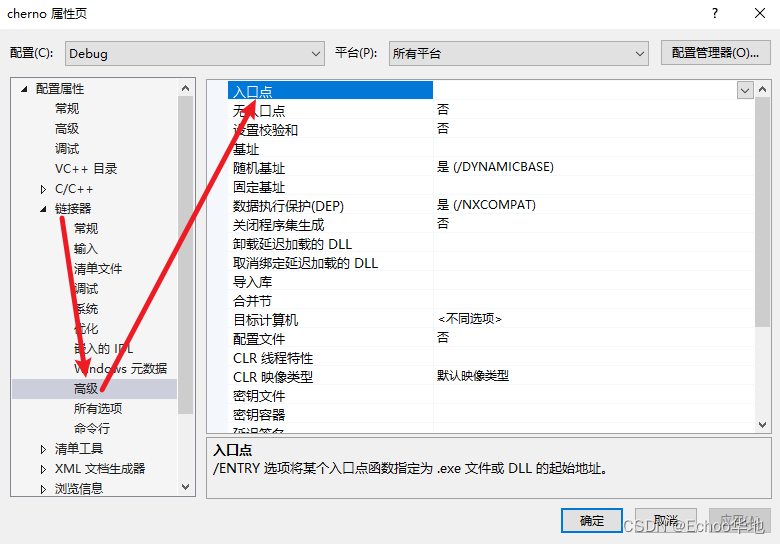
C++基础Ⅰ编译、链接
目录儿 1 C是如何工作的1.1 预处理语句1.2 include1.3 main()1.4 编译单独编译项目编译 1.5 链接 2 定义和调用函数3 编译器如何工作3.1 编译3.1.1 引入头文件系统头文件自定义头文件 3.1.2 自定义类型3.1.3 条件判断拓展: 汇编 3.2 链接3.2.1 起始函数3.2.2 被调用的函数 3.3 …...

VMware和ubuntu配置Hadoop环境
目录 一、获取VMware安装包 1、官网获取 1)首先先进入官网,官网首页是下面这样: 2)接着点击产品选项 3)进入后点击查看所有产品,然后在右上角选择排序方式为Z到A,然后向下滑动找到Workstation…...
uview2.0自定义tabbar
tabbar组件 <template><u-tabbar :value"tab" change"changeTab" :fixed"true" :border"true" :placeholder"true":safeAreaInsetBottom"true"><u-tabbar-item text"消息" icon"c…...
Star History 月度开源精选|Llama 2 及周边生态特辑
7 月 18 日,Meta 发布了 Llama,大语言模型 Llama 1 的进阶版,可以自由免费用于研究和商业,支持私有化部署。 所以本期 Star History 的主题是:帮助你快速把 Llama 2 在自己机器上跑起来的开源工具,无论你的…...

修改电脑上路由表使笔记本默认走无线
如果笔记本上即连接了有线,也连接了无线,默认电脑会走有线的,通过route print命令查看路由表就可以看出来,因为无线的“metric”跳数要比有线的高 解决方法: 如果想实现让默认走无线,就需要修改自己电脑的…...

Spring Cache的介绍以及怎么使用(redis)
Spring Cache 文章目录 Spring Cache1、Spring Cache介绍2、Spring Cache常用注解2.1、EnableCaching注解2.2、CachePut注解2.3、CacheEvict注解2.4、Cacheable注解 3、Spring Cache使用方式--redis 1、Spring Cache介绍 Spring Cache是一个框架,实现了基于注解的缓…...

软考高级系统架构设计师系列论文六十九:论信息系统的安全风险评估
一、信息系统相关知识点 软考高级信息系统项目管理师系列之四十三:信息系统安全管理软考高级系统架构设计师:系统安全分析与设计...
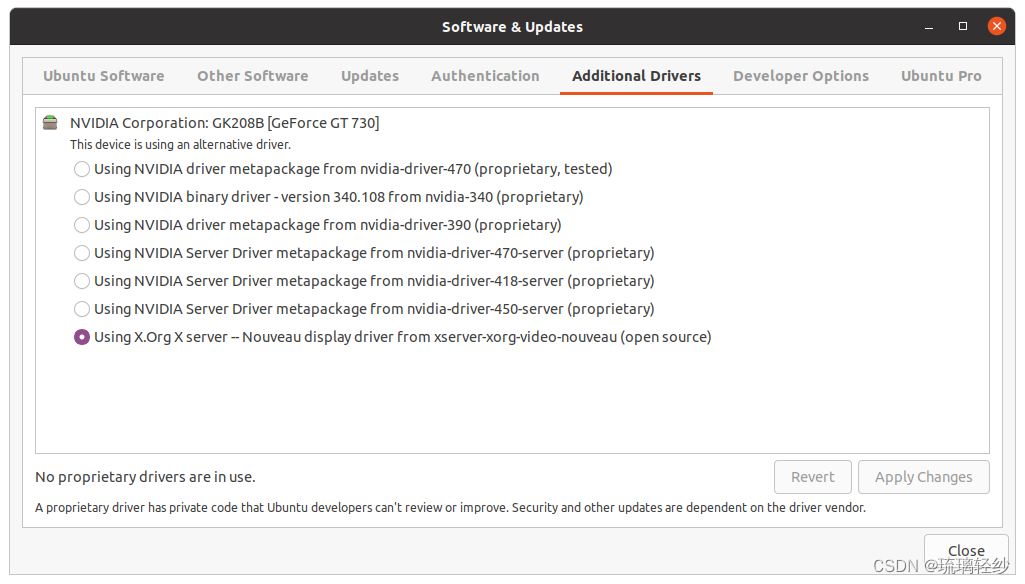
Ubuntu系统安装之后首需要做的事情
Ubuntu系统的初步环境搭建 1、换源2、显卡3、浏览器4、输入法5、终端6、ROS7、VSCode8、设置时间与win一致9、 TimeShift10、 Anaconda(考虑装不装) 1、换源 点开Software&&Update,找到Ubuntu Software中的Download from,…...

Qt——QPushButton控件的常见属性、方法和信号
Qt中QPushButton控件的常见属性、方法和信号 一、QPushButton控件常见属性 一、QPushButton控件常见方法 一、QPushButton控件常见信号 一、QPushButton控件常见属性(Properties) 1. text: 描述:按钮上显示的文本。 用法: butto…...
5.5 基于ISOLAR-A的系统级设计与配置方法(上))
AUTOSAR规范与ECU软件开发(实践篇)5.5 基于ISOLAR-A的系统级设计与配置方法(上)
目录 前言 1 系统配置输入文件创建与导入 2、 Composition SWC建立 前言 如前所述, AUTOSAR支持整车级别的软件架构设计, 开发人员可以进行整车级别的软件组件定义, 再将这些软件组件分配到各个ECU中, 这就是AUTOSAR系统级设计需要完成的主要任务。 下面结合AUTOSAR方法论…...
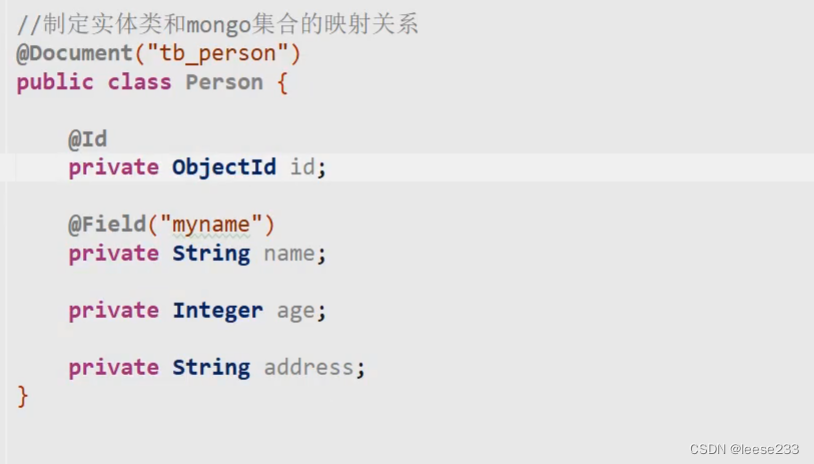
mongoDB的CRUD
...
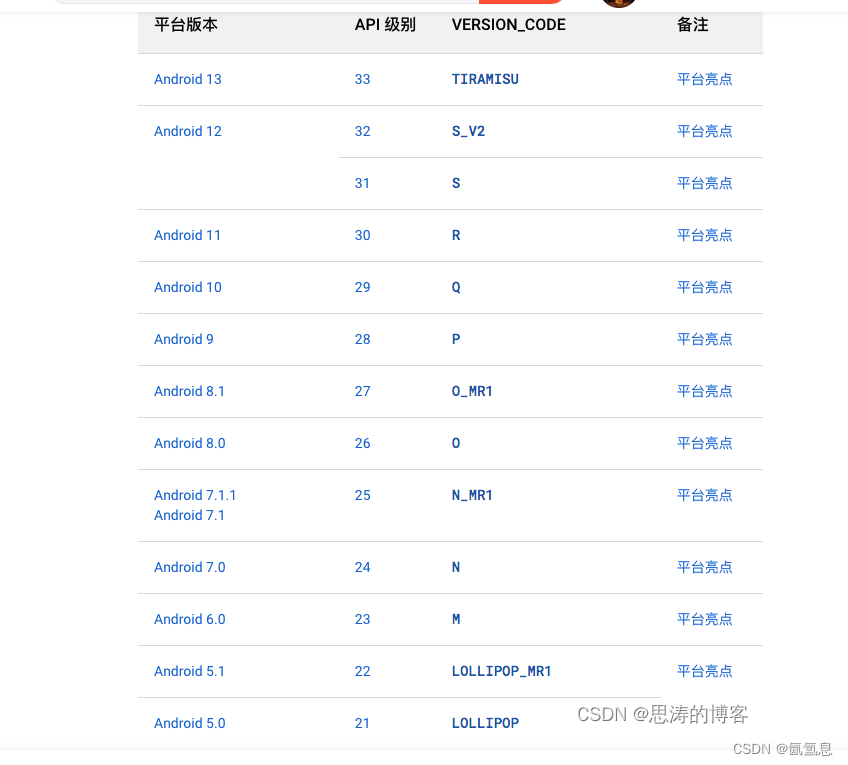
flutter TARGET_SDK_VERSION和android 13
config.gradle ext{SDK_VERSION 33MIN_SDK_VERSION 23TARGET_SDK_VERSION 33COMPILE_SDK_VERSION SDK_VERSIONBUILD_TOOL_VERSION "33.0.0"//兼容库版本SUPPORT_LIB_VERSION "33.0.0"}app/build.gradle里面的 defaultConfig {// TODO: Specify your…...

大数据Flink(六十六):Flink的重要概念和小结
文章目录 Flink的重要概念和小结 一、数据流图(Dataflow Graph)...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

基于ASP.NET+ SQL Server实现(Web)医院信息管理系统
医院信息管理系统 1. 课程设计内容 在 visual studio 2017 平台上,开发一个“医院信息管理系统”Web 程序。 2. 课程设计目的 综合运用 c#.net 知识,在 vs 2017 平台上,进行 ASP.NET 应用程序和简易网站的开发;初步熟悉开发一…...

Objective-C常用命名规范总结
【OC】常用命名规范总结 文章目录 【OC】常用命名规范总结1.类名(Class Name)2.协议名(Protocol Name)3.方法名(Method Name)4.属性名(Property Name)5.局部变量/实例变量(Local / Instance Variables&…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

A2A JS SDK 完整教程:快速入门指南
目录 什么是 A2A JS SDK?A2A JS 安装与设置A2A JS 核心概念创建你的第一个 A2A JS 代理A2A JS 服务端开发A2A JS 客户端使用A2A JS 高级特性A2A JS 最佳实践A2A JS 故障排除 什么是 A2A JS SDK? A2A JS SDK 是一个专为 JavaScript/TypeScript 开发者设计的强大库ÿ…...

招商蛇口 | 执笔CID,启幕低密生活新境
作为中国城市生长的力量,招商蛇口以“美好生活承载者”为使命,深耕全球111座城市,以央企担当匠造时代理想人居。从深圳湾的开拓基因到西安高新CID的战略落子,招商蛇口始终与城市发展同频共振,以建筑诠释对土地与生活的…...

【从零学习JVM|第三篇】类的生命周期(高频面试题)
前言: 在Java编程中,类的生命周期是指类从被加载到内存中开始,到被卸载出内存为止的整个过程。了解类的生命周期对于理解Java程序的运行机制以及性能优化非常重要。本文会深入探寻类的生命周期,让读者对此有深刻印象。 目录 …...

代码规范和架构【立芯理论一】(2025.06.08)
1、代码规范的目标 代码简洁精炼、美观,可持续性好高效率高复用,可移植性好高内聚,低耦合没有冗余规范性,代码有规可循,可以看出自己当时的思考过程特殊排版,特殊语法,特殊指令,必须…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...
