DAY24
题目一

啊 看着挺复杂 其实很简单
第一种方法
就是纵轴是怪兽编号 横轴是能力值
看看能不能打过
逻辑很简单 看看能不能打得过 打过的就在花钱和直接打里面取小的 打不过就只能花钱
这种方法就导致 如果怪兽的能力值很大 那么我们就需要很大的空间
所以引出下一种做法
纵轴是怪兽编号 横轴是钱数
我们对比一下这两种方法
1.当能力值大 钱小的情况 第一种方法浪费空间 第二种不浪费
2.当能力值小 钱多的情况 第二种浪费 第一种不浪费
所以 根据数况来取
dp[i][j] 表示正好花j元能不能打过怪兽 打不过-1 打得过就是你目前的能力值
状态转移
如果 dp[i-1][j]位置的值 大于等于当前怪兽的 能力值 那么dp[i][j]==dp[i-1][j]
如果 不大于等于 那看这个怪兽 假如说能力值是x 那就得找dp[i-1][j-x]的值 然后加上怪兽的能力
就是说 我看看打到上一个怪兽 最少需要多少钱 那么我再加上多少钱就是打败这个怪兽的值
方法一
public static long process(int[] d, int[] p, int ability, int index) {if (index == d.length) {return 0;}if (ability < d[index]) {return p[index] + process(d, p, ability + d[index], index + 1);} else { // 可以贿赂,也可以不贿赂return Math.min(p[index] + process(d, p, ability + d[index], index + 1),process(d, p, ability, index + 1));}}public static long func1(int[] d, int[] p) {return process(d, p, 0, 0);}这局部最优整体也最优吗 我想想 如果当前选择了直接打这个怪兽而获得它的能力 正好导致下一个很贵的怪兽必须花钱买怎么办
2 2 1 5
2 花钱 2直接打 1直接打 5花钱 7块
2买 2买 1买 5打 花五块
我开始以为的递归是 每一步局部最优2 花钱 2直接打 1直接打 5花钱 7块 就像这种
但实际的流程是 用动态规划来看 我这个点的钱数 是依赖于前面的最少花的钱数再加上此点最少花的钱数
动态规划
public static long func2(int[] d, int[] p) {int sum = 0;for (int num : d) {sum += num;}long[][] dp = new long[d.length + 1][sum + 1];for (int i = 0; i <= sum; i++) {dp[0][i] = 0;}for (int cur = d.length - 1; cur >= 0; cur--) {for (int hp = 0; hp <= sum; hp++) {// 如果这种情况发生,那么这个hp必然是递归过程中不会出现的状态// 既然动态规划是尝试过程的优化,尝试过程碰不到的状态,不必计算if (hp + d[cur] > sum) {continue;}if (hp < d[cur]) {dp[cur][hp] = p[cur] + dp[cur + 1][hp + d[cur]];} else {dp[cur][hp] = Math.min(p[cur] + dp[cur + 1][hp + d[cur]], dp[cur + 1][hp]);}}}return dp[0][0];}这个动态规划怎么考虑 感觉从原来的 递归考虑好一点 直接改就可以了 也就是第一层递归出结果 dp[0][0] 我把这个任务交给你..... 这压根就是递归硬改的动态规划(精细化搜索)
和正常的从左往右尝试模型有什么不同呢?之前是一个数(钱 或者 容量)越来越少 现在是从零开始越来越多
也为我提供了个思路 不行直接写递归 再改动态规划 复习一下 本质上动态规划使用数组保存结果 减少计算次数
方法二
这次横轴是钱 dp[i][j]的位置表示严格花j块钱 通过了0....i的怪物获得的最大能力值
严格花j元 那就是说多了也不行 8块钱能通过j==9都不行
然后推到最后一行 从左后一行里面找最左面不为-1的值
最后一行的意义是 解决掉所有怪物花的钱数 我们实际上遍历了所有可以解决掉所有怪物的方法
为什么是严格花多少钱也就出在这里
如果不是严格花多少多少钱 我们最后得出来的结果就不是 解决掉怪物的所有可能了 每一步递推过来就是错的
如果不是严格的 就说明这种组合是无效的 大于也不行 大于抓过的结果 我们之前肯定花很少的钱抓过了 而且我们最后需要的答案是每一种组合 花钱最少的 不严格算是什么样子 在某些情况下不严格不一定是错的 但是严格一定是对的
不可置否的乱写
假如说我dp[i][j] 位置往前找dp[i - 1][j - p[i]] 它是说打上一个怪物花了这么些钱能打过 它不为-1我们就加上了 i-1怪兽要10块钱 然后我们是不严格的 dp[j-p[i]]打到+11的位置上面了 本来应该是-1 现在不为-1 那我们这个位置就变成了直接花钱买 因为是取武力值大的 所以直接当前武力值加上 作为结果
但实际上 这个位置的结果是不可以加上武力值的 就是说 我们不能严格花这个钱解决这个怪兽
如果这个位置是底层的第一个不为-1 那么寄
public static int func(int [] d,int [] p) {int sum = 0;for (int i : p) {sum += i;}int [][] dp = new int [d.length+1][sum+1];for(int i = 0;i<d.length;i++) {for(int j = 0;j<sum+1;j++) {dp[i][j] = -1;}}dp[0][p[0]] = d[0];//第一行只有这个位置有值for(int i = 1;i<d.length;i++) {for(int j = 0;j<sum+1;j++) {if(j>=p[i]&&dp[i - 1][j - p[i]] != -1){//j-p[i]不越界dp[i][j] = dp[i - 1][j - p[i]] + d[i];}if(dp[i-1][j]>=d[i]) {dp[i][j] = Math.max(dp[i][j], dp[i - 1][j]);}//为什么要取一个能力最大的呢 这个位置的钱已经定好了 我就一定花这么多钱 为啥不取个能力大的//这里不用担心 哎呀 我直接买 那岂不是肯定比不买的能力值大吗 注意 这里的钱是一定的 如果这个没买 那么就有其他的钱花在别处}}int ans = 0;for (int j = 0; j <= sum; j++) {if (dp[d.length - 1][j] != -1) {ans = j;break;}}return ans;}题目二
给你一个字符串 s ,每一次操作你都可以在字符串的任意位置插入任意字符。
请你返回让 s 成为回文串的 最少操作次数 。
来一个dp数组 纵轴是L 横轴是R dp[i][j]表示i...j上需要添加多少字符
每个依赖为: 如果i位置字符等于j位置字符 那么不需要添加 =
如果不等于 那就要看看是在末尾补还是在头部补的操作次数少了
我自己用acbca推了一遍 就是说 当L=0 R=4 的时候怎么求 如果我a==a那就看cbc是怎么变回文的
acb怎么变回文 那就要看ac是怎么变的 cb是怎么变的 在除去开头/结尾的情况下先把它变成回文 然后我们只需要考虑这不是回文的一个字符(就是加上)就可以了
我之前比较困惑的是bab 如果 我在做ba的时候 我直接在后面加了一个b 那我还要也就是变成了bab 已经是回文了 那我这个原本的b怎么处理呢?
如果是bab 在推ba的时候 我们或许会在前面加a 或许会在后面补b 但是如果b==a了 那我们就要看a是怎么变回文串的 而不是ba怎么变的
第三题
一种消息接收并打印的结构设计已知一个消息流会不断地吐出整数1~N,但不一定按照顺序吐出。如果上次打印的数为i,那么当i+1出现时,请打印i+1及其之后接收过的并且连续的所有数,直到1~N全部接收并打印完,请设计这种接收并打印的结构。初始时默认i==0
多个空间
比如最开始我们加入 1 3 5 7四个点
那就模拟四个空间
1开头1结尾的
3开头3结尾的
5开头5结尾的
7开头7结尾的
假如说我们来了一个6 它的开头就是6 那我们就去找结尾为5的区间 把他们连在一起
同时维护一个指针 这个指针是指播放到哪个位置了 在哪里卡住了
class Node {public String info;public Node next;public Node(String str) {info = str;}
}class Messagebox {private HashMap<Integer, Node> headMap;private HashMap<Integer, Node> tailMap;private int waitPoint;public Messagebox() {headMap = new HashMap<Integer, Node>();tailMap = new HashMap<Integer, Node>();waitPoint = 1;}public void receive(int num, String info) {if (num < 1) {return;}Node cur = new Node(info);headMap.put(num, cur);tailMap.put(num, cur);// 建立了num~num这个连续区间的头和尾// 查询有没有某个连续区间以num-1结尾if (tailMap.containsKey(num - 1)) {tailMap.get(num - 1).next = cur;tailMap.remove(num - 1);//如果它能接在某个区间的尾部headMap.remove(num);}// 查询有没有某个连续区间以num+1开头的if (headMap.containsKey(num + 1)) {cur.next = headMap.get(num + 1);tailMap.remove(num);//如果它能接在某个区间的头部headMap.remove(num + 1);}if (num == waitPoint) {print();}}private void print() {Node node = headMap.get(waitPoint);headMap.remove(waitPoint);while (node != null) {System.out.print(node.info + " ");node = node.next;waitPoint++;}tailMap.remove(waitPoint-1);System.out.println();}
}相关文章:

DAY24
题目一 啊 看着挺复杂 其实很简单 第一种方法 就是纵轴是怪兽编号 横轴是能力值 看看能不能打过 逻辑很简单 看看能不能打得过 打过的就在花钱和直接打里面取小的 打不过就只能花钱 这种方法就导致 如果怪兽的能力值很大 那么我们就需要很大的空间 所以引出下一种做法 纵…...
Redis过期数据的删除策略
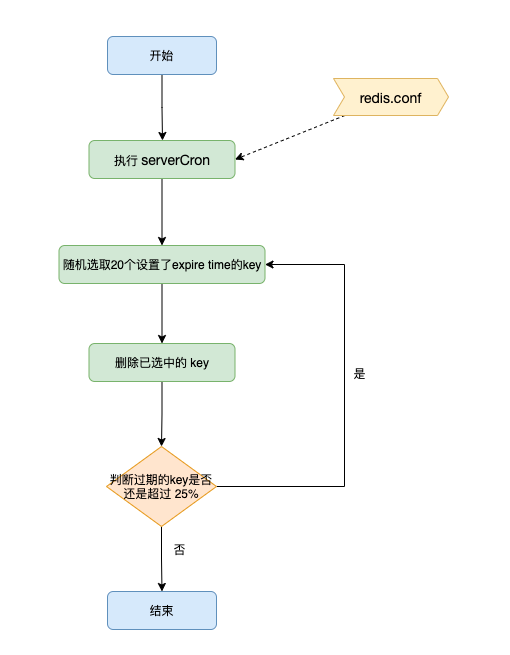
1 介绍 Redis 是一个kv型数据库,我们所有的数据都是存放在内存中的,但是内存是有大小限制的,不可能无限制的增量。 想要把不需要的数据清理掉,一种办法是直接删除,这个咱们前面章节有详细说过;另外一种就是…...

如何使用CSS实现一个拖拽排序效果?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 实现拖拽排序效果的CSS和JavaScript示例⭐ HTML 结构⭐ CSS 样式 (styles.css)⭐ JavaScript 代码 (script.js)⭐ 实现说明⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦…...

leetcode 118.杨辉三角
⭐️ 题目描述 🌟 leetcode链接:https://leetcode.cn/problems/pascals-triangle/description/ 代码: class Solution { public:vector<vector<int>> generate(int numRows) {// 先开空间vector<vector<int>> v;v.…...

微服务框架之SpringBoot面试题汇总
微服务框架之SpringBoot面试题汇总 什么是Spring Boot? 多年来,随着新功能的增加,spring变得越来越复杂。Spring项目,我们必须添加构建路径或添加Maven依赖关系,配置应用程序服务器,添加spring配置。因此&…...

Promise详解
目录 一、前言:为什么会出现Promise?二、Promise是什么?2.1 Promise的初体验 三、使用Promise的好处?3.1 指定回调函数的方式更加灵活3.2 可以解决回调地狱问题,支持链式调用 四、Promise实例对象的两个属性五、resolve函数以及reject函数六、Promise…...

Oracle 查询(当天,月,年)的数据
Trunc 在oracle中,可利用 trunc函数 查询当天数据,该函数可用于截取时间或者数值,将该函数与 select 语句配合使用可查询时间段数据 查询当天数据 --sysdate是获取系统当前时间函数 --TRUNC函数用于截取时间或者数值,返回指定的…...
什么是梯度下降
什么是梯度下降 根据已有数据的分布来预测可能的新数据,这是回归 希望有一条线将数据分割成不同类别,这是分类 无论回归还是分类,我们的目的都是让搭建好的模型尽可能的模拟已有的数据 除了模型的结构,决定模型能否模拟成功的关键…...
开黑啦kook 机器人开发 PHP swoole Liunx 服务器(宝塔)
安装环境 PHP 拓展 直接使用 宝塔一键安装 (Windows系统不支持) 设置命令行的PHP版本避免执行脚本时 获取不到 swoole 检查swoole是否安装成功 获取官方SDK GitHub - kaiheila/php-bot: 开黑啦机器人的php版本https://github.com/kaiheila/php-bot 配…...
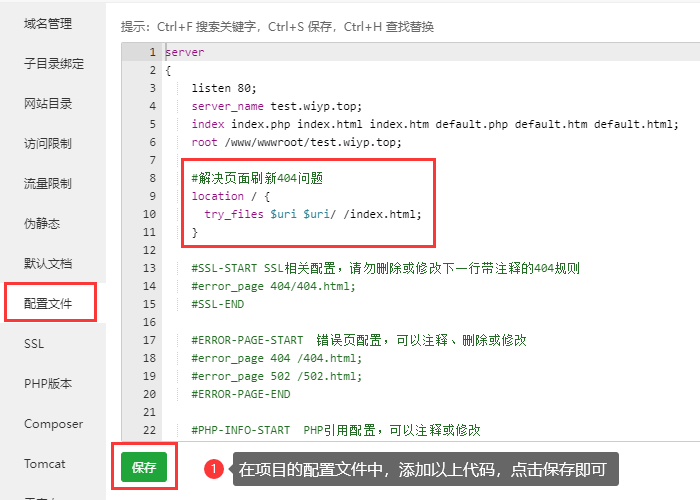
Vue 中hash 模式与 history 模式的区别
hash 模式: - 地址中永远带着 # 号,不美观。 - 兼容性比较好。 - 通过手机 app 分享地址时,如果 app 效验严格,该地址会被标记为不合法。 history 模式: - 地址干净,美观。 - 兼容性和 hash 模式相比…...
Dockerfile推送私有仓库的两个案例
一,编写Dockerfile制作Web应用系统nginx镜像,生成镜像nginx:v1.1,并推送其到私有仓库。 具体要求如下: (1)基于centos基础镜像; (2)指定作者信息; ÿ…...

【指标】指标公式大全,款款经典(建议珍藏)!-神奇指标网
三、指标源码: 1、连续三天高开高走的选股公式 count(o〉ref(c,1)andc>o,3)3; 2、连续3天每天的最低价都比前一天高 count(l〉ref(c,1),3)3; 3、周量缩小50%或40%或n&#x…...

面试题目收集
Zset排行榜功能如何设计key? key就设计成排行榜的名字,比如下面插入或者更新数据 Long zadd(final String key, final double score, final String member) key : 排行榜的名字 memeber : 用户 score : 用户的分数 项目…...

创建R包-2.1:在RStudio中使用Rcpp制作R-Package(更新于2023.8.23)
目录 0-前言 1-在RStudio中创建R包项目 2-创建R包 2.1通过R函数创建新包 2.2在RStudio通过菜单来创建一个新包 2.3关于R包创建的说明 3-添加R自定义函数 4-添加C函数 0-前言 目标:在RStudio中创建一个R包,这个R包中包含C函数,接口是Rc…...
chatGPT如何解释泽众PerformanceRunner性能测试工具?
PerformanceRunner 是一个性能测试工具,可以帮助测试人员进行性能测试。它的主要功能包括: 1. 脚本录制和回放: PerformanceRunner可以录制 HTTP/HTTPS 通信协议的脚本,并能够回放模拟真实用户的行为。通过录制和回放,…...

LA@向量组线性相关性
文章目录 向量组线性相关性线性相关线性无关多向量向量组线性相关单向量向量组的线性相关性单位向量向量组线性相关性双向量向量组的线性相关性双向量线性相关的几何意义三向量线性相关的几何意义包含零向量的向量组线性相关概念迁移:线性方程组和线性相关齐次线性方程组和向量…...

[k8s] 基于ubuntu22部署k8s1.28记录
k8s1.28部署已经不依赖docker了,所以不需要安装docker。同理:如果想查看镜像和运行容器,也不能用docker命令去查询了:需要使用crictl。不过crictl命令参数兼容docker,所以使用上手没有啥难度。 1. 配置安装源 根据k8…...

React 事件代理 和原生事件绑定混用:你的选择会导致什么问题?
在React开发中,事件处理是一个常见的任务。React提供了一个方便的事件系统,但有时我们可能会在React组件中与原生DOM事件一起使用。本文将讨论React的事件代理机制与原生事件绑定混用可能导致的一些问题。 React的事件代理 React采用了一种称为"事…...

使用阿里云国外和国内云服务器有什么注意事项?
使用阿里云的国外和国内云服务器时,有一些注意事项需要考虑: 地理位置:选择离你的用户或数据中心最近的地理位置,可以减少延迟和提高访问速度。对于国内用户,使用国内云服务器可能更好;对于国外用户&#…...
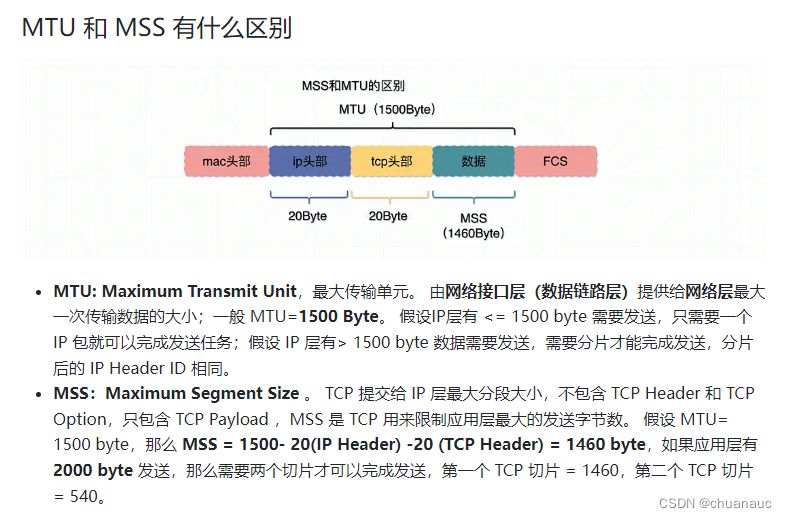
【计算机网络】【常考问题总结】
1. ping 127.0.0.1 后会发生什么? ping 127.0.0.1 ;ping 0.0.0.0 ; ping localhost 面试官问:断网了,还能ping通 127.0.0.1 吗?为什么?_kevin_tech的博客-CSDN博客 2. MTU,MMU是…...

[2025CVPR]DeepVideo-R1:基于难度感知回归GRPO的视频强化微调框架详解
突破视频大语言模型推理瓶颈,在多个视频基准上实现SOTA性能 一、核心问题与创新亮点 1.1 GRPO在视频任务中的两大挑战 安全措施依赖问题 GRPO使用min和clip函数限制策略更新幅度,导致: 梯度抑制:当新旧策略差异过大时梯度消失收敛困难:策略无法充分优化# 传统GRPO的梯…...

【Python】 -- 趣味代码 - 小恐龙游戏
文章目录 文章目录 00 小恐龙游戏程序设计框架代码结构和功能游戏流程总结01 小恐龙游戏程序设计02 百度网盘地址00 小恐龙游戏程序设计框架 这段代码是一个基于 Pygame 的简易跑酷游戏的完整实现,玩家控制一个角色(龙)躲避障碍物(仙人掌和乌鸦)。以下是代码的详细介绍:…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...
)
React Native 导航系统实战(React Navigation)
导航系统实战(React Navigation) React Navigation 是 React Native 应用中最常用的导航库之一,它提供了多种导航模式,如堆栈导航(Stack Navigator)、标签导航(Tab Navigator)和抽屉…...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...

智能分布式爬虫的数据处理流水线优化:基于深度强化学习的数据质量控制
在数字化浪潮席卷全球的今天,数据已成为企业和研究机构的核心资产。智能分布式爬虫作为高效的数据采集工具,在大规模数据获取中发挥着关键作用。然而,传统的数据处理流水线在面对复杂多变的网络环境和海量异构数据时,常出现数据质…...

Go语言多线程问题
打印零与奇偶数(leetcode 1116) 方法1:使用互斥锁和条件变量 package mainimport ("fmt""sync" )type ZeroEvenOdd struct {n intzeroMutex sync.MutexevenMutex sync.MutexoddMutex sync.Mutexcurrent int…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...
 + 力扣解决)
LRU 缓存机制详解与实现(Java版) + 力扣解决
📌 LRU 缓存机制详解与实现(Java版) 一、📖 问题背景 在日常开发中,我们经常会使用 缓存(Cache) 来提升性能。但由于内存有限,缓存不可能无限增长,于是需要策略决定&am…...

基于Java+VUE+MariaDB实现(Web)仿小米商城
仿小米商城 环境安装 nodejs maven JDK11 运行 mvn clean install -DskipTestscd adminmvn spring-boot:runcd ../webmvn spring-boot:runcd ../xiaomi-store-admin-vuenpm installnpm run servecd ../xiaomi-store-vuenpm installnpm run serve 注意:运行前…...
