回文子串-中心拓展
给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。
回文字符串 是正着读和倒过来读一样的字符串。
子字符串 是字符串中的由连续字符组成的一个序列。
具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不同的子串。
示例 1:
输入:s = “abc”
输出:3
解释:三个回文子串: “a”, “b”, “c”
示例 2:输入:s = “aaa”
输出:6
解释:6个回文子串: “a”, “a”, “a”, “aa”, “aa”, “aaa”提示:
1 <= s.length <= 1000
s 由小写英文字母组成
计算有多少个回文子串的最朴素方法就是枚举出所有的回文子串,而枚举出所有的回文字串又有两种思路,分别是:
-
枚举出所有的子串,然后再判断这些子串是否是回文;
-
枚举每一个可能的回文中心,然后用两个指针分别向左右两边拓展,当两个指针指向的元素相同的时候就拓展,否则停止拓展。
假设字符串的长度为 n。我们可以看出前者会用 O ( n 2 ) O(n^2) O(n2) 的时间枚举出所有的子串 s [ l i . . . r i ] s[l_i...r_i] s[li...ri], 然后再用 O ( r i − l i + 1 ) O(r_i - l_i + 1) O(ri−li+1) 的时间检测当前的子串是否是回文,整个算法的时间复杂度是 O ( n 3 ) O(n^3) O(n3)。而后者枚举回文中心的是 O ( n ) O(n) O(n) 的,对于每个回文中心拓展的次数也是 O ( n ) O(n) O(n)的,所以时间复杂度是 O ( n 2 ) O(n^2) O(n2)。所以我们选择第二种方法来枚举所有的回文子串。
在实现的时候,我们需要处理一个问题,即如何有序地枚举所有可能的回文中心,我们需要考虑回文长度是奇数和回文长度是偶数的两种情况。如果回文长度是奇数,那么回文中心是一个字符;如果回文长度是偶数,那么中心是两个字符。
class Solution:def countSubstrings(self, s: str) -> int:n = len(s)ans = 0for i in range(n):#奇数长度ans += 1l, r = i - 1, i + 1while l > -1 and r < n:if s[l] == s[r]:ans += 1else:breakl -= 1r += 1#偶数长度if (i + 1) < n and s[i] == s[i+1]:ans += 1l, r = i - 1, i + 2while l > -1 and r < n:if s[l] == s[r]:ans += 1else:breakl -= 1r += 1return ansif __name__ == '__main__':s = Solution()print(s.countSubstrings("abc"))print(s.countSubstrings("aaa"))
复杂度分析
- 时间复杂度: O ( n 2 ) O(n^2) O(n2)。
- 空间复杂度: O ( 1 ) O(1) O(1)。
复杂度更低的方法参考:https://leetcode.cn/problems/palindromic-substrings/solution/hui-wen-zi-chuan-by-leetcode-solution/
相关文章:

回文子串-中心拓展
给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。 回文字符串 是正着读和倒过来读一样的字符串。 子字符串 是字符串中的由连续字符组成的一个序列。 具有不同开始位置或结束位置的子串,即使是由相同的字符组成,也会被视作不…...

2023.8各大浏览器11家对比:Edge/Chrome/Opera/Firefox/Tor/Vivaldi/Brave,安全性,速度,体积,内存占用
测试环境:全默认设置的情况下,均在全新的系统上进行测试,系统并未进行任何改动,没有杀毒软件,浏览器进程全部在后台,且为小窗模式,小窗分辨率均为浏览器厂商默认缩放大小(变量不唯一)࿰…...
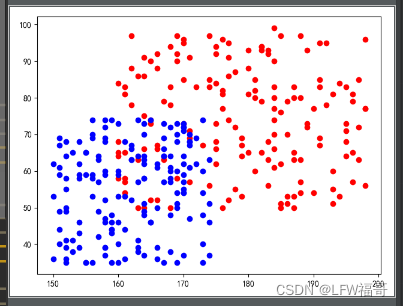
python中的matplotlib画散点图(数据分析与可视化)
python中的matplotlib画散点图(数据分析与可视化) import numpy as np import pandas as pd import matplotlib.pyplot as pltpd.set_option("max_columns",None) plt.rcParams[font.sans-serif][SimHei] plt.rcParams[axes.unicode_minus]Fa…...
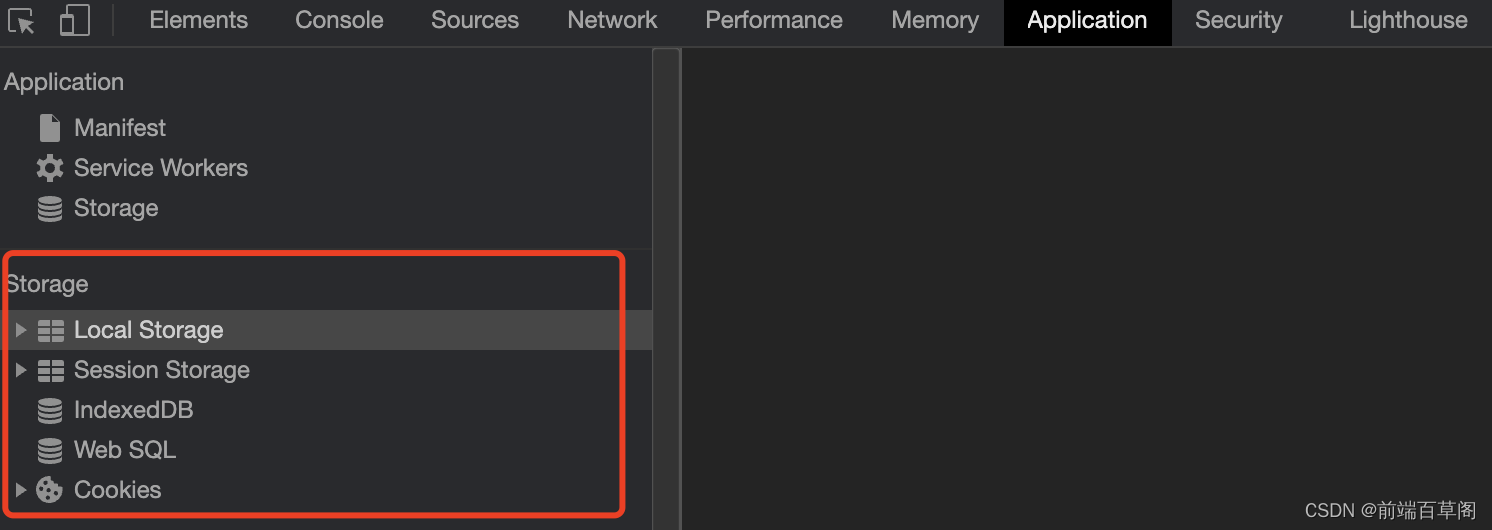
2023前端面试笔记 —— HTML5
系列文章目录 内容链接2023前端面试笔记HTML5 文章目录 系列文章目录前言一、HTML 文件中的 DOCTYPE 是什么作用二、HTML、XML、XHTML 之间有什么区别三、前缀为 data- 开头的元素属性是什么四、谈谈你对 HTML 语义化的理解五、HTML5 对比 HTML4 有哪些不同之处六、meta 标签有…...

【LeetCode】面试题总结 消失的数字 最小k个数
1.消失的数字 两种思路 1.先升序排序,再遍历并且让后一项与前一项比较 2.转化为数学问题求等差数列前n项和 (n的大小为数组的长度),将根据公式求得的应有的和数与数组中实际的和作差 import java.util.*; class Solution {public …...
)
导入功能importExcel (现成直接用)
1. 实体类字段上加 Excel(name "xxx"), 表示要导入的字段 Excel(name "用户名称")private String nickName; 2. controller (post请求) /*** 导入用户数据** param file 文件* param updateSupport 是否更新支持,如果已存在,则进…...

cvc-complex-type.2.4.a: 发现了以元素 ‘base-extension‘ 开头的无效内容。应以 ‘{layoutlib}‘ 之一开头
不能飞的猪只是没用的猪。 —— 宫崎骏 《红猪》 常见的1种case 记录一下,新电脑安装android studio导入公司那些gradle还是5.5左右的工程以后,各种不适应。编译问题出现了。老电脑都是好好的。 cvc-complex-type.2.4.a: 发现了以元素 ‘base-extensi…...

cortex-A7核IIC实验
iic.h: #ifndef __IIC_H__ #define __IIC_H__ #include "stm32mp1xx_gpio.h" #include "stm32mp1xx_rcc.h"/* 通过程序模拟实现I2C总线的时序和协议* GPIOF ---> AHB4* I2C1_SCL ---> PF14* I2C1_SDA ---> PF15** */#define SET_SDA_…...
和 await task.run() 区别 await 运行机制)
task.run()和 await task.run() 区别 await 运行机制
Task.Run() 和 await Task.Run() 都涉及异步编程,但它们在使用场景和效果上有一些区别。1. **Task.Run():**- Task.Run() 是一个用于在后台线程上执行代码块的方法。它将指定的代码块包装在一个新的Task中,并在后台线程上运行。它不会阻塞调用…...

LeetCode面试经典150题(day 2)
26. 删除有序数组中的重复项 难度:简单 给你一个 升序排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。 考虑 nums 的唯…...

阿里云机器学习PAI全新推出特征平台 (Feature Store),助力AI建模场景特征数据高效利用
推荐算法与系统在全球范围内已得到广泛应用,为用户提供了更个性化和智能化的产品推荐体验。在推荐系统领域,AI建模中特征数据的复用、一致性等问题严重影响了建模效率。阿里云机器学习平台 PAI 推出特征平台(PAI-FeatureStore) 。…...

网络安全工具和资源推荐: 介绍网络安全领域中常用的工具、框架、资源和学习资料
章节1: 前言 随着数字化时代的不断深入,网络安全的重要性愈发凸显。在这个信息爆炸的时代,我们必须保护个人隐私、敏感数据以及网络基础设施免受各种威胁。本文将为您介绍一些网络安全领域中常用的工具、框架、资源和学习资料,帮助您更好地入…...

『C语言入门』探索C语言函数
文章目录 导言一、函数概述定义与作用重要性 二、函数分类库函数自定义函数定义使用好处 三、函数参数实际参数(实参)形式参数(形参)内存分配 四、函数调用传值调用传址调用 五、函数嵌套调用与链式访问嵌套调用链式访问 六、函数…...
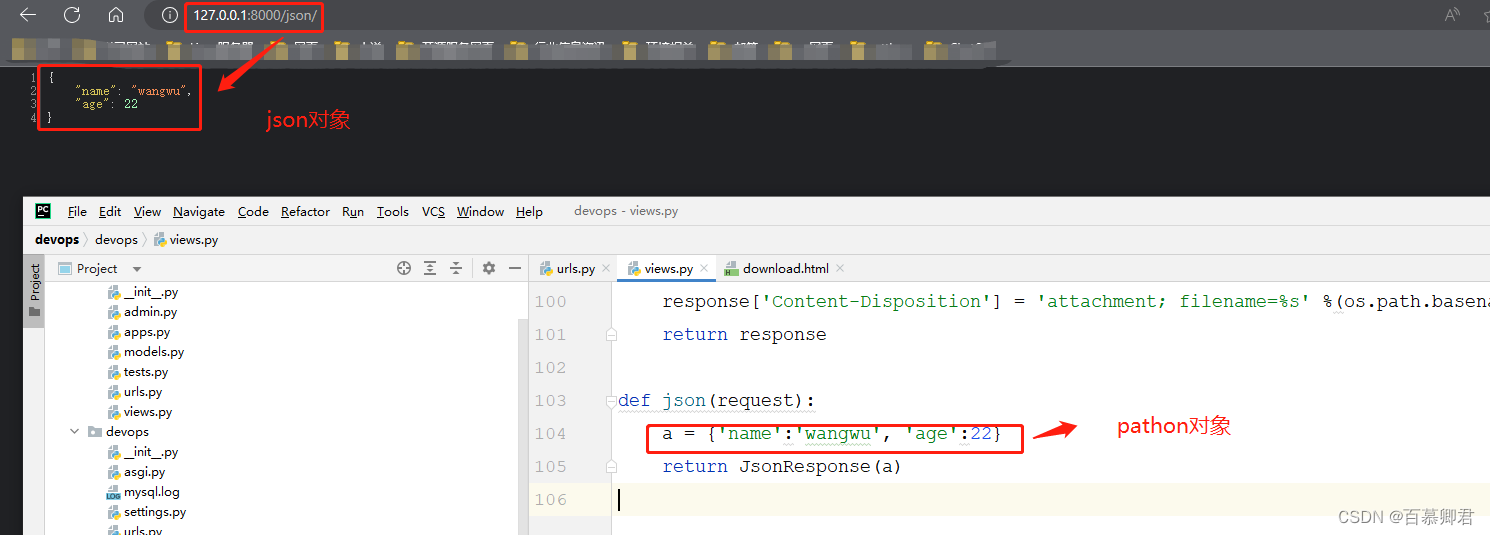
Django基础3——视图函数
文章目录 一、基本了解1.1 Django内置函数1.2 http请求流程 二、HttpRequest对象(接受客户端请求)2.1 常用属性2.2 常用方法2.3 服务端接收URL参数2.4 QueryDict对象2.5 案例2.5.1 表单GET提交2.5.2 表单POST提交2.5.3 上传文件 三、HttpResponse对象&am…...

python 基础篇 day 4 选择结构—— if 结构
文章目录 if 基础结构单 if 语句if-else 语句if-elif-else 语句嵌套的 if 语句 if 进阶用法使用比较运算符使用逻辑运算符使用 in 关键字range() 函数使用 is 关键字使用 pass 语句 三目运算符语法例子注意补充举例注意 if 基础结构 单 if 语句 if 条件: 执行条件为真时的代码…...

科技赋能,教育革新——大步迈向体育强国梦
在 "全民健身"、"体育强国建设"战略的推进下,体育考试成绩被纳入重要升学考试且分值不断提高,体育科目的地位逐步上升到前所未有的高度,在此趋势下,体育教学正演变出更多元化、个性化的需求。然而现实中却面临…...

【秋招基础】后端开发——笔面试常见题目
综述: 💞目的:本系列是个人整理为了秋招算法的,整理期间苛求每个知识点,平衡理解简易度与深入程度。 🥰来源:材料主要源于网上知识点进行的,每个代码参考热门博客和GPT3.5࿰…...
自定义loadbalance实现feignclient的自定义路由
自定义loadbalance实现feignclient的自定义路由 项目背景 服务A有多个同事同时开发,每个同事都在dev或者test环境发布自己的代码,注册到注册中心有好几个(本文nacos为例),这时候调用feign可能会导致请求到不同分支的服务上面,会…...
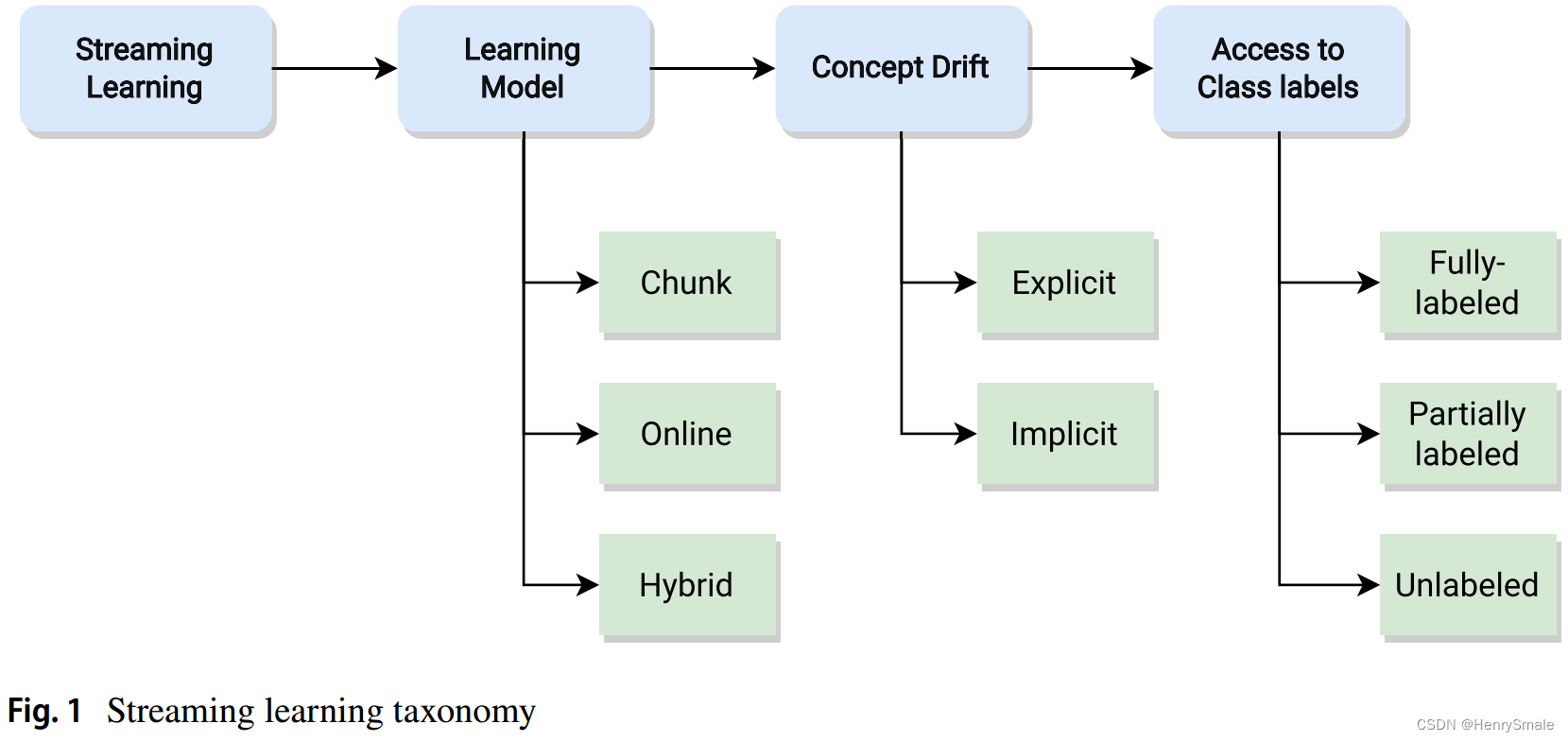
论文笔记:从不平衡数据流中学习的综述: 分类、挑战、实证研究和可重复的实验框架
0 摘要 论文:A survey on learning from imbalanced data streams: taxonomy, challenges, empirical study, and reproducible experimental framework 发表:2023年发表在Machine Learning上。 源代码:https://github.com/canoalberto/imba…...

C#设计模式六大原则之--迪米特法则
设计模式六大原则是单一职责原则、里氏替换原则、依赖倒置原则、接口隔离原则、迪米特法则、开闭原则。它们不是要我们刻板的遵守,而是根据实际需要灵活运用。只要对它们的遵守程度在一个合理的范围内,努为做到一个良好的设计。本文主要介绍一下.NET(C#)…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

生成 Git SSH 证书
🔑 1. 生成 SSH 密钥对 在终端(Windows 使用 Git Bash,Mac/Linux 使用 Terminal)执行命令: ssh-keygen -t rsa -b 4096 -C "your_emailexample.com" 参数说明: -t rsa&#x…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

有限自动机到正规文法转换器v1.0
1 项目简介 这是一个功能强大的有限自动机(Finite Automaton, FA)到正规文法(Regular Grammar)转换器,它配备了一个直观且完整的图形用户界面,使用户能够轻松地进行操作和观察。该程序基于编译原理中的经典…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

怎么让Comfyui导出的图像不包含工作流信息,
为了数据安全,让Comfyui导出的图像不包含工作流信息,导出的图像就不会拖到comfyui中加载出来工作流。 ComfyUI的目录下node.py 直接移除 pnginfo(推荐) 在 save_images 方法中,删除或注释掉所有与 metadata …...

深入浅出Diffusion模型:从原理到实践的全方位教程
I. 引言:生成式AI的黎明 – Diffusion模型是什么? 近年来,生成式人工智能(Generative AI)领域取得了爆炸性的进展,模型能够根据简单的文本提示创作出逼真的图像、连贯的文本,乃至更多令人惊叹的…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...
