26. 删除有序数组中的重复项(简单系列)
给你一个 升序排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。
考虑 nums 的唯一元素的数量为 k ,你需要做以下事情确保你的题解可以被通过:
更改数组 nums ,使 nums 的前 k 个元素包含唯一元素,并按照它们最初在 nums 中出现的顺序排列。nums 的其余元素与 nums 的大小不重要。
返回 k 。
判题标准:
系统会用下面的代码来测试你的题解:
int[] nums = […]; // 输入数组
int[] expectedNums = […]; // 长度正确的期望答案
int k = removeDuplicates(nums); // 调用
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums[i] == expectedNums[i];
}
如果所有断言都通过,那么您的题解将被 通过。
示例 1:
输入:nums = [1,1,2]
输出:2, nums = [1,2,_]
解释:函数应该返回新的长度 2 ,并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。
示例 2:
输入:nums = [0,0,1,1,1,2,2,3,3,4]
输出:5, nums = [0,1,2,3,4]
解释:函数应该返回新的长度 5 , 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。
提示:
1 <= nums.length <= 3 * 104
-104 <= nums[i] <= 104
nums 已按 升序 排列
第一种:
public int removeDuplicates(int[] nums) {
//获取数组 nums 的长度,如果长度为0,直接返回0,因为数组中没有重复元素int n = nums.length;if (n== 0){return 0;}
//定义两个指针 fast 和 slow,初始值都为1。int fast =1;int slow =1;
//通过遍历数组,比较 fast 指针和 fast-1 指针对应的元素是否相等。
//如果不相等,说明找到了一个新的不重复元素,将其赋值给 slow 指针对应的位置,并将 slow 指针向前移动一位。
//无论相等与否,fast 指针都应向前移动一位。while(fast<n){if(nums[fast] != nums[fast-1]){nums[slow]= nums[fast];++slow; }++fast;}//返回 slow 的值,即去除重复元素后数组的长度。return slow;
}
第二种方式
public int removeDuplicates(int[] nums) {
//获取数组 nums 的长度,如果长度为0,直接返回0,因为数组中没有重复元素int n = nums.length;if (n== 0){return 0;}int p =0; //初始化指针p为0int q =1; // 初始化指针q为1while(q<n){ // 当指针q小于n时执行循环if(nums[p] != nums[q]){ // 如果nums中指针p和指针q的元素不相等nums[p+1] =nums[q]; // 将nums中指针q的元素赋值给指针p+1的位置++p; // 指针p向右移动一位}++q; // 指针q向右移动一位}return p+1; // 返回最终不重复的元素的个数
}
相关文章:
)
26. 删除有序数组中的重复项(简单系列)
给你一个 升序排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。然后返回 nums 中唯一元素的个数。 考虑 nums 的唯一元素的数量为 k ,你需要做…...
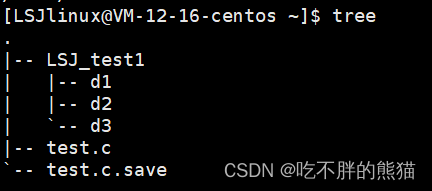
【linux】基本指令(二)【man、echo、cat、cp】
目录 一、man指令二、echo指令三、cat指令二、cp指令一些常见快捷键 一、man指令 Linux的命令有很多参数,我们不可能全记住,可以通过查看联机手册获取帮助。访问Linux手册页的命令是 man 语法: man [选项] 命令 常用选项 1.-k 根据关键字搜索联机帮助 2…...

【视频】Python用LSTM长短期记忆神经网络对不稳定降雨量时间序列进行预测分析|数据分享...
全文下载链接:http://tecdat.cn/?p23544 在本文中,长短期记忆网络——通常称为“LSTM”——是一种特殊的RNN递归神经网络,能够学习长期依赖关系(点击文末“阅读原文”获取完整代码数据)。 本文使用降雨量数据…...
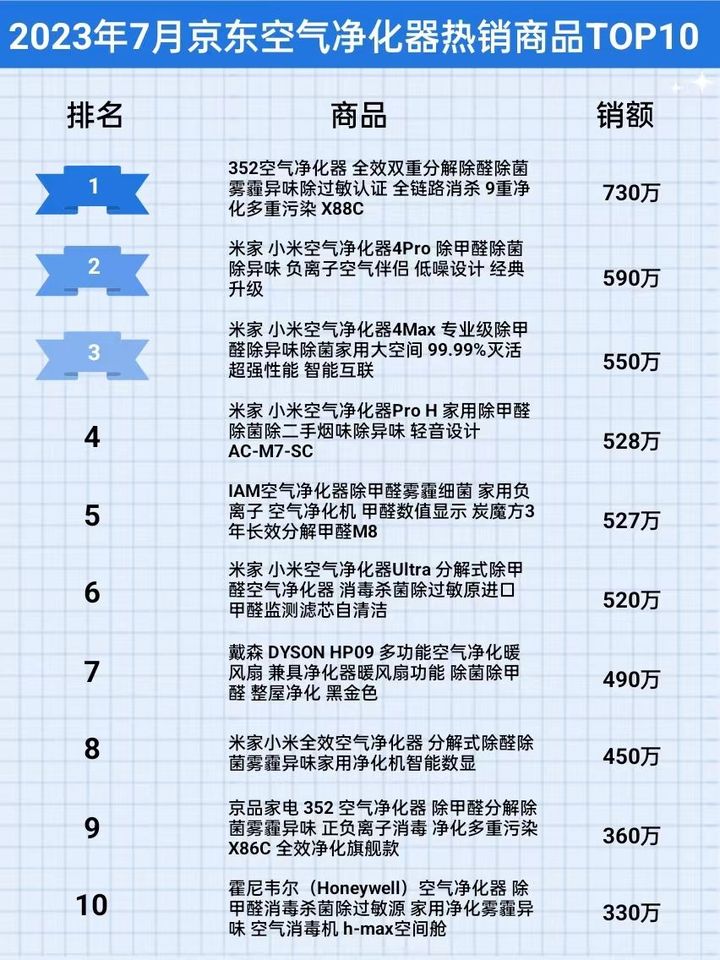
2023年7月京东空气净化器行业品牌销售排行榜(京东运营数据分析)
随着科技发展,智能家具在日常生活中出现的频率越来越高,许多曾经不被关注的家电也出现在其中,包括近年来逐渐兴起的空气净化器。伴随人们对自身健康的重视度越来越高,作为能够杀灭空气污染物、有效提高空气清洁度的产品࿰…...
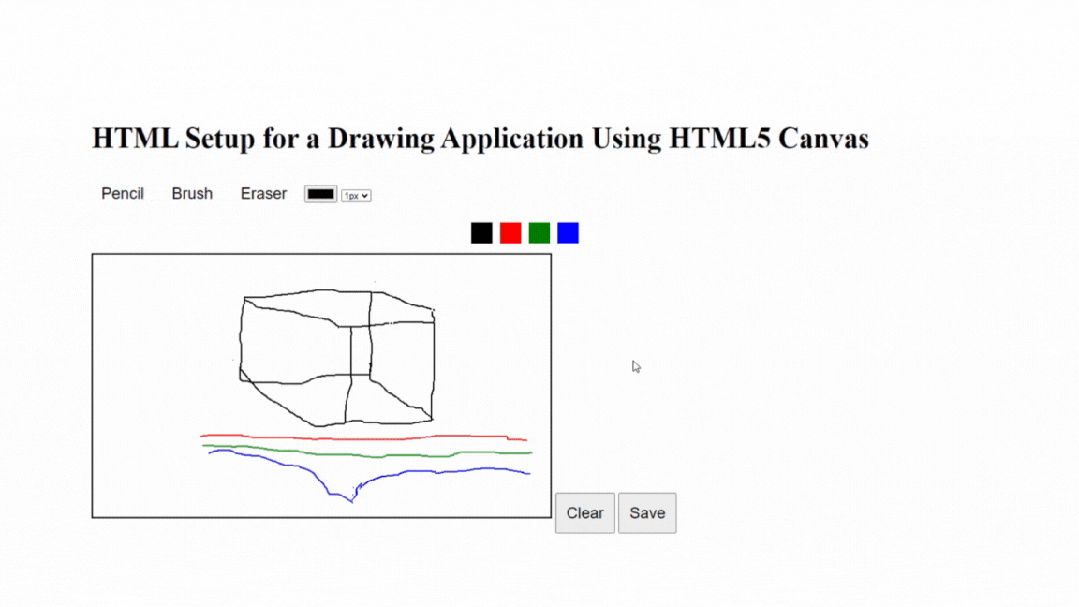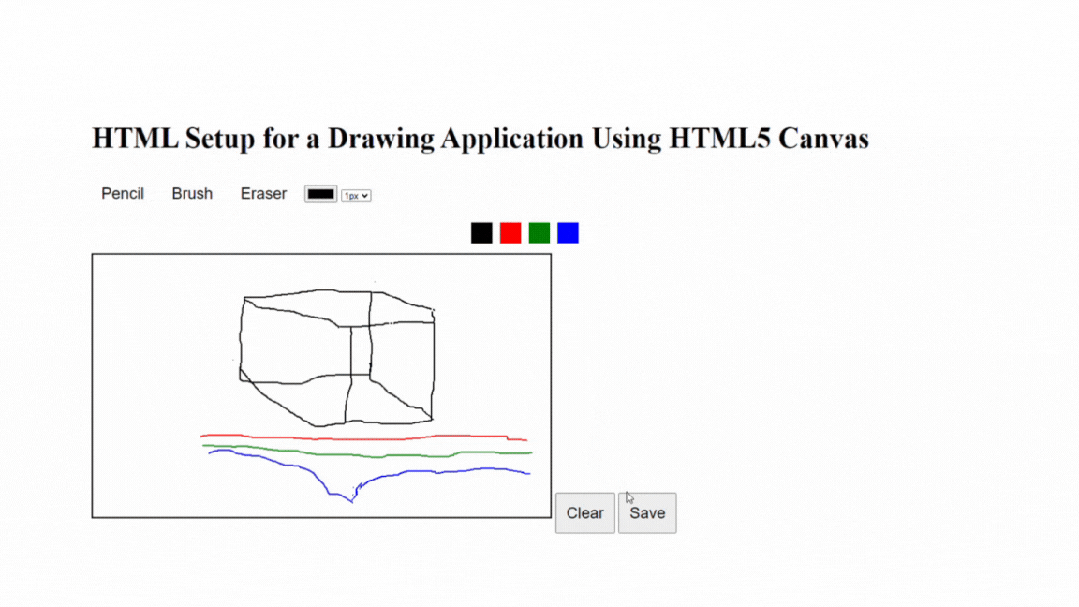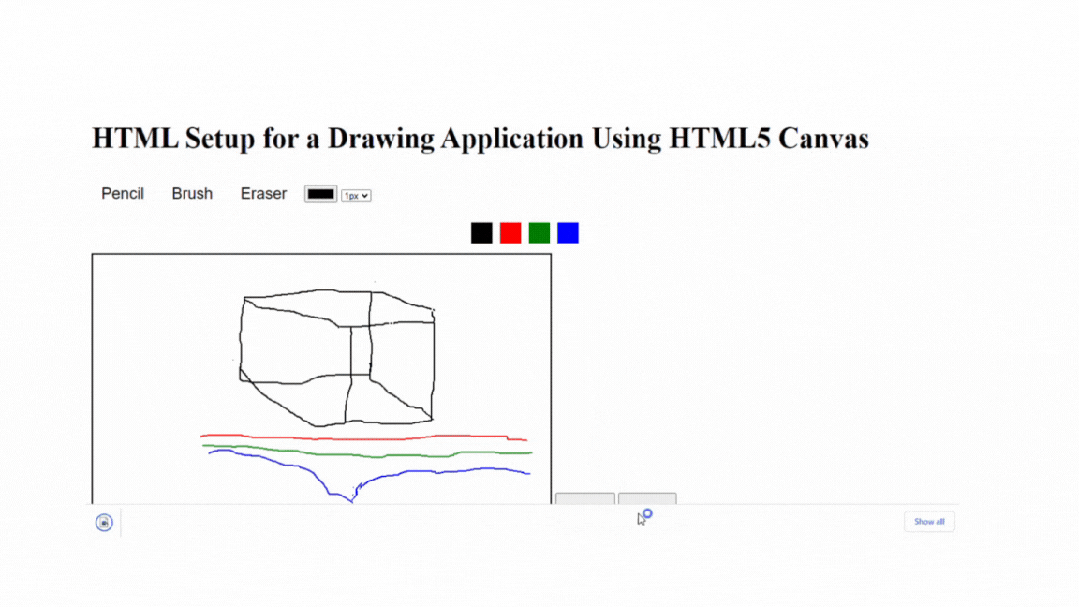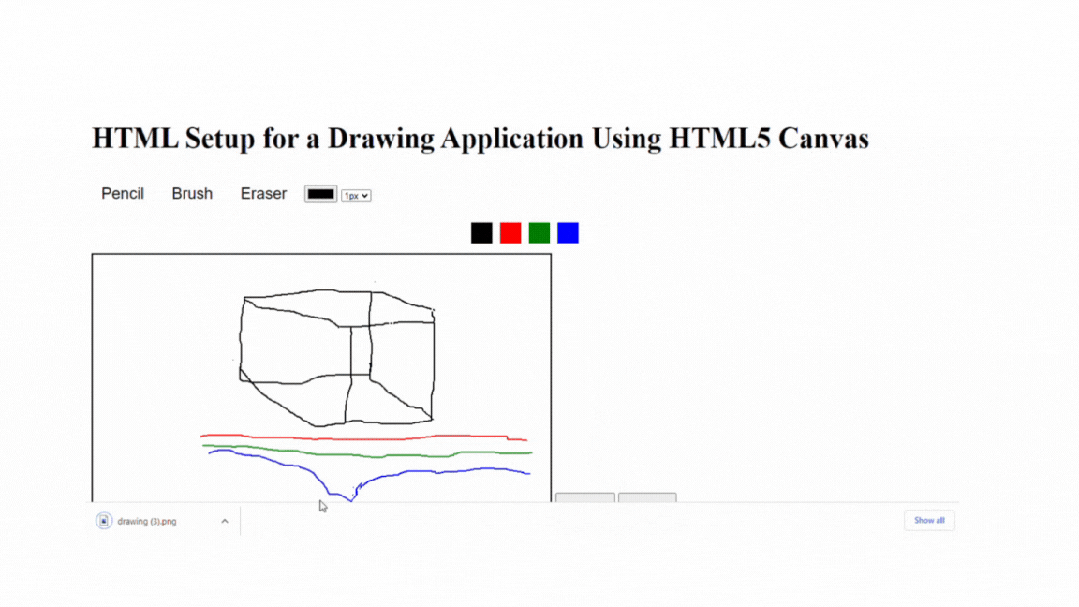
原生小案例:如何使用HTML5 Canvas构建画板应用程序
使用HTML5 Canvas构建绘图应用是在Web浏览器中创建交互式和动态绘图体验的绝佳方式。HTML5 Canvas元素提供了一个绘图表面,允许您操作像素并以编程方式创建各种形状和图形。本文将为您提供使用HTML5 Canvas创建绘图应用的概述和指导。此外,它还将通过解释…...
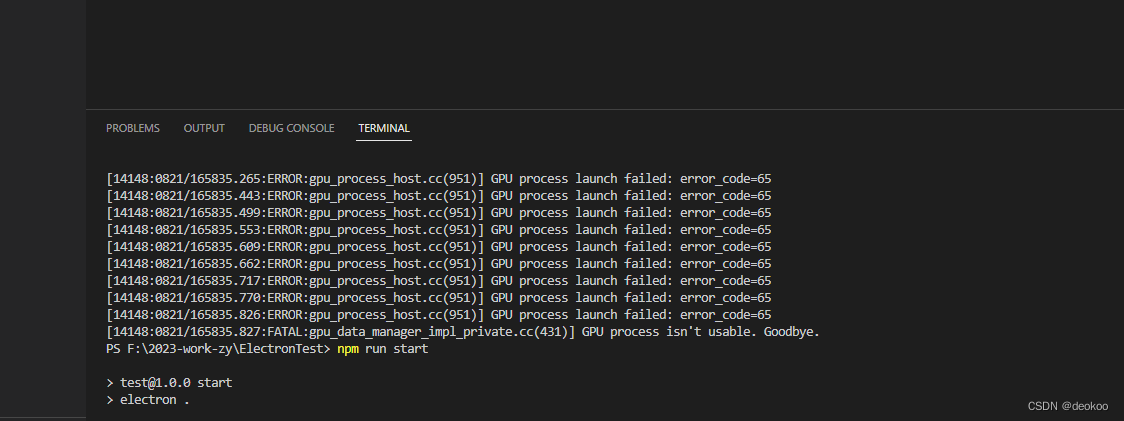
Electron 报gpu_process_host.cc(951)] GPU process launch faile错误
解决方法,在入口js文件中,添加如下代码: app.commandLine.appendSwitch(no-sandbox)...

每天一分享#读up有感#
不知道开头怎么写,想了一下,要不,就这样吧,开头也就写完 今日分享 分享一博主的分享——https://blog.csdn.net/zhangay1998/article/details/121736687 全程高能,大佬就diao,一鸣惊人、才能卓越、名扬四…...

threejs贴图系列(一)canvas贴图
threejs不仅支持各种texture的导入生成贴图,还可以利用canvas绘制图片作为贴图。这就用到了CanvasTexture,它接受一个canas对象。只要我们绘制好canvas,就可以作为贴图了。这里我们利用一张图片来实现这个效果。 基础代码: impo…...
taro react/vue h5 中的上传input onchange 值得区别
<inputclassNamebase-input-file-h5typefileacceptimage/*capturecameraonChange{onChangeInput} />1、taro3react 2、taro3vue3...
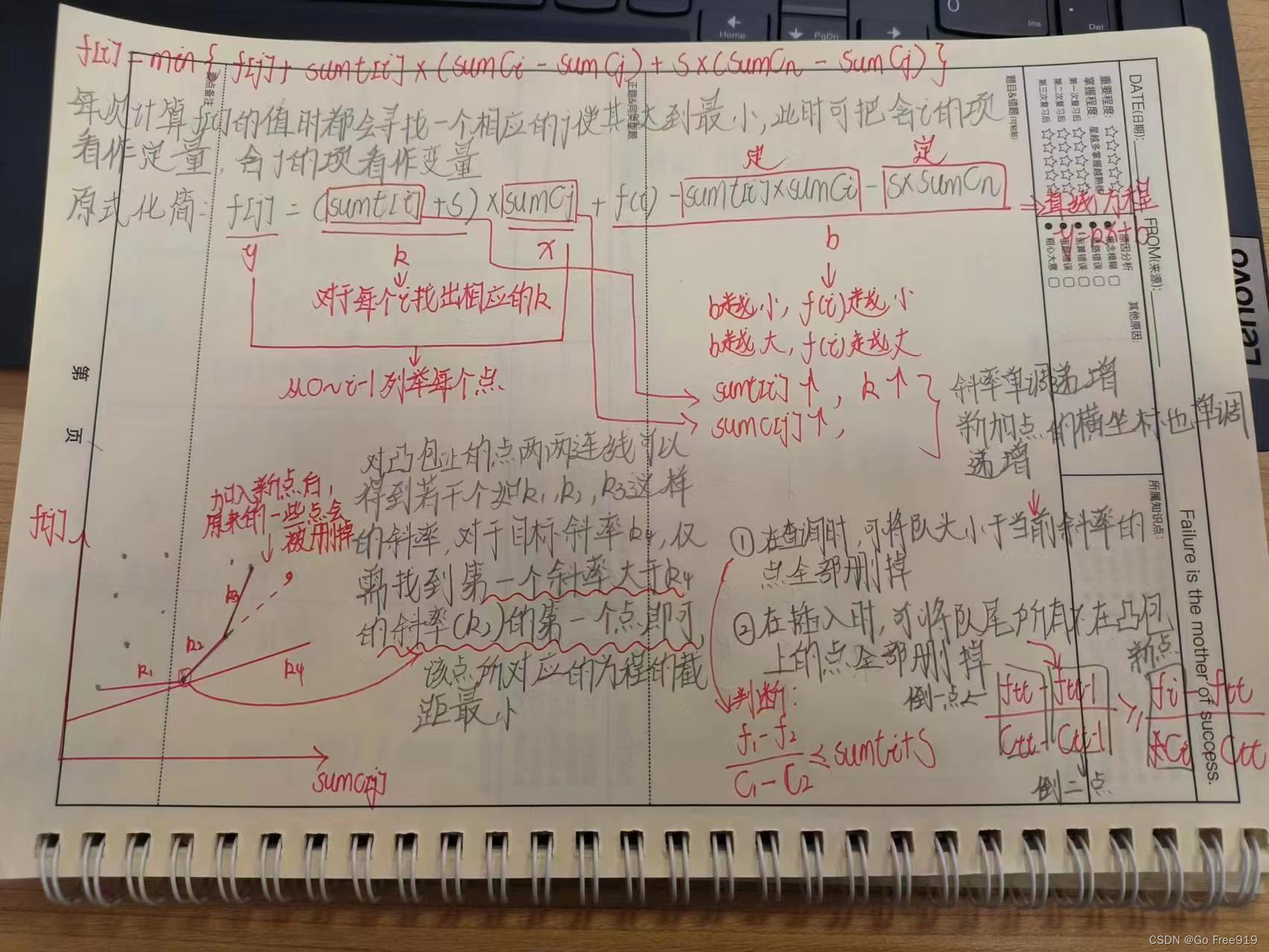
(AcWing) 任务安排(I,II,III)
任务安排I: 有 N 个任务排成一个序列在一台机器上等待执行,它们的顺序不得改变。 机器会把这 N 个任务分成若干批,每一批包含连续的若干个任务。 从时刻 0 开始,任务被分批加工,执行第 i 个任务所需的时间是 Ti。 另外&#x…...

Excel筛选后复制粘贴不连续问题的解决
一直以来都没好好正视这个问题认真寻求解决办法 终于还是被需求逼出来了,懒人拯救世界[doge] 一共找到两个方法,个人比较喜欢第二种,用起来很方便 Way1:CtrlG定位可见单元格后使用vlookup解决(感觉不定位直接公式向下…...

【SCSS变量】$ | | var | @for | @include | @function | @each 等常用方法使用
SCSS优点:编写清晰、无冗余、语义化的CSS,减少不必要的重复工作 1、变量声明($)和使用2、使用 & 代替父元素3、在HTML中使用 :style{--name: 动态值}自定义属性,在SCSS中用var(--name)函数绑定动态变量值ÿ…...

iOS 17 及 Xcode 15.0 Beta7 问题记录
1、iOS 17 真机调试问题 iOS 17之后,真机调试Beta版本必须使用Beta版本的Xcode来调试,用以前复制DeviceSupport 方式无法调试,新的Beta版本Xcode中,已经不包含 iOS 17目录。如下图: 解决方案: 1&#x…...
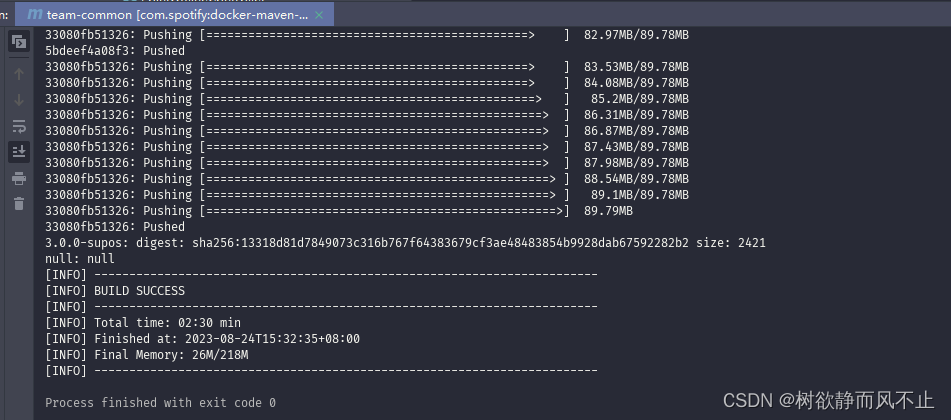
docker-maven-plugin直接把镜像推到私有仓库
接着上篇 推送到本地docker 我们已经把服务做成镜像推到docker,也可以通过docker login 私有地址,去push。麻烦 直接上代码 1、pom改动 <properties><docker.registry>eco-registry.XXX.com</docker.repostory><docker.registry…...

2023年机器学习项目—布匹缺陷检测
2023年机器学习项目———布匹缺陷检测 测试环境: CPU : 12th Gen Intel Core™ i7-12700H 2.70 GHz GPU : NVIDIA RTX3070Ti RAM : 32GB Matlab R2020a (Deep Learning Tools) 注 :Data文件过大 未上传 一.神经网络概述 1. 卷积神经网络概念 人工神经网络(Artific…...
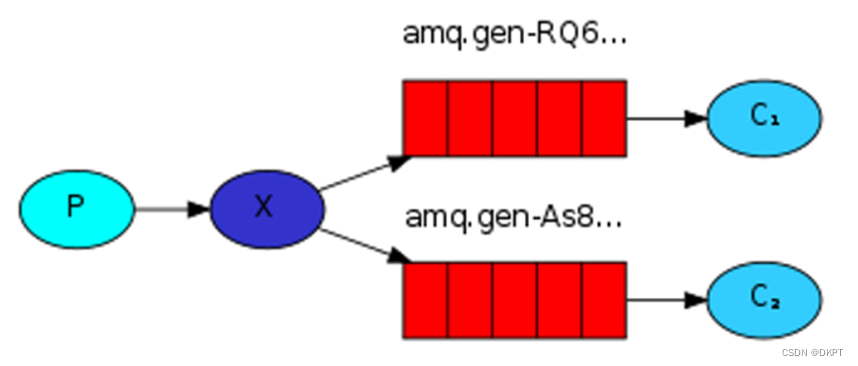
RabbitMQ---订阅模型分类
订阅模型分类 在之前的模式中,我们创建了一个工作队列。 工作队列背后的假设是:每个任务只被传递给一个工作人员。 在这一部分,我们将做一些完全不同的事情 - 我们将会传递一个信息给多个消费者。 这种模式被称为“发布/订阅”。 订阅模型示意…...
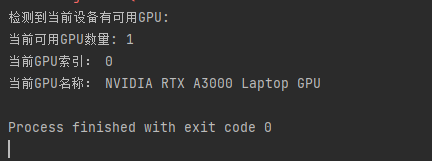
pycharm添加虚拟环境以及虚拟环境安装pytorch
file、settings、interpreter、add interpreter、add local interpreter 记住不要勾选inherit,不然会把主环境的东西继承到虚拟环境。 创建前可以先点existing看看有没有已经建好的虚拟环境 有的时候pycharm有问题,创建了虚拟环境没有显示。找一个.py文…...

Git企业开发控制理论和实操-从入门到深入(三)|分支管理
前言 那么这里博主先安利一些干货满满的专栏了! 首先是博主的高质量博客的汇总,这个专栏里面的博客,都是博主最最用心写的一部分,干货满满,希望对大家有帮助。 高质量博客汇总 然后就是博主最近最花时间的一个专栏…...
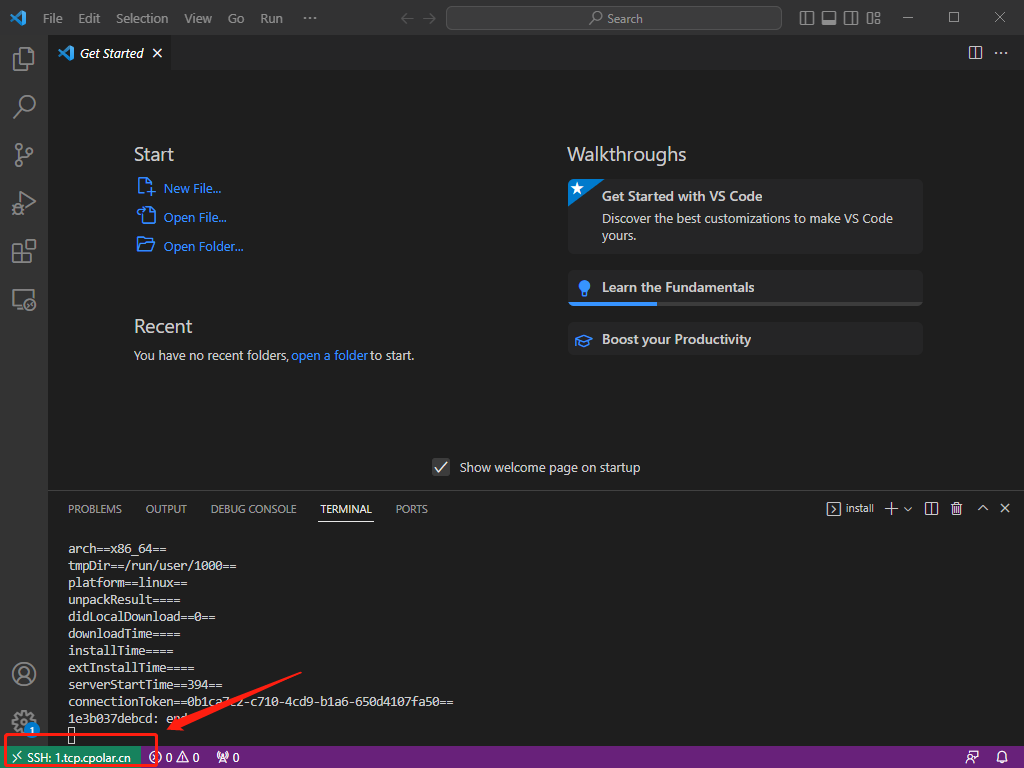
【VsCode】SSH远程连接Linux服务器开发,搭配cpolar内网穿透实现公网访问(1)
文章目录 前言1、安装OpenSSH2、vscode配置ssh3. 局域网测试连接远程服务器4. 公网远程连接4.1 ubuntu安装cpolar内网穿透4.2 创建隧道映射4.3 测试公网远程连接 5. 配置固定TCP端口地址5.1 保留一个固定TCP端口地址5.2 配置固定TCP端口地址5.3 测试固定公网地址远程 前言 远程…...
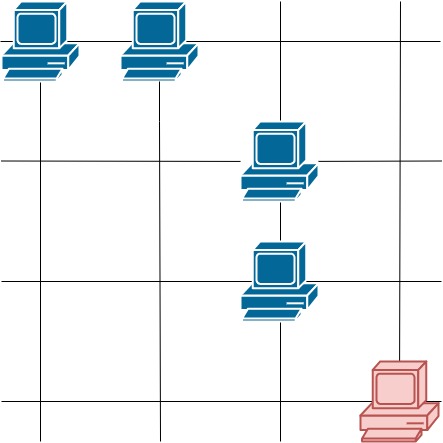
LC-1267. 统计参与通信的服务器(枚举 + 计数)
1267. 统计参与通信的服务器 中等 这里有一幅服务器分布图,服务器的位置标识在 m * n 的整数矩阵网格 grid 中,1 表示单元格上有服务器,0 表示没有。 如果两台服务器位于同一行或者同一列,我们就认为它们之间可以进行通信。 请…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

听写流程自动化实践,轻量级教育辅助
随着智能教育工具的发展,越来越多的传统学习方式正在被数字化、自动化所优化。听写作为语文、英语等学科中重要的基础训练形式,也迎来了更高效的解决方案。 这是一款轻量但功能强大的听写辅助工具。它是基于本地词库与可选在线语音引擎构建,…...

以光量子为例,详解量子获取方式
光量子技术获取量子比特可在室温下进行。该方式有望通过与名为硅光子学(silicon photonics)的光波导(optical waveguide)芯片制造技术和光纤等光通信技术相结合来实现量子计算机。量子力学中,光既是波又是粒子。光子本…...

代码随想录刷题day30
1、零钱兑换II 给你一个整数数组 coins 表示不同面额的硬币,另给一个整数 amount 表示总金额。 请你计算并返回可以凑成总金额的硬币组合数。如果任何硬币组合都无法凑出总金额,返回 0 。 假设每一种面额的硬币有无限个。 题目数据保证结果符合 32 位带…...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

JS手写代码篇----使用Promise封装AJAX请求
15、使用Promise封装AJAX请求 promise就有reject和resolve了,就不必写成功和失败的回调函数了 const BASEURL ./手写ajax/test.jsonfunction promiseAjax() {return new Promise((resolve, reject) > {const xhr new XMLHttpRequest();xhr.open("get&quo…...
