猜数字大小 II
力扣链接
力扣
题目描述:
我们正在玩一个猜数游戏,游戏规则如下:
- 我从
1到n之间选择一个数字。 - 你来猜我选了哪个数字。
- 如果你猜到正确的数字,就会 赢得游戏 。
- 如果你猜错了,那么我会告诉你,我选的数字比你的 更大或者更小 ,并且你需要继续猜数。
- 每当你猜了数字
x并且猜错了的时候,你需要支付金额为x的现金。如果你花光了钱,就会 输掉游戏 。
给你一个特定的数字 n ,返回能够 确保你获胜 的最小现金数,不管我选择那个数字 。
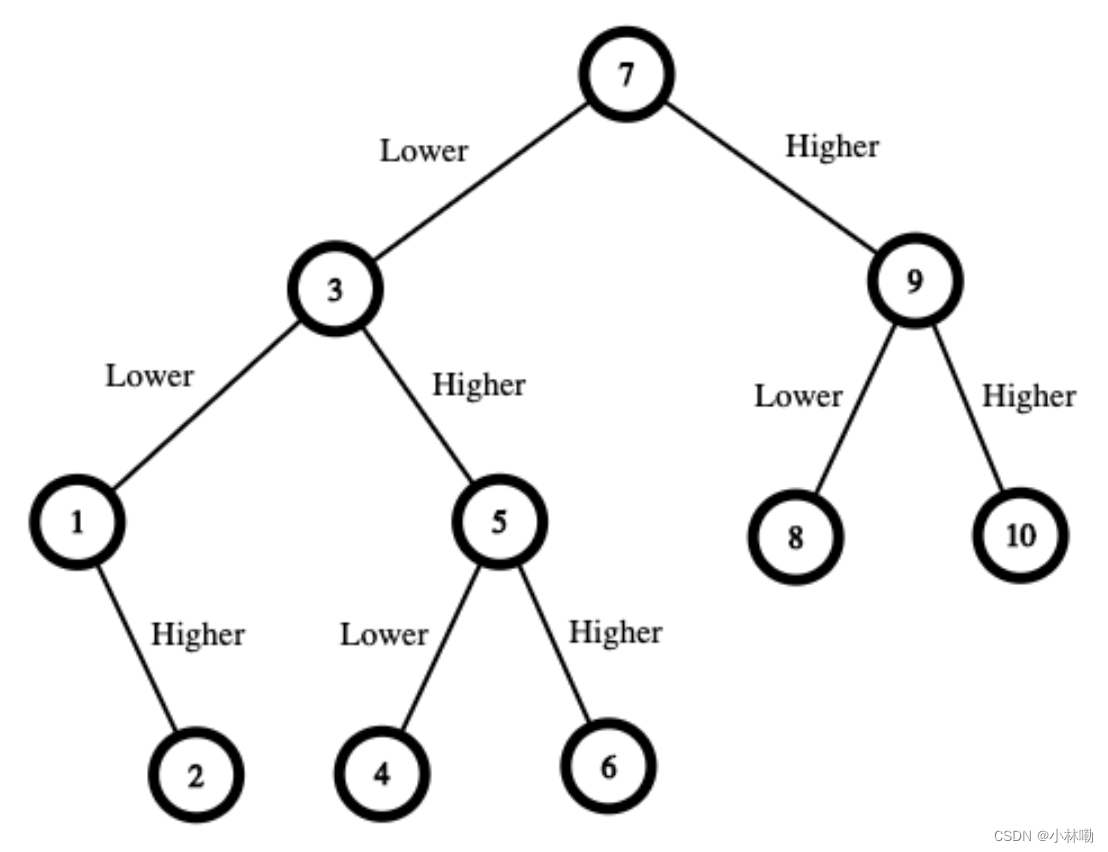
输入:n = 10 输出:16 解释:制胜策略如下: - 数字范围是 [1,10] 。你先猜测数字为 7 。- 如果这是我选中的数字,你的总费用为 $0 。否则,你需要支付 $7 。- 如果我的数字更大,则下一步需要猜测的数字范围是 [8,10] 。你可以猜测数字为 9 。- 如果这是我选中的数字,你的总费用为 $7 。否则,你需要支付 $9 。- 如果我的数字更大,那么这个数字一定是 10 。你猜测数字为 10 并赢得游戏,总费用为 $7 + $9 = $16 。- 如果我的数字更小,那么这个数字一定是 8 。你猜测数字为 8 并赢得游戏,总费用为 $7 + $9 = $16 。- 如果我的数字更小,则下一步需要猜测的数字范围是 [1,6] 。你可以猜测数字为 3 。- 如果这是我选中的数字,你的总费用为 $7 。否则,你需要支付 $3 。- 如果我的数字更大,则下一步需要猜测的数字范围是 [4,6] 。你可以猜测数字为 5 。- 如果这是我选中的数字,你的总费用为 $7 + $3 = $10 。否则,你需要支付 $5 。- 如果我的数字更大,那么这个数字一定是 6 。你猜测数字为 6 并赢得游戏,总费用为 $7 + $3 + $5 = $15 。- 如果我的数字更小,那么这个数字一定是 4 。你猜测数字为 4 并赢得游戏,总费用为 $7 + $3 + $5 = $15 。- 如果我的数字更小,则下一步需要猜测的数字范围是 [1,2] 。你可以猜测数字为 1 。- 如果这是我选中的数字,你的总费用为 $7 + $3 = $10 。否则,你需要支付 $1 。- 如果我的数字更大,那么这个数字一定是 2 。你猜测数字为 2 并赢得游戏,总费用为 $7 + $3 + $1 = $11 。 在最糟糕的情况下,你需要支付 $16 。因此,你只需要 $16 就可以确保自己赢得游戏。
解法:
1.记忆化递归:
简单地思路梳理:
我们可以枚举1到n中的每一个数字,记为x,那么分为两种情况,猜中了和没猜中
- 假如 x 正好是选中的数,那么,付出的代价为 0;
- 假如 x 不是选中的数,那么,付出的代价为 x,然后,我们会得到提示,选中的数比 x 大还是比 x 小:
- 假如比 x 小,我们只要求得 1 到 x-1 的最小代价,再加上 x 就能得到猜 x 时的最小代价;
- 假如比 x 大,我们只要求得 x+1 到 n 的最小代价,再加上 x 就能得到猜 x 时的最小代价;
- 而选中的数有可能在 x 的左边,也可能在 x 的右边,为了保证我们能够赢得游戏,我们需要备用的现金应该是左右两边的最小代价的最大值再加上 x 本身。
当我们枚举完这些 x 后,取其中的最小值就是我们需要备用的现金。
所以,我们可以得到递推公式:
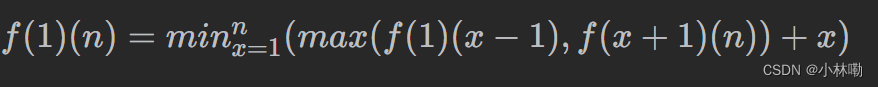 你会发现存在很多重复的计算,比如,计算 f(1)(4) 的时候会计算 f(1)(2) 和 f(1)(3),而计算 f(1)(3) 的时候也会计算 f(1)(2),所以,我们可以加上缓存记录已经计算过的数值,这就是记忆化搜索
你会发现存在很多重复的计算,比如,计算 f(1)(4) 的时候会计算 f(1)(2) 和 f(1)(3),而计算 f(1)(3) 的时候也会计算 f(1)(2),所以,我们可以加上缓存记录已经计算过的数值,这就是记忆化搜索
class Solution {public int getMoneyAmount(int n) {int[][] memo = new int[n + 2][n + 2];return dfs(1, n, memo);}private int dfs(int start, int end, int[][] memo) {if (start >= end) {return 0;}if (memo[start][end] != 0) {return memo[start][end];}int ans = Integer.MAX_VALUE;for (int k = start; k <= end; k++) {ans = Math.min(ans, Math.max(dfs(start, k - 1, memo), dfs(k + 1, end, memo)) + k);}return memo[start][end] = ans;}
}2.动规(区间DP):
再上一步的记忆化递归中,我们发现,每次计算区间[x,y]都依赖与更小的区间,那么调整区间的计算顺序,我们不妨先计算小的区间,这样在计算大的区间的时候就不必重新计算小的区间了。
- 状态定义:dp[i][j]表示选中的数在 [i,j] 之间时能够确保获胜需要备用的现金数;
- 状态转移:dp[i][j]=min{k=i->j}(max(dp[i][k-1], dp[i][k+1]) + k);
- 初始值:对于只有一个数时,选中的数肯定就是这个数,代价为0,所以,初始值为 dp[i][i] = 0,Java中不需要特殊处理;
- 返回值:dp[1][n];
典型的区间dp的写法:
枚举长度从小到大:
class Solution {public int getMoneyAmount(int n) {// dp[i][j]表示选择的数在[i,j]之间时能够确保获胜的最小钱数// dp[i][j]=min{k=i->j}(max(dp[i][k-1], dp[i][k+1]) + k)int[][] dp = new int[n + 2][n + 2];for (int len = 2; len <= n; len++) {//长度从小到大枚举for (int i = 1; i <= n - len + 1; i++) {//从小到大,也就是举例 [1,1+len] [2,2+len]这样int j = i + len - 1;int min = Integer.MAX_VALUE;for (int k = i; k <= j; k++) {//注意k在后面的整体之中,为什么加k,因为是没选中k,所以要付出代价为k//然后比较原来的数据和当前没选中需要花费的最大的代价,取最大代价中最小的min = Math.min(min, Math.max(dp[i][k - 1], dp[k + 1][j]) + k);}dp[i][j] = min;}}return dp[1][n];}
}代码说明:
注意,for循环中的len是我们枚举的长度,不是整个数字n的长度。
相关文章:
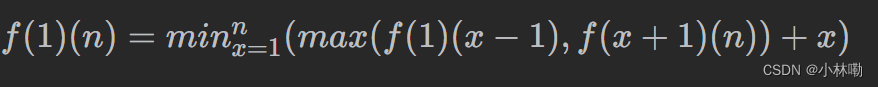
猜数字大小 II
力扣链接 力扣 题目描述: 我们正在玩一个猜数游戏,游戏规则如下: 我从 1 到 n 之间选择一个数字。你来猜我选了哪个数字。如果你猜到正确的数字,就会 赢得游戏 。如果你猜错了,那么我会告诉你,我选的数…...

CCNP350-401学习笔记(251-300题)
251、 Which IPv6 OSPF network type is applied to interface Fa0/0 of R2 by default? A. multipointB. broadcast C. Ethernet D. point-to-point 252、Which EIGRP feature allows the use of leak maps? A. neighborB. Stub C. offset-list D. address-family 253、W…...
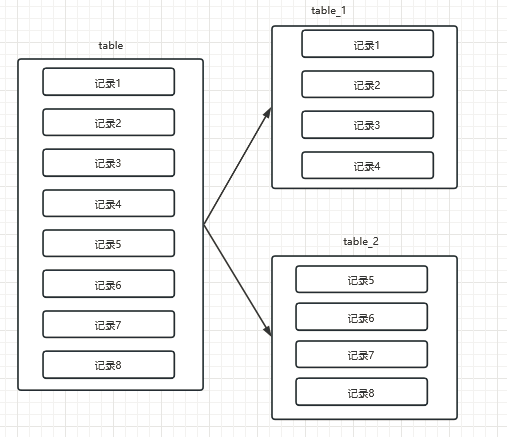
掌握MySQL分库分表(二)Mysql数据库垂直分库分表、水平分库分表
文章目录垂直分表拆分方法举例垂直分库水平分表水平分库小结垂直角度(表结构不一样)水平角度(表结构一样)垂直分表 需求:商品表字段太多,每个字段访问频次不⼀样,浪费了IO资源,需要…...
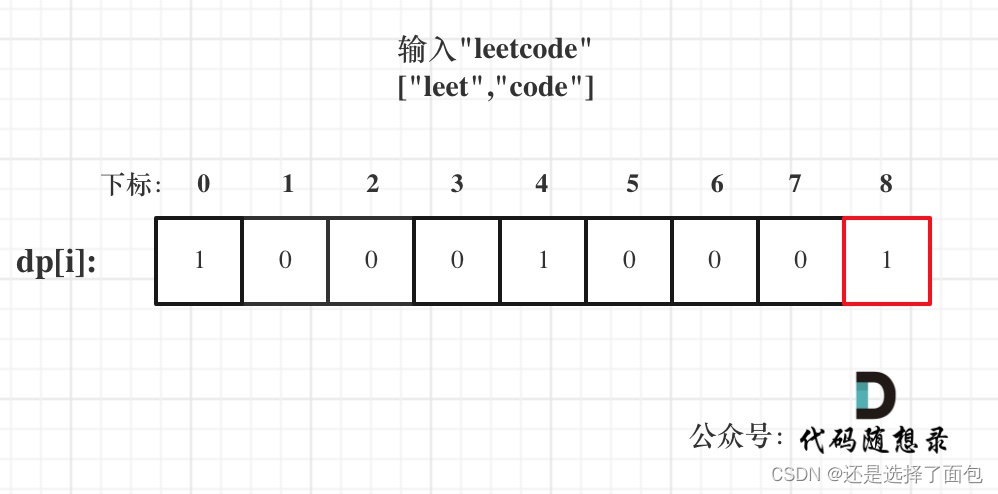
算法训练营 day50 动态规划 单词拆分 多重背包理论基础
算法训练营 day50 动态规划 单词拆分 多重背包理论基础 单词拆分 139. 单词拆分 - 力扣(LeetCode) 给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。 注意:不要求字典中出现的单词…...

一文3000字用Postman从0到1实现UI自动化测试
“阅读本文大概需要4分钟。Postman不是做接口测试的吗?为什么还能做UI自动化测试呢? 其实,只要你了解Selenium的运行原理,就可以理解为什么Postman也能实现UI自动化测试了。 Selenium底层原理 运行代码,启动浏览器后…...
)
2023年美国大学生数学建模C题:预测Wordle结果建模详解+模型代码(一)
目录 前言 一、题目理解 背景 解析 字段含义: 建模要求 二、建模思路...
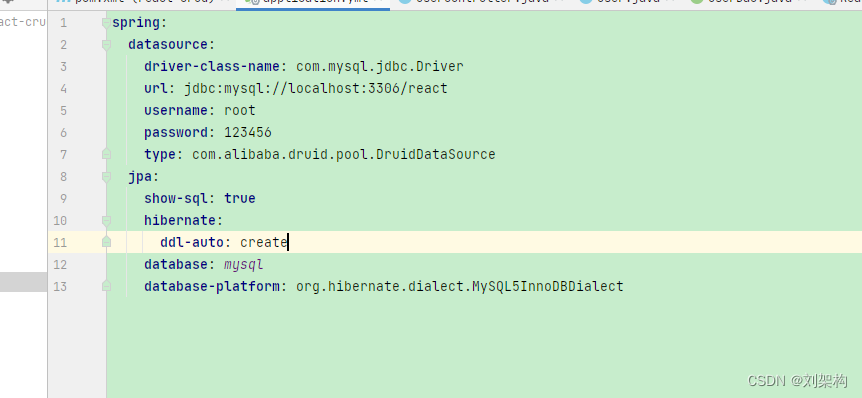
spring-boot 整合 前端框架 React 增删改查(附源码)
看了很多 关于 SpringBoot 增删改查 的文章 ,但是 React 前端框架这块似乎没什么人玩,一般都是Vue进行整合 ,所以想写一篇关于 React 整合 SpringBoot 增删改查的项目 React 学习区域 React中文教程: https://www.php.cn/doc/react/tutorial/…...

未来的城市:智慧城市定义、特征、应用、场景
智慧城市是通过连接一个地区的物理、经济和社会基础设施,以创新、有效和高效的方式应用和实施技术来发展城市的概念,以改善服务并实现更好的生活质量。智慧城市是一个将信息和通信技术融入日常治理的城市区域,旨在实现效率、改善公共服务、增…...
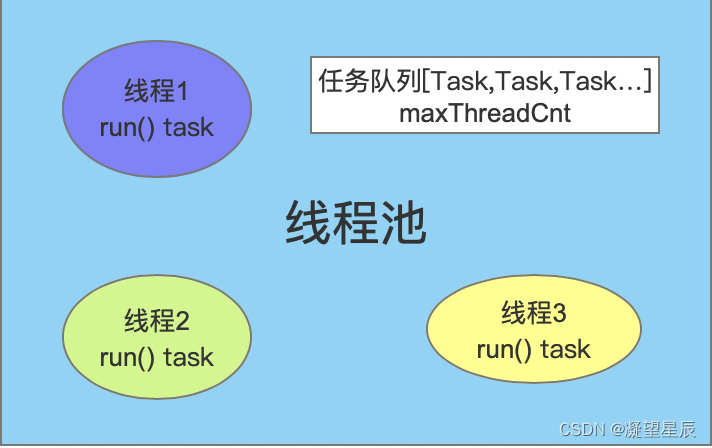
Qt线程池QThreadPool使用示例
目录前言1.线程池原理介绍2.QThreadPool详细介绍反复执行同一个任务设置线程过期时间线程数量信息3.QThreadPool示例4.总结前言 线程池顾名思义就是同时管理多个线程的"池子",它是一种并发处理技术,在程序中使用线程池能够提高线程的使用效率…...

【Spring】难理解的Aop编程 | 入门?
作者:狮子也疯狂 专栏:《spring开发》 坚持做好每一步,幸运之神自然会驾凌在你的身上 目录一. 🦁 前言二. 🦁 常见概念2.1 常见术语2.2 AOP入门Ⅰ. 🐇 功能场景Ⅱ. 🐇 实现过程2.3 通知类型Ⅰ.…...

2 月 25 日,论道京城 | 云原生开源项目应用实践报名开启
在数字化转型的浪潮中,云原生已经逐渐成为人们关注的焦点。开源社区作为云原生技术创新的根据地,为云原生的产业发展打造了丰富的技术生态圈,也在广泛的实践中源源不断地创造着新的机遇。想知道云原生存储技术实现了怎样的突破吗?…...

第五、六章 贪心算法、回溯算法
贪心算法 适合于贪心算法求解的问题具有:贪心选择性质、最优子结构性质。 贪心算法可以获取到问题的局部最优解,不一定能获取到全局最优解。 贪心算法总是作出在当前看来最好的选择;并且每次贪心选择都能将问题化简为一个更小的与原问题具有…...
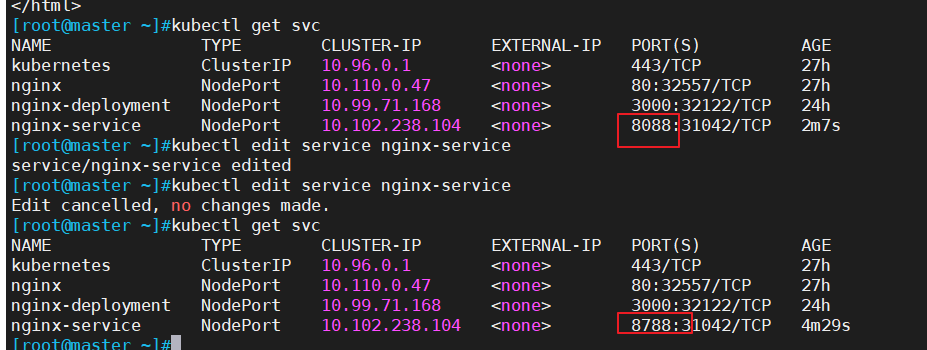
k8s-kubectl命令
文章目录一、kubectl 基本命令1、陈述式资源管理方法:2、声明式资源管理办法二、基本信息查看三、项目的生命周期创建kubectl run命令四、金丝雀发布(Canary Release)——陈述式管理方法五、声明式管理方法kubectl create 和 kubectl apply区别一、kubectl 基本命令 1、陈述式…...
36、基于51单片机频率计 LCD 1602显示系统设计
摘要 数字频率计是一种基本的测量仪器。它被广泛应用于航天、电子、测控等领域,还被应用在计算机及各种数学仪表中。一般采用的是十进制数字,显示被测信号频率。基本功能是测量正弦信号,方波信号以及其他各种单位时间内变坏的物理量。由于其…...
【vue】elemente-ui table toggleRowSelection 默认选择无效[已解决]
项目场景: 点击按钮,弹出一个弹出框,内部出现一个table表,表内数据是动态获取,同时得勾选上几个table表的数据,类似以下的图 问题描述 点击按钮显示弹出框,加载table中的数据,默…...
 HttpMessageConverter扩展)
SpringMVC DispatcherServlet源码(5) HttpMessageConverter扩展
前文通过阅读源码,深入分析了DispatcherServlet及相关组件的工作流程,本文不再阅读源码,介绍一下扩展HttpMessageConverter的方式。 HttpMessageConverter工作方式及扩展方式 前文介绍过,HttpMessageConverter是读写请求体和响应…...

day16_API
今日内容 上课同步视频:CuteN饕餮的个人空间_哔哩哔哩_bilibili 同步笔记沐沐霸的博客_CSDN博客-Java2301 零、 复习昨日 一、作业 二、String 三、StringBuffer&StringBuilder 四、日期 零、 复习昨日 见晨考 一、String String代表字符串,类,java程序中的所有字符串&…...

十二月券商金工精选
✦研报目录✦ ✦简述✦ 按发布时间排序 华宝证券 主动暴露的得与失—从Barra框架到私募指增因子分析方法 发布日期:2022-12-01 关键词:股票、Barra、风险暴露、指数增强 主要内容:本文针对私募指数增强产品的策略流程,设计…...

JUnit
Junit 简介 JUnit是一个开源的java单元测试框架,它是XUnit测试体系架架构的一种体现 是Java语言事实上的标准单元测试库真正的优势来自于JUnit所采作用的思想和技术,而不是框架本身。推动了单元测试、测试先行的编程和测试驱动的开发JUnit衍生了许多xUn…...

MySQL学习笔记4-乐观锁和悲观锁
1.定义 乐观锁和倍灌水是并发控制采用的技术手段,确保当多个数位同时对数据中同一数据存取时,不会破坏事物的隔离性、统一性和数据库统一性 乐观锁 假定不会发生并发冲突,只在提交操作时检测是否违反数据完整性 实现方式: 记录…...

Linux应用开发之网络套接字编程(实例篇)
服务端与客户端单连接 服务端代码 #include <sys/socket.h> #include <sys/types.h> #include <netinet/in.h> #include <stdio.h> #include <stdlib.h> #include <string.h> #include <arpa/inet.h> #include <pthread.h> …...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

剑指offer20_链表中环的入口节点
链表中环的入口节点 给定一个链表,若其中包含环,则输出环的入口节点。 若其中不包含环,则输出null。 数据范围 节点 val 值取值范围 [ 1 , 1000 ] [1,1000] [1,1000]。 节点 val 值各不相同。 链表长度 [ 0 , 500 ] [0,500] [0,500]。 …...

VTK如何让部分单位不可见
最近遇到一个需求,需要让一个vtkDataSet中的部分单元不可见,查阅了一些资料大概有以下几种方式 1.通过颜色映射表来进行,是最正规的做法 vtkNew<vtkLookupTable> lut; //值为0不显示,主要是最后一个参数,透明度…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

Docker 本地安装 mysql 数据库
Docker: Accelerated Container Application Development 下载对应操作系统版本的 docker ;并安装。 基础操作不再赘述。 打开 macOS 终端,开始 docker 安装mysql之旅 第一步 docker search mysql 》〉docker search mysql NAME DE…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...
