数据结构与算法细节篇之最短路径问题:Dijkstra和Floyd算法详细描述,java语言实现。
文章目录
- 前言
- 一、单源最短路径
- 1、单源最短路径问题
- 2、Dijkstra 初始化
- a、参数
- b、初始化参数
- c、算法步骤
- 3、Dijkstra 算法详细步骤
- a、第一轮算法执行
- b、第二轮算法执行
- c、第三轮算法执行
- d、第四轮算法执行
- e、第五轮算法执行
- f、第六轮算法执行
- 4、java算法实现
- 二、多源最短路径
- 1、多源最短路径问题
- 2、Floyd初始化
- a、参数
- b、参数初始化
- c、算法步骤
- 3、Floyd算法详细步骤
- 4、java 算法实现
前言
- 最短路径的算法有两个,Dijkstra算法 和 Floyd算法。
- Dijkstra算法 解决的是 单源 最短路径问题。
- Floyd算法解决的是 多源 最短路径问题,并且可以处理负权图。
- 今天要讲的就是Dijkstra算法。
- 加:
feng--Insist(大写的i),进java交流群讨论互联网+技术。可索要PPT等资料。 - 其他资料,建议先看本篇博客。:Dijkstra算法和Floyd算法:https://blog.csdn.net/weixin_43872728/article/details/100662957
- 代码位置:https://github.com/fengfanli/dataStructuresAndAlgorithm/tree/master/src/com/feng/algorithm/self_learn
一、单源最短路径
1、单源最短路径问题
- 解决的问题: 求解单源最短路径,即各个节点到达源点的最短路径或权值。如下图中

考察其他所有节点到源点的最短路径和长度 - 局限性: 无法解决权值为负数的情况
- 资料
- 可先看匹配视频:https://www.bilibili.com/video/BV1o44y1B7NM/
- 代码:待上传。
2、Dijkstra 初始化
首先已知的是:
给定 邻接矩阵表示的图Graph、源点S、终点T。
a、参数
参数:
| 参数名 | 解释 |
|---|---|
| S | 记录当前已经处理过的源点到最短节点 |
| U | 记录还未处理的节点 |
| dist[] | 记录各个节点到起始节点的最短权值 |
| path[] | 记录各个节点的上一级节点(用来联系该节点到起始节点的路径) |
b、初始化参数
- 顶点集S: 节点A到自已的最短路径长度为0。只包含源点,即S={A},代码中没有这个,这里是为了步骤清晰而设置的。
- 顶点集U: 包含除A外的其他顶点. 即U={B,C,D,E,F,G}
- dist[]: 源点还不能到达的节点,其权值为∞
| 名 | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| dist[]: | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 初始化值: | 0 | 4 | 6 | 6 | ∞ | ∞ | ∞ |
path[]: 记录当前节点的前驱节点下标(源点还不能到达的节点为-1)
| 名 | A | B | C | D | E | F | G |
|---|---|---|---|---|---|---|---|
| path[]: | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| 初始化值: | 0 | 0 | 0 | 0 | -1 | -1 | -1 |
c、算法步骤
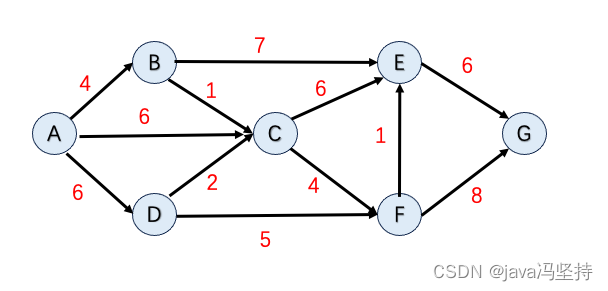
- 初始化:设定除源节点以外的其它所有节点到源节点的距离为INFINITE(一个很大的数),且这些节点都没被处理过。如上图所示
- 从源节点出发,更新相邻节点(图中为B、C、D)到源节点的距离。然后在所有节点中选择一个最段距离的点作为当前节点。
- 标记当前节点为done(表示已经被处理过),与步骤2类似,更新其相邻节点的距离。(这些相邻节点的距离更新也叫
松弛,目的是让它们与源节点的距离最小。因为你是在当前最小距离的基础上进行更新的,由于当前节点到源节点的距离已经是最小的了,那么如果这些节点之前得到的距离比这个距离大的话,我们就更新它)。 - 步骤3做完以后,设置这个当前节点已被done,然后寻找下一个具有最小代价(cost)的点,作为新的当前节点,重复步骤3.
- 如果最后检测到目标节点时,其周围所有的节点都已被处理,那么目标节点与源节点的距离就是最小距离了。如果想看这个最小距离所经过的路径,可以回溯,前提是你在步骤3里面加入了当前节点的最优路径前驱节点信息。
- 我总结了下可用如下几句话代替:
两步走- 从dist[]中在集合U中的选择最小距离加入到S中,作为当前节点。(最小距离:就是 当前节点到源点的最小距离)
- 遍历当前节点的邻边节点:更新dist[]和path[]
- 如果经过当前节点+邻边权重 < 邻边节点,则改变dist[]和path[],否者不改变。
3、Dijkstra 算法详细步骤
a、第一轮算法执行
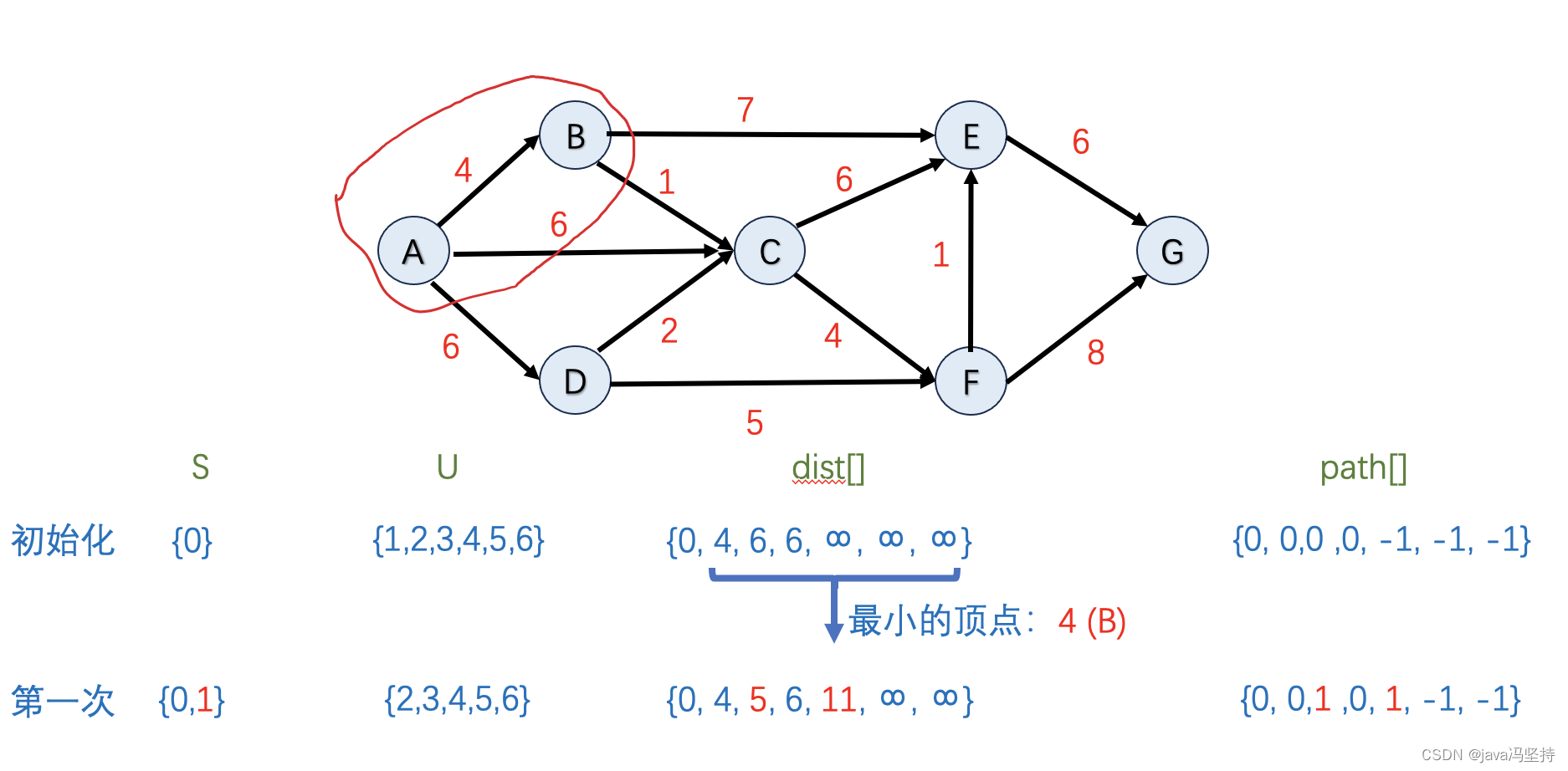
-
如上图,因为dist[]中排出掉集合U中节点,最小值是4,也就是节点B,所以将B纳入到集合S中(圈中)。
-
首先 在dist[]数组中并在集合U中 最小值是节点B,既当前节点,其邻边有C和E,所以看是否要更新C和E。
- 节点C:因为
C的最小距离dist[1](B的最小距离)4+1(B到C的距离)=5 < dist[2](C的最小距离) = 6,所以 dist[2]=5,path[2]=1 - 节点E:因为
E的最小距离 dist[1](B的最小距离)4+7(B到E的距离)=11 < dist[4] (E的最小距离)=无穷大,所以 dist[4]=11,path[4]=1
- 节点C:因为
-
第一轮算法两个邻边节点C、E有改变
b、第二轮算法执行
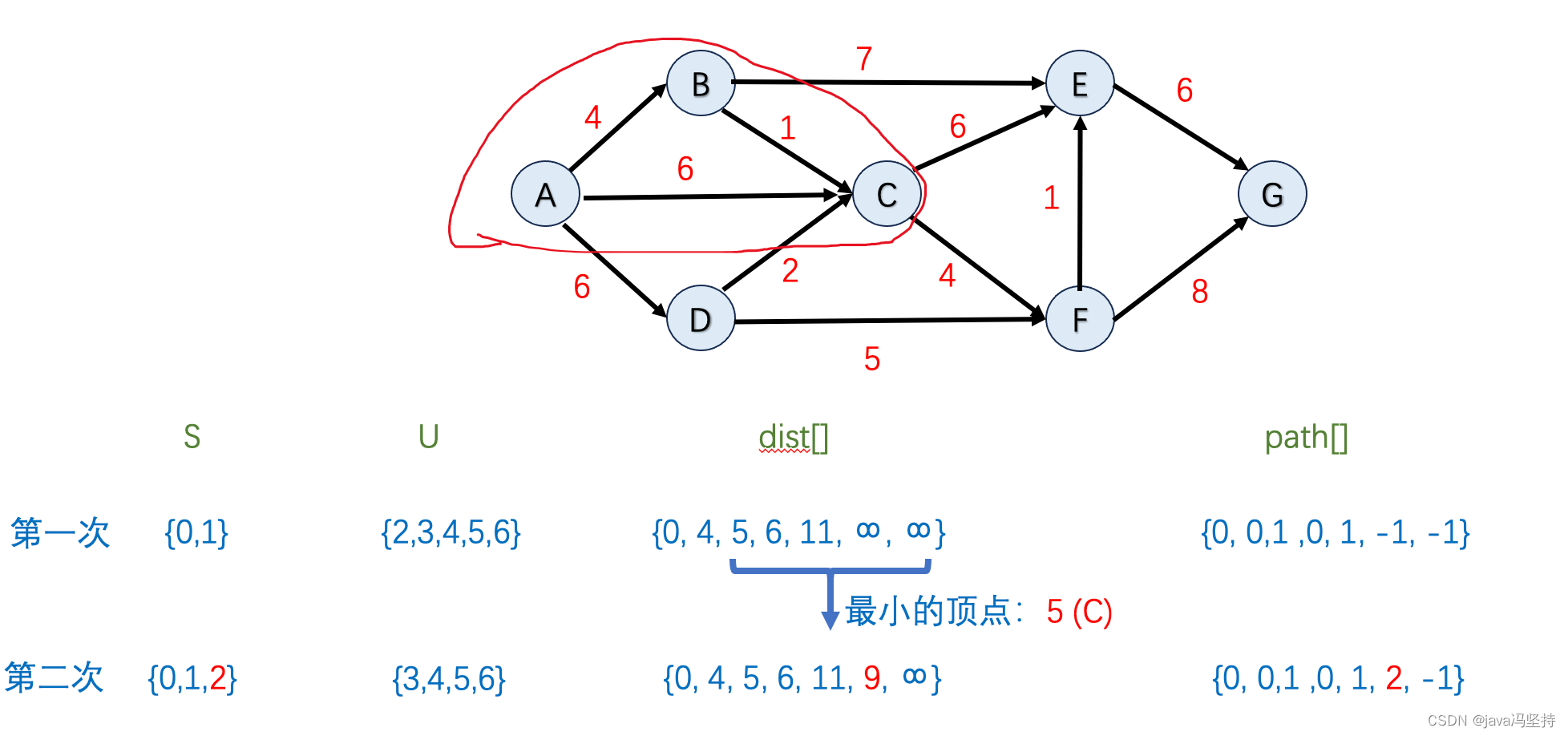
- 如上图,因为dist[]中排出掉集合U中节点,最小值是5,也就是节点C,所以将C纳入到集合S中(圈中)。
- 首先在dist[]数组中并在集合U中 最小值是节点C,既当前节点,其邻边有E和F,所以看是否要更新E和F。
- 节点E:因为
C的最小距离 dist[2](也就是C的最小距离)5+6(C到E的距离)=11 == dist[4](E的最小距离) = 11,所以不动 - 节点F:因为
F的最小距离 dist[2](也就是C的最小距离)5+4(C到F的距离)=9 < dist[5] (F的最小距离)=无穷大,所以 dist[5]=9,path[5]=2
- 节点E:因为
- 第二轮算法两个邻边节点仅有 F有改变
c、第三轮算法执行
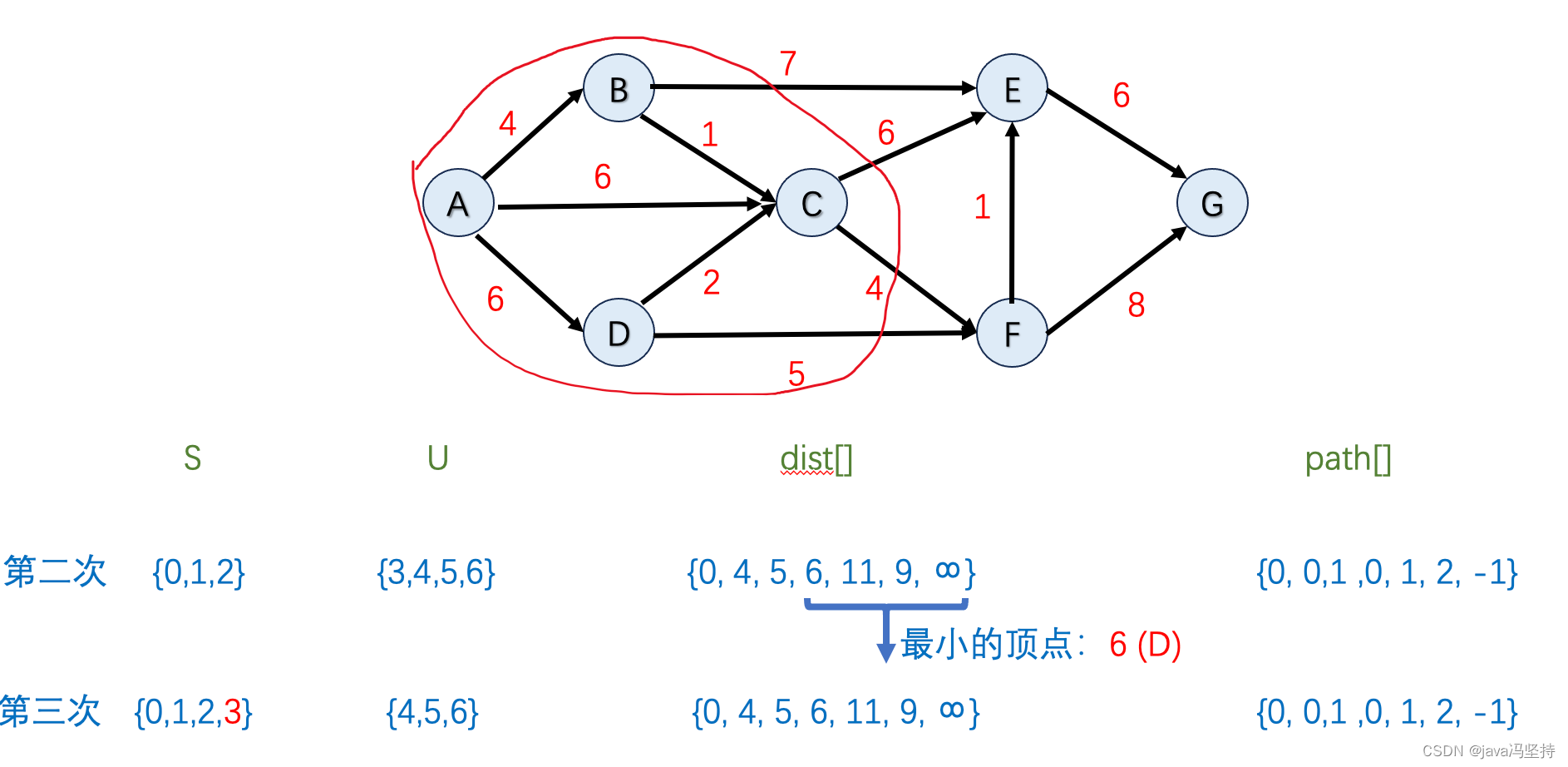
- 如上图,因为dist[]中排出掉集合U中节点,最小值是6,也就是节点D,所以将D纳入到集合S中(圈中)。
- 首先在dist[]数组中并在集合U中 最小值是节点D,既当前节点,其邻边有C和F,所以看是否要更新C和F。
- 节点C:因为
C的最小距离 dist[3](也就是D的最小距离)6+2(D到C的距离)=8 > dist[2](C的最小距离) = 5,所以不动 - 节点F:因为
F的最小距离 dist[3](也就是D的最小距离)6+5(D到F的距离)=11 > dist[5] (F的最小距离)=9,所以不动 - 第三轮算法两个邻边节点C、F都没有改变
d、第四轮算法执行
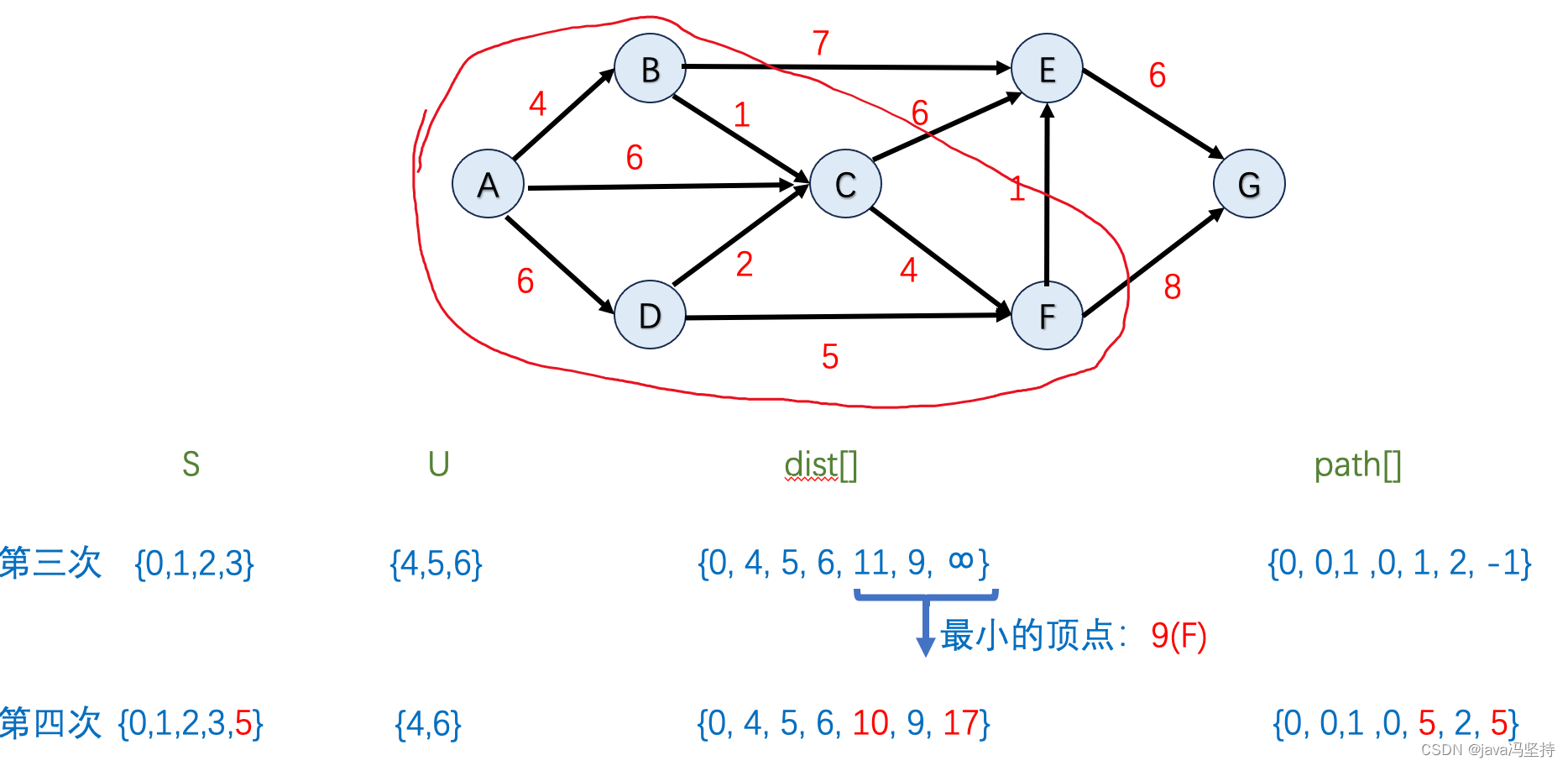
- 如上图,因为dist[]中排出掉集合U中节点,最小值是9,也就是节点F,所以将F纳入到集合S中(圈中)。
- 首先在dist[]数组中并在集合U中 最小值是节点F,既当前节点,其邻边有E和G,所以看是否要更新E和G 。
- 节点E:因为
E的最小距离 dist[5](也就是F的最小距离) 9 +1(F到E的距离)=10 < dist[4](E的最小距离) =11,所以 dist[4] = 10,path[4]=5 - 节点G:因为
G的最小距离 dist[5](也就是F的最小距离) 9 +8(F到G的距离)=17 < dist[6](G的最小距离) =无穷大,所以 dist[6]=17,path[6]=5 - 第四轮算法两个邻边节点E、G都有改变
e、第五轮算法执行
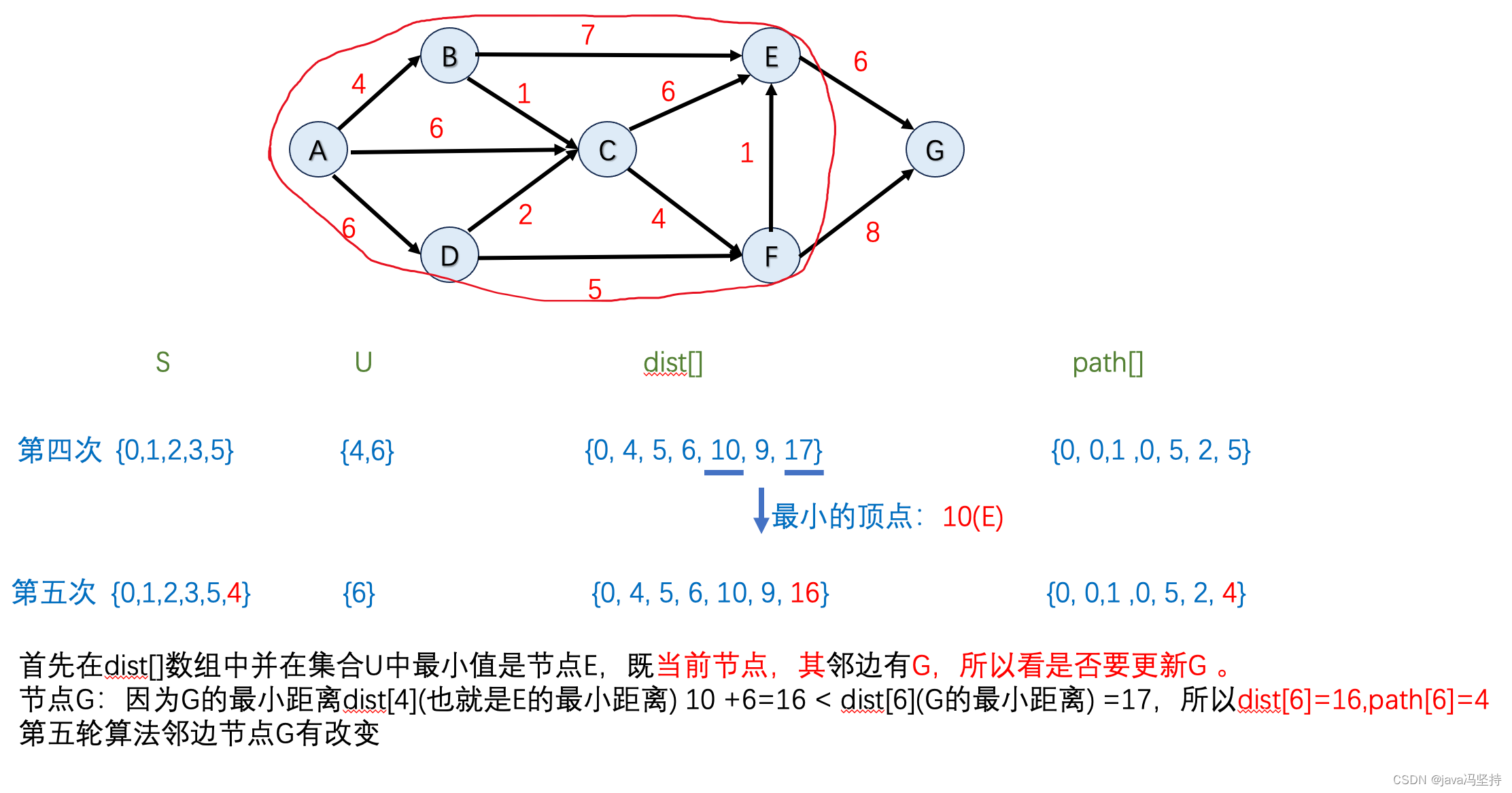
- 如上图,因为dist[]中排出掉集合U中节点,最小值是9,也就是节点F,所以将F纳入到集合S中(圈中)。
- 首先在dist[]数组中并在集合U中 最小值是节点E,既当前节点,其邻边有G,所以看是否要更新G 。
- 节点G:因为
G的最小距离 dist[4](也就是E的最小距离) 10 +6(E到G的距离)=16 < dist[6](G的最小距离) =17,所以 dist[6]=16,path[6]=4 - 第五轮算法邻边 节点G有改变
f、第六轮算法执行
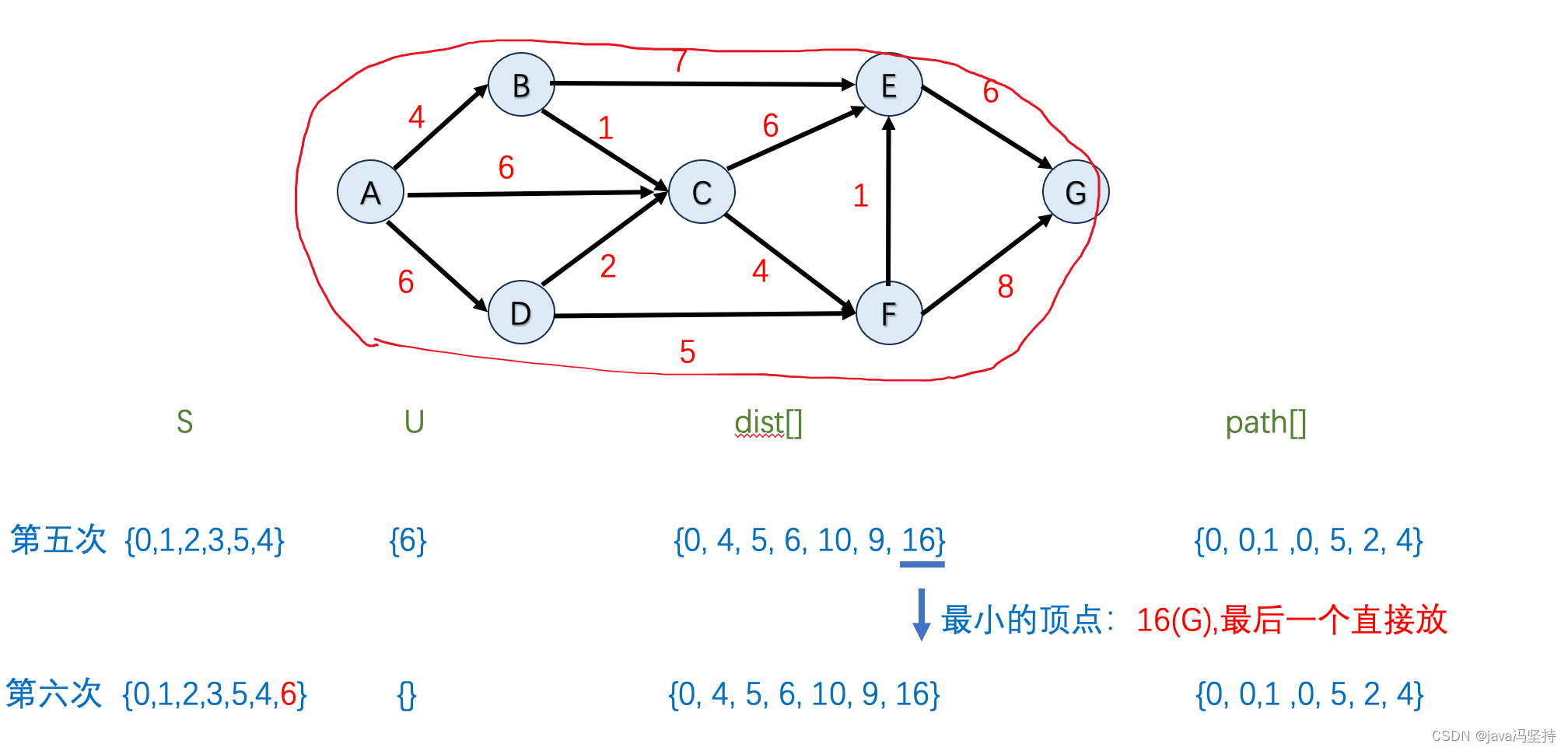
- 如上图,因为dist[]中排出掉集合U中节点,最小值是16,也就是节点G,所以将G纳入到集合S中(圈中)。
- 首先在dist[]数组中并在集合U中 最小值是节点G,既当前节点,其没有邻边。
- 第六轮算法邻边节点G没有改变
- 到此算法遍历结束
4、java算法实现
给定矩阵表示的Graph结构。输入源点v0和终点v1。
二、多源最短路径
1、多源最短路径问题
- 上面的Dijkstra 解决的是单源最短路径的问题,首先要给定 开始节点和终止结点,如果换了开始和终止节点,那就要每次都要重新跑一次。
- 那就引出了多源最短路径问题:就是执行一次算法,求出每两个点之间的最短距离,这就是多源最短路径算法。这个算法代码略简单一些。
- 思想只有一个:要算两个点之间的最短距离,就看有没有第三个点使得
2、Floyd初始化
首先已知的是:
给定 **邻接矩阵表示的图Graph。
a、参数
| 参数名 | 解释 |
|---|---|
| A[][] | 函数中的参数,需要返回,存储的是节点的前置节点。 |
| path[][] | 存储的是每两点之间的所需距离。 |
b、参数初始化
| 参数名 | 解释 |
|---|---|
| A[][] | 就是图的赋值,从代码中可以看出,比较简单 |
| path[][] | 默认都是-1.表示从A点到B点是直达的。 |
c、算法步骤
- 对于每个顶点
v(体现在代码的第一层for循环),和任意一顶点(i,j)(体现代码的第二、三层循环),切i!=j、v!=i、v!=j。 - 如果
A[i][j] > A[i][v] + A[]v[j],则将A[i][j] 更新为 A[i][v] + A[v][j]的值,并且将path[i][j]改为v。
3、Floyd算法详细步骤
4、java 算法实现
package com.feng.algorithm.self_learn.floyd.floyd1;/*** 学习视频:https://www.bilibili.com/video/BV1LE411R7CS*/
public class FloydAlgorithm {public static void main(String[] args) {int[][] graph = new int[4][4];int N = Short.MAX_VALUE;graph[0] = new int[]{0, 5, N, 7};graph[1] = new int[]{N, 0, 4, 2};graph[2] = new int[]{3, 3, 0, 2};graph[3] = new int[]{N, N, 1, 0};int[][] path = new int[4][4];int[][] A = Floyd.floyd(graph, path);int u = 1;int v = 0;Floyd.printPath(u, v, path);System.out.println();System.out.println(u + "->" + v +" shortest path is :" + A[u][v]);}
}
class Floyd {/*** 佛洛依德算法,给定邻接矩阵表示的图,* path[][]:存放路径中间的节点,如果是-1就是直达* A[][]:存放任意两个节点之间的距离* 举例:从1-0,从A得出距离是6,从path得出 1-3-2-0* @param graph* @param path*/static int[][] floyd(int[][] graph, int[][] path) {int n = graph.length;int v, i, j;int[][] A = new int[n][n];for (i = 0; i < n; i++) {for (j = 0; j < n; j++) {A[i][j] = graph[i][j];path[i][j] = -1;}}for (v = 0; v < n; v++) {for (i = 0; i < n; i++) {for (j = 0; j < n; j++) {if (A[i][j] > A[i][v] + A[v][j]) {A[i][j] = A[i][v] + A[v][j];path[i][j] = v;}}}}return A;}/*** 递归打印路径* @param u* @param v* @param path*/static void printPath(int u, int v, int[][] path) {if (path[u][v] == -1) { // 如果等于 -1 。说明就是直达的System.out.printf(u + "->" + v + " ");} else {int mid = path[u][v];printPath(u, mid, path);printPath(mid, v, path);}}
}相关文章:

数据结构与算法细节篇之最短路径问题:Dijkstra和Floyd算法详细描述,java语言实现。
文章目录 前言一、单源最短路径1、单源最短路径问题2、Dijkstra 初始化a、参数b、初始化参数c、算法步骤 3、Dijkstra 算法详细步骤a、第一轮算法执行b、第二轮算法执行c、第三轮算法执行d、第四轮算法执行e、第五轮算法执行f、第六轮算法执行 4、java算法实现 二、多源最短路径…...
改进YOLO系列:6.添加ECA注意力机制
添加ECA注意力机制 1. ECA注意力机制论文2. ECA注意力机制原理3. ECA注意力机制的配置3.1common.py配置3.2yolo.py配置3.3yaml文件配置1. ECA注意力机制论文 论文题目:ECA-Net: Efficient Channel Attention for Deep Convolutional Neural Networks 论文链接:ECA-N…...
软件测试知识点总结(一)
文章目录 前言一. 什么是软件测试二. 软件测试和软件调试的区别三. 软件测试和研发的区别四. 优秀的测试人员所应该具备的素质总结 前言 在现实生活中的很多场景下,我们都会进行测试。 比如买件衣服,我们需要看衣服是不是穿着好看,衣服材质如…...

持续集成与持续交付:现代软件测试的变革之路
引言 在数字化时代,软件开发的速度和复杂性都在不断增加。为了满足市场的需求,企业需要更快、更高效地交付高质量的软件产品。在这样的背景下,持续集成与持续交付(CI/CD)成为了软件开发和测试的核心实践。 软件开发的…...
深度学习基本理论下篇:(梯度下降/卷积/池化/归一化/AlexNet/归一化/Dropout/卷积核)、深度学习面试
深度学习基本理论上篇:(MLP/激活函数/softmax/损失函数/梯度/梯度下降/学习率/反向传播) 深度学习基本理论上篇:(MLP/激活函数/softmax/损失函数/梯度/梯度下降/学习率/反向传播)、深度学习面试_会害羞的杨…...
)
[Ubuntu 20.04] 通过udev规则修改网卡名称(例如eth0)
在 Ubuntu 20.04 操作系统中,默认情况下,网卡接口名称采用了一种较为复杂的命名方式(如 enp0s3、eth0 等)。然而,有时候我们可能更希望使用更简洁和易于识别的名称来标识不同的网络接口。那么如何在 Ubuntu 20.04 中修改网卡接口的名称,以满足个性化需求。 步骤一:查看当…...

Java“牵手”根据关键词搜索(分类搜索)lazada商品列表页面数据获取方法,lazadaAPI实现批量商品数据抓取示例
lazada商城是一个网上购物平台,售卖各类商品,包括服装、鞋类、家居用品、美妆产品、电子产品等。要获取lazada商品列表和商品详情页面数据,您可以通过开放平台的接口或者直接访问lazada商城的网页来获取商品详情信息。以下是两种常用方法的介…...
Java—实现多线程程序 | 入门
目录 一、前言 二、基本概念 进程 线程 三、Java多线程实现 java.lang.Thread类 获取线程名字及对象 获取main进程名 Thread currentThread() 四、线程优先级 设置优先级 一、前言 前期入门学习的代码中,全部都是单线的程序,也就是从头到尾…...

8.5 【C语言】指向函数的指针
8.5.1 什么是函数的指针 每次调用函数时都从该地址入口开始执行此段函数代码。函数名代表函数的起始地址。 8.5.2 用函数指针变量调用函数 例8.22 用函数求整数a和b中的大者 解题思路:在主函数调用max函数,除了可以通过函数名调用外,还可…...

C++实现字符串的逆置
目录 C和C的区别 【1】C对C的扩充 【2】C对C的兼容 第一个C程序 【1】hello world 【2】cout标准输出流对象 i)介绍 ii)运算 iii)cout的使用 iv)使用cout指定格式的输出 练习:1、输出斐波那契的前10项。 【3】…...

论Spring或Spring Boot的花式扩展
文章目录 引言扩展点讲述花式扩展之自动配置类花式扩展之实现接口实现方式样例 花式扩展之自定义starterImport方式SpringFactories方式 总结鸣谢 引言 Spring Boot是一个高度可定制的框架,旨在帮助开发者快速创建、配置和管理他们的应用程序 扩展点讲述 Spring Bo…...

如何评估分类模型的好坏
如何评估分类模型的好坏 评估分类预测模型的质量,常用一个矩阵、三条曲线和六个指标。 一个矩阵:混淆矩阵;三条曲线:ROC曲线、PR曲线、KS曲线;六个指标:正确率Acc、查全率R、查准率P、F值、AUC、BEP值、KS…...

● 84.柱状图中最大的矩形
84.柱状图中最大的矩形 class Solution { public:int largestRectangleArea(vector<int>& heights) {stack<int>st;heights.insert(heights.begin(),0);heights.push_back(0);st.push(0);int res0;for(int i1;i<heights.size();i){while(heights[i]<heig…...

未检查的转换: ‘java.lang.Object‘ 转换为 ‘java.util.List
fastjson方式 Object object ... // 获取待转换的objectList<WbsCategory> list JSON.parseObject(JSON.toJSONString(object), new TypeReference<List<WbsCategory>>() {}); 在这个示例中,我们使用JSON.toJSONString()将object对象转换…...
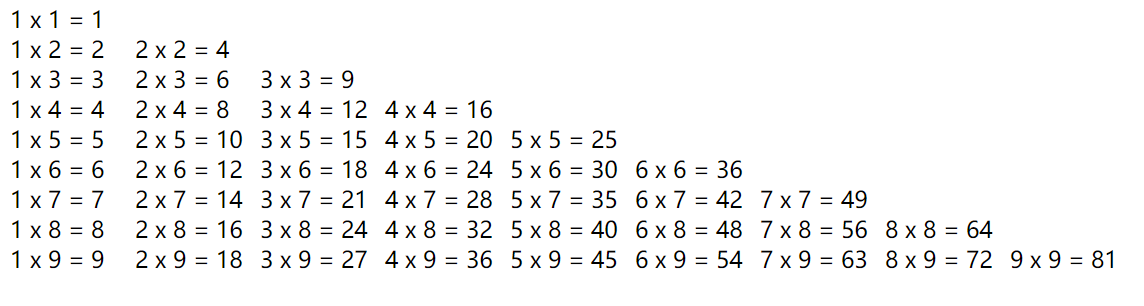
【C语言】使用C语言,实现九九乘法表(另附Python、Java、JavaScript实现方式)
文章目录 1. C语言实现1.1 思路1.2 代码实现 3.其他语言实现3.1 Python实现3.2 Java实现3.3 JavaScript实现 1. C语言实现 1.1 思路 九九乘法表图示: 思路如下:定义两层for循环即可实现九九乘法表 一共有9层,所以要定义一个变量iÿ…...

[机缘参悟-102] :IT人 - 管理的本质?管理人与从事技术的本质区别?人性、冰山模型、需求层次模型
感悟: 管理的本质是:学习各种管理理论、方法、技能,克服自身的人性缺点、预防他人人性的恶点、利用他人的人性特点拿到结果,从而完成组织、管理者的上司、管理者自身、管理者下属的目标。管理中的问题,80%以上都人性问…...
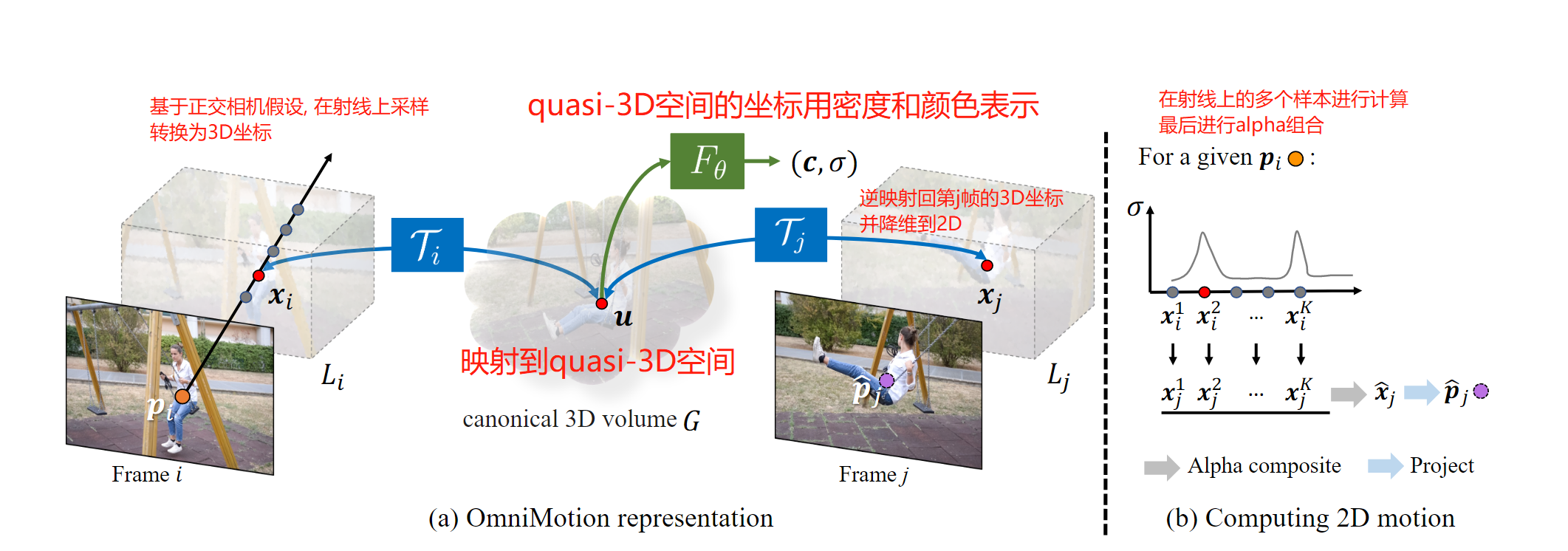
[论文阅读笔记26]Tracking Everything Everywhere All at Once
论文地址: 论文 代码地址: 代码 这是一篇效果极好的像素级跟踪的文章, 发表在ICCV2023, 可以非常好的应对遮挡等情形, 其根本的方法在于将2D点投影到一个伪3D(quasi-3D)空间, 然后再映射回去, 就可以在其他帧中得到稳定跟踪. 这篇文章的方法不是很好理解, 代码也刚开源, 做一…...
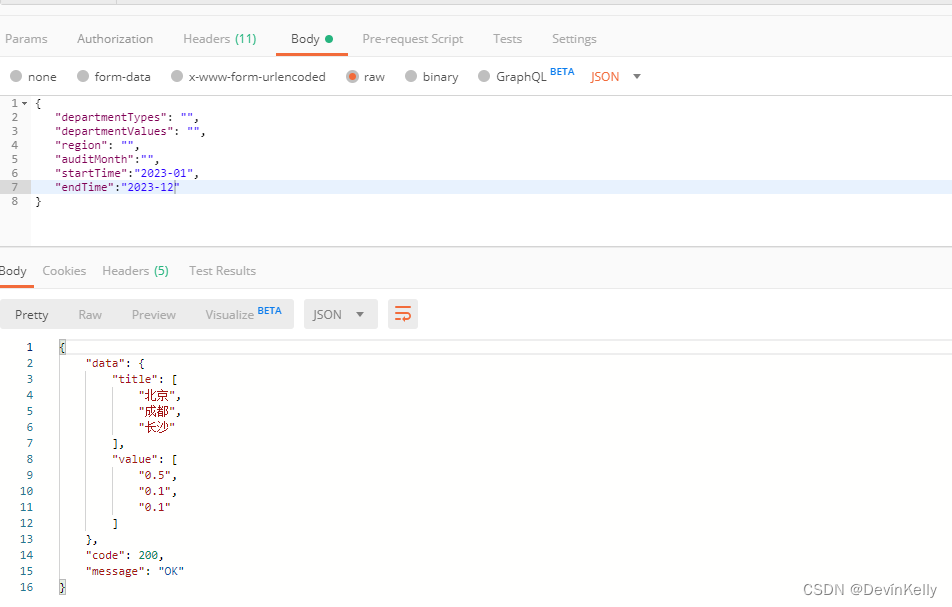
【Java 动态数据统计图】前后端对接数据格式(Map返回数组格式数据)六(120)
说明: 前端使用:vue3.0 前后端对接数据格式:无非就是前端把后端返回的数据处理为自己想要的格式,或者,后端给前端处理好想要的格式; 针对前后端的柱状图,趋势图等数据对接,前端一般需…...
❤ 给自己的mac系统上安装java环境
❤ 给自己的mac系统上安装java环境 🍓 作为前端工程师如何给自己的mac系统上安装java环境 🍎 最近因为自己的一些项目需求,mac电脑上需要安装一些后台的java环境,用来跑后台的java程序,于是从一个前端工程师的角度安…...

Java-匿名类
介绍 匿名类是指没有名字的类,它对一个给定的类进行拓展,或者实现一个给定的接口。使用匿名类可以使得代码更加简洁、紧凑、模块程度更高。 实现方式及语法 匿名类有两种实现方式 继承一个类,重写其方法实现一个接口(可以是多…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

逻辑回归:给不确定性划界的分类大师
想象你是一名医生。面对患者的检查报告(肿瘤大小、血液指标),你需要做出一个**决定性判断**:恶性还是良性?这种“非黑即白”的抉择,正是**逻辑回归(Logistic Regression)** 的战场&a…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

Python爬虫实战:研究feedparser库相关技术
1. 引言 1.1 研究背景与意义 在当今信息爆炸的时代,互联网上存在着海量的信息资源。RSS(Really Simple Syndication)作为一种标准化的信息聚合技术,被广泛用于网站内容的发布和订阅。通过 RSS,用户可以方便地获取网站更新的内容,而无需频繁访问各个网站。 然而,互联网…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

解读《网络安全法》最新修订,把握网络安全新趋势
《网络安全法》自2017年施行以来,在维护网络空间安全方面发挥了重要作用。但随着网络环境的日益复杂,网络攻击、数据泄露等事件频发,现行法律已难以完全适应新的风险挑战。 2025年3月28日,国家网信办会同相关部门起草了《网络安全…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...
