【GeoDa实用技巧100例】022：geoda生成空间权重矩阵（邻接矩阵、距离矩阵）
geoda生成空间权重矩阵（邻接矩阵、距离矩阵），车式矩阵、后式矩阵、K邻接矩阵。
文章目录
- 一、概述
- 二、“车式”邻接的gal文档生成
- 三、“后式”邻接gal文档生成
- 四、k最近邻居gat文档生成
- 五、查看gal和gat文档
一、概述
空间权重矩阵(或相应的表格形式)一般需要用计算机软件生成。在GeoDa中，无法直接生成空间权重矩阵，只能生成它的表格形式，即邻接关系的gal文档和距离关系的gat文档，两者都可以用Notepad++打开（推荐使用）。下面我们用萨克拉门托(sacramentot)人口调查资料为例，说明用GeoDa生成“车式”邻接、“后式”邻接和k最近邻居空间权重矩阵的gal(或gwt)文档。
二、“车式”邻接的gal文档生成
在GeoDa中，建立空间权重gal文档的基本步骤如下：
打开底图(文档sacramentot2.shp，关键词POLYID)：
点击【工具】→【空间权重管理】，打开空间权重管理对话框。
相关文章：
【GeoDa实用技巧100例】022：geoda生成空间权重矩阵（邻接矩阵、距离矩阵）
geoda生成空间权重矩阵（邻接矩阵、距离矩阵），车式矩阵、后式矩阵、K邻接矩阵。 文章目录 一、概述二、“车式”邻接的gal文档生成三、“后式”邻接gal文档生成四、k最近邻居gat文档生成五、查看gal和gat文档一、概述 空间权重矩阵(或相应的表格形式)一般需要用计算机软件生…...
基于web的鲜花商城系统java jsp网上购物超市mysql源代码
本项目为前几天收费帮学妹做的一个项目，Java EE JSP项目，在工作环境中基本使用不到，但是很多学校把这个当作编程入门的项目来做，故分享出本项目供初学者参考。 一、项目描述 基于web的鲜花商城系统 系统有2权限：前台…...
意外发现Cortex-M内核带的64bit时间戳，比32bit的DWT时钟周期计数器更方便，再也不用担心溢出问题了
视频： https://www.bilibili.com/video/BV1Bw411D7F5 意外发现Cortex-M内核带的64bit时间戳，比32bit的DWT时钟周期计数器更方便，再也不用担心溢出问题了 介绍： 看参数手册的Debug章节，System ROM Table里面带Timestam…...
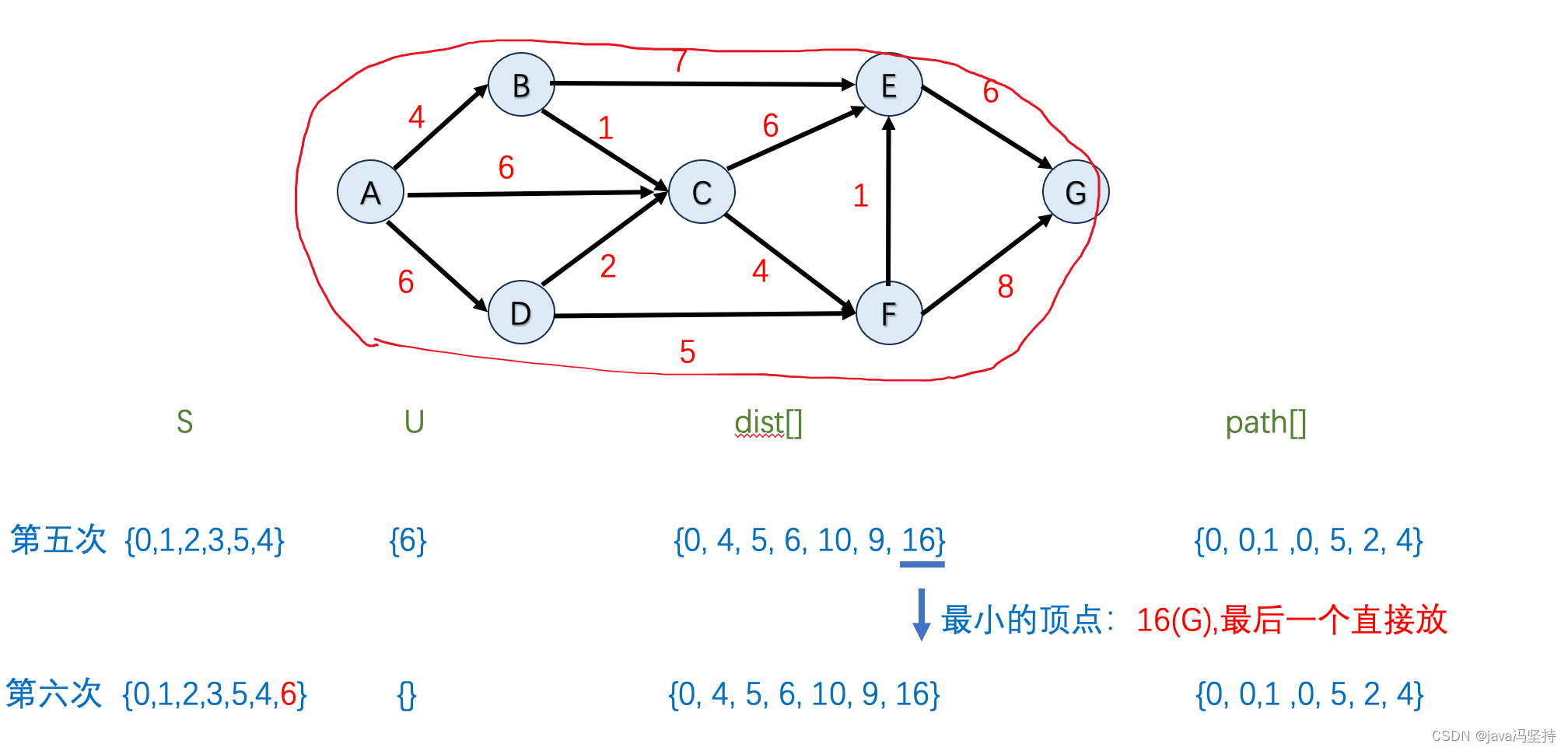
数据结构与算法细节篇之最短路径问题：Dijkstra和Floyd算法详细描述，java语言实现。
文章目录 前言一、单源最短路径1、单源最短路径问题2、Dijkstra 初始化a、参数b、初始化参数c、算法步骤 3、Dijkstra 算法详细步骤a、第一轮算法执行b、第二轮算法执行c、第三轮算法执行d、第四轮算法执行e、第五轮算法执行f、第六轮算法执行 4、java算法实现 二、多源最短路径…...
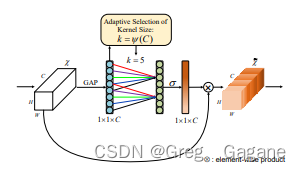
改进YOLO系列：6.添加ECA注意力机制
添加ECA注意力机制 1. ECA注意力机制论文２. ECA注意力机制原理３. ECA注意力机制的配置３.１common.py配置３.２yolo.py配置３.３yaml文件配置1. ECA注意力机制论文 论文题目：ECA-Net: Efficient Channel Attention for Deep Convolutional Neural Networks 论文链接：ECA-N…...
软件测试知识点总结（一）
文章目录 前言一. 什么是软件测试二. 软件测试和软件调试的区别三. 软件测试和研发的区别四. 优秀的测试人员所应该具备的素质总结 前言 在现实生活中的很多场景下，我们都会进行测试。 比如买件衣服，我们需要看衣服是不是穿着好看，衣服材质如…...
持续集成与持续交付：现代软件测试的变革之路
引言 在数字化时代，软件开发的速度和复杂性都在不断增加。为了满足市场的需求，企业需要更快、更高效地交付高质量的软件产品。在这样的背景下，持续集成与持续交付（CI/CD）成为了软件开发和测试的核心实践。 软件开发的…...
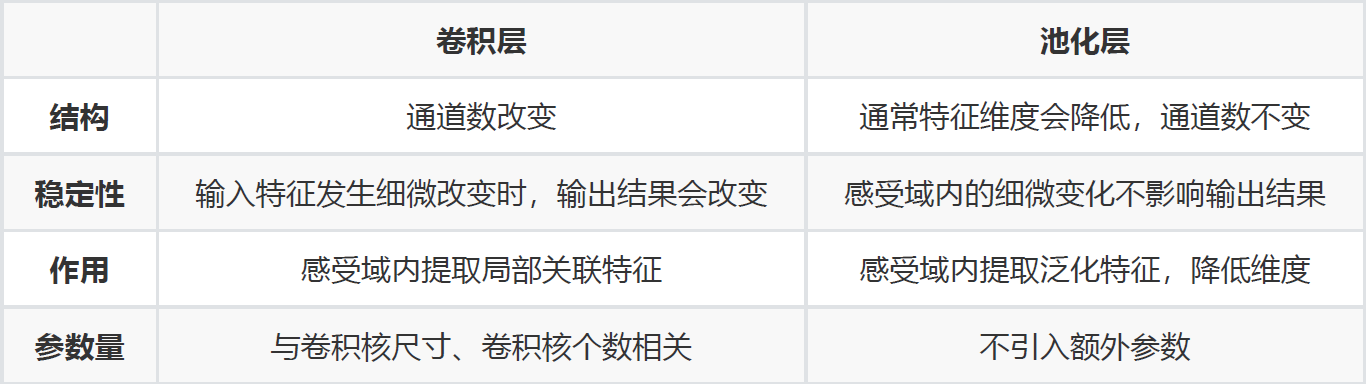
深度学习基本理论下篇：（梯度下降/卷积/池化/归一化/AlexNet/归一化/Dropout/卷积核）、深度学习面试
深度学习基本理论上篇：（MLP/激活函数/softmax/损失函数/梯度/梯度下降/学习率/反向传播） 深度学习基本理论上篇：（MLP/激活函数/softmax/损失函数/梯度/梯度下降/学习率/反向传播）、深度学习面试_会害羞的杨…...
[Ubuntu 20.04] 通过udev规则修改网卡名称（例如eth0）
在 Ubuntu 20.04 操作系统中，默认情况下，网卡接口名称采用了一种较为复杂的命名方式（如 enp0s3、eth0 等）。然而，有时候我们可能更希望使用更简洁和易于识别的名称来标识不同的网络接口。那么如何在 Ubuntu 20.04 中修改网卡接口的名称，以满足个性化需求。 步骤一：查看当…...
Java“牵手”根据关键词搜索（分类搜索）lazada商品列表页面数据获取方法，lazadaAPI实现批量商品数据抓取示例
lazada商城是一个网上购物平台，售卖各类商品，包括服装、鞋类、家居用品、美妆产品、电子产品等。要获取lazada商品列表和商品详情页面数据，您可以通过开放平台的接口或者直接访问lazada商城的网页来获取商品详情信息。以下是两种常用方法的介…...
Java—实现多线程程序 | 入门
目录 一、前言 二、基本概念 进程 线程 三、Java多线程实现 java.lang.Thread类 获取线程名字及对象 获取main进程名 Thread currentThread() 四、线程优先级 设置优先级 一、前言 前期入门学习的代码中，全部都是单线的程序，也就是从头到尾…...
8.5 【C语言】指向函数的指针
8.5.1 什么是函数的指针 每次调用函数时都从该地址入口开始执行此段函数代码。函数名代表函数的起始地址。 8.5.2 用函数指针变量调用函数 例8.22 用函数求整数a和b中的大者 解题思路：在主函数调用max函数，除了可以通过函数名调用外，还可…...
C++实现字符串的逆置
目录 C和C的区别 【1】C对C的扩充 【2】C对C的兼容 第一个C程序 【1】hello world 【2】cout标准输出流对象 i）介绍 ii）运算 iii）cout的使用 iv）使用cout指定格式的输出 练习：1、输出斐波那契的前10项。 【3】…...
论Spring或Spring Boot的花式扩展
文章目录 引言扩展点讲述花式扩展之自动配置类花式扩展之实现接口实现方式样例 花式扩展之自定义starterImport方式SpringFactories方式 总结鸣谢 引言 Spring Boot是一个高度可定制的框架，旨在帮助开发者快速创建、配置和管理他们的应用程序 扩展点讲述 Spring Bo…...
如何评估分类模型的好坏
如何评估分类模型的好坏 评估分类预测模型的质量，常用一个矩阵、三条曲线和六个指标。 一个矩阵：混淆矩阵；三条曲线：ROC曲线、PR曲线、KS曲线；六个指标：正确率Acc、查全率R、查准率P、F值、AUC、BEP值、KS…...
● 84.柱状图中最大的矩形
84.柱状图中最大的矩形 class Solution { public:int largestRectangleArea(vector<int>& heights) {stack<int>st;heights.insert(heights.begin(),0);heights.push_back(0);st.push(0);int res0;for(int i1;i<heights.size();i){while(heights[i]<heig…...
未检查的转换: ‘java.lang.Object‘ 转换为 ‘java.util.List
fastjson方式 Object object ... // 获取待转换的objectList<WbsCategory> list JSON.parseObject(JSON.toJSONString(object), new TypeReference<List<WbsCategory>>() {}); 在这个示例中，我们使用JSON.toJSONString()将object对象转换…...
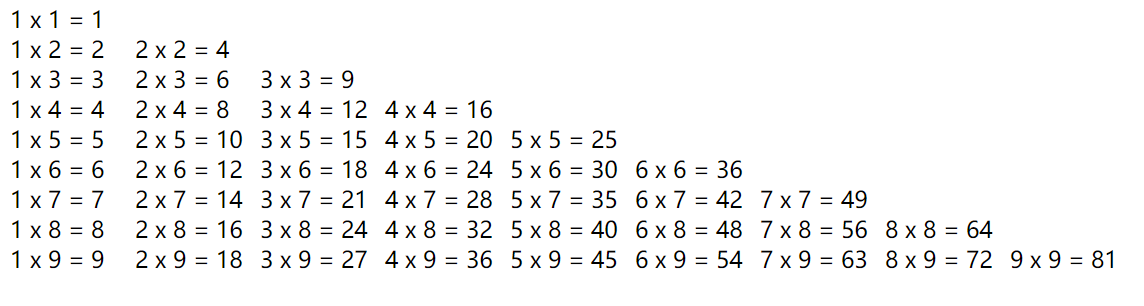
【C语言】使用C语言，实现九九乘法表（另附Python、Java、JavaScript实现方式）
文章目录 1. C语言实现1.1 思路1.2 代码实现 3.其他语言实现3.1 Python实现3.2 Java实现3.3 JavaScript实现 1. C语言实现 1.1 思路 九九乘法表图示： 思路如下：定义两层for循环即可实现九九乘法表 一共有9层，所以要定义一个变量iÿ…...
[机缘参悟-102] ：IT人 - 管理的本质？管理人与从事技术的本质区别？人性、冰山模型、需求层次模型
感悟： 管理的本质是：学习各种管理理论、方法、技能，克服自身的人性缺点、预防他人人性的恶点、利用他人的人性特点拿到结果，从而完成组织、管理者的上司、管理者自身、管理者下属的目标。管理中的问题，80%以上都人性问…...
[论文阅读笔记26]Tracking Everything Everywhere All at Once
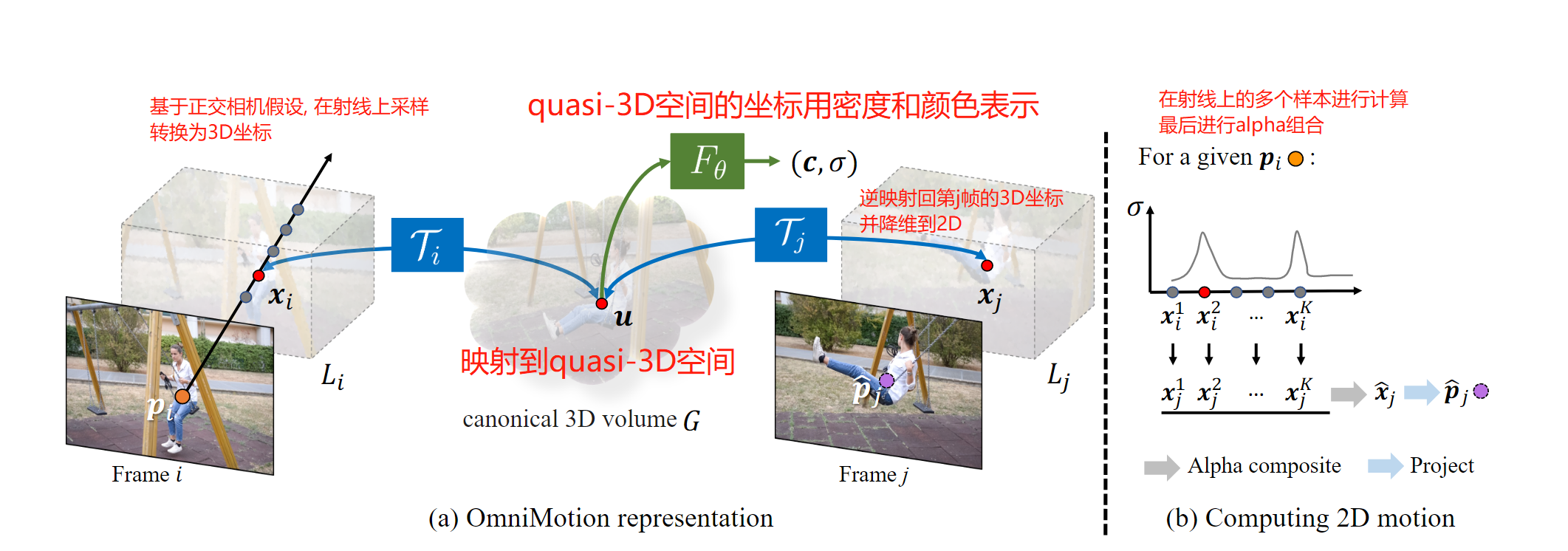
论文地址: 论文 代码地址: 代码 这是一篇效果极好的像素级跟踪的文章, 发表在ICCV2023, 可以非常好的应对遮挡等情形, 其根本的方法在于将2D点投影到一个伪3D(quasi-3D)空间, 然后再映射回去, 就可以在其他帧中得到稳定跟踪. 这篇文章的方法不是很好理解, 代码也刚开源, 做一…...
论文解读：交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架（二）
HoST框架核心实现方法详解 - 论文深度解读（第二部分） 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章： 论文深度解读 + 算法与代码分析（二） 作者机构： 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题： 人形机器人…...
python/java环境配置
环境变量放一起 python： 1.首先下载Python Python下载地址：Download Python | Python.org downloads ---windows -- 64 2.安装Python 下面两个，然后自定义，全选 可以把前4个选上 3.环境配置 1）搜高级系统设置 2…...
Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码，写上注释 当然可以！这段代码是 Qt …...
pam_env.so模块配置解析
在PAM（Pluggable Authentication Modules）配置中， /etc/pam.d/su 文件相关配置含义如下： 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块，负责验证用户身份&am…...
【论文笔记】若干矿井粉尘检测算法概述
总的来说，传统机器学习、传统机器学习与深度学习的结合、LSTM等算法所需要的数据集来源于矿井传感器测量的粉尘浓度，通过建立回归模型来预测未来矿井的粉尘浓度。传统机器学习算法性能易受数据中极端值的影响。YOLO等计算机视觉算法所需要的数据集来源于…...
JDK 17 新特性
#JDK 17 新特性 /**************** 文本块 *****************/ python/scala中早就支持，不稀奇 String json “”" { “name”: “Java”, “version”: 17 } “”"; /**************** Switch 语句 -> 表达式 *****************/ 挺好的ÿ…...
并发编程 - go版
1.并发编程基础概念 进程和线程 A. 进程是程序在操作系统中的一次执行过程，系统进行资源分配和调度的一个独立单位。B. 线程是进程的一个执行实体,是CPU调度和分派的基本单位,它是比进程更小的能独立运行的基本单位。C.一个进程可以创建和撤销多个线程;同一个进程中…...
宇树科技，改名了！
提到国内具身智能和机器人领域的代表企业，那宇树科技（Unitree）必须名列其榜。 最近，宇树科技的一项新变动消息在业界引发了不少关注和讨论，即： 宇树向其合作伙伴发布了一封公司名称变更函称，因…...
从面试角度回答Android中ContentProvider启动原理
Android中ContentProvider原理的面试角度解析，分为已启动和未启动两种场景： 一、ContentProvider已启动的情况 1. 核心流程 触发条件：当其他组件（如Activity、Service）通过ContentR…...
Oracle11g安装包
Oracle 11g安装包 适用于windows系统，64位 下载路径 oracle 11g 安装包...