如何选择合适的损失函数
目录
如何选择合适的损失函数
1、均方误差,二次损失,L2损失(Mean Square Error, Quadratic Loss, L2 Loss)
2、平均绝对误差,L1损失(Mean Absolute Error, L1 Loss)
3、MSE vs MAE (L2损失 vs L1损失)
如果离群点是会影响业务、而且是应该被检测到的异常值,那么我们应该使用MSE。L2
如果我们认为离群点仅仅代表数据损坏,那么我们应该选择MAE作为损失。L1
3、Huber Loss,平滑的平均绝对误差
为什么使用Huber Loss?
4、Log-Cosh Loss
5、Quantile Loss(分位数损失)
如何选择合适的损失函数
机器学习中的所有算法都依赖于最小化或最大化某一个函数,我们称之为“目标函数”。最小化的这组函数被称为“损失函数”。损失函数是衡量预测模型预测期望结果表现的指标。寻找函数最小值的最常用方法是“梯度下降”。把损失函数想象成起伏的山脉,梯度下降就像从山顶滑下,目的是到达山脉的最低点。
没有一个损失函数可以适用于所有类型的数据。损失函数的选择取决于许多因素,包括是否有离群点,机器学习算法的选择,运行梯度下降的时间效率,是否易于找到函数的导数,以及预测结果的置信度。这个博客的目的是帮助你了解不同的损失函数。
损失函数可以大致分为两类:分类损失(Classification Loss)和回归损失(Regression Loss)。下面这篇博文,就将重点介绍5种回归损失。
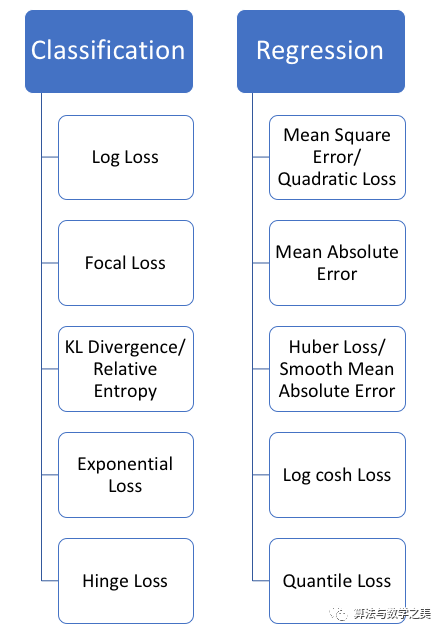
回归函数预测实数值,分类函数预测标签
▌回归损失
1、均方误差,二次损失,L2损失(Mean Square Error, Quadratic Loss, L2 Loss)
均方误差(MSE)是最常用的回归损失函数。MSE是目标变量与预测值之间距离平方之和。
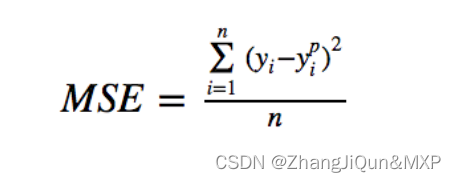
下面是一个MSE函数的图,其中真实目标值为100,预测值在-10,000至10,000之间。预测值(X轴)= 100时,MSE损失(Y轴)达到其最小值。损失范围为0至∞。
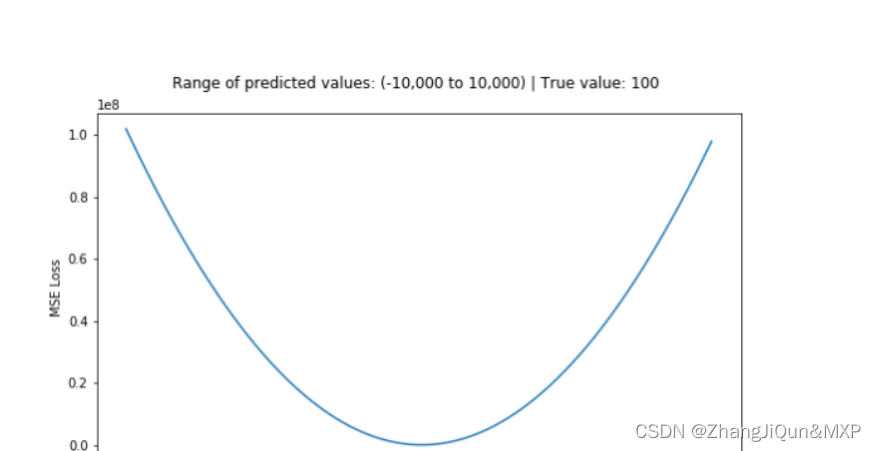
MSE损失(Y轴)与预测值(X轴)关系图
2、平均绝对误差,L1损失(Mean Absolute Error, L1 Loss)
平均绝对误差(MAE)是另一种用于回归模型的损失函数。MAE是目标变量和预测变量之间差异绝对值之和。因此,它在一组预测中衡量误差的平均大小,而不考虑误差的方向。(如果我们也考虑方向,那将被称为平均偏差(Mean Bias Error, MBE),它是残差或误差之和)。损失范围也是0到∞。
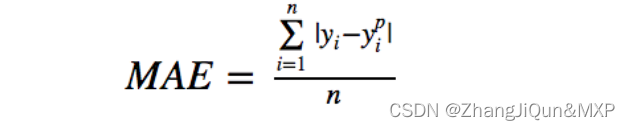
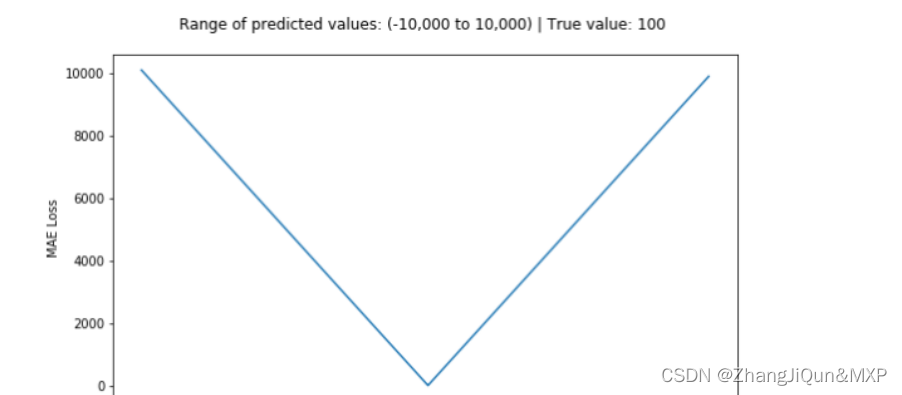
MAE损失(Y轴)与预测值(X轴)关系图
3、MSE vs MAE (L2损失 vs L1损失)
简而言之, 使用平方误差更容易求解,但使用绝对误差对离群点更加鲁棒。但是,知其然更要知其所以然!
每当我们训练机器学习模型时,我们的目标就是找到最小化损失函数的点。当然,当预测值正好等于真实值时,这两个损失函数都达到最小值。
下面让我们快速过一遍两个损失函数的Python代码。我们可以编写自己的函数或使用sklearn的内置度量函数:

#true:真正的目标变量数组
#pred:预测数组
**
def mse(true, pred):
return np.sum(((true – pred)**2))
**
def mae(true, pred):
return np.sum(np.abs(true – pred))
**
#也可以在sklearn中使用
**
from sklearn.metrics import mean_squared_error
from sklearn.metrics import mean_absolute_error
让我们来看看两个例子的MAE值和RMSE值(RMSE,Root Mean Square Error,均方根误差,它只是MSE的平方根,使其与MAE的数值范围相同)。在第一个例子中,预测值接近真实值,观测值之间误差的方差较小。第二个例子中,有一个异常观测值,误差很高。
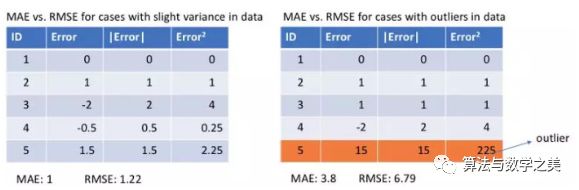
左:误差彼此接近 右:有一个误差和其他误差相差很远
我们从中观察到什么?我们该如何选择使用哪种损失函数?
由于MSE对误差(e)进行平方操作(y - y_predicted = e),如果e> 1,误差的值会增加很多。如果我们的数据中有一个离群点,e的值将会很高,将会远远大于|e|。这将使得和以MAE为损失的模型相比,以MSE为损失的模型会赋予更高的权重给离群点。在上面的第二个例子中,以RMSE为损失的模型将被调整以最小化这个离群数据点,但是却是以牺牲其他正常数据点的预测效果为代价,这最终会降低模型的整体性能。
MAE损失适用于训练数据被离群点损坏的时候(即,在训练数据而非测试数据中,我们错误地获得了不切实际的过大正值或负值)。
直观来说,我们可以像这样考虑:对所有的观测数据,如果我们只给一个预测结果来最小化MSE,那么该预测值应该是所有目标值的均值。但是如果我们试图最小化MAE,那么这个预测就是所有目标值的中位数。我们知道中位数对于离群点比平均值更鲁棒,这使得MAE比MSE更加鲁棒。
使用MAE损失(特别是对于神经网络)的一个大问题是它的梯度始终是相同的,这意味着即使对于小的损失值,其梯度也是大的。这对模型的学习可不好。为了解决这个问题,我们可以使用随着接近最小值而减小的动态学习率。MSE在这种情况下的表现很好,即使采用固定的学习率也会收敛。MSE损失的梯度在损失值较高时会比较大,随着损失接近0时而下降,从而使其在训练结束时更加精确。
决定使用哪种损失函数?
如果离群点是会影响业务、而且是应该被检测到的异常值,那么我们应该使用MSE。L2
如果我们认为离群点仅仅代表数据损坏,那么我们应该选择MAE作为损失。L1
我建议阅读下面这篇文章,其中有一项很好的研究,比较了在存在和不存在离群点的情况下使用L1损失和L2损失的回归模型的性能。请记住,L1和L2损失分别是MAE和MSE的另一个名称而已。
地址:
http://rishy.github.io/ml/2015/07/28/l1-vs-l2-loss/
L1损失对异常值更加稳健,但其导数并不连续,因此求解效率很低。L2损失对异常值敏感,但给出了更稳定的闭式解(closed form solution)(通过将其导数设置为0)
两种损失函数的问题:可能会出现这样的情况,即任何一种损失函数都不能给出理想的预测。例如,如果我们数据中90%的观测数据的真实目标值是150,其余10%的真实目标值在0-30之间。那么,一个以MAE为损失的模型可能对所有观测数据都预测为150,而忽略10%的离群情况,因为它会尝试去接近中值。同样地,以MSE为损失的模型会给出许多范围在0到30的预测,因为它被离群点弄糊涂了。这两种结果在许多业务中都是不可取的。
在这种情况下怎么做?一个简单的解决办法是转换目标变量。另一种方法是尝试不同的损失函数。这是我们的第三个损失函数——Huber Loss——被提出的动机。
3、Huber Loss,平滑的平均绝对误差
Huber Loss对数据离群点的敏感度低于平方误差损失。它在0处也可导。基本上它是绝对误差,当误差很小时,误差是二次形式的。误差何时需要变成二次形式取决于一个超参数,(delta),该超参数可以进行微调。当 𝛿 ~ 0时, Huber Loss接近MAE,当 𝛿 ~ ∞(很大的数)时,Huber Loss接近MSE。
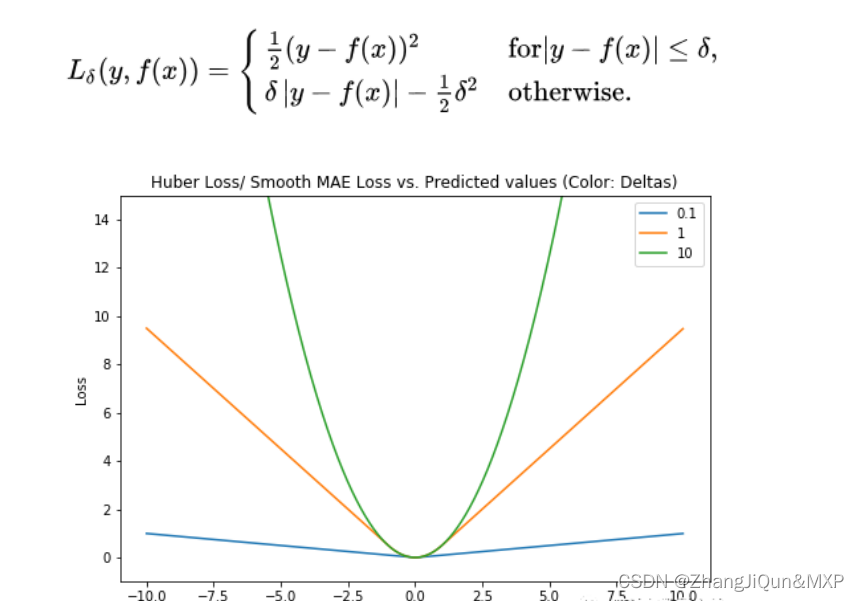
Huber Loss(Y轴)与预测值(X轴)关系图。真值= 0
delta的选择非常重要,因为它决定了你认为什么数据是离群点。大于delta的残差用L1最小化(对较大的离群点较不敏感),而小于delta的残差则可以“很合适地”用L2最小化。
为什么使用Huber Loss?
使用MAE训练神经网络的一个大问题是经常会遇到很大的梯度,使用梯度下降时可能导致训练结束时错过最小值。对于MSE,梯度会随着损失接近最小值而降低,从而使其更加精确。
在这种情况下,Huber Loss可能会非常有用,因为它会使最小值附近弯曲,从而降低梯度。另外它比MSE对异常值更鲁棒。因此,它结合了MSE和MAE的优良特性。但是,Huber Loss的问题是我们可能需要迭代地训练超参数delta。
4、Log-Cosh Loss
Log-cosh是用于回归任务的另一种损失函数,它比L2更加平滑。Log-cosh是预测误差的双曲余弦的对数。
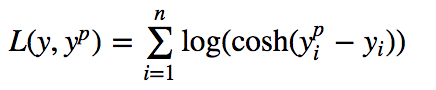
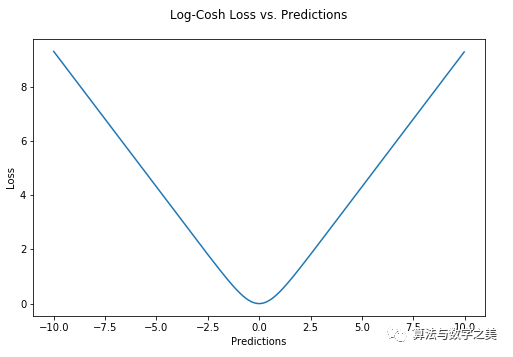
Log-cosh Loss(Y轴)与预测值(X轴)关系图。真值= 0
优点:log(cosh(x))对于小的x来说,其大约等于 (x ** 2) / 2,而对于大的x来说,其大约等于 abs(x) - log(2)。这意味着'logcosh'的作用大部分与均方误差一样,但不会受到偶尔出现的极端不正确预测的强烈影响。它具有Huber Loss的所有优点,和Huber Loss不同之处在于,其处处二次可导。
为什么我们需要二阶导数?许多机器学习模型的实现(如XGBoost)使用牛顿方法来寻找最优解,这就是为什么需要二阶导数(Hessian)的原因。对于像XGBoost这样的机器学习框架,二阶可导函数更有利。

XGBoost中使用的目标函数。注意其对一阶和二阶导数的依赖性。
但Log-chsh Loss并不完美。它仍然存在梯度和Hessian问题,对于误差很大的预测,其梯度和hessian是恒定的。因此会导致XGBoost中没有分裂。
Huber和Log-cosh损失函数的Python代码:
def sm_mae(true, pred, delta):
"""
true: array of true values
pred: array of predicted values
returns: smoothed mean absolute error loss
"""
loss = np.where(np.abs(true-pred) < delta , 0.5*((true-pred)**2), delta*np.abs(true - pred) - 0.5*(delta**2))
return np.sum(loss)
def logcosh(true, pred):
loss = np.log(np.cosh(pred - true))
return np.sum(loss)
5、Quantile Loss(分位数损失)
在大多数真实预测问题中,我们通常想了解我们预测的不确定性。了解预测值的范围而不仅仅是单一的预测点可以显着改善许多业务问题的决策过程。
当我们有兴趣预测一个区间而不仅仅是预测一个点时,Quantile Loss函数就很有用。最小二乘回归的预测区间是基于这样一个假设:残差(y - y_hat)在独立变量的值之间具有不变的方差。我们不能相信线性回归模型,因为它违反了这一假设。当然,我们也不能仅仅认为这种情况一般使用非线性函数或基于树的模型就可以更好地建模,而简单地抛弃拟合线性回归模型作为基线的想法。这时,Quantile Loss就派上用场了。因为基于Quantile Loss的回归模型可以提供合理的预测区间,即使是对于具有非常数方差或非正态分布的残差亦是如此。
让我们看一个有效的例子,以更好地理解为什么基于Quantile Loss的回归模型对异方差数据表现良好。
Quantile 回归 vs 普通最小二乘(Ordinary Least Square, OLS)回归
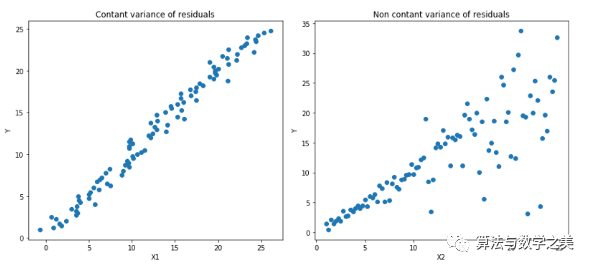
左:线性关系b/w X1和Y,残差的方差恒定。右:线性关系b/w X2和Y,但Y的方差随着X2增加而变大(异方差)。
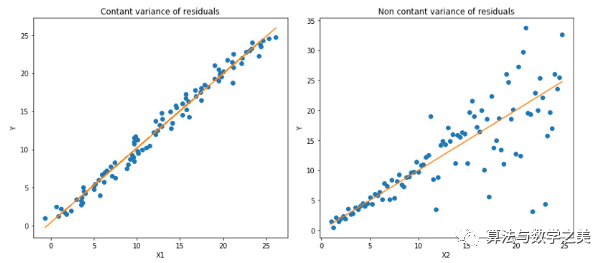
橙线表示两种情况下的OLS估计
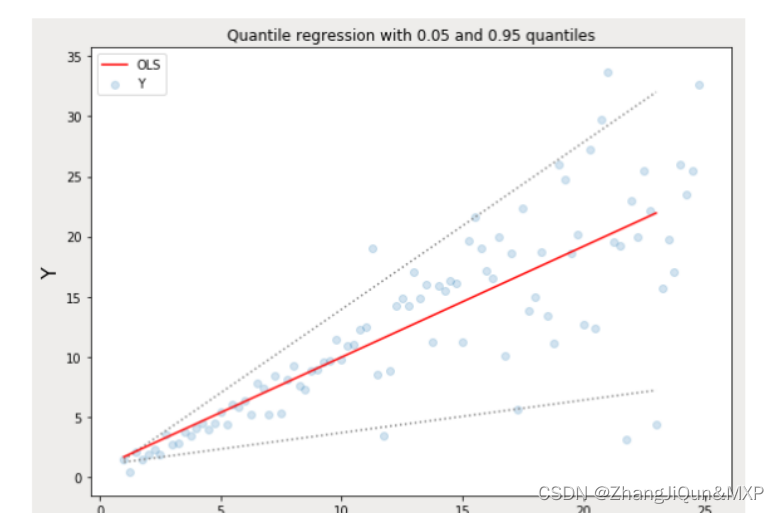
Quantile回归:虚线表示基于0.05和0.95 分位数损失函数的回归估计
如上所示的Quantile回归代码在下面这个notebook中。
地址:
https://github.com/groverpr/Machine-Learning/blob/master/notebooks/09_Quantile_Regression.ipynb
了解Quantile Loss函数
基于Quantile回归的目的是,在给定预测变量的某些值时,估计因变量的条件“分位数”。Quantile Loss实际上只是MAE的扩展形式(当分位数是第50个百分位时,Quantile Loss退化为MAE)。
Quantile Loss的思想是根据我们是打算给正误差还是负误差更多的值来选择分位数数值。损失函数根据所选quantile (γ)的值对高估和低估的预测值给予不同的惩罚值。举个例子,γ= 0.25的Quantile Loss函数给高估的预测值更多的惩罚,并试图使预测值略低于中位数。
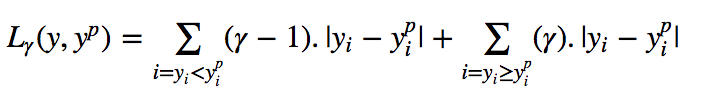
γ 是给定的分位数,其值介于0和1之间。
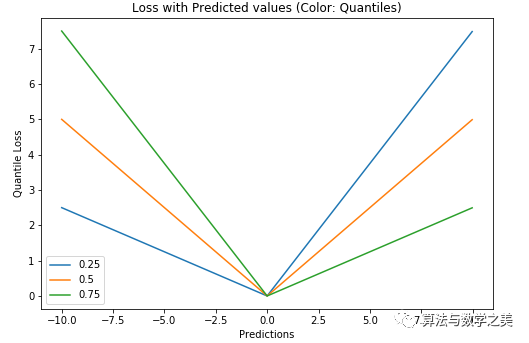
Quantile Loss(Y轴)与预测值(X轴)关系图。真值为Y= 0
我们也可以使用这个损失函数来计算神经网络或基于树的模型的预测区间。下图是sklearn实现的梯度提升树回归。
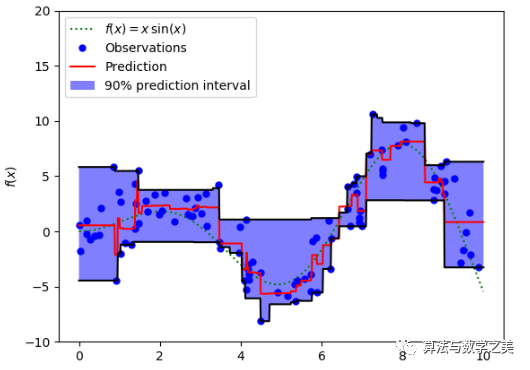
使用Quantile Loss的预测区间(梯度提升回归)
上图显示的是sklearn库的GradientBoostingRegression中的quantile loss函数计算的90%预测区间。上限的计算使用了γ = 0.95,下限则是使用了γ = 0.05。
比较研究
“Gradient boosting machines, a tutorial”中提供了一个很好的比较研究。为了演示上述所有的损失函数的性质,研究人员创造了一个人工数据集,数据集从sinc(x)函数中采样,其中加入了两种人造模拟噪声:高斯噪声分量和脉冲噪声分量。脉冲噪声项是用来展示结果的鲁棒效果的。以下是使用不同损失函数来拟合GBM(Gradient Boosting Machine, 梯度提升回归)的结果。
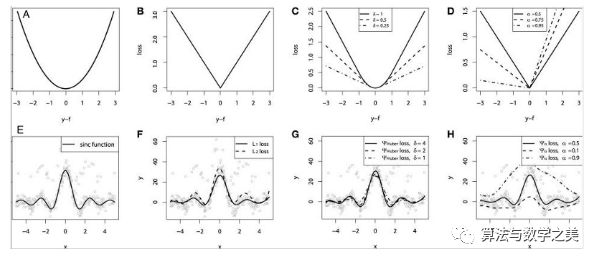
连续损失函数:(A)MSE损失函数; (B)MAE损失函数; (C)Huber损失函数; (D)Quantile损失函数。用有噪声的sinc(x)数据来拟合平滑GBM的示例:(E)原始sinc(x)函数; (F)以MSE和MAE为损失拟合的平滑GBM; (G)以Huber Loss拟合的平滑GBM, = {4,2,1}; (H)以Quantile Loss拟合的平滑GBM。
模拟实验中的一些观察结果:
-
以MAE为损失的模型预测较少受到脉冲噪声的影响,而以MSE为损失的模型的预测由于脉冲噪声造成的数据偏离而略有偏差。
-
以Huber Loss为损失函数的模型,其预测对所选的超参数不太敏感。
-
Quantile Loss对相应的置信水平给出了很好的估计。
一张图画出所有损失函数
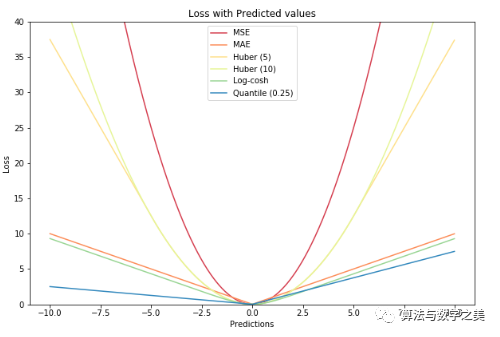
相关文章:

如何选择合适的损失函数
目录 如何选择合适的损失函数 1、均方误差,二次损失,L2损失(Mean Square Error, Quadratic Loss, L2 Loss) 2、平均绝对误差,L1损失(Mean Absolute Error, L1 Loss) 3、MSE vs MAE ÿ…...
Java常见的排序算法
排序分为内部排序和外部排序(外部存储) 常见的七大排序,这些都是内部排序 。 1、插入排序:直接插入排序 1、插入排序:每次将一个待排序的记录,按其关键字的大小插入到前面已排序好的记录序列 中的适当位置…...

【C++】5、构建:CMake
文章目录 一、概述二、实战2.1 内部构建、外部构建2.2 CLion Cmake 一、概述 CMake 是跨平台构建工具,其通过 CMakeLists.txt 描述,并生成 native 编译配置文件: 在 Linux/Unix 平台,生成 makefile在苹果平台,可以生…...
【ARP欺骗】嗅探流量、限速、断网操作
【ARP欺骗】 什么是ARP什么是ARP欺骗ARP欺骗实现ARP断网限制网速嗅探流量 什么是ARP ARP(Address Resolution Protocol,地址解析协议)是一个TCP/IP协议,用于根据IP地址获取物理地址。在计算机网络中,当一个主机需要发…...

初步认识OSPF的大致内容(第三课)
1 路由的分类 直连路由(Directly Connected Route)是指网络拓扑结构中相邻两个网络设备直接相连的路由,也称为直接路由。如果两个设备属于同一IP网络地址,那么它们就是直连设备。直连路由表是指由计算机系统生成的一种用于路由选择的表格,其中记录着直连路由的信息。直连…...
CSDN编程题-每日一练(2023-08-27)
CSDN编程题-每日一练(2023-08-27) 一、题目名称:异或和二、题目名称:生命进化书三、题目名称:熊孩子拜访 一、题目名称:异或和 时间限制:1000ms内存限制:256M 题目描述: …...

机器视觉之平面物体检测
平面物体检测是计算机视觉中的一个重要任务,它通常涉及检测和识别在图像或视频中出现的平面物体,如纸张、标志、屏幕、牌子等。下面是一个使用C和OpenCV进行平面物体检测的简单示例,使用了图像中的矩形轮廓检测方法: #include &l…...
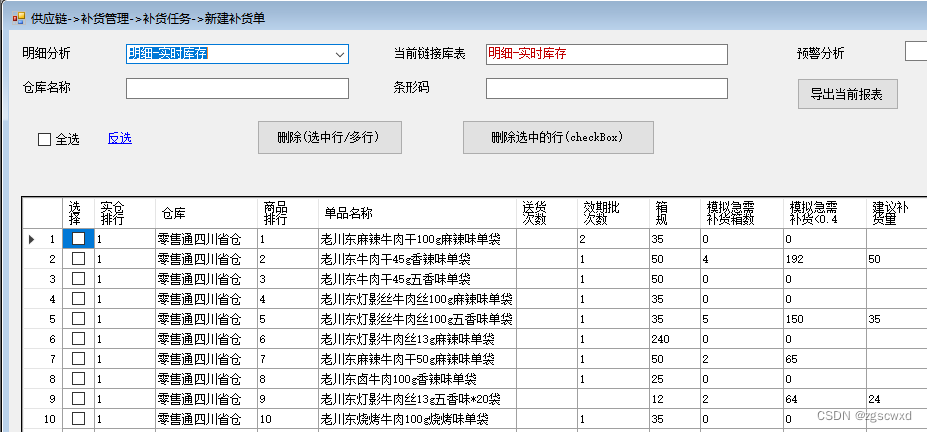
C#开发WinForm之DataGridView开发
前言 DataGridView是开发Winform的一个列表展示,类似于表格。学会下面的基本特征用法,再辅以经验,基本功能开发没问题。 1.设置 DataGridView表格行首为序号索引, //设置 DataGridView表格行首为序号索引private void dataGridView1_RowPost…...
PDFPrinting.Net Crack
PDFPrinting.Net Crack 它能够轻松灵活地预测完美的打印结果以及用户文件的示例性显示。在.NET的PDF打印中,可以快速浏览最关键的元素。如果用户需要获得更详细的概述,那么他可以查看快速入门手册,甚至现有文档的详细概述参考。 在这种情况下…...
git操作:将一个仓库的分支提交到另外一个仓库分支
这个操作,一般是同步不同网站的同个仓库,比如说gitee 和github。某个网站更新了,你想同步他的分支过来。然后基于分支开发或者其它。 操作步骤 1.本地先clone 你自己的仓库。也就是要push 分支的仓库。比如A仓库,把B仓库分支&am…...
基于Java+SpringBoot+Vue前后端分离医院资源管理系统设计和实现
博主介绍:✌全网粉丝30W,csdn特邀作者、博客专家、CSDN新星计划导师、Java领域优质创作者,博客之星、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 🍅文末获取源码联系🍅 👇🏻 精彩专…...
Android——基本控件下(十七)
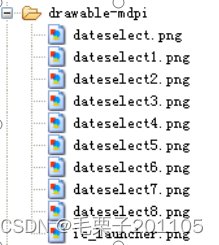
1. 文本切换:TextSwitcher 1.1 知识点 (1)理解TextSwitcher和ViewFactory的使用。 1.2 具体内容 范例:切换显示当前时间 <LinearLayout xmlns:android"http://schemas.android.com/apk/res/android"xmlns:tools&…...
HCIP-HCS华为私有云
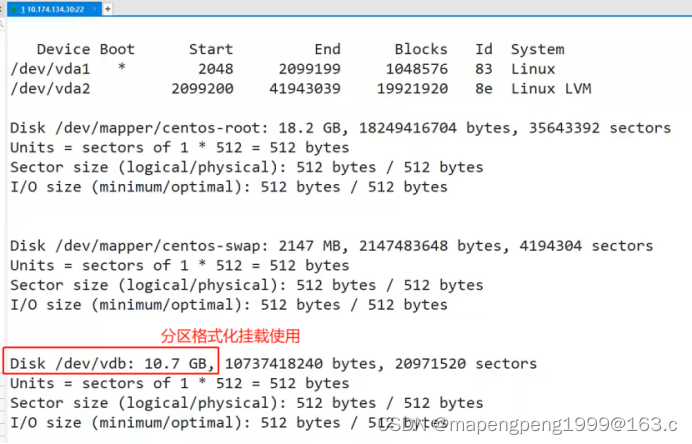
1、概述 HCS(HuaweiCoudStack)华为私有云:6.3 之前叫FusionSphere OpenStack,6.3.1 版本开始叫FusionCloud,6.5.1 版本开始叫HuaweiCloud Stack (HCS)华为私有云软件。 开源openstack,发放云主机的流程&am…...

docker下载github项目失败
Docker 在构建过程中直接从 GitHub 下载项目时超时,可能是由于网络问题、GitHub 访问限制或其他原因导致的。以下是一些建议和解决方法: 预先下载项目: 在构建 Docker 镜像之前,首先在宿主机上手动克隆 GitHub 项目,然后使用 COPY…...
【CSS】网站 网格商品展示 模块制作 ( 清除浮动需求 | 没有设置高度的盒子且内部设置了浮动 | 使用双伪元素清除浮动 )
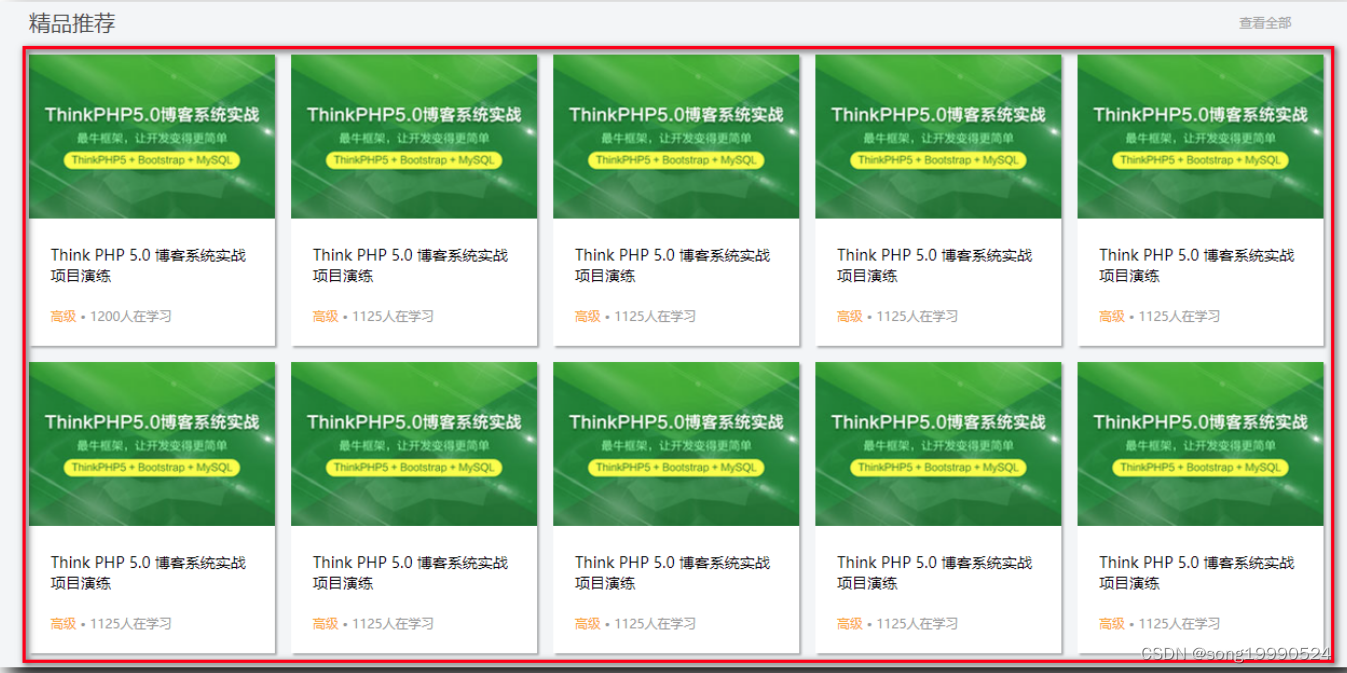
一、清除浮动需求 ( 没有设置高度的盒子且内部设置了浮动 ) 绘制的如下模块 : 在上面的盒子中 , 没有设置高度 , 只设置了一个 1215px 的宽度 ; 在列表中每个列表项都设置了 浮动 ; /* 网格商品展示 */ .box-bd {/* 处理列表间隙导致意外换行问题一排有 5 个 228x270 的盒子…...

文本分类任务
文章目录 引言1. 文本分类-使用场景2. 自定义类别任务3. 贝叶斯算法3.1 预备知识3.2 贝叶斯公式3.3 贝叶斯公式的应用3.4 贝叶斯公式在NLP中的应用3.5 贝叶斯公式-文本分类3.6 代码实现3.7 贝叶斯算法的优缺点 4. 支持向量机4.1 支持向量机-核函数4.2 支持向量机-解决多分类4.3…...
:Python中的pyecharts库绘制3D曲面图)
Pyecharts教程(一):Python中的pyecharts库绘制3D曲面图
Pyecharts教程(一):Python中的pyecharts库绘制3D曲面图 作者:安静到无声 个人主页 目录 Pyecharts教程(一):Python中的pyecharts库绘制3D曲面图实验结果推荐专栏在Python中,我们可以使用pyecharts库来绘制各种图表,如柱状图、折线图、饼图等。最近,我在学习如何使用pyec…...

Unity音频基础概念
一、音源与音频侦听器 游戏画面能够被观众看到,是因为有渲染器和摄像机,同样音频能够被听到,也要有声音的发出者与声音的接收者。声音的发出者叫做音源,接收者叫做音频侦听器。Audio Source与Audio Listener都是组件,…...

sklearn Preprocessing 数据预处理功能
scikit-learn(或sklearn)的数据预处理模块提供了一系列用于处理和准备数据的工具。这些工具可以帮助你在将数据输入到机器学习模型之前对其进行预处理、清洗和转换。以下是一些常用的sklearn.preprocessing模块中的类和功能: 1. 数据缩放和中…...
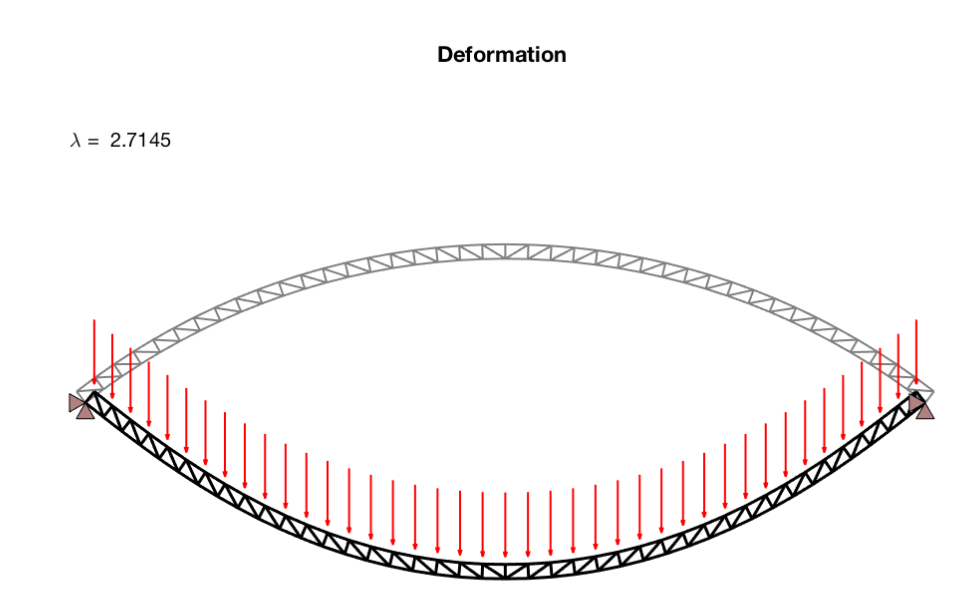
创建和分析二维桁架和梁结构研究(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

idea大量爆红问题解决
问题描述 在学习和工作中,idea是程序员不可缺少的一个工具,但是突然在有些时候就会出现大量爆红的问题,发现无法跳转,无论是关机重启或者是替换root都无法解决 就是如上所展示的问题,但是程序依然可以启动。 问题解决…...
)
React Native 开发环境搭建(全平台详解)
React Native 开发环境搭建(全平台详解) 在开始使用 React Native 开发移动应用之前,正确设置开发环境是至关重要的一步。本文将为你提供一份全面的指南,涵盖 macOS 和 Windows 平台的配置步骤,如何在 Android 和 iOS…...

2025年能源电力系统与流体力学国际会议 (EPSFD 2025)
2025年能源电力系统与流体力学国际会议(EPSFD 2025)将于本年度在美丽的杭州盛大召开。作为全球能源、电力系统以及流体力学领域的顶级盛会,EPSFD 2025旨在为来自世界各地的科学家、工程师和研究人员提供一个展示最新研究成果、分享实践经验及…...

Swift 协议扩展精进之路:解决 CoreData 托管实体子类的类型不匹配问题(下)
概述 在 Swift 开发语言中,各位秃头小码农们可以充分利用语法本身所带来的便利去劈荆斩棘。我们还可以恣意利用泛型、协议关联类型和协议扩展来进一步简化和优化我们复杂的代码需求。 不过,在涉及到多个子类派生于基类进行多态模拟的场景下,…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

现代密码学 | 椭圆曲线密码学—附py代码
Elliptic Curve Cryptography 椭圆曲线密码学(ECC)是一种基于有限域上椭圆曲线数学特性的公钥加密技术。其核心原理涉及椭圆曲线的代数性质、离散对数问题以及有限域上的运算。 椭圆曲线密码学是多种数字签名算法的基础,例如椭圆曲线数字签…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

今日科技热点速览
🔥 今日科技热点速览 🎮 任天堂Switch 2 正式发售 任天堂新一代游戏主机 Switch 2 今日正式上线发售,主打更强图形性能与沉浸式体验,支持多模态交互,受到全球玩家热捧 。 🤖 人工智能持续突破 DeepSeek-R1&…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...
