排序算法:归并排序
约翰·冯·诺伊曼在 1945 年提出了归并排序。在讲解归并排序之前,我们先一起思考一个问题:如何将两个有序的列表合并成一个有序的列表?
将两个有序的列表合并成一个有序的列表
这太简单了,笔者首先想到的思路就是,将两个列表拼接成一个列表,然后之前学的冒泡、选择、插入、希尔、堆、快排都可以派上用场了。
觉得太暴力了一点?那我们换个思路。
既然列表已经有序了,通过前几章的学习,我们已经知道,插入排序的过程中,被插入的数组也是有序的。这就好办了,我们将其中一个列表中的元素逐个插入另一个列表中即可。
但是按照这个思路,我们只需要一个列表有序就行了,另一个列表不管是不是有序的,都会被逐个取出来,插入第一个列表中。那么,在两个列表都已经有序的情况下,还可以有更优的合并方案吗?
深入思考之后,我们发现,在第二个列表向第一个列表逐个插入的过程中,由于第二个列表已经有序,所以后续插入的元素一定不会在前面插入的元素之前。在逐个插入的过程中,每次插入时,只需要从上次插入的位置开始,继续向后寻找插入位置即可。这样一来,我们最多只需要将两个有序数组遍历一次就可以完成合并。
思路很接近了,如何实现它呢?我们发现,在向数组中不断插入新数字时,原数组需要不断腾出位置,这是一个比较复杂的过程,而且这个过程必然导致增加一轮遍历。
但好在我们有一个替代方案:只要开辟一个长度等同于两个数组长度之和的新数组,并使用两个指针来遍历原有的两个数组,不断将较小的数字添加到新数组中,并移动对应的指针即可。
根据这个思路,我们可以写出合并两个有序列表的代码:
// 将两个有序数组合并为一个有序数组
private static int[] merge(int[] arr1, int[] arr2) {int[] result = new int[arr1.length + arr2.length];int index1 = 0, index2 = 0;while (index1 < arr1.length && index2 < arr2.length) {if (arr1[index1] <= arr2[index2]) {result[index1 + index2] = arr1[index1];index1++;} else {result[index1 + index2] = arr2[index2];index2++;}}// 将剩余数字补到结果数组之后while (index1 < arr1.length) {result[index1 + index2] = arr1[index1];index1++;}while (index2 < arr2.length) {result[index1 + index2] = arr2[index2];index2++;}return result;
}这份代码的实现思路和我们分析的一模一样:首先开辟了一个新数组 result,长度等同于 arr1 和 arr2 的长度之和,然后使用 index1 记录 arr1 数组的下标,index2 记录 arr2 数组的下标。再将两个数组中较小的值不断添加到 result 中。其中,result 的当前下标等同于 index1 和 index2 之和。
如果你对 ++ 运算符用得熟练的话:
result[index1 + index2] = arr1[index1];
index1++;可以简写成:
result[index1 + index2] = arr1[index1++];这样代码看起来会更简洁一些。
合并有序数组的问题解决了,但我们排序时用的都是无序数组,那么上哪里去找这两个有序的数组呢?
答案是 —— 自己拆分,我们可以把数组不断地拆成两份,直到只剩下一个数字时,这一个数字组成的数组我们就可以认为它是有序的。
然后通过上述合并有序列表的思路,将 1 个数字组成的有序数组合并成一个包含 2 个数字的有序数组,再将 2 个数字组成的有序数组合并成包含 4 个数字的有序数组...直到整个数组排序完成,这就是归并排序(Merge Sort)的思想。
将数组拆分成有序数组
拆分过程使用了二分的思想,这是一个递归的过程,归并排序使用的递归框架如下:
public static void mergeSort(int[] arr) {if (arr.length == 0) return;int[] result = mergeSort(arr, 0, arr.length - 1);// 将结果拷贝到 arr 数组中for (int i = 0; i < result.length; i++) {arr[i] = result[i];}
}// 对 arr 的 [start, end] 区间归并排序
private static int[] mergeSort(int[] arr, int start, int end) {// 只剩下一个数字,停止拆分,返回单个数字组成的数组if (start == end) return new int[]{arr[start]};int middle = (start + end) / 2;// 拆分左边区域int[] left = mergeSort(arr, start, middle);// 拆分右边区域int[] right = mergeSort(arr, middle + 1, end);// 合并左右区域return merge(left, right);
}其中, mergeSort(int[] arr) 函数是对外暴露的公共方法,内部调用了私有的mergeSort(int[] arr, int start, int end) 函数,这个函数用于对 arr 的 [start, end] 区间进行归并排序。可以看到,我们在这个函数中,将原有数组不断地二分,直到只剩下最后一个数字。此时嵌套的递归开始返回,一层层地调用merge(int[] arr1, int[] arr2)函数,也就是我们刚才写的将两个有序数组合并为一个有序数组的函数。这就是最经典的归并排序,只需要一个二分拆数组的递归函数和一个合并两个有序列表的函数即可。但这份代码还有一个缺点,那就是在递归过程中,开辟了很多临时空间,接下来我们就来看下它的优化过程。
归并排序的优化:减少临时空间的开辟
为了减少在递归过程中不断开辟空间的问题,我们可以在归并排序之前,先开辟出一个临时空间,在递归过程中统一使用此空间进行归并即可。
代码如下:
public static void mergeSort(int[] arr) {if (arr.length == 0) return;int[] result = new int[arr.length];mergeSort(arr, 0, arr.length - 1, result);
}// 对 arr 的 [start, end] 区间归并排序
private static void mergeSort(int[] arr, int start, int end, int[] result) {// 只剩下一个数字,停止拆分if (start == end) return;int middle = (start + end) / 2;// 拆分左边区域,并将归并排序的结果保存到 result 的 [start, middle] 区间mergeSort(arr, start, middle, result);// 拆分右边区域,并将归并排序的结果保存到 result 的 [middle + 1, end] 区间mergeSort(arr, middle + 1, end, result);// 合并左右区域到 result 的 [start, end] 区间merge(arr, start, end, result);
}// 将 result 的 [start, middle] 和 [middle + 1, end] 区间合并
private static void merge(int[] arr, int start, int end, int[] result) {int middle = (start + end) / 2;// 数组 1 的首尾位置int start1 = start;int end1 = middle;// 数组 2 的首尾位置int start2 = middle + 1;int end2 = end;// 用来遍历数组的指针int index1 = start1;int index2 = start2;// 结果数组的指针int resultIndex = start1;while (index1 <= end1 && index2 <= end2) {if (arr[index1] <= arr[index2]) {result[resultIndex++] = arr[index1++];} else {result[resultIndex++] = arr[index2++];}}// 将剩余数字补到结果数组之后while (index1 <= end1) {result[resultIndex++] = arr[index1++];}while (index2 <= end2) {result[resultIndex++] = arr[index2++];}// 将 result 操作区间的数字拷贝到 arr 数组中,以便下次比较for (int i = start; i <= end; i++) {arr[i] = result[i];}
}在这份代码中,我们统一使用 result 数组作为递归过程中的临时数组,所以merge 函数接收的参数不再是两个数组,而是 result 数组中需要合并的两个数组的首尾下标。根据首尾下标可以分别计算出两个有序数组的首尾下标 start1、end1、start2、end2,之后的过程就和之前合并两个有序数组的代码类似了。
这份代码还可以再精简一下,我们可以去掉一些不会改变的临时变量。比如 start1 始终等于 start,end2 始终等于 end,end1 始终等于 middle。并且分析可知,resultIndex 的值始终等于 start 加上 index1 和 index2 移动的距离。即:
resultIndex = start + (index1 - start1) + (index2 - start2)将 start1 == start 代入,化简得:
resultIndex = index1 + index2 - start2所以最终的归并排序代码如下:
public static void mergeSort(int[] arr) {if (arr.length == 0) return;int[] result = new int[arr.length];mergeSort(arr, 0, arr.length - 1, result);
}// 对 arr 的 [start, end] 区间归并排序
private static void mergeSort(int[] arr, int start, int end, int[] result) {// 只剩下一个数字,停止拆分if (start == end) return;int middle = (start + end) / 2;// 拆分左边区域,并将归并排序的结果保存到 result 的 [start, middle] 区间mergeSort(arr, start, middle, result);// 拆分右边区域,并将归并排序的结果保存到 result 的 [middle + 1, end] 区间mergeSort(arr, middle + 1, end, result);// 合并左右区域到 result 的 [start, end] 区间merge(arr, start, end, result);
}// 将 result 的 [start, middle] 和 [middle + 1, end] 区间合并
private static void merge(int[] arr, int start, int end, int[] result) {int end1 = (start + end) / 2;int start2 = end1 + 1;// 用来遍历数组的指针int index1 = start;int index2 = start2;while (index1 <= end1 && index2 <= end) {if (arr[index1] <= arr[index2]) {result[index1 + index2 - start2] = arr[index1++];} else {result[index1 + index2 - start2] = arr[index2++];}}// 将剩余数字补到结果数组之后while (index1 <= end1) {result[index1 + index2 - start2] = arr[index1++];}while (index2 <= end) {result[index1 + index2 - start2] = arr[index2++];}// 将 result 操作区间的数字拷贝到 arr 数组中,以便下次比较while (start <= end) {arr[start] = result[start++];}
}
原地归并排序?
现在的归并排序看起来仍"美中不足",那就是仍然需要开辟额外的空间,能不能实现不开辟额外空间的归并排序呢?好像是可以做到的。在一些文章中,将这样的归并排序称之为 In-Place Merge Sort,直译为原地归并排序。
代码实现思路主要有两种:
public static void mergeSort(int[] arr) {if (arr.length == 0) return;mergeSort(arr, 0, arr.length - 1);
}// 对 arr 的 [start, end] 区间归并排序
private static void mergeSort(int[] arr, int start, int end) {// 只剩下一个数字,停止拆分if (start == end) return;int middle = (start + end) / 2;// 拆分左边区域mergeSort(arr, start, middle);// 拆分右边区域mergeSort(arr, middle + 1, end);// 合并左右区域merge(arr, start, end);
}// 将 arr 的 [start, middle] 和 [middle + 1, end] 区间合并
private static void merge(int[] arr, int start, int end) {int end1 = (start + end) / 2;int start2 = end1 + 1;// 用来遍历数组的指针int index1 = start;int index2 = start2;while (index1 <= end1 && index2 <= end) {if (arr[index1] <= arr[index2]) {index1++;} else {// 右边区域的这个数字比左边区域的数字小,于是它站了起来int value = arr[index2];int index = index2;// 前面的数字不断地后移while (index > index1) {arr[index] = arr[index - 1];index--;}// 这个数字坐到 index1 所在的位置上arr[index] = value;// 更新所有下标,使其前进一格index1++;index2++;end1++;}}
}这段代码在合并 arr 的 [start, middle] 区间和 [middle + 1, end] 区间时,将两个区间较小的数字移动到 index1 的位置,并且将左边区域不断后移,目的是给新插入的数字腾出位置。最后更新两个区间的下标,继续合并更新后的区间。
第二种实现思路:
public static void mergeSort(int[] arr) {if (arr.length == 0) return;mergeSort(arr, 0, arr.length - 1);
}// 对 arr 的 [start, end] 区间归并排序
private static void mergeSort(int[] arr, int start, int end) {// 只剩下一个数字,停止拆分if (start == end) return;int middle = (start + end) / 2;// 拆分左边区域mergeSort(arr, start, middle);// 拆分右边区域mergeSort(arr, middle + 1, end);// 合并左右区域merge(arr, start, end);
}// 将 arr 的 [start, middle] 和 [middle + 1, end] 区间合并
private static void merge(int[] arr, int start, int end) {int end1 = (start + end) / 2;int start2 = end1 + 1;// 用来遍历数组的指针int index1 = start;while (index1 <= end1 && start2 <= end) {if (arr[index1] > arr[start2]) {// 将 index1 和 start2 下标的数字交换exchange(arr, index1, start2);if (start2 != end) {// 调整交换到 start2 上的这个数字的位置,使右边区域继续保持有序int value = arr[start2];int index = start2;// 右边区域比 arr[start2] 小的数字不断前移while (index < end && arr[index + 1] < value) {arr[index] = arr[index + 1];index++;}// 交换到右边区域的这个数字找到了自己合适的位置,坐下arr[index] = value;}}index1++;}
}private static void exchange(int[] arr, int i, int j) {int temp = arr[i];arr[i] = arr[j];arr[j] = temp;
}
这段代码在合并区间时,同样是将两个区间中较小的数字移到 index1 的位置,不过采用的是两个区间的首个数字直接交换的思路,交换完成后,将交换到右边区间的数字不断后移,以使得右边区间继续保持有序。
这两种思路看起来都很美好,但这真的实现了原地归并排序吗?
分析代码可以看出,这样实现的归并本质上是插入排序!前文已经说到,在插入排序中,腾出位置是一个比较复杂的过程,而且这个过程必然导致增加一轮遍历。在这两份代码中,每一次合并数组时,都使用了两层循环,目的就是不断腾挪位置以插入新数字,可以看出这里合并的效率是非常低的。这两种排序算法的时间复杂度都达到了 (On²) 级,不能称之为归并排序。它们只是借用了归并排序的递归框架而已。
也就是说,所谓的原地归并排序事实上并不存在,许多算法书籍中都没有收录这种算法。它打着归并排序的幌子,卖的是插入排序的思想,实际排序效率比归并排序低得多。
时间复杂度 & 空间复杂度
归并排序的复杂度比较容易分析,拆分数组的过程中,会将数组拆分 logn 次,每层执行的比较次数都约等于 n 次,所以时间复杂度是 O(nlogn)。
空间复杂度是 O(n),主要占用空间的就是我们在排序前创建的长度为 n 的 result 数组。
分析归并的过程可知,归并排序是一种稳定的排序算法。其中,对算法稳定性非常重要的一行代码是:
if (arr[index1] <= arr[index2]) {result[index1 + index2 - start2] = arr[index1++];
}在这里我们通过arr[index1] <= arr[index2]来合并两个有序数组,保证了原数组中,相同的元素相对顺序不会变化,如果这里的比较条件写成了arr[index1] < arr[index2],则归并排序将变得不稳定。
总结起来,归并排序分成两步,一是拆分数组,二是合并数组,它是分治思想的典型应用。分治的意思是“分而治之”,分的时候体现了二分的思想,“一尺之棰,日取其半,logn 世竭”,治是一个滚雪球的过程,将 1 个数字组成的有序数组合并成一个包含 2 个数字的有序数组,再将 2 个数字组成的有序数组合并成包含 4 个数字的有序数组...如《活着》一书中的经典名句:“小鸡长大了就变成了鹅;鹅长大了,就变成了羊;羊再长大了,就变成了牛...”
由于性能较好,且排序稳定,归并排序应用非常广泛,Arrays.sort() 源码中的 TimSort就是归并排序的优化版。
相关文章:

排序算法:归并排序
约翰冯诺伊曼在 1945 年提出了归并排序。在讲解归并排序之前,我们先一起思考一个问题:如何将两个有序的列表合并成一个有序的列表? 将两个有序的列表合并成一个有序的列表 这太简单了,笔者首先想到的思路就是,将两个列…...

Hbase-技术文档-spring-boot整合使用hbase--简单操作增删改查--提供封装高可用的模版类
使用spring-boot项目来整合使用hbase。 引入依赖 <dependency><groupId>org.apache.hbase</groupId><artifactId>hbase-client</artifactId><version>2.4.3</version> </dependency> 依赖声明表示将把Apache HBase客户端库…...
基于Pytorch的神经网络部分自定义设计
一、基础概念(学习笔记) (1)训练误差和泛化误差[1] 本质上,优化和深度学习的目标是根本不同的。前者主要关注的是最小化目标,后者则关注在给定有限数据量的情况下寻找合适的模型。训练误差和泛化误差通常不…...

持续更新串联记忆English words
(一)这是一组关于“服装搭配”的单词。通过在记忆中检索,回忆起隐藏的信息吧~ >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>今日单词>>&…...

postgresql 内核源码分析 btree索引的增删查代码基本原理流程分析,索引膨胀的原因在这里
B-Tree索引代码流程分析 专栏内容: postgresql内核源码分析手写数据库toadb并发编程 开源贡献: toadb开源库 个人主页:我的主页 管理社区:开源数据库 座右铭:天行健,君子以自强不息;地势坤&…...

详细了解G1、了解G1、G1垃圾收集器详解、G1垃圾回收器简单调优
4.详细了解G1: 4.1.一:什么是垃圾回收 4.2.了解G1 4.3.G1 Yong GC 4.4.G1 Mix GC 4.5.三色标记算法 4.6.调优实践 5.G1垃圾收集器详解 5.1.G1垃圾收集器 5.2.G1的堆内存划分 5.3.G1的运行过程 5.4.三色标记 5.4.1.漏标问题 5.5.记忆集与卡表 5.6.安全点与…...

vue项目中 package.json 详解
在 Vue 项目中,package.json 是一个重要的配置文件,它包含了项目的名称、版本、作者、依赖等信息。下面是一份详细的 Vue 项目 package.json 配置说明: 1.name:项目的名称,用于标识项目,例如:&q…...

为什么要进行管网水位监测,管网水位监测的作用是什么
管网水位监测是城市排水系统管理的重要手段,对于保障城市排水设施安全运行和提升城市管理水平具有重要意义。通过对排水管网的水位进行实时监测和分析,能够及时发现问题并采取措施,提高排水系统的运行效率和管理水平。本文将详细介绍为什么要…...

webpack学习笔记
1. webpack基本概念 webpack: JavaScript 应用程序的静态模块打包器,是目前最为流行的JavaScript打包工具之一。webpack会以一个或多个js文件为入口,递归检查每个js模块的依赖,从而构建一个依赖关系图,然后依据该关系…...

解析代理IP在跨境电商和社媒营销中的关键作用
跨境电商和社媒营销领域的从业者深知,代理IP的价值愈发凸显。在推广营销的过程中,频繁遇到因IP关联而封禁账号的情况,或因使用不安全IP而导致异常问题。 这些问题促使人们开始高度重视代理IP的作用。但实际上,代理IP究竟是何物&a…...

Unity 之 Start 与Update 方法的区别
文章目录 当谈论Unity中的 Start和 Update方法时,我们实际上是在讨论MonoBehaviour类中的两个常用方法,用于编写游戏逻辑。这两个方法在不同的时机被调用,因此您可以根据需要选择在哪个方法中编写特定的代码。 Start 方法: Start…...

Spring Boot中如何编写优雅的单元测试
单元测试是指对软件中的最小可测试单元进行检查和验证。在Java中,单元测试的最小单元是类。通过编写针对类或方法的小段代码,来检验被测代码是否符合预期结果或行为。执行单元测试可以帮助开发者验证代码是否正确实现了功能需求,以及是否能够…...
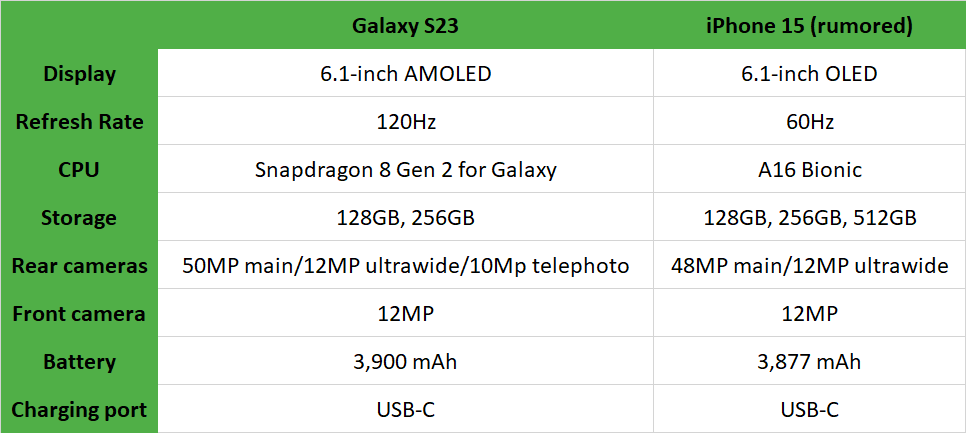
三星Galaxy S23与iPhone 15的对比分析:谁会胜出?
三星Galaxy S23与iPhone 15的对决将于下个月进入高潮,这将是今年智能手机中最大的一场较量。毕竟,这是两家领先的移动设备制造商的旗舰手机。他们的手机的比较将在很大程度上决定谁能获得最佳手机的称号。 我们已经知道有利于三星Galaxy S23的情况,该产品自春季以来一直在推…...

MySQL索引 事物 存储引擎
一 索引 索引的概念 索引就是一种帮助系统能够更快速的查找信息的结构 索引的作用 索引的副作用 创建索引的规则 MySQL的优化 哪些字段/场景适合创建索引 哪些不适合 小字段唯一性强的字段更新不频繁,但查询率比较高的字段表记录超过 300行主键,外键…...

【谷粒学院】报错记录
无法从Nacos获取动态配置 原先gulimall-common中SpringCloud Alibaba的版本是2.1.0.RELEASE,无法从Nacos中获取配置文件信息 <dependencyManagement><dependencies><dependency><groupId>com.alibaba.cloud</groupId><artifactId&…...

微积分基本概念
微分 函数的微分是指对函数的局部变化的一种线性描述。微分可以近似地描述当函数自变量的取值作足够小的改变时,函数的值是怎样改变的。。对于函数 y f ( x ) y f(x) yf(x) 的微分记作: d y f ′ ( x ) d x d_y f^{}(x)d_x dyf′(x)dx 微分和…...
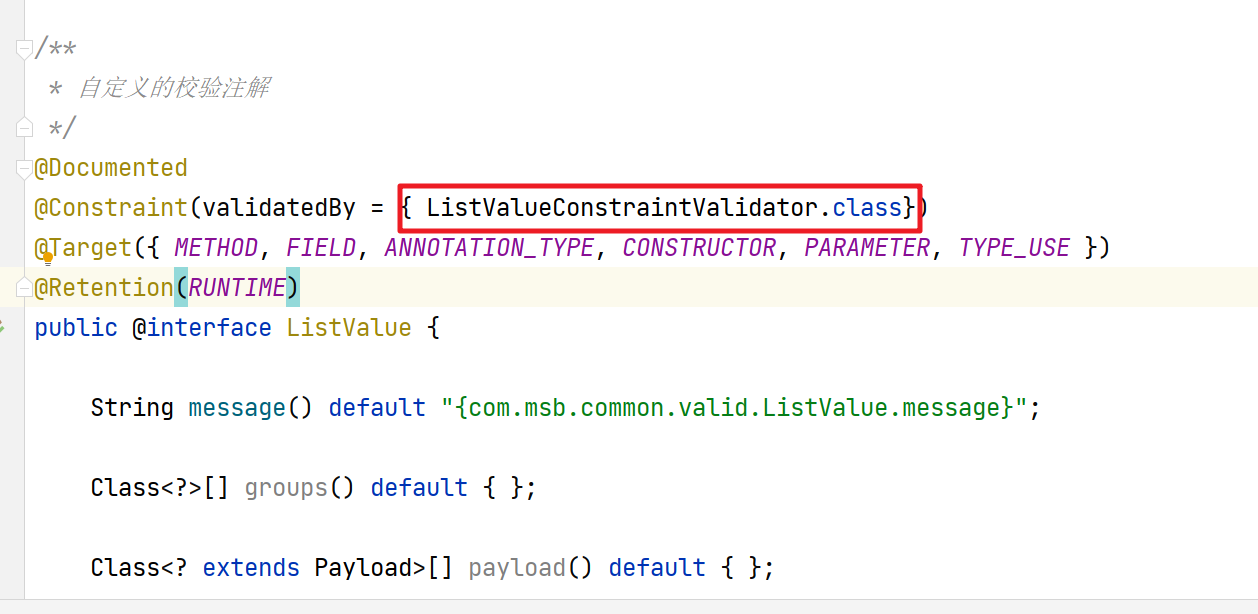
【业务功能篇78】微服务-前端后端校验- 统一异常处理-JSR-303-validation注解
5. 前端校验 我们在前端提交的表单数据,我们也是需要对提交的数据做相关的校验的 Form 组件提供了表单验证的功能,只需要通过 rules 属性传入约定的验证规则,并将 Form-Item 的 prop 属性设置为需校验的字段名即可 校验的页面效果 前端数据…...

pytorch的用法
...

Qt 设置窗口背景
窗口背景无非两种:背景色、背景图片。Qt中窗口背景如何设置? 一、QPalette设置背景 二、实现paintEvent,使用QPainter来绘制背景 三、使用QSS来设置背景 关于QSS的使用不想多说,一般我不用QSS设置窗口背景,也不建议…...

大模型是什么?泰迪大模型能够解决企业哪些痛点?
什么是大模型? 大模型是指模型具有庞大的参数规模和复杂程度的机器学习模型。在深度学习领域,大模型通常是指具有数百万到数十亿参数的神经网络模型。这些模型需要大量的计算资源和存储空间来训练和存储,并且往往需要进行分布式计算和特殊…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

理解 MCP 工作流:使用 Ollama 和 LangChain 构建本地 MCP 客户端
🌟 什么是 MCP? 模型控制协议 (MCP) 是一种创新的协议,旨在无缝连接 AI 模型与应用程序。 MCP 是一个开源协议,它标准化了我们的 LLM 应用程序连接所需工具和数据源并与之协作的方式。 可以把它想象成你的 AI 模型 和想要使用它…...

cf2117E
原题链接:https://codeforces.com/contest/2117/problem/E 题目背景: 给定两个数组a,b,可以执行多次以下操作:选择 i (1 < i < n - 1),并设置 或,也可以在执行上述操作前执行一次删除任意 和 。求…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

【2025年】解决Burpsuite抓不到https包的问题
环境:windows11 burpsuite:2025.5 在抓取https网站时,burpsuite抓取不到https数据包,只显示: 解决该问题只需如下三个步骤: 1、浏览器中访问 http://burp 2、下载 CA certificate 证书 3、在设置--隐私与安全--…...

零基础设计模式——行为型模式 - 责任链模式
第四部分:行为型模式 - 责任链模式 (Chain of Responsibility Pattern) 欢迎来到行为型模式的学习!行为型模式关注对象之间的职责分配、算法封装和对象间的交互。我们将学习的第一个行为型模式是责任链模式。 核心思想:使多个对象都有机会处…...

什么?连接服务器也能可视化显示界面?:基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11?环境准备实战步骤1️⃣ 服务器端配置(CentOS)2️⃣ 客户端配置(MobaXterm)3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
MySQL用户和授权
开放MySQL白名单 可以通过iptables-save命令确认对应客户端ip是否可以访问MySQL服务: test: # iptables-save | grep 3306 -A mp_srv_whitelist -s 172.16.14.102/32 -p tcp -m tcp --dport 3306 -j ACCEPT -A mp_srv_whitelist -s 172.16.4.16/32 -p tcp -m tcp -…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...
