【每日一题Day310】LC1654到家的最少跳跃次数 | BFS
到家的最少跳跃次数【LC1654】
有一只跳蚤的家在数轴上的位置
x处。请你帮助它从位置0出发,到达它的家。跳蚤跳跃的规则如下:
- 它可以 往前 跳恰好
a个位置(即往右跳)。- 它可以 往后 跳恰好
b个位置(即往左跳)。- 它不能 连续 往后跳
2次。- 它不能跳到任何
forbidden数组中的位置。跳蚤可以往前跳 超过 它的家的位置,但是它 不能跳到负整数 的位置。
给你一个整数数组
forbidden,其中forbidden[i]是跳蚤不能跳到的位置,同时给你整数a,b和x,请你返回跳蚤到家的最少跳跃次数。如果没有恰好到达x的可行方案,请你返回-1。
-
思路:最短路问题,BFS
-
**BFS:**寻找最少跳跃次数,所以可以使用最短路径Dijkstra 算法,通过BFS实现,队列元素需要存储当前跳跃次数以及当前位置;
-
**记录状态:**由于跳跃时连续向前次数不受限制,但是不能连续向后跳两次,因此跳跃时还需要记录前一跳跃的状态为向后还是向前;
- 如果前一状态为向前,那么本次可以向前也可以向后
- 如果前一状态为向后,那么本次只可以向前
-
判断是否可以访问:
- 首先判断最远右边界,由于向前跳跃次数不受限制,避免超时,需要寻找最远右边界【重点】
- 当前位置不在
forbidden数组中 - 之前没有访问过该状态【位置+方向】
-
寻找最远右边界:
-
如果 a ≥ b a\ge b a≥b,那么最远右边界为 x + b x+b x+b,在大于 x + b x+b x+b的位置不可能到达 x x x。
-
如果 a < b a\lt b a<b,那么可以先向前跳再向后跳逐步接近目标位置 x x x,最远右边界为 m a x ( f + a + b , x ) max(f+a+b, x) max(f+a+b,x),其中 f f f为 m a x ( f o r b i d d e n ) max(forbidden) max(forbidden)证明略。
感性认知:对于任何一条路径,若它包含了超过 m a x ( f + a + b , x ) max(f+a+b, x) max(f+a+b,x)的点,总能通过变换找到所有点都在 m a x ( f + a + b , x ) max(f+a+b, x) max(f+a+b,x)内的路径,且这条路径与原路径跳跃次数相同,对于该问题,这两条路径是等价的,所以只需考虑 m a x ( f + a + b , x ) max(f+a+b,x) max(f+a+b,x)内的路径即可
-
-
-
实现
class Solution {public int minimumJumps(int[] forbidden, int a, int b, int x) {Set<Integer> vis = new HashSet<>();Deque<int[]> pq = new LinkedList<>();// 跳跃次数、当前位置、连续向后跳次数int max = 0; for (int f : forbidden){vis.add(f);max = Math.max(max, f);} if (a > b){max = x + b;}else{max = Math.max(max + a + b, x);}boolean[][] flag = new boolean[max + 1][2];// 向前 向后一次flag[0][0] = true;pq.addLast(new int[]{0, 0, 0});while (!pq.isEmpty()){int[] node = pq.pollFirst();if (node[1] == x) return node[0]; // 向前int forward = node[1] + a;if (forward <= max && !vis.contains(forward) && !flag[forward][0]){flag[forward][0] = true;pq.addLast(new int[]{node[0] + 1, forward, 0});}// 向后int backward = node[1] - b;if (node[2] != 1 && backward >= 0 && !vis.contains(backward) && !flag[backward][1]){flag[backward][1] = true;pq.addLast(new int[]{node[0] + 1, backward, 1});}}return -1;} }
相关文章:

【每日一题Day310】LC1654到家的最少跳跃次数 | BFS
到家的最少跳跃次数【LC1654】 有一只跳蚤的家在数轴上的位置 x 处。请你帮助它从位置 0 出发,到达它的家。 跳蚤跳跃的规则如下: 它可以 往前 跳恰好 a 个位置(即往右跳)。它可以 往后 跳恰好 b 个位置(即往左跳&…...
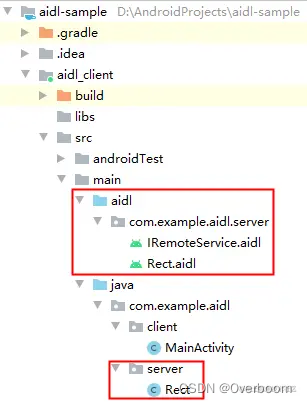
[Android AIDL] --- AIDL原理简析
上一篇文章已经讲述了如何在Android studio中搭建基于aidl的cs模型框架,只是用起来了,这次对aidl及cs端如何调用的原理进行简单分析 1 创建AIDL文件 AIDL 文件可以分为两类。 一类是用来定义接口方法,声明要暴露哪些接口给客户端调用&#…...

企业的固定资产管理怎么操作
一家拥有多台大型设备的工厂,这些设备需要定期进行保养和维护,以确保其正常运转。而企业内部员工由于专业知识和技能的不同,需要分工协作才能更好地完成各项工作任务。因此,在设备资产管理方面,如何实现高效、便捷、透…...

Rust 进阶学习
Rust 进阶学习 文章目录 Rust 进阶学习所有权作用域移动和克隆涉及函数的所有权机制涉及参数的所有权涉及返回值的所有权 引用和租借可变引用 枚举类枚举成员的属性枚举匹配 结构体结构体方法结构体关联函数 错误处理不可恢复错误可恢复错误 Rust代码组织管理Module默认的Modul…...
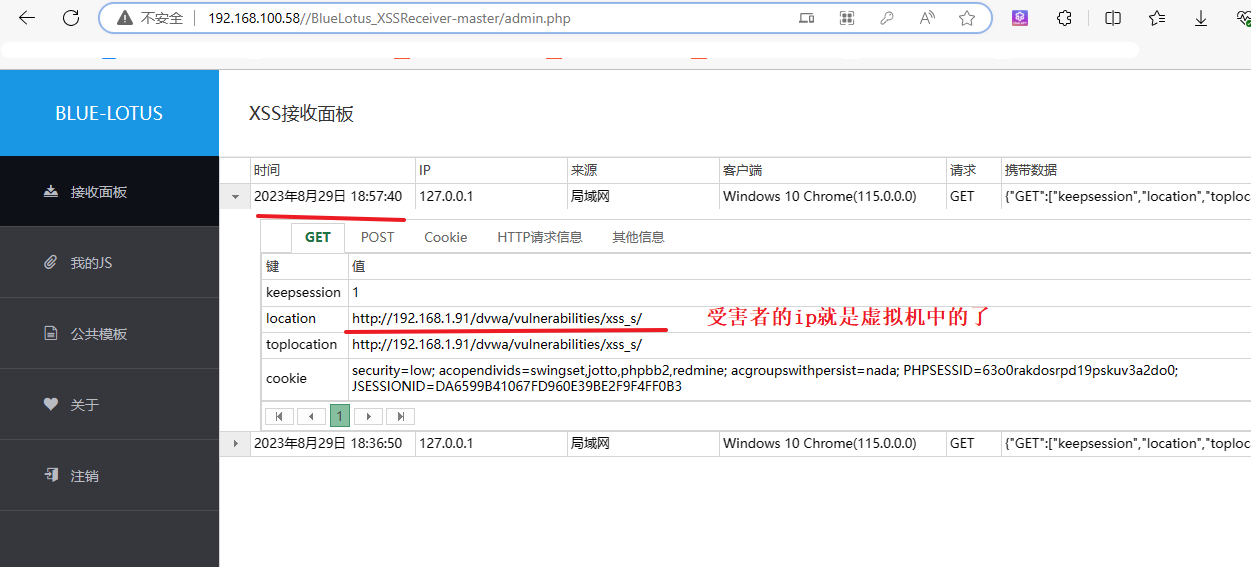
保护网站安全:学习蓝莲花的安装和使用,复现跨站脚本攻击漏洞及XSS接收平台
这篇文章旨在用于网络安全学习,请勿进行任何非法行为,否则后果自负。 环境准备 一、XSS基础 1、反射型XSS 攻击介绍 原理 攻击者通过向目标网站提交包含恶意脚本的请求,然后将该恶意脚本注入到响应页面中,使其他用户在查看…...
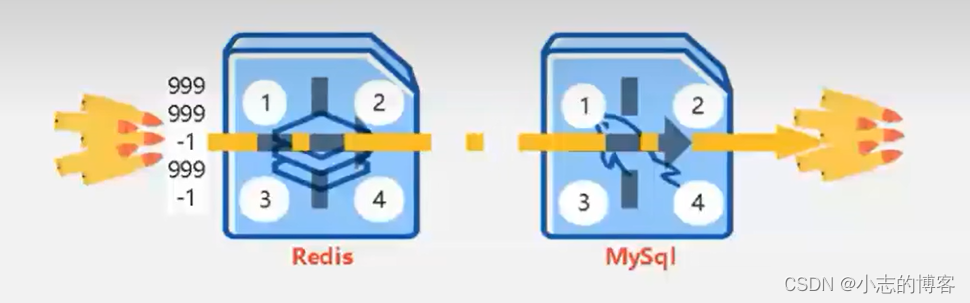
Redis——如何解决redis穿透、雪崩、击穿问题
目录 一、查询商品信息的常规代码示例二、缓存击穿2.1、缓存击穿的理解2.2、缓存击穿的解决方案2.3、解决缓存击穿的代码示例 三、缓存雪崩3.1、缓存雪崩的理解3.2、缓存雪崩的解决方案3.2.1、缓存集中过期的情况3.2.2、缓存服务器宕机的情况3.2.3、缓存服务器断电的情况 3.3、…...
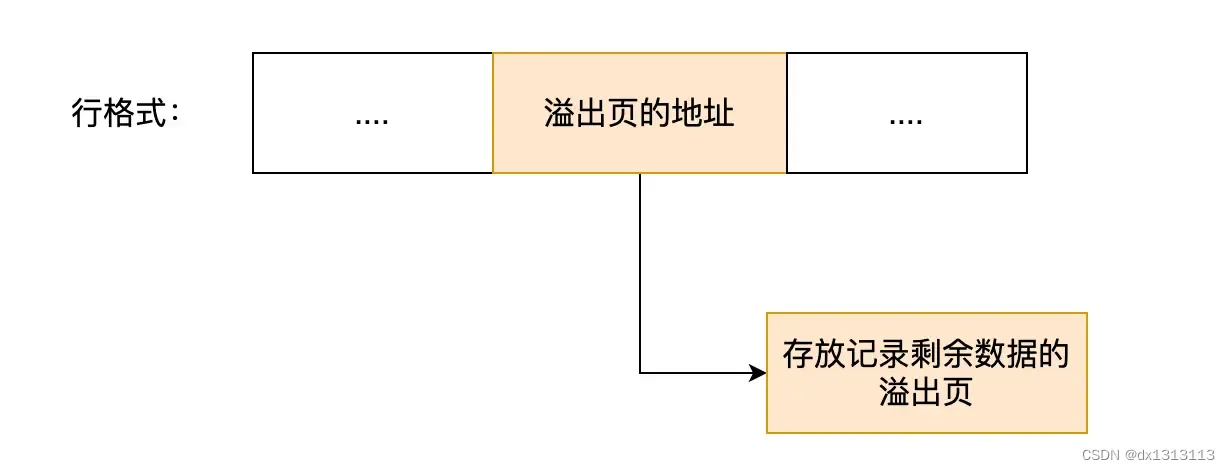
MySQL一行记录是如何存储的?
目录 MySQL的数据存放在哪个文件? 表空间文件的结构是怎么样的? 1、行(row) 2、页(page) 3、区(extent) 4、段(segment) InnoDB 行格式有哪些…...

[element-ui] el-tree全部展开与收回
shrinkTreeNode () {// 改变一个全局变量this.treeStatus !this.treeStatus;// 改变每个节点的状态this.changeTreeNodeStatus(this.$refs.attrList.store.root); },// 改变节点的状态 changeTreeNodeStatus (node) {node.expanded this.treeStatus;for (let i 0; i < no…...

git 统计(命令)
查询某人某个时刻提交了多少代码 added 添加代码 removed 删除代码 total 总代码 git log --author刘俊秦 --since2023-08-01 00:00:00 --until2023-08-23 23:00:00 --prettytformat: --numstat | awk { add $1; subs $2; loc $1 - $2 } END { printf "added lines: %s…...
)
斐波那契1(矩阵快速幂加速递推,斐波那契前n项平方和)
链接:登录—专业IT笔试面试备考平台_牛客网 来源:牛客网 Keven 特别喜欢斐波那契数列,已知 fib11fib_11fib11,fib21fib_21fib21,对于 n>3n>3n>3,fibnfibn−2fibn−1fib_{n}fib_{n-2}fib_{n…...

minikube mac 启动
系统信息如下 最开始使用的minikube是1.22.0版本,按照如下命令启动: minikube start --memory7851 --cpus4 --image-mirror-countrycn遇到了下面一些问题: 1、拉取coredns:v1.8.0镜像失败 Error response from daemon: manifest for regis…...
从零开始学习 Java:简单易懂的入门指南之查找算法及排序算法(二十)
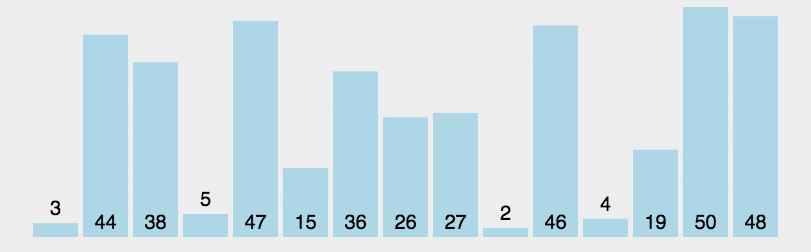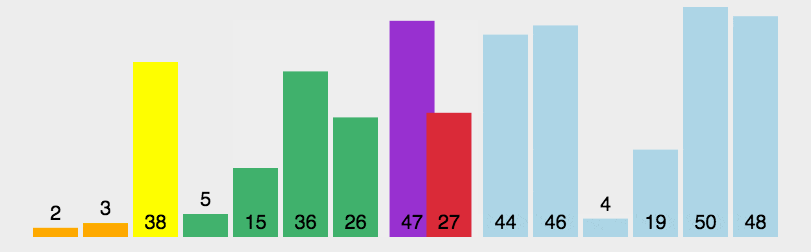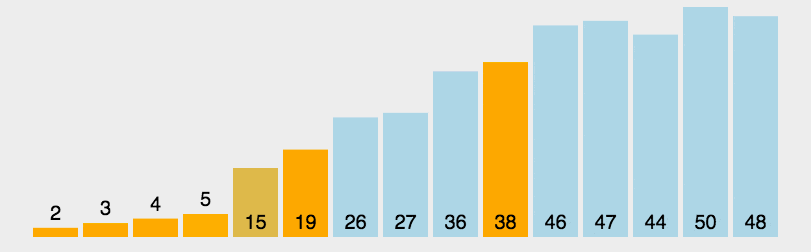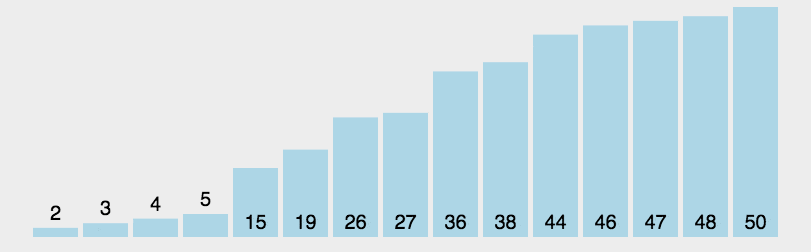
查找算法及排序算法 常见的七种查找算法:1. 基本查找2. 二分查找3. 插值查找4. 斐波那契查找5. 分块查找6. 哈希查找7. 树表查找 四种排序算法:1. 冒泡排序1.1 算法步骤1.2 动图演示1.3 代码示例 2. 选择排序2.1 算法步骤2.2 动图演示 3. 插入排序3.1 算…...

非煤矿山风险监测预警算法 yolov8
非煤矿山风险监测预警算法通过yolov8网络模型深度学习算法框架,非煤矿山风险监测预警算法在煤矿关键地点安装摄像机等设备利用智能化视频识别技术,能够实时分析人员出入井口的情况,人数变化并检测作业状态。YOLO的结构非常简单,就…...
Ansible学习笔记(一)
1.什么是Ansible 官方网站:https://docs.ansible.com/ansible/latest/installation_guide/intro_installation.html Ansible是一个配置管理和配置工具,类似于Chef,Puppet或Salt。这是一款很简单也很容易入门的部署工具,它使用SS…...

2024毕业设计选题指南【附选题大全】
title: 毕业设计选题指南 - 如何选择合适的毕业设计题目 date: 2023-08-29 categories: 毕业设计 tags: 选题指南, 毕业设计, 毕业论文, 毕业项目 - 如何选择合适的毕业设计题目 当我们站在大学生活的十字路口,毕业设计便成了我们面临的一项重要使命。这不仅是对我们…...
Error: PostCSS plugin autoprefixer requires PostCSS 8 问题解决办法
报错:Error: PostCSS plugin autoprefixer requires PostCSS 8 原因:autoprefixer版本过高 解决方案: 降低autoprefixer版本 执行:npm i postcss-loader autoprefixer8.0.0...
)
pymongo通过oplog获取数据(mongodb)
使用 MongoDB 的 oplog(操作日志)进行数据同步是高级的用法,主要用于复制和故障恢复。需要确保源 MongoDB 实例是副本集的一部分,因为只有副本集才会维护 oplog。 以下是简化的步骤,描述如何使用 oplog 进行数据同步&…...
MySQL数据备份与恢复
备份的主要目的: 备份的主要目的是:灾难恢复,备份还可以测试应用、回滚数据修改、查询历史数据、审计等。 日志: MySQL 的日志默认保存位置为: /usr/local/mysql/data##配置文件 vim /etc/my.cnf [mysqld] ##错误日志…...
基于ssm+vue汽车售票网站源码和论文
基于ssmvue汽车售票网站源码和论文088 开发工具:idea 数据库mysql5.7 数据库链接工具:navcat,小海豚等 技术:ssm 摘 要 互联网发展至今,无论是其理论还是技术都已经成熟,而且它广泛参与在社会中的方方面面。它让…...
)
【List】List集合有序测试案例:ArrayList,LinkedList,Vector(123)
List是有序、可重复的容器。 有序: List中每个元素都有索引标记。可以根据元素的索引标记(在List中的位置)访问 元素,从而精确控制这些元素。 可重复: List允许加入重复的元素。更确切地讲,List通常允许满足 e1.equals(e2) 的元素…...

【kafka】Golang实现分布式Masscan任务调度系统
要求: 输出两个程序,一个命令行程序(命令行参数用flag)和一个服务端程序。 命令行程序支持通过命令行参数配置下发IP或IP段、端口、扫描带宽,然后将消息推送到kafka里面。 服务端程序: 从kafka消费者接收…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

.Net框架,除了EF还有很多很多......
文章目录 1. 引言2. Dapper2.1 概述与设计原理2.2 核心功能与代码示例基本查询多映射查询存储过程调用 2.3 性能优化原理2.4 适用场景 3. NHibernate3.1 概述与架构设计3.2 映射配置示例Fluent映射XML映射 3.3 查询示例HQL查询Criteria APILINQ提供程序 3.4 高级特性3.5 适用场…...

Oracle查询表空间大小
1 查询数据库中所有的表空间以及表空间所占空间的大小 SELECTtablespace_name,sum( bytes ) / 1024 / 1024 FROMdba_data_files GROUP BYtablespace_name; 2 Oracle查询表空间大小及每个表所占空间的大小 SELECTtablespace_name,file_id,file_name,round( bytes / ( 1024 …...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

Web 架构之 CDN 加速原理与落地实践
文章目录 一、思维导图二、正文内容(一)CDN 基础概念1. 定义2. 组成部分 (二)CDN 加速原理1. 请求路由2. 内容缓存3. 内容更新 (三)CDN 落地实践1. 选择 CDN 服务商2. 配置 CDN3. 集成到 Web 架构 …...

五子棋测试用例
一.项目背景 1.1 项目简介 传统棋类文化的推广 五子棋是一种古老的棋类游戏,有着深厚的文化底蕴。通过将五子棋制作成网页游戏,可以让更多的人了解和接触到这一传统棋类文化。无论是国内还是国外的玩家,都可以通过网页五子棋感受到东方棋类…...
