机器学习策略——优化深度学习系统
正交化(Orthogonalization)
老式电视机,有很多旋钮可以用来调整图像的各种性质,对于这些旧式电视,可能有一个旋钮用来调图像垂直方向的高度,另外有一个旋钮用来调图像宽度,也许还有一个旋钮用来调梯形角度,还有一个旋钮用来调整图像左右偏移,还有一个旋钮用来调图像旋转角度之类的。
在这种情况下,正交化指的是电视设计师设计这样的旋钮,使得每个旋钮都只调整一个性质,这样调整电视图像就容易得多,就可以把图像调到正中。
设计出正交化的控制装置,最理想的情况是和你实际想控制的性质一致,这样你调整参数时就容易得多。
确保四件事情。
1.首先,你通常必须确保至少系统在训练集上得到的结果不错,所以训练集上的表现必须通过某种评估,达到能接受的程度。
2.在训练集上表现不错之后,你就希望系统也能在开发集上有好的表现。
3.然后你希望系统在测试集上也有好的表现。
4.在最后,你希望系统在测试集上系统的成本函数在实际使用中表现令人满意。
如果你的算法在成本函数上不能很好地拟合训练集,你想要一个旋钮,、或者一组特定的旋钮,这样你可以用来确保你的可以调整你的算法,让它很好地拟合训练集,所以你用来调试的旋钮可能是训练更大的网络,或者可以切换到更好的优化算法,比如Adam优化算法,等等。
如果你的算法在训练集上做得很好,但开发集不行,然后你有一组正则化的旋钮可以调节,尝试让系统满足第二个条件。增大训练集可以是另一个可用的旋钮,它可以帮助你的学习算法更好地归纳开发集的规律。
如果它不符合第三个标准呢?如果系统在开发集上做的很好,但测试集上做得不好呢?如果是这样,那么你需要调的旋钮,可能是更大的开发集。因为如果它在开发集上做的不错,但测试集不行这可能意味着你对开发集过拟合了,你需要往回退一步,使用更大的开发集。
最后,如果它在测试集上做得很好,但无法给你的用户提供良好的体验,这意味着你需要回去,改变开发集或成本函数。因为如果根据某个成本函数,系统在测试集上做的很好,但它无法反映你的算法在现实世界中的表现,这意味着要么你的开发集分布设置不正确,要么你的成本函数测量的指标不对。
在机器学习中,如果你可以观察你的系统,如果它在训练集上做的不好、在开发集上做的不好、它在测试集上做的不好,或者它在测试集上做的不错,但在现实世界中不好,必须弄清楚到底是什么地方出问题了,然后我们刚好有对应的旋钮,或者一组对应的旋钮,刚好可以解决那个限制了机器学习系统性能的问题。
单一数字评估指标 (Single Number Evaluation Metric)
应用机器学习是一个非常经验性的过程,我们通常有一个想法,编程序,跑实验,看看效果如何,然后使用这些实验结果来改善你的想法,然后继续走这个循环,不断改进你的算法。
比如说对于一个的猫分类器,之前你搭建了某个分类器 A,通过改变超参数,还有改变训练集等手段,你现在训练出来了一个新的分类器 B,所以评估你的分类器的一个合理方式是观察它的查准率(precision)和查全率(recall)。
查准率的定义是在你的分类器标记为猫的例子中,有多少真的是猫。所以如果分类器 A 有95%的查准率,这意味着你的分类器说图片有猫的时候,有95%的机会真的是猫。
查全率就是,对于所有真猫的图片,你的分类器正确识别出了多少百分比。实际为猫的图片中,有多少被系统识别出来?如果分类器 A 查全率是90%,这意味着对于所有的图像,比如说你的开发集都是真的猫图,分类器 A 准确地分辨出了其中的90%。
事实证明,查准率和查全率之间往往需要折衷,两个指标都要顾及到。你希望得到的效果是,当你的分类器说某个东西是猫的时候,有很大的机会它真的是一只猫,但对于所有是猫的图片,你也希望系统能够将大部分分类为猫,所以用查准率和查全率来评估分类器是比较合理的。
但使用查准率和查全率作为评估指标的时候,如果你尝试了很多不同想法,很多不同的超参数,你希望能够快速试验十几个分类器,快速选出 “最好的” 那个,如果使用查准率和查全率两个评估指标,分类器 A 在查全率上表现更好,分类器 B 在查准率上表现更好,你就无法判断哪个分类器更好,就很难去快速地二中选一或者十中选一,所以实际应用中并不推荐同时使用查准率和查全率来选择一个分类器。你只需要找到一个新的评估指标,能够结合查准率和查全率。
在机器学习文献中,结合查准率和查全率的标准方法是所谓的 F 1 F1 F1 分数。非正式的,你可以认为这是查准率 P 和查全率 R 的平均值。正式来看, F 1 F1 F1 分数的定义是这个公式: 2 1 P + 1 R \frac{2}{\frac{1}{P} + \frac{1}{R}} P1+R12
在数学中,这个函数叫做查准率 P 和查全率 R 的调和平均数。
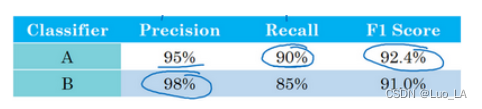
在上图这个例子中,你可以马上看出,分类器 A 的 F 1 F1 F1 分数更高。你可以快速选出分类器 A ,淘汰分类器 B 。
满足和优化指标 (Satisficing and Optimizing Metrics)
要把你顾及到的所有事情组合成单实数评估指标有时并不容易,在这些情况里,设立满足和优化指标是很重要的。
当选择一个分类器,能够最大限度提高准确度,但必须满足运行时间要求,例如对图像进行分类所需的时间必须小于等于100毫秒。所以在这种情况下,我们就说准确度是一个优化指标,因为你想要准确度最大化,你想做的尽可能准确,但是运行时间就是我们所说的满足指标,意思是它必须足够好,它只需要小于100毫秒,达到之后,你不在乎这指标有多好,或者至少你不会那么在乎。所以这是一个相当合理的权衡方式,或者说将准确度和运行时间结合起来的方式。实际情况可能是,只要运行时间少于100毫秒,你的用户就不会在乎运行时间是100毫秒还是50毫秒,甚至更快。
通过定义优化和满足指标,就可以给你提供一个明确的方式,去选择“最好的”分类器。
更一般地说,如果你要考虑 N 个指标,有时候选择其中一个指标做为优化指标是合理的。所以你想尽量优化那个指标,然后剩下 N − 1 个指标都是满足指标,意味着只要它们达到一定阈值,例如运行时间快于100毫秒,你不在乎它超过那个门槛之后的表现,但它们必须达到这个门槛。
训练/开发/测试集划分 (Train/Dev/Test Distribution)
设立训练集,开发集和测试集的方式大大影响了你或者你的团队在建立机器学习应用方面取得进展的速度。
开发(dev)集也叫做开发集(development set),有时称为保留交叉验证集(hold out cross validation set)。机器学习中的工作流程是,你尝试很多思路,用训练集训练不同的模型,然后使用开发集来评估不同的思路,然后选择一个,然后不断迭代去改善开发集的性能,直到最后你可以得到一个令你满意的成本,然后你再用测试集去评估。
在划分开发集和测试集时,应该将所有的数据随机洗牌,放入开发集和测试集,使得两部分数据是来自同一分布的。
开发集和测试集的大小 (Size of Dev and Test Sets)
你可能听说过一条经验法则,在机器学习中,把你取得的全部数据用70/30比例分成训练集和测试集。或者如果你必须设立训练集、开发集和测试集,你会这么分60%训练集,20%开发集,20%测试集。在机器学习的早期,这样分是相当合理的,特别是以前的数据集大小要小得多。
但在现代机器学习中,我们更习惯操作规模大得多的数据集,比如说你有1百万个训练样本,这样分可能更合理,98%作为训练集,1%开发集,1%测试集,我们用 D 和 T 缩写来表示开发集和测试集。因为如果你有1百万个样本,那么1%就是10,000个样本,这对于开发集和测试集来说可能已经够了。所以在现代深度学习时代,有时我们拥有大得多的数据集,所以使用小于20%的比例或者小于30%比例的数据作为开发集和测试集也是合理的。
什么时候改变开发和测试集评估指标 (When to change dev/test sets and metrics)
前面已经讲过如何设置开发集和评估指标,就像是把目标定在某个位置,让你的团队瞄准。但有时候在项目进行途中,你可能意识到,目标的位置放错了。这种情况下,你应该移动你的目标。
方针是,如果你在指标上表现很好,在当前开发集或者开发集和测试集分布中表现很好,但你的实际应用程序,你真正关注的地方表现不好,那么就需要修改指标或者你的开发测试集。
相关文章:

机器学习策略——优化深度学习系统
正交化(Orthogonalization) 老式电视机,有很多旋钮可以用来调整图像的各种性质,对于这些旧式电视,可能有一个旋钮用来调图像垂直方向的高度,另外有一个旋钮用来调图像宽度,也许还有一个旋钮用来…...

ES6中Proxy和Proxy实例
1.Proxy Proxy 这个词的原意是代理,用在这里表示由它来“代理”某些操作,可以译为“代理器” 使用方法 let p new Proxy(target, handler);其中,target 为被代理对象。handler 是一个对象,其声明了代理 target 的一些操作。p 是…...

UDP协议的重要知识点
UDP,即用户数据报协议(User Datagram Protocol),是一个简单的无连接的传输层协议。与TCP相比,UDP提供了更少的错误检查机制,并允许数据包在网络上更快地传输。在这篇博客中,我们将深入探讨UDP的…...
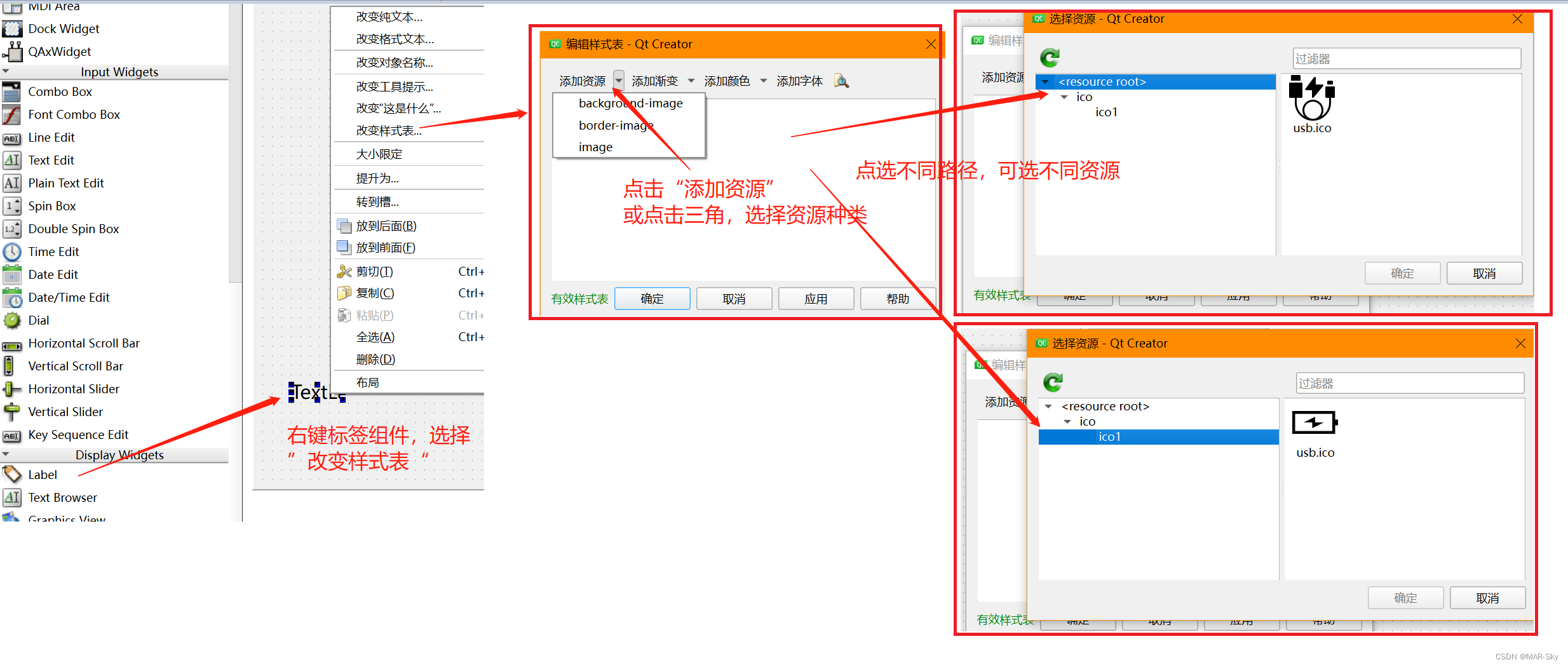
QT6为工程添加资源文件,并在ui界面引用
以添加图片资源为例 右键工程名字(不是最上面的名字),点击添加现有文件 这种方式虽然添加到了工程中,但不能在UI设计界面完成引用。主要原因可能是未把文件放入到项目资源文件中,以下面一种方式可以看出区别。 点击添…...

Python小知识 - 如何使用Python的Flask框架快速开发Web应用
如何使用Python的Flask框架快速开发Web应用 现在越来越多的人把Python作为自己的第一语言来学习,Python的简洁易学的语法以及丰富的第三方库让人们越来越喜欢上了这门语言。本文将介绍如何使用Python的Flask框架快速开发Web应用。 Flask是一个使用Python编写的轻量级…...
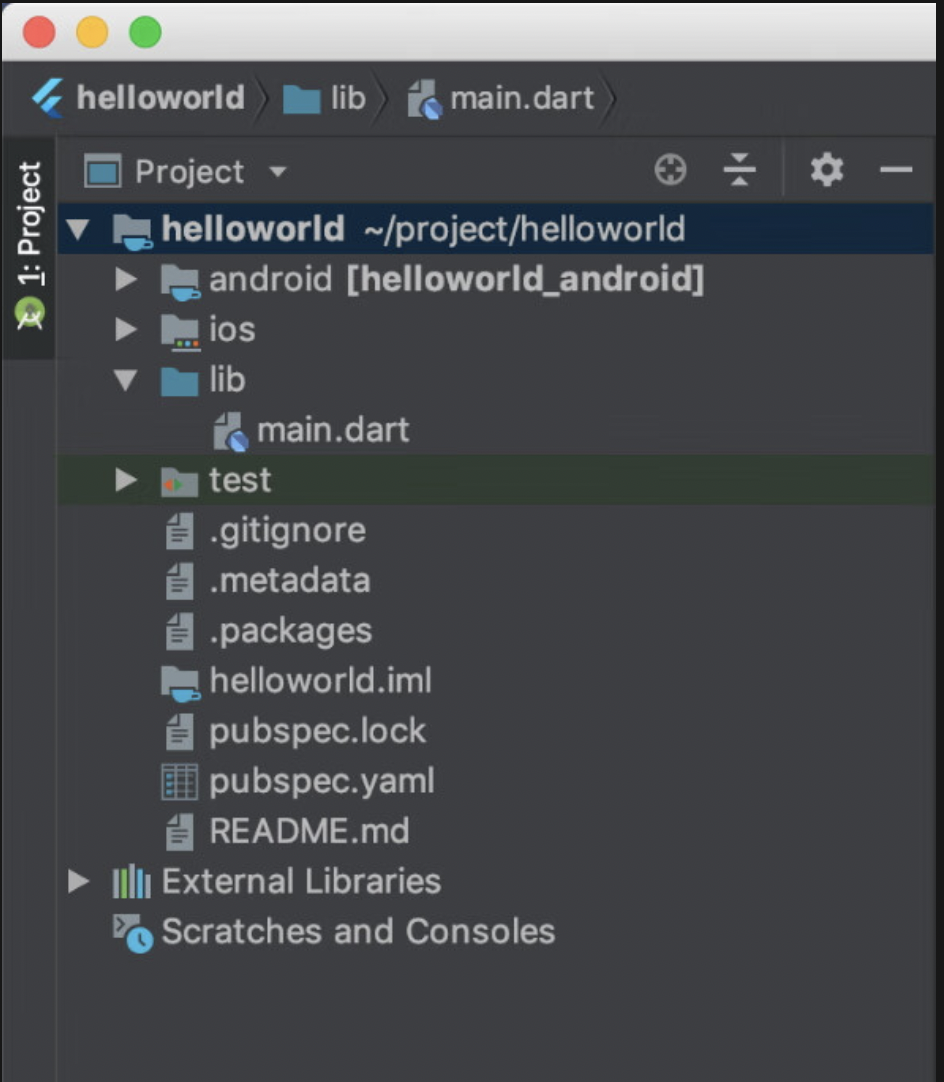
Flutter 项目结构文件
1、Flutter项目的文件结构 先helloworld项目,看看它都包含哪些组成部分。首先,来看一下项目的文件结构,如下图所示。 2、介绍上图的内容。 -litb/main.dart文件:整个应用的入口文件,其中的main函数是整个Flutter应…...
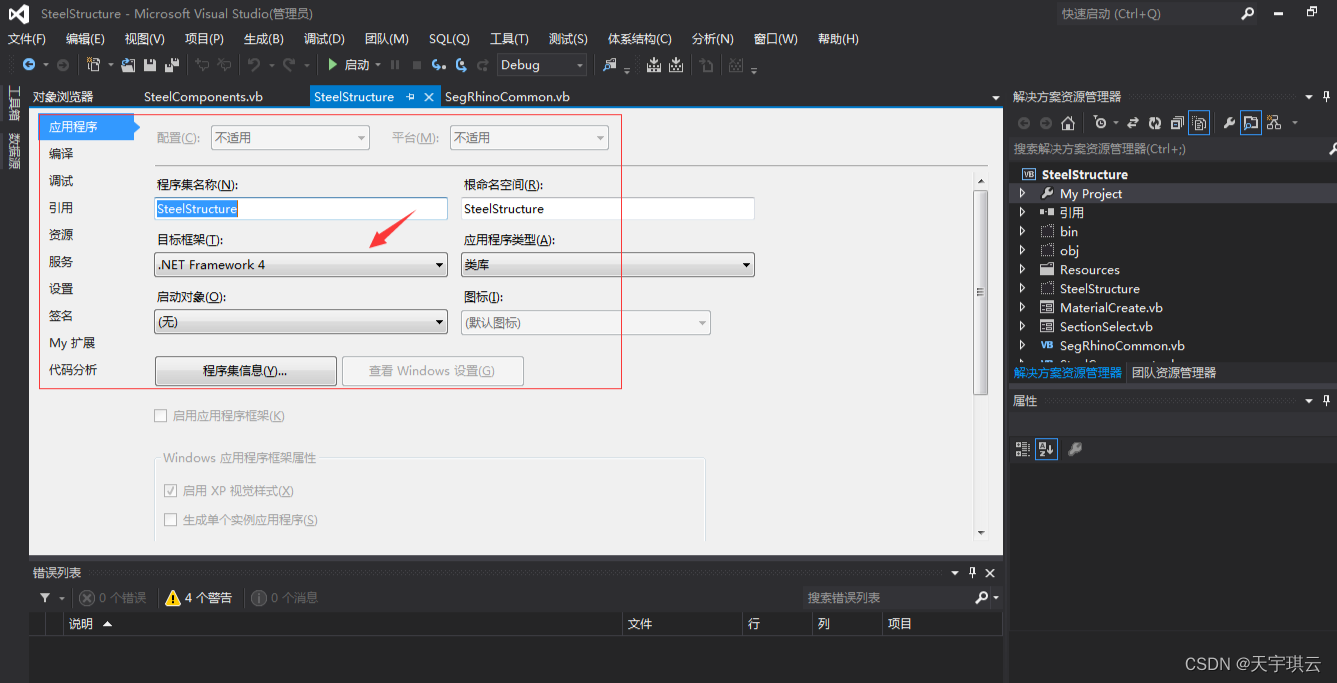
未找到System.Runtime.InteropServices.Marshal.GetTypeFromCLSID(System.Guid) 方法错误
记录此问题实际上是由于.netFrame框架配置太高引起的,一般常见于二次开发中,因为二次开发一般都是引用的com组件,在引用过程中后台代码调用了 Method not found: System.Type System.Runtime.InteropServices.Marshal.GetTypeFromCLSID(Syste…...
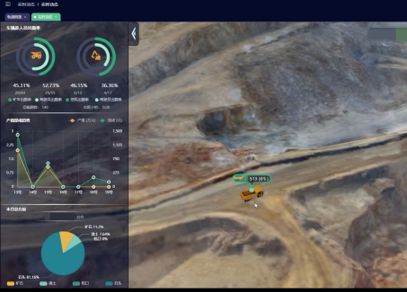
人员位置管理,点亮矿山安全之路
矿山作为一个高危行业,安全问题一直备受关注。人员定位置管理是现代矿山安全管理的重要一环,可以帮助企业更好地实现对人员的实时监控和管理。因此,矿山人员位置管理系统对于矿山安全生产和管理非常重要,可以帮助减少安全事故的发…...
node-red - 读写操作redis
node-red - 读写操作redis 一、前期准备二、node-red安装redis节点三、node-red操作使用redis节点3.1 redis-out节点 - 存储数据到redis3.2 redis-cmd节点 - 存储redis数据3.3 redis-in节点 - 查询redis数据 附录附录1:redis -out节点示例代码附录2:redi…...

【图像处理】模板匹配的学习笔记
OpenCV的模板匹配算法 cv.TM_CCOEFFcv.TM_CCOEFF_NORMEDcv.TM_CCORRcv.TM_CCORR_NORMEDcv.TM_SQDIFFcv.TM_SQDIFF_NORMED 匹配代码模板 image cv2.imread(r"scene.png", cv2.IMREAD_GRAYSCALE) template cv2.imread(r"element.png", cv2.IMREAD_GRAYSC…...

Ext JS之Ext Direct快速入门
Ext Direct是一个专有名词, Direct是直接的意思。 Ext Direct 是 Ext JS 框架中的一个功能模块,用于简化前端 JavaScript 应用程序与后端服务器之间的通信和数据交换。 Ext Direct 提供了一种直接的、透明的方式来调用服务器上的方法和处理服务器响应,而无需编写大量的手动…...
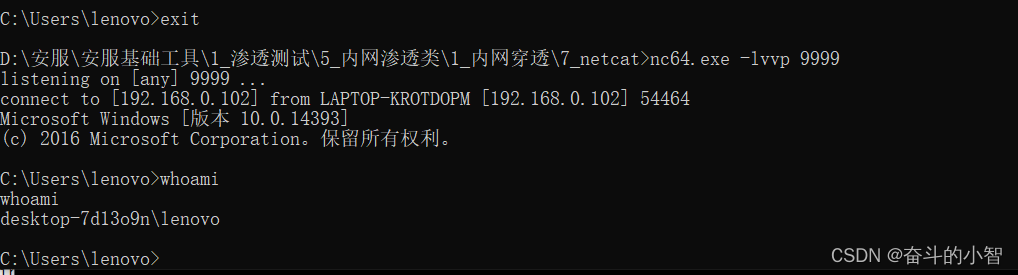
内网隧道技术学习
1. 隧道技术 在进行渗透测试以及攻防演练的时候,通常会存在各种边界设备、软硬件防火墙、IPS等设备来检测外部连接情况,这些设备如果发现异常,就会对通信进行阻断。 那么隧道技术就是一种绕过端口屏蔽的通信方式,在实际情况中防…...

【前端】CSS3新特性
目录 一、前言二、伪元素选择器1、选择器2、注意事项3、代码示例 三、伪元素清除浮动1、第一种伪元素清除浮动2、第二种伪元素清除浮动 四、CSS3盒子模型1、box-sizing:content-box2、box-sizing:border-box 五、CSS3图片模糊处理1、图片变模糊①、CSS3滤…...

Spring之HandlerInterceptor和RequestBodyAdvice
一个请求在Spring中处理流程是有多种方式拦截处理的,而且,请求是可以拆分为进入和响应2个操作的,进入我们通常会对请求参数做处理,而响应我们通常会对响应参数做处理,Spring提供了多种方式给开发者。 一、HandlerInte…...

transition、transform 区别和应用
先说应用 1.动画循环,复杂的动画用animation。在遇到很复杂的动画那就用animation。因为animation可以定义关键帧。那你就可以控制每一帧的动画效果。 2.简单的动画,事件触发用transition。当页面中的动画是自己执行的那么我们考虑用animation…...
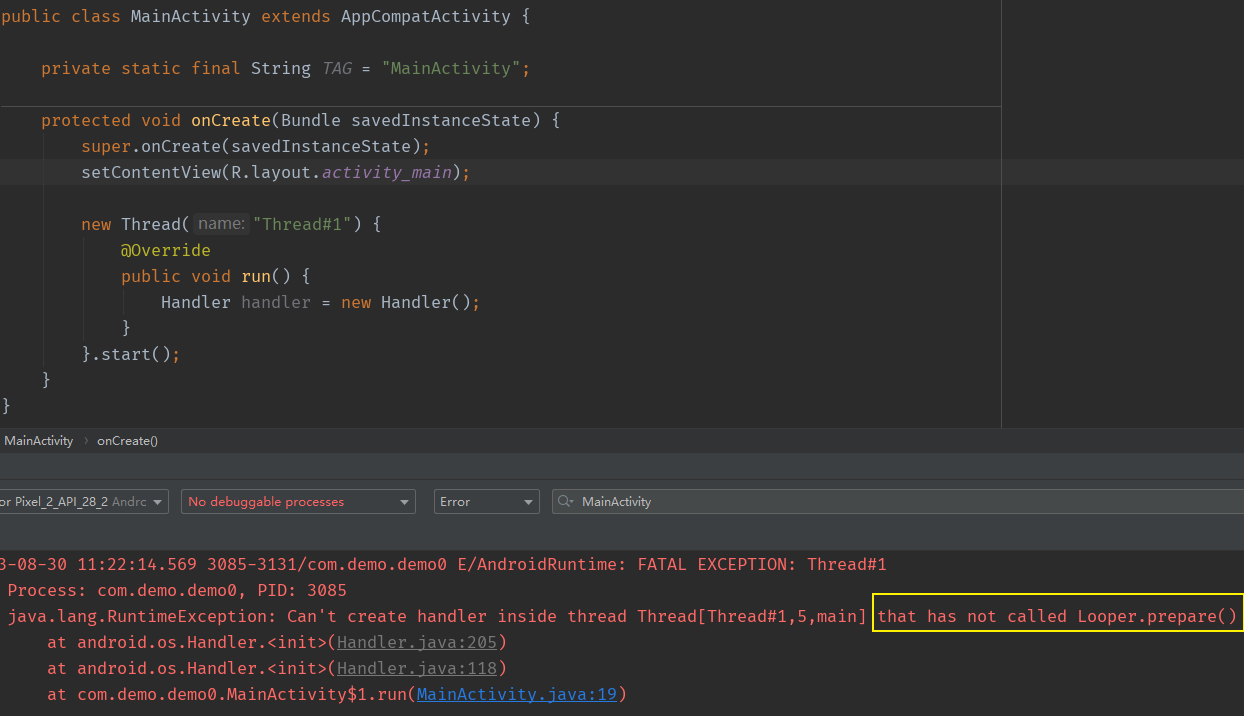
Android中级——消息机制
消息机制 概念ThreadLocalMessageQueueLooperHandlerrunOnUiThread() 概念 MessageQueue:采用单链表的方法存储消息列表Looper:查询MessageQueue是否有新消息,有则处理,无则等待ThreadLocal:用于Handler获取当前线程的…...

【kubernetes】使用KubeSphere devops部署我的微服务系统
KubeSphere Devops 入门使用KubeSphere的Devops功能部署"我的微服务系统" (内容学习于尚硅谷云原生课程) kubesphere devops官方文档: https://v3-1.docs.kubesphere.io/zh/docs/devops-user-guide/how-to-use/create-a-pipeline-u…...

【哈士奇赠书活动 - 37期】- 〖深入浅出SSD:固态存储核心技术、原理与实战 第2版〗
文章目录 ⭐️ 赠书 - 《深入浅出SSD:固态存储核心技术、原理与实战 第2版》⭐️ 内容简介⭐️ 作者简介⭐️ 编辑推荐⭐️ 赠书活动 → 获奖名单 ⭐️ 赠书 - 《深入浅出SSD:固态存储核心技术、原理与实战 第2版》 ⭐️ 内容简介 本书从基础认知、核心技…...

25.CSS自定义形状按钮与悬停效果
效果 源码 <!DOCTYPE html> <html lang="en"> <head><meta charset="UTF-8"><title>CSS Custom Shape Button</title><link rel="stylesheet" href="style.css"> </head> <body&…...

两条速度相差1350倍的sql语句
一起来学习研究下,看看是什么导致的这么大差别: SQL1: select * from RESOURCES where RES_STATUS 1 and PLATFORM_FLAG1 and RES_ID in (select RES_ID from DOWNLOADRECORDSwhere DOWNLOADRECORDS_TIME > DATE_SUB(now(),INTERVAL 7 DAY) grou…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

反向工程与模型迁移:打造未来商品详情API的可持续创新体系
在电商行业蓬勃发展的当下,商品详情API作为连接电商平台与开发者、商家及用户的关键纽带,其重要性日益凸显。传统商品详情API主要聚焦于商品基本信息(如名称、价格、库存等)的获取与展示,已难以满足市场对个性化、智能…...

Java如何权衡是使用无序的数组还是有序的数组
在 Java 中,选择有序数组还是无序数组取决于具体场景的性能需求与操作特点。以下是关键权衡因素及决策指南: ⚖️ 核心权衡维度 维度有序数组无序数组查询性能二分查找 O(log n) ✅线性扫描 O(n) ❌插入/删除需移位维护顺序 O(n) ❌直接操作尾部 O(1) ✅内存开销与无序数组相…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

linux 错误码总结
1,错误码的概念与作用 在Linux系统中,错误码是系统调用或库函数在执行失败时返回的特定数值,用于指示具体的错误类型。这些错误码通过全局变量errno来存储和传递,errno由操作系统维护,保存最近一次发生的错误信息。值得注意的是,errno的值在每次系统调用或函数调用失败时…...

如何将联系人从 iPhone 转移到 Android
从 iPhone 换到 Android 手机时,你可能需要保留重要的数据,例如通讯录。好在,将通讯录从 iPhone 转移到 Android 手机非常简单,你可以从本文中学习 6 种可靠的方法,确保随时保持连接,不错过任何信息。 第 1…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

短视频矩阵系统文案创作功能开发实践,定制化开发
在短视频行业迅猛发展的当下,企业和个人创作者为了扩大影响力、提升传播效果,纷纷采用短视频矩阵运营策略,同时管理多个平台、多个账号的内容发布。然而,频繁的文案创作需求让运营者疲于应对,如何高效产出高质量文案成…...
