C语言每日一练------(Day3)
本专栏为c语言练习专栏,适合刚刚学完c语言的初学者。本专栏每天会不定时更新,通过每天练习,进一步对c语言的重难点知识进行更深入的学习。
今天练习题的关键字: 尼科彻斯定理 等差数列

💓博主csdn个人主页:小小unicorn
⏩专栏分类:C语言天天练
🚚代码仓库:小小unicorn的代码仓库🚚
🌹🌹🌹关注我带你学习编程知识
Day1
- 题目一:
- 题目描述:
- 解题思路:
- 思路一:
- 代码实现:
- 思路二:
- 思路三:
- 代码实现:
- 结果情况:
- 题目二:
- 题目描述:
- 解题思路:
- 代码实现:
- 结果情况:
- 总结:
题目一:
题目描述:
验证尼科彻斯定理…即:任何一个整数m的立方都可以写成m个连续奇数之和。 题目来源
例如:
1^3=1
2^3=3+5
3^3=7+9+11
4^3=13+15+17+19
输入一个正整数m(m≤100),将m的立方写成m个连续奇数之和的形式输出。
数据范围:
1≤m≤100
进阶:时间复杂度: O(m) ,空间复杂度:O(1)
输入描述:
输入一个int整数
输出描述:
输出分解后的string

解题思路:
思路一:
写几组例子:
1^3=1 —>1
2^3=3+5 ----> 4
3^3=7+9+11 —> 9
4^3=13+15+17+19 —> 16
我们会发现一个规律:
n x n x n=n x n两边的n个奇数相加。
代码实现:
#include <stdio.h>int main()
{int n=0;scanf("%d",&n);int m1=n*(n-1);int m2=n*(n+1);for(int i=m1+1;i<m2-1;i+=2){printf("%d+",i);}printf("%d",m2-1);return 0;
}
思路二:
m的立方,也就是m个m^2 的和相加,m个m^2 可以理解为m个等差为2,首项为m^2-m+1的数列, 即:m2-m+1,m2-m+3, …m2+m-1 共m项
eg: m=6
m1=6x6-6+1 =31
m2=6x6-6+1 +2 =33
m3=6x6-6+1+2+2 =35
m4=6x6-6+1+2+2+2 =37
m5=6x6-6+1+2+2+2+2 =39
m6=6x6-6+1+2+2+2+2+2 = 41
6x6x6=36x6=(36+36+36+36+36+36)=(36-1)+(36+1)+(36-3)+(36+3)+(36-5)+(36+5)
#include <stdio.h>
#include <string.h>
int main(void)
{int m;scanf("%d",&m);int *arr;arr=(int*)malloc(sizeof(int)*m);//分配m个int字节空间for(int i=0;i<m;i++){if(i==0)arr[i]=m*m-m+1;// 数列首项a[0]elsearr[i]=arr[i-1]+2;//通项:a[n]=a[n-1]+2}for(int i=0;i<2*m-1;i++){if(i%2==0)printf("%d",arr[i/2]);//偶数项打印数列elseprintf("%c",'+');//奇数项打印“+”号,但是最后项不能打印‘+’号,所以i<2*m-1,而不是i<2*m}return 0;
}
思路三:
认真对题目分析,可以将题目转换为:
已知等差数列前n项和,求a0问题。
等差数列求和公式为:Sn=nxa0+1/2n(n-1)d.
本题的公差为2也就是d为2.
由此可输出前n项和。
代码实现:
#include<stdio.h>int main()
{int m;scanf("%d",&m);int sn=m*m*m;int a0=sn/m-m+1;printf("%d",a0);for(int i=1;i<m;i++){printf("+%d",a0+2*i);}printf("\n");return 0;
}
结果情况:

符合题目要求,问题得到解决。
题目二:
题目描述:
等差数列 2,5,8,11,14。。。。(从 2 开始的 3 为公差的等差数列)
输出求等差数列前n项和
数据范围: 1≤n≤1000
题目来源
输入描述:
输入一个正整数n。
输出描述:
输出一个相加后的整数。
解题思路:
有了第一题的经验。第二题更简单,直接带等差数列求和公式即可。
代码实现:
#include<stdio.h>
int main()
{int a1 = 2, d = 3, an = 0, n = 0, Sn = 0;while (scanf("%d", &n) == 1) {an = a1 + (n - 1) * d;Sn = (a1 + an) * n / 2;printf("%d", Sn);}
}结果情况:

符合题目要求,问题得到解决。
总结:
今天的两道编程练习题,会发现有一个共同点,那就是都用到了等差数列的相关知识,所以解决有的问题卡主了,我们可以尝试将它转化为一个数学问题,用数学知识解决它。
文章到这里就要告一段落了,有更好的想法或问题,欢迎评论区留言。
希望今天的练习能对您有所收获,咱们下期见!
相关文章:

C语言每日一练------(Day3)
本专栏为c语言练习专栏,适合刚刚学完c语言的初学者。本专栏每天会不定时更新,通过每天练习,进一步对c语言的重难点知识进行更深入的学习。 今天练习题的关键字: 尼科彻斯定理 等差数列 💓博主csdn个人主页:…...
14、监测数据采集物联网应用开发步骤(10)
监测数据采集物联网应用开发步骤(9.2) Modbus rtu协议开发 本章节在《监测数据采集物联网应用开发步骤(7)》基础上实现可参考《...开发步骤(7)》调试工具,本章节代码需要调用modbus_tk组件,阅读本章节前建议baidu熟悉modbus rtu协议内容 组件安装modb…...
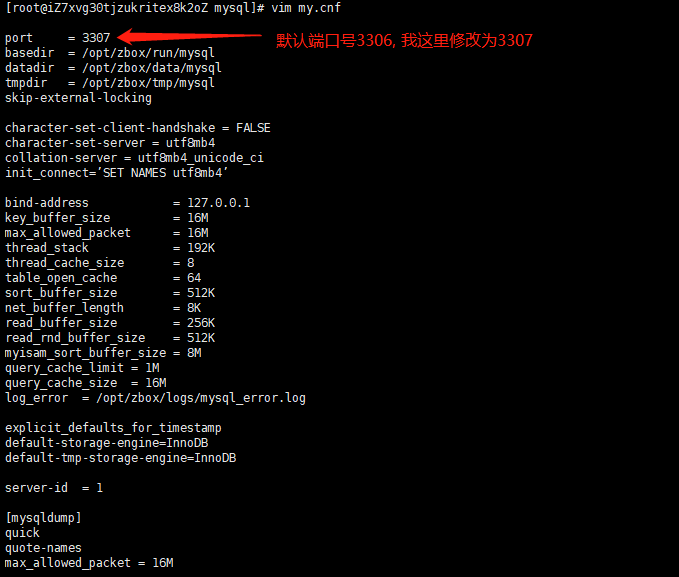
Linux禅道上修改Apache 和 MySQL 默认端口号
1. 修改Apache默认端口号 80 cd /opt/zbox/etc/apachevim httpd.conf :wq 保存 2. 修改MySQL默认端口号 3306 cd /opt/zbox/etc/mysql vim my.cnf :wq 保存 3. 重启服务 ./zbox restart...

操作教程|通过1Panel开源Linux面板快速安装DataEase
DataEase开源数据可视化分析工具(dataease.io)的在线安装是通过在服务器命令行执行Linux命令来进行的。但是在实际的安装部署过程中,很多数据分析师或者业务人员经常会因为不熟悉Linux操作系统及命令行操作方式,在安装DataEase的过…...
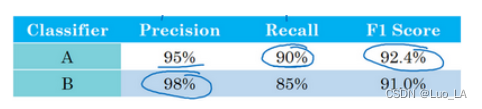
机器学习策略——优化深度学习系统
正交化(Orthogonalization) 老式电视机,有很多旋钮可以用来调整图像的各种性质,对于这些旧式电视,可能有一个旋钮用来调图像垂直方向的高度,另外有一个旋钮用来调图像宽度,也许还有一个旋钮用来…...

ES6中Proxy和Proxy实例
1.Proxy Proxy 这个词的原意是代理,用在这里表示由它来“代理”某些操作,可以译为“代理器” 使用方法 let p new Proxy(target, handler);其中,target 为被代理对象。handler 是一个对象,其声明了代理 target 的一些操作。p 是…...

UDP协议的重要知识点
UDP,即用户数据报协议(User Datagram Protocol),是一个简单的无连接的传输层协议。与TCP相比,UDP提供了更少的错误检查机制,并允许数据包在网络上更快地传输。在这篇博客中,我们将深入探讨UDP的…...
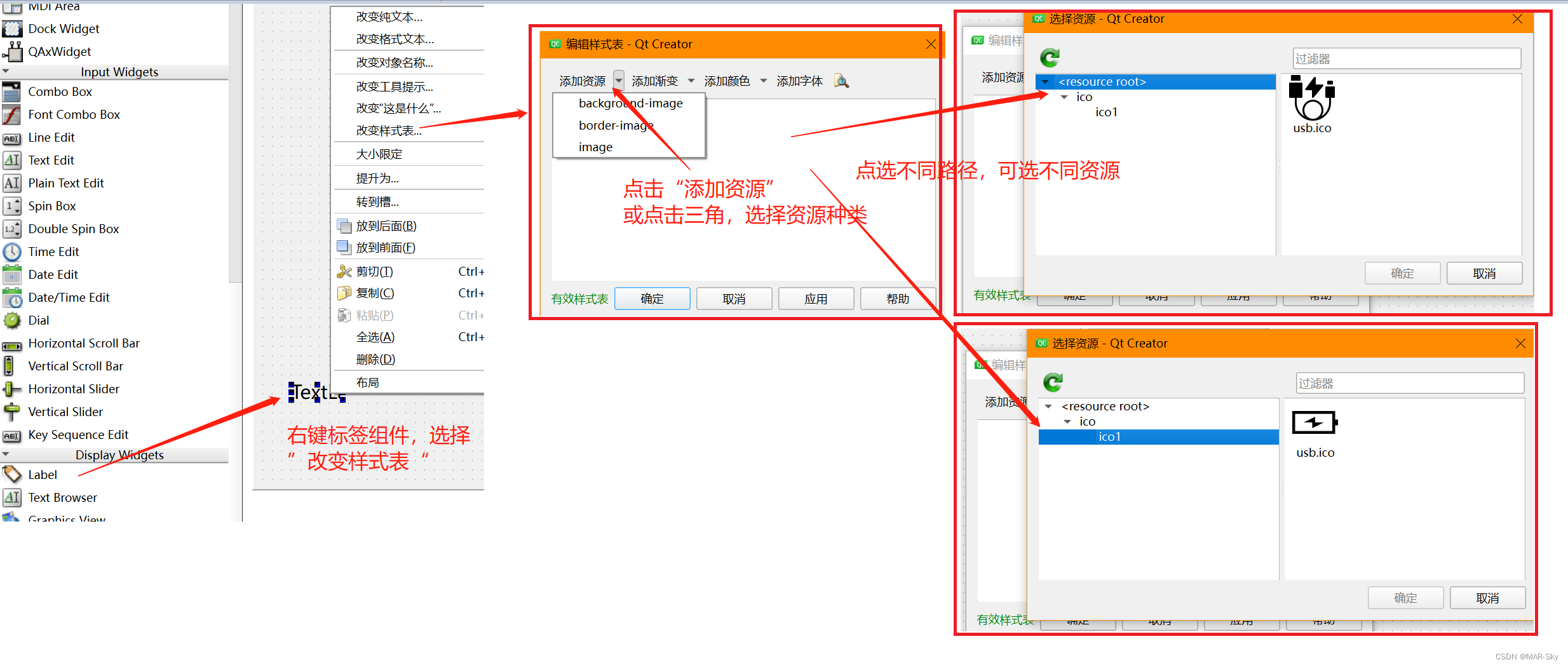
QT6为工程添加资源文件,并在ui界面引用
以添加图片资源为例 右键工程名字(不是最上面的名字),点击添加现有文件 这种方式虽然添加到了工程中,但不能在UI设计界面完成引用。主要原因可能是未把文件放入到项目资源文件中,以下面一种方式可以看出区别。 点击添…...

Python小知识 - 如何使用Python的Flask框架快速开发Web应用
如何使用Python的Flask框架快速开发Web应用 现在越来越多的人把Python作为自己的第一语言来学习,Python的简洁易学的语法以及丰富的第三方库让人们越来越喜欢上了这门语言。本文将介绍如何使用Python的Flask框架快速开发Web应用。 Flask是一个使用Python编写的轻量级…...
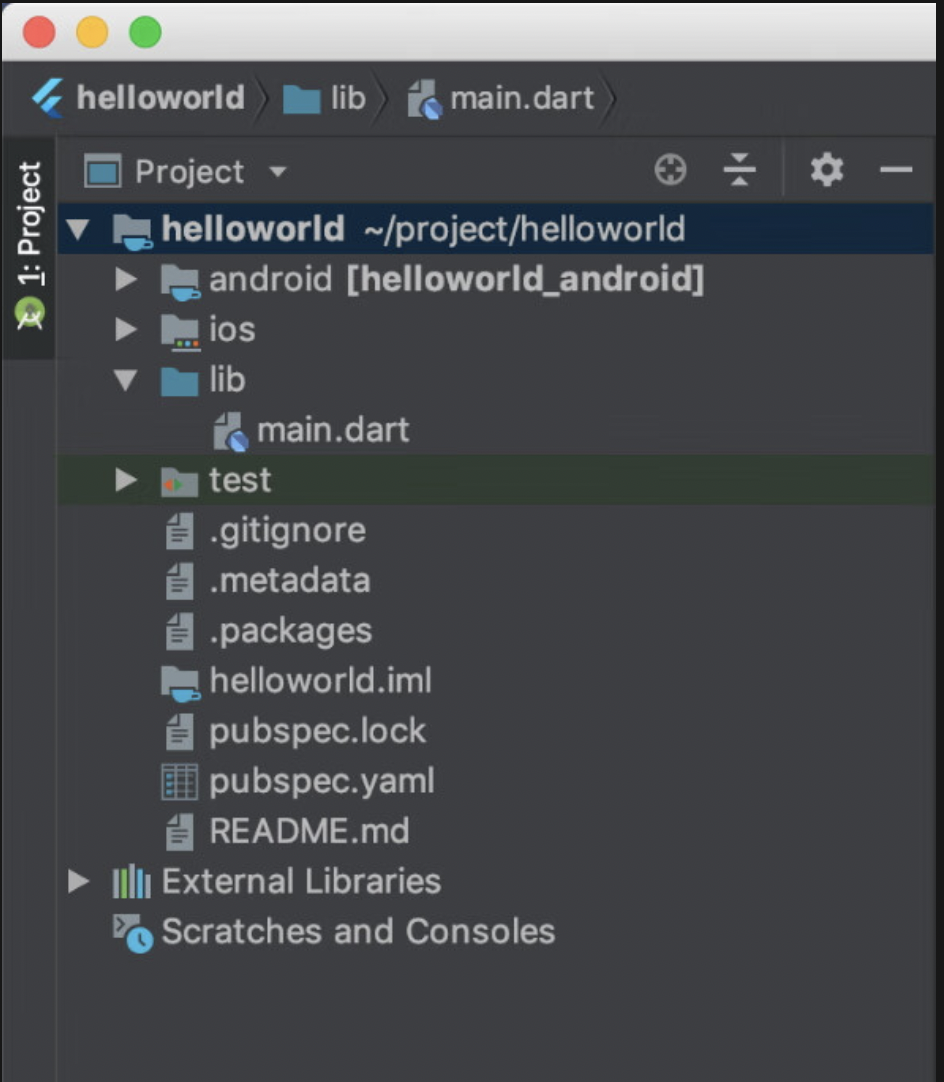
Flutter 项目结构文件
1、Flutter项目的文件结构 先helloworld项目,看看它都包含哪些组成部分。首先,来看一下项目的文件结构,如下图所示。 2、介绍上图的内容。 -litb/main.dart文件:整个应用的入口文件,其中的main函数是整个Flutter应…...
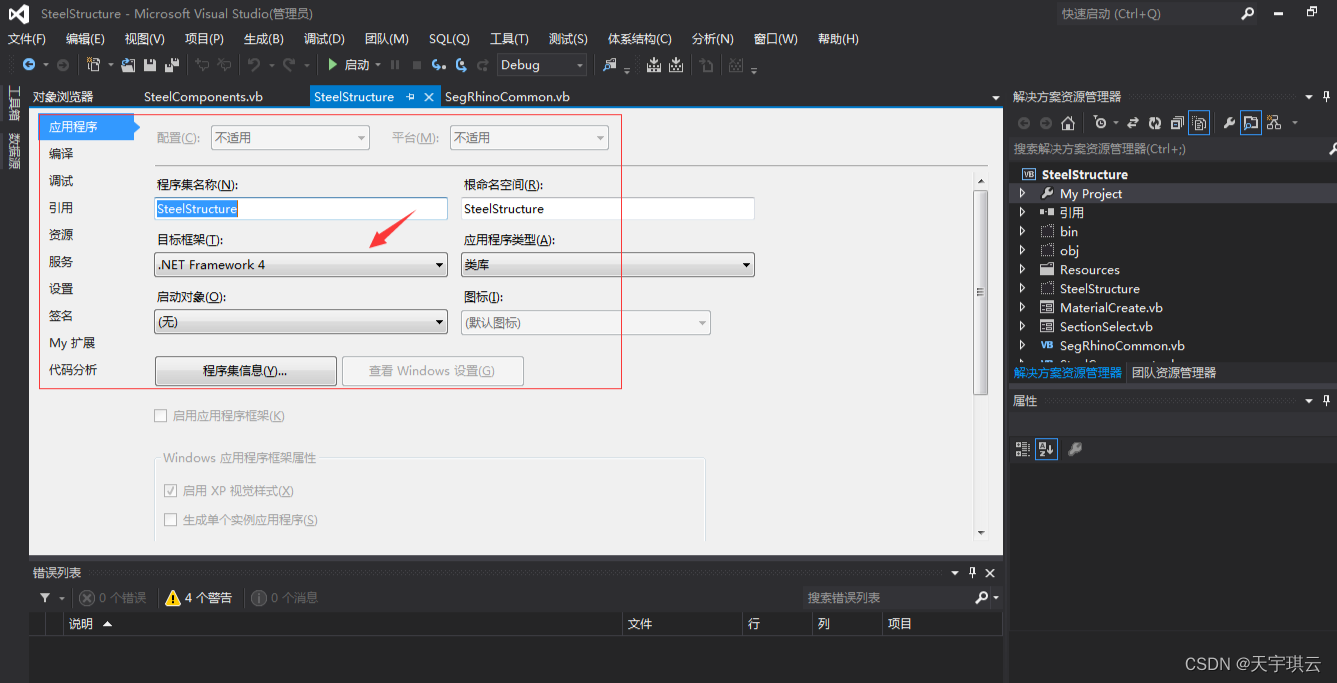
未找到System.Runtime.InteropServices.Marshal.GetTypeFromCLSID(System.Guid) 方法错误
记录此问题实际上是由于.netFrame框架配置太高引起的,一般常见于二次开发中,因为二次开发一般都是引用的com组件,在引用过程中后台代码调用了 Method not found: System.Type System.Runtime.InteropServices.Marshal.GetTypeFromCLSID(Syste…...
人员位置管理,点亮矿山安全之路
矿山作为一个高危行业,安全问题一直备受关注。人员定位置管理是现代矿山安全管理的重要一环,可以帮助企业更好地实现对人员的实时监控和管理。因此,矿山人员位置管理系统对于矿山安全生产和管理非常重要,可以帮助减少安全事故的发…...
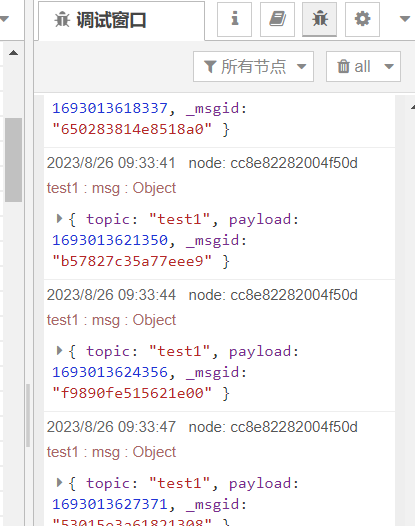
node-red - 读写操作redis
node-red - 读写操作redis 一、前期准备二、node-red安装redis节点三、node-red操作使用redis节点3.1 redis-out节点 - 存储数据到redis3.2 redis-cmd节点 - 存储redis数据3.3 redis-in节点 - 查询redis数据 附录附录1:redis -out节点示例代码附录2:redi…...

【图像处理】模板匹配的学习笔记
OpenCV的模板匹配算法 cv.TM_CCOEFFcv.TM_CCOEFF_NORMEDcv.TM_CCORRcv.TM_CCORR_NORMEDcv.TM_SQDIFFcv.TM_SQDIFF_NORMED 匹配代码模板 image cv2.imread(r"scene.png", cv2.IMREAD_GRAYSCALE) template cv2.imread(r"element.png", cv2.IMREAD_GRAYSC…...

Ext JS之Ext Direct快速入门
Ext Direct是一个专有名词, Direct是直接的意思。 Ext Direct 是 Ext JS 框架中的一个功能模块,用于简化前端 JavaScript 应用程序与后端服务器之间的通信和数据交换。 Ext Direct 提供了一种直接的、透明的方式来调用服务器上的方法和处理服务器响应,而无需编写大量的手动…...
内网隧道技术学习
1. 隧道技术 在进行渗透测试以及攻防演练的时候,通常会存在各种边界设备、软硬件防火墙、IPS等设备来检测外部连接情况,这些设备如果发现异常,就会对通信进行阻断。 那么隧道技术就是一种绕过端口屏蔽的通信方式,在实际情况中防…...

【前端】CSS3新特性
目录 一、前言二、伪元素选择器1、选择器2、注意事项3、代码示例 三、伪元素清除浮动1、第一种伪元素清除浮动2、第二种伪元素清除浮动 四、CSS3盒子模型1、box-sizing:content-box2、box-sizing:border-box 五、CSS3图片模糊处理1、图片变模糊①、CSS3滤…...

Spring之HandlerInterceptor和RequestBodyAdvice
一个请求在Spring中处理流程是有多种方式拦截处理的,而且,请求是可以拆分为进入和响应2个操作的,进入我们通常会对请求参数做处理,而响应我们通常会对响应参数做处理,Spring提供了多种方式给开发者。 一、HandlerInte…...

transition、transform 区别和应用
先说应用 1.动画循环,复杂的动画用animation。在遇到很复杂的动画那就用animation。因为animation可以定义关键帧。那你就可以控制每一帧的动画效果。 2.简单的动画,事件触发用transition。当页面中的动画是自己执行的那么我们考虑用animation…...
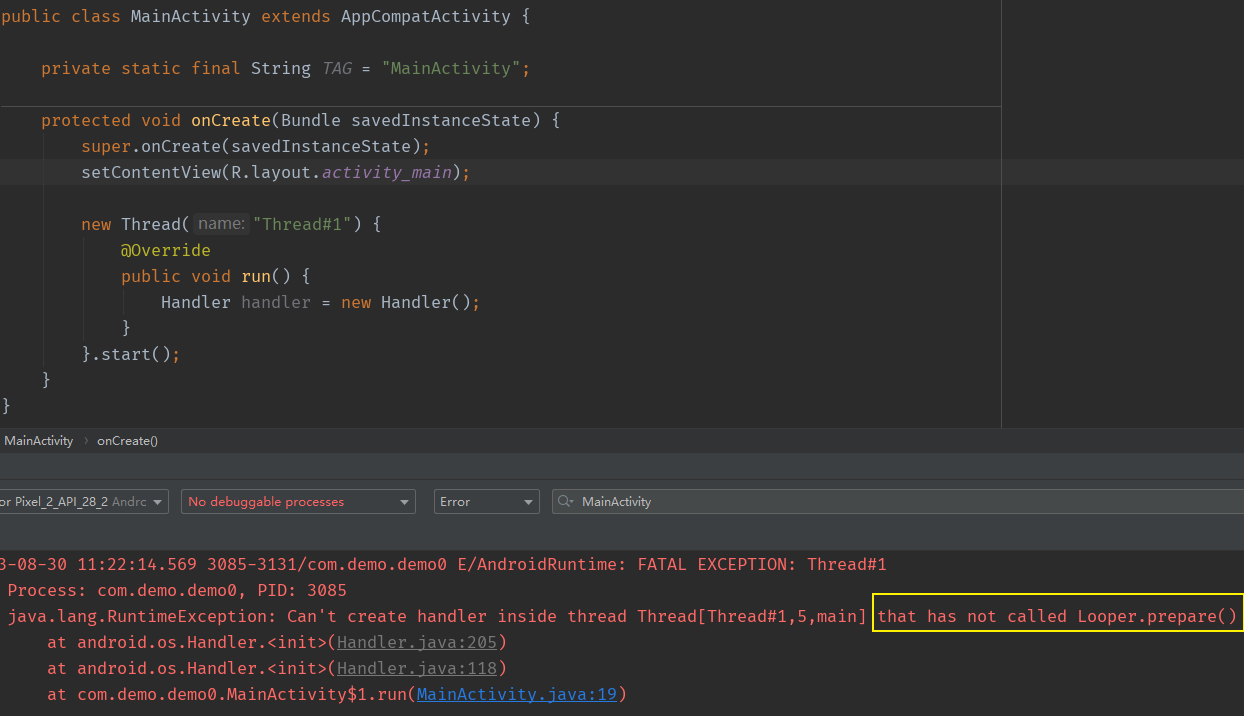
Android中级——消息机制
消息机制 概念ThreadLocalMessageQueueLooperHandlerrunOnUiThread() 概念 MessageQueue:采用单链表的方法存储消息列表Looper:查询MessageQueue是否有新消息,有则处理,无则等待ThreadLocal:用于Handler获取当前线程的…...

23-Oracle 23 ai 区块链表(Blockchain Table)
小伙伴有没有在金融强合规的领域中遇见,必须要保持数据不可变,管理员都无法修改和留痕的要求。比如医疗的电子病历中,影像检查检验结果不可篡改行的,药品追溯过程中数据只可插入无法删除的特性需求;登录日志、修改日志…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...
【机器视觉】单目测距——运动结构恢复
ps:图是随便找的,为了凑个封面 前言 在前面对光流法进行进一步改进,希望将2D光流推广至3D场景流时,发现2D转3D过程中存在尺度歧义问题,需要补全摄像头拍摄图像中缺失的深度信息,否则解空间不收敛…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

Maven 概述、安装、配置、仓库、私服详解
目录 1、Maven 概述 1.1 Maven 的定义 1.2 Maven 解决的问题 1.3 Maven 的核心特性与优势 2、Maven 安装 2.1 下载 Maven 2.2 安装配置 Maven 2.3 测试安装 2.4 修改 Maven 本地仓库的默认路径 3、Maven 配置 3.1 配置本地仓库 3.2 配置 JDK 3.3 IDEA 配置本地 Ma…...

Java求职者面试指南:计算机基础与源码原理深度解析
Java求职者面试指南:计算机基础与源码原理深度解析 第一轮提问:基础概念问题 1. 请解释什么是进程和线程的区别? 面试官:进程是程序的一次执行过程,是系统进行资源分配和调度的基本单位;而线程是进程中的…...

RSS 2025|从说明书学习复杂机器人操作任务:NUS邵林团队提出全新机器人装配技能学习框架Manual2Skill
视觉语言模型(Vision-Language Models, VLMs),为真实环境中的机器人操作任务提供了极具潜力的解决方案。 尽管 VLMs 取得了显著进展,机器人仍难以胜任复杂的长时程任务(如家具装配),主要受限于人…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...
