java实现二叉树(一文带你详细了解二叉树的)
🎇🎇🎇作者:
@小鱼不会骑车
🎆🎆🎆专栏:
《数据结构》
🎓🎓🎓个人简介:
一名专科大一在读的小比特,努力学习编程是我唯一的出路😎😎😎
二叉树
- 1. 树的定义
- 1.1 树的概念
- 1.1.1 概念
- 1.1.2 概念(重要)
- 1.2 树的表示形式
- 2. 二叉树
- 2.1 二叉树定义
- 2.2 二叉树的特点
- 2.2.1 二叉树的特点
- 2.2.2 二叉树的五种基本形态
- 2.3 两种特殊的二叉树
- 2.3.1 满二叉树
- 2.3.2 完全二叉树
- 2.4 二叉树的性质(由公式推导附加几道练习题)
- 2.5 二叉树的存储
- 2.6 二叉树的遍历
- 2.6.1 前序遍历
- 2.6.2 中序遍历
- 2.6.3 后续遍历
- 2.6.4 层序遍历
- 2.6.5 前中后遍历的练习题
- 2.7 二叉树的基本操作
- 2.7.1 获取二叉树结点个数
- 2.7.2 获取叶子节点个数
- 2.7.2.1 遍历思路
- 2.7.2.2 子问题思路
- 2.7.3 获取第K层结点的个数
- 2.7.3.1 遍历思路
- 2.7.3.2 子问题思路
- 2.7.4 获取二叉树的高度
- 2.7.5 检测value的元素是否存在
- 2.7.6 层序遍历
- 2.7.7 判断一颗树是不是完全二叉树
1. 树的定义
对于树,在我们现实生活中是非常常见的,大家可以看到,一个树由一个根部和很多树杈组成,就像这样:

那我们便可以根据这颗树联想到一种数据结构,就是树型结构,把它叫做树是因为它看
起来像一棵倒挂的树,也就是说它 是根朝上,而叶朝下的。
关于树的结构有很多种,但是我们现在主要学习的就是二叉树,对于AVL树,红黑树,B树,B+树,B*树……这些我们需要到高阶数据结构中才会了解到。
1.1 树的概念
1.1.1 概念
树(Tree):
-
树是n(n >= 0)个结点的有限集。n=0 时称为空树.
-
在任意一颗非空树中有且仅有一个特定的称为根(Root)的结点,并且根节点没有前驱结点.
-
当 n>1 时,其余节点可以分为m (m>0)个互不相交的有限集T1,T2……,Tn,其中每一个集合本身又是一棵树,并且称为根的子树(SubTree).

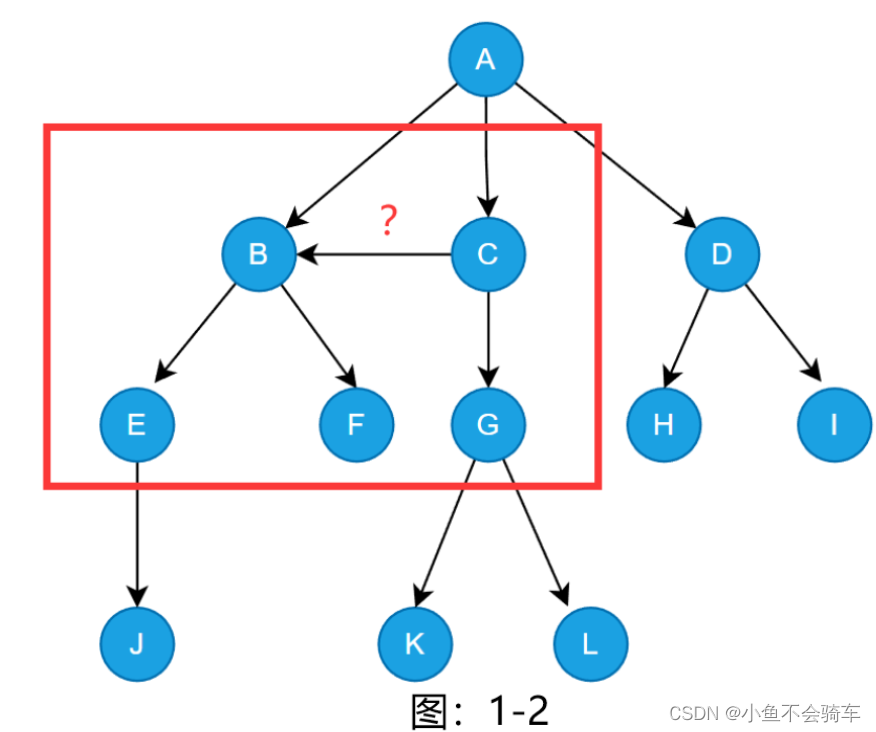
那我们再看看这是不是一颗树?
这种不是树,因为前面讲到过,子树之间不能有交集,切记!!!
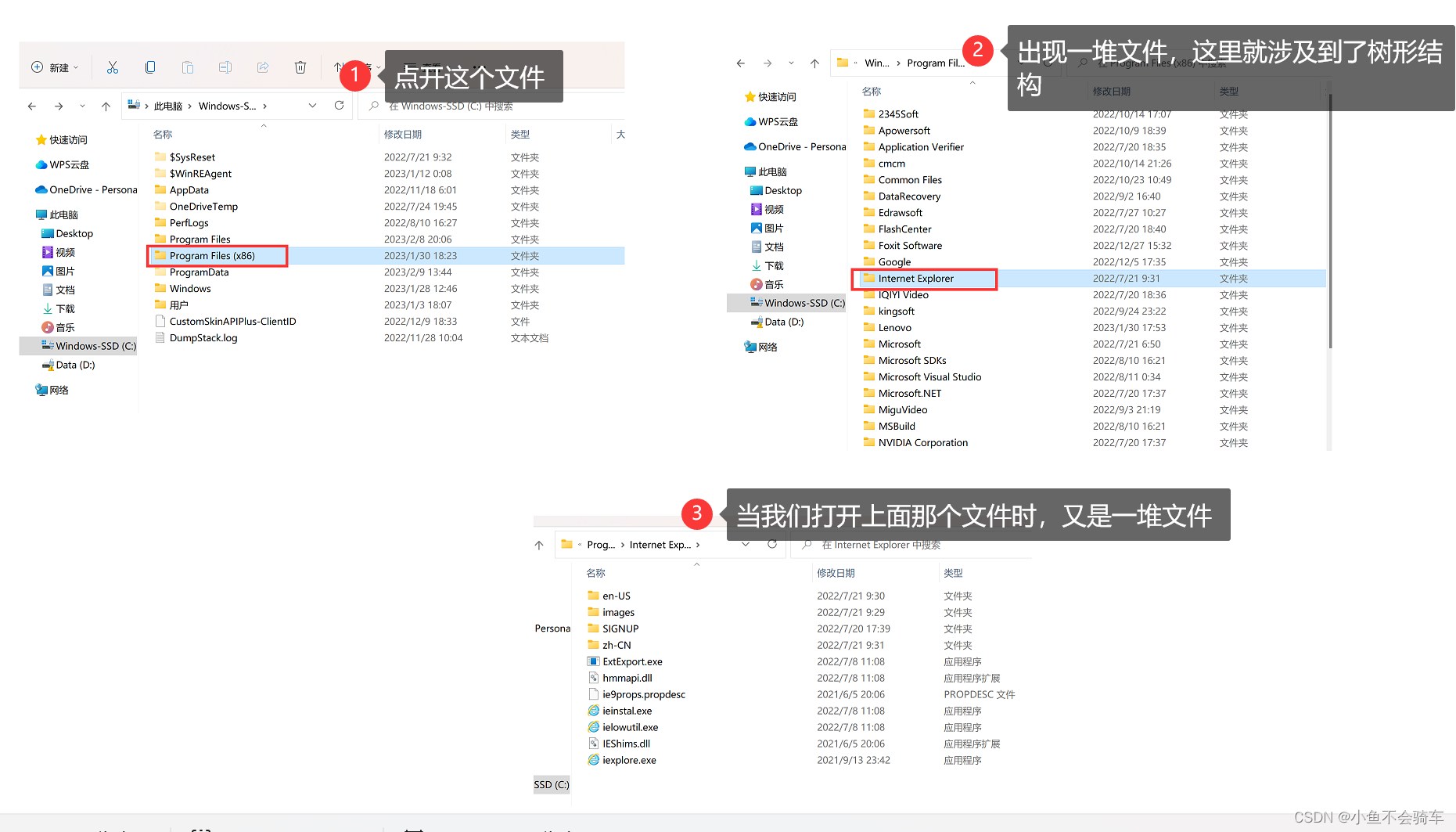
那我们在生活中都哪里用到了树形结构呢?
举例:
就像在文件夹中,我单开一个之后出现一堆文件,点开一个又是一堆文件,其实这里涉及到的结构就是树形结构。
1.1.2 概念(重要)
这里我们结合上述图片讲解(观看顺序:上文字,下图)
-
结点的度:一个结点含有子树的个数称为该结点的度; 如上图:A的度为3

-
树的度:一棵树中,所有结点度的最大值称为树的度; 如上图:树的度为3
-
叶子结点或终端结点:度为0的结点称为叶结点; 如上图:J,F,K,L,I节点为叶结点

- 双亲结点或父结点:若一个结点含有子结点,则这个结点称为其子结点的父结点; 如上图:A是B的父结点
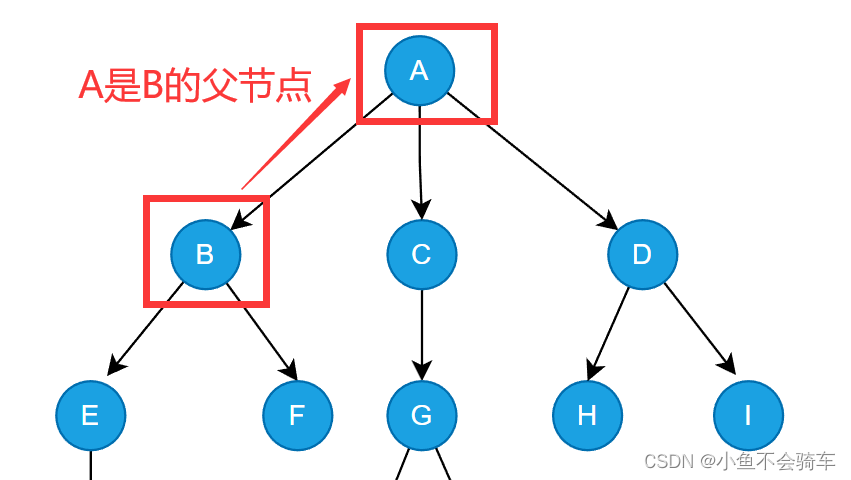
- 孩子结点或子结点:一个结点含有的子树的根结点称为该结点的子结点; 如上图:B是A的孩子结点

-
根结点:一棵树中,没有双亲结点的结点;如上图:A
-
结点的层次:从根开始定义起,根为第1层,根的子结点为第2层,以此类推

- 树的高度或深度:树中结点的最大层次; 如上图:树的高度为4
树的以下概念只需了解,在看书时只要知道是什么意思即可:
- 非终端结点或分支结点:度不为0的结点; 如上图:D、E、H、G…等节点为分支结点
- 兄弟结点:具有相同父结点的结点互称为兄弟结点; 如上图:B、C是兄弟结点
- 堂兄弟结点:双亲在同一层的结点互为堂兄弟;如上图:G、H、I互为堂兄弟结点
- 结点的祖先:从根到该结点所经分支上的所有结点;如上图:A是所有结点的祖先
- 子孙:以某结点为根的子树中任一结点都称为该结点的子孙。如上图:所有结点都是A的子孙
- 森林:由m(m>=0)棵互不相交的树组成的集合称为森林
另外强调两点重要的:
- n>0 时根节点时唯一的,不可能存在多个根节点,别和现实中的大叔混在一起,现实中的树有很多根须,那是真正的树,数据结构中的树只能有一个跟结点。
- m>0 时,子树的个数没有限制,但是他们一定是互不相交的,如上图1-2中的结构就不符合树的定义,因为他的子树相交了.
1.2 树的表示形式
树结构相对线性表就比较复杂了,要存储表示起来就比较麻烦了,实际中树有很多种表示方式,如:双亲表示法,孩子表示法、孩子双亲表示法、孩子兄弟表示法等等。我们这里就简单的了解其中最常用的孩子兄弟表示法。
class Node {int value; // 树中存储的数据Node firstChild; // 第一个孩子引用Node nextBrother; // 下一个兄弟引用
}

2. 二叉树
2.1 二叉树定义
我们做个小游戏:
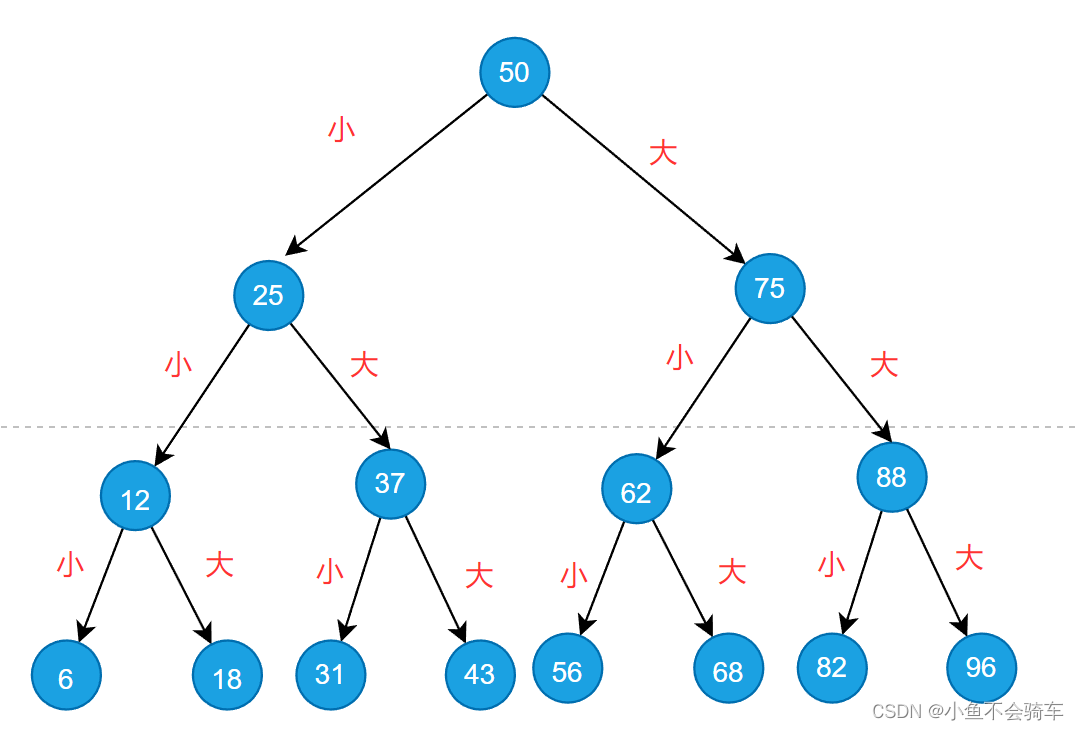
猜数字:我用计算机随机一个数字,数字范围为是1~100,每猜一个数字我就会告诉你猜 “大了” 或者猜“小了”,请大家想办法猜出这个数字,有一个前提条件是猜数字的次数不能超过7次。
这个游戏对于没有接触过数据结构或者算法的人来说,他们可能猜的方法是5,10,15这样一点点的增加进行猜测,这种效率其实是很差的。
其实正确的解法应该是折半查找算法,如下图,如果用的是该算法,就一定能在七次内猜出结果(下三层省略)。
我们通过下面的代码生成0~100的随机数
public static void main(String[] args) {Random random = new Random();Scanner scanner = new Scanner(System.in);int p = random.nextInt(100)+1;//(0包含,指定值不包含,所以+1,如果是0就变成1,如果是99就变成100)int size = 0;while (scanner.hasNextLine()) {int z = scanner.nextInt();if(z > p) {System.out.println("猜大了第"+(++size)+"次");}else if(z < p){System.out.println("猜小了第"+(++size)+"次");}else {System.out.println("第"+(++size)+"猜对了");break;}}}
下面开始测试:

如果我们用这种方式进行查找,效率会提高很多,我们可以想想,如果有100亿个数字,需要找到指定值,我们需要猜多少次?一百亿是10个0,我们按照2^10 = 1024 ,那么需要3个1024相乘再*10,我们向上取整,2 ^ 3 =8,2 ^ 4 = 16(16 > 10),我们取4,可以得出100亿约等于2 ^ 34,那么按照每次查找一半,只需呀log(2 ^ 34)次(默认以2为底)= 34,多么恐怖啊,100亿个数字中查找一个数只需呀34次!
并且不止是折半查找,对于这种某个阶段的结果都是两种形式的,比如开和关,0和1,真和假,上和下,对与错,正面与反面等,都适合用树状结构来建模,而这种树是一种很特殊的树状结构,叫做二叉树。
二叉树(Binary Tree)是 n ( n>=0 )个结点的有限集和,该集合或者为空集( 称为空二叉树 ),或者由一个根节点或两颗互不相交的,分别称为根节点的左子树和右子树的二叉树组成。
上图1-1的A结点有三个子树,所以不是二叉树。
2.2 二叉树的特点
2.2.1 二叉树的特点
- 每个结点最多有两棵子树,所以二叉树中不存在度大于2的结点。注意不是必须有子树,而是最多有。该节点没有子树或者只有一颗子树也都是可以的。
- 左子树和右子树是有顺序的,次序不能颠倒,就像我们穿鞋,如果左脚穿右鞋或者右脚穿左鞋那就会及其别扭和难受的。
- 即使树中某个结点只有一棵子树,也要区分它是左子树还是右子树,下图中,即使树1 和 树2 中存的值是一样的,但是由于结构不一样,所以他们不能称为完全相同的二叉树,就像你在班级里,你有一个同桌,那么你的同桌坐在你的左边和坐在你的右边是两种完全不一样的位序。即使人没有变,但是所处的位置是有区别的。

2.2.2 二叉树的五种基本形态
空二叉树。
只有一个根节点。
根节点只有左树。
根节点只有右树。
根节点既有左树又有右树。
其实这五种形态的二叉树大家还是很容易理解的,那么我们深入探讨一下,假如有三个结点的二叉树,会有几种组合方式?
我们看下图,如果只是按照形态划分的话,那么只有三种形态,分别图1,图2,图5,如果是按照结构划分的话,那就是五种,如下图,图 1 到 图 5 分别代表着不同的二叉树。

2.3 两种特殊的二叉树
2.3.1 满二叉树

满二叉树特点:
- 在一个二叉树种,如果所有分支节点都存在左子树和右子树,并且所有叶子都在同一层上,这样的二叉树称为满二叉树。
- 一棵二叉树,如果每层的结点数都达到最大值,则这棵二叉树就是满二叉树。也就是说,如果一棵二叉树的层数为K,且结点总数是2^k-1 ,则它就是满二叉树。
2.3.2 完全二叉树
完全二叉树是效率很高的数据结构,完全二叉树是由满二叉树而引出来的。对于深度为K的,有n个结点的二叉树,当且仅其每一个结点都与深度为K的满二叉树中编号从0至n-1的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。

2.4 二叉树的性质(由公式推导附加几道练习题)
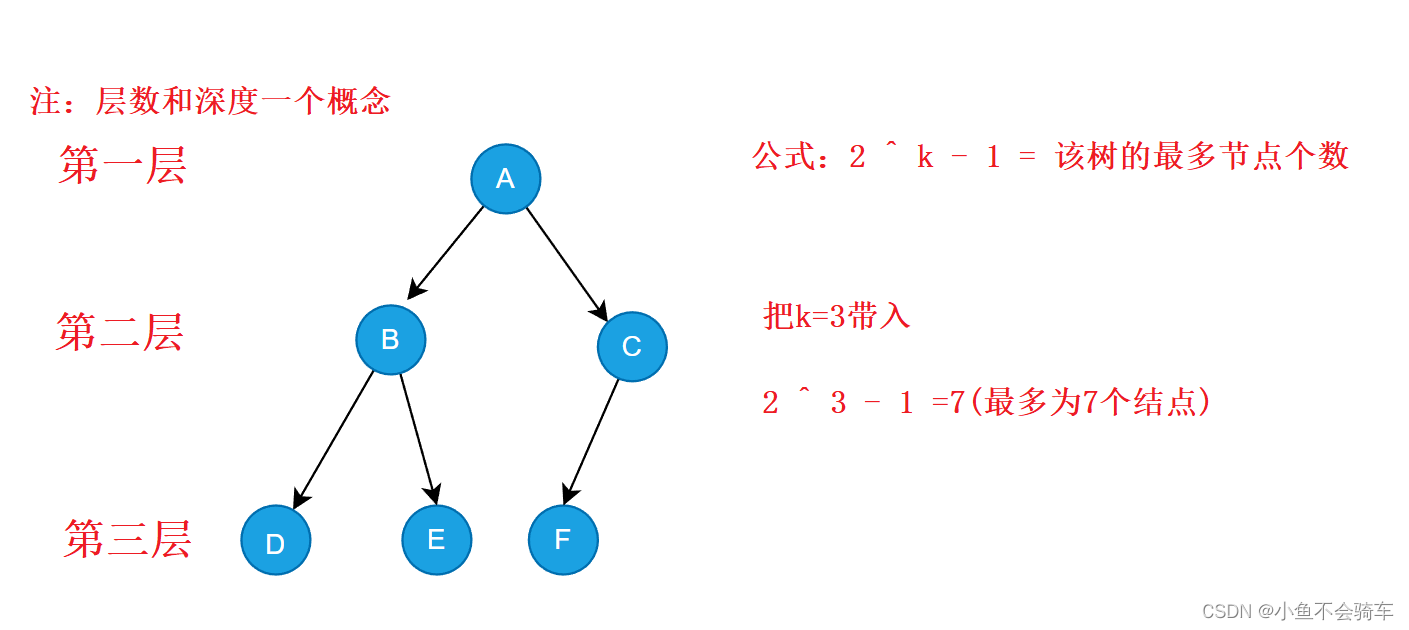
1.若规定根结点的层数为1,则一棵非空二叉树的第i层上最多有2 ^ (i-1) (i>0) 个结点.
论证:

2.若规定只有根结点的二叉树的深度为1,则深度为K的二叉树的最大结点数是 2 ^ k - 1 (k>=0)
论证:
3.(重点)对任何一棵二叉树, 如果其叶结点个数为 n0, 度为2的非叶结点个数为 n2,则有n0=n2+1
论证:
求这个结论时,我们先了解一个知识点就是一个N个节点的树有N-1条边,有了这个知识点之后,我们再进行计算:

4.具有n个结点的完全二叉树的深度k为 log(n + 1)向上取整(默认以2为底,这里忽略不写)
论证:
5.对于具有n个结点的完全二叉树,如果按照从上至下从左至右的顺序对所有节点从0开始编号,则对于序号为i
的结点有:
- 若i>0,双亲序号:(i-1)/2;i=0,i为根结点编号,无双亲结点
- 若2i+1<n,左孩子序号:2i+1,否则无左孩子
- 若2i+2<n,右孩子序号:2i+2,否则无右孩子
举例:

1.某二叉树共有 399 个结点,其中有 199 个度为 2 的结点,则该二叉树中的叶子结点数为( )
A 不存在这样的二叉树
B 200
C 198
D 199
2.在具有 2n 个结点的完全二叉树中,叶子结点个数为( )
A n
B n+1
C n-1
D n/2
3.一个具有767个节点的完全二叉树,其叶子节点个数为()
A 383
B 384
C 385
D 386
4.一棵完全二叉树的节点数为531个,那么这棵树的高度为( )
A 11
B 10
C 8
D 12
答案:
1.B
解析:度为0的结点比度为2的结点多一个,题意说了度为2的结点有199,则度为0的结点为199+1=200
2.A
解析:在有2N个结点的完全二叉树,由于是完全二叉树中,那么只可能存在一个1个度为1的结点,下面就是判断度为1的结点是否存在
我们设总共有N个结点,假设度为1的结点为0
N = n0+n1+n2
N = n0+0+n2 (注:n2=n0-1)
N = 2n0-1(奇数)
所以度为1的结点为0不符合条件
接下来假设度为1的结点有1个
N = n0+n1+n2
N = n0+1+n2
N = 2n0-1+1
N =2n0(偶数,符合条件)
接下来把N替换成题意中的2N,
2N = 2n0
N = n0
最后选A
3.B
该题解法和上述一样,判断是否存在度为1的结点
由于该树是完全二叉树,并且该树的结点为767是奇数,所以可以推出度为1的结点不存在,
所以根据公式:
N = n0+n1+n2
767 = n0+0+n2
767 = 2n0-1
768 = 2n0
384 = n0
4.B
解析:有结点数求高度直接套公式:
log(531+1)向上取整 = 10,
选择B
2.5 二叉树的存储
二叉树的存储结构分为:顺序存储和类似于链表的链式存储。
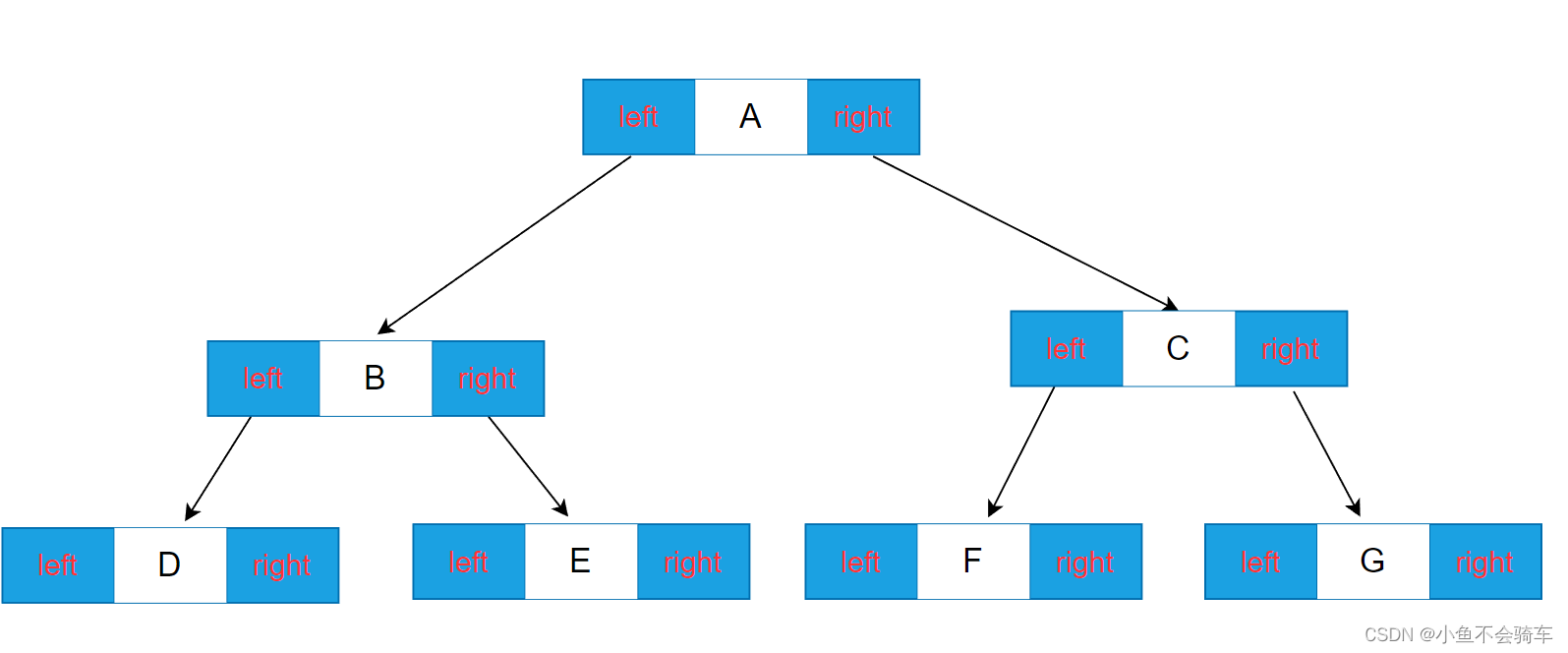
二叉树的链式存储是通过一个一个的节点引用起来的,常见的表示方式有二叉和三叉表示方式,具体如下:
// 孩子表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
}
// 孩子双亲表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用,常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用,常常代表右孩子为根的整棵右子树
Node parent; // 当前节点的根节点
}
我们重点讲解孩子表示法,结构如图
2.6 二叉树的遍历
为了后续方便讲解,我们先创建一个二叉树。
public class BinaryTree<E extends Comparable<E>> {static class Node <E>{Node<E> left;Node<E> right;E val;public Node(E val) {this.val = val;}}public Node<E> root//每个二叉树都需要一个根节点;
}
public static void main(String[] args) {BinaryTree<Character> b = new BinaryTree<>();BinaryTree.Node<Character> A = new BinaryTree.Node<>('A');BinaryTree.Node<Character> B = new BinaryTree.Node<>('B');BinaryTree.Node<Character> C = new BinaryTree.Node<>('C');BinaryTree.Node<Character> D = new BinaryTree.Node<>('D');BinaryTree.Node<Character> E = new BinaryTree.Node<>('E');BinaryTree.Node<Character> F = new BinaryTree.Node<>('F');BinaryTree.Node<Character> G = new BinaryTree.Node<>('G');BinaryTree.Node<Character> H = new BinaryTree.Node<>('H');b.root = A;A.left = B;A.right = C;B.left = D;B.right = E;C.left = F;C.right = G;}
学习二叉树结构,最简单的方式就是遍历。所谓遍历(Traversal)是指沿着某条搜索路线,依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问题(比如:打印节点内容、节点内容加1)。 遍历是二叉树上最重要的操作之一,是二叉树上进行其它运算之基础。
2.6.1 前序遍历
所谓前序遍历就是:根节点-》左子树-》右子树
规则是若二叉树为空,则直接返回,否则先访问根节点,然后遍历左子树,再前序遍历右子树。如下图:

我们通过代码实现以下,并且看一下结果:
// 前序遍历void preOrder(Node <E> root){if(root==null) {return;}System.out.print(root.val+" ");preOrder(root.left);preOrder(root.right);}
运行结果:

2.6.2 中序遍历
中序遍历 左树-》根-》右树
规则:把左树遍历完了之后再去打印根节点,之后再遍历右树,遇到空就返回,否则一直递归下去。
下面就不画动图了(偷个懒哈),我们根据递归的代码带大家一步一步分析(因为需要全部放在同一个图片内,辛苦大家放大观看):

运行结果:

代码如下:
// 中序遍历void inOrder(Node<E>root){if(root==null) {return;}inOrder(root.left);System.out.print(root.val+" ");inOrder(root.right);}
2.6.3 后续遍历
后续遍历:左树-》右树-》根
遍历规则:先遍历左树,左树为空遍历右树,左右为空就打印
如果我们对上述的递归代码熟悉之后,那么我们便可以自己写出后序遍历的递归代码,就是调整一下打印的位置。
// 后序遍历void postOrder(Node <E> root){if(root==null) {return;}postOrder(root.left);postOrder(root.right);System.out.print(root.val+" ");}
2.6.4 层序遍历
关于层序遍历,我们先知道打印的顺序就好,后续会讲解

先将代码放入这里,大家可以看看:
//层序遍历void levelOrder(Node<E> root){//利用队列Queue<Node<E>> queue=new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {Node<E> cur=queue.poll();System.out.print(cur.val+"");if(cur.left!=null)queue.offer(cur.left);if(cur.right!=null)queue.offer(cur.right);}System.out.println();}
2.6.5 前中后遍历的练习题
1.某完全二叉树按层次输出(同一层从左到右)的序列为 ABCDEFGH 。该完全二叉树的前序序列为()
A: ABDHECFG B: ABCDEFGH C: HDBEAFCG D: HDEBFGCA
2.二叉树的先序遍历和中序遍历如下:先序遍历:EFHIGJK;中序遍历:HFIEJKG.则二叉树根结点为()
A: E B: F C: G D: H
3.设一课二叉树的中序遍历序列:badce,后序遍历序列:bdeca,则二叉树前序遍历序列为()
A: adbce B: decab C: debac D: abcde
4.某二叉树的后序遍历序列与中序遍历序列相同,均为 ABCDEF ,则按层次输出(同一层从左到右)的序列为()
A: FEDCBA B: CBAFED C: DEFCBA D: ABCDEF
【参考答案】 1.A 2.A 3.D 4.A
1
1
1
2.7 二叉树的基本操作
2.7.1 获取二叉树结点个数
关于求二叉树的结点个数,我们有两种解法:
子问题思路:
子问题思路就是,将这个树分为根节点和左子树的结点数+右子树的结点数,其中每颗左子树或者右子树又是一个独立的二叉树,再次进行根节点+左子树结点+右子树结点。这里采用从左往右的遍历思路都可以(这里就不画图了,大家可以自己画图思索一下,对于数据结构多画,多想,多写代码是学好数据结构最好的利刃)
//获取树中结点的个数public int size(Node<E> root) {if(root == null) {return 0;}return 1+size(root.left)+size(root.right);}
遍历思路:
遍历思路就是每遍历一个结点就size++,我们采取前序遍历方法(中序,后序都可以,因为每个结点只遍历了一次),遇见根节点就++
// 获取树中节点的个数private int size;// 获取树中节点的个数public void sizePlus(Node<E> root) {if(root==null) {return ;}size++;sizePlus(root.left);sizePlus(root.right);}
2.7.2 获取叶子节点个数
2.7.2.1 遍历思路
所谓叶子节点就是度为0的结点,就说明叶子节点是没有左子树和右子树的,那么我们的代码就可以把判断条件改为,只要是该节点的左树和右树为空,那就count++,代码入下:
// 获取叶子节点的个数,遍历思路//遍历思路,求得叶子个数然后再去调用leaf就可以得到叶子的个数//叶子个数int count = 0;public int getLeafNodeCountPlus(Node<E> root){funcGetLeafNodeCountPlus(root);return count;}public void funcGetLeafNodeCountPlus(Node<E> root) {if(root==null) {return ;}//左子树右子树为空就++if(root.left==null&&root.right==null) {count++;}funcGetLeafNodeCountPlus(root.left);funcGetLeafNodeCountPlus(root.right);}
2.7.2.2 子问题思路
子问题思路就是,左子树的叶子结点+右树的叶子结点,每个左子树或者右子树又是一个新的二叉树.
// 子问题思路-求叶子结点个数public int funcGetLeafNodeCountPlus(Node<E> root) {if(root == null) {return 0;}//左右树为空就返回1if(root.left == null && root.right == null) {return 1;}return funcGetLeafNodeCountPlus(root.left)+funcGetLeafNodeCountPlus(root.right);}
2.7.3 获取第K层结点的个数
所谓获取第K层的结点个数,那么我们可以定义一个记录高度的变量,当我的高度和k相同,并且该节点不为空,那就说明这个结点是第k层的结点。
2.7.3.1 遍历思路
如果是第k层结点就count++
/*** 左树的第n层和右树的第n层* 遍历* @param root k* @return int*/public int count;int getKLevelNodeCount(Node<E> root,int k){funcGetKLevelNodeCount(root,k);return count;}public void funcGetKLevelNodeCount (Node<E> root,int k) {if(k==1&&root!=null) {count++;return;}if(root==null) {return;}getKLevelNodeCount(root.left,k-1);getKLevelNodeCount(root.right,k-1);}
2.7.3.2 子问题思路
左子树的第k层结点+右子树的第k层结点。
/*** 子问题解决求树的第n层的结点* @param root k* @return int*/int getKLevelNodeCountPlus(Node<E> root,int k){if(root==null) {return 0;}if(k==1) {return 1;}//左树第k层结点+右树第k层结点return getKLevelNodeCountPlus(root.left,k-1)+ getKLevelNodeCountPlus(root.right,k-1);}
2.7.4 获取二叉树的高度
获取二叉树的高度这道题,上述讲到了(树的高度或深度:树中结点的最大层次)因为要找到树的最大层次,所以第一件事就是找到叶子结点然后开始返回,但是并不是所有的叶子节点都在最后一层(如图1),所以我们可以思考一下,可不可以将获取树的高度这个问题分解一下,改成获取左子树的高度和右子树的高度,然后对比哪个高,就返回哪个并且加上根节点,因为根节点本身也占一层。那调用左子树的高度时,又变成了获取该树的左子树和右子树深度的最大值再加上当前的根节点。那么我们可以根据这个思路去写代码:

// 获取二叉树的高度/*** 比较左树和右树的高度* @param root* @return*/public int getHeight(Node<E> root){if(root==null) {return 0;}int a=getHeight(root.left);int b=getHeight(root.right);//左树高度和右树高度求最大值再+1return Math.max(a+1, b+1);}
2.7.5 检测value的元素是否存在
采用遍历思路,当根节点的值为 val 时就返回 true ,如果根节点为空说明没有找到就返回 false ,如果根节点不为null,并且还没有找到val,那么继续去左树和右树中查找,如果找到了就返回true,最后的返回值是左子树| | 右子树,只要有一个为真就返回真!
// 检测值为value的元素是否存在public boolean find(Node<E> root, E val){if(root==null) {return false;}if(root.val==val) {return true;}//遍历当前结点和左子树和右子树boolean a1= find(root.left,val);boolean a2 = find(root.right,val);return a1||a2;}
2.7.6 层序遍历
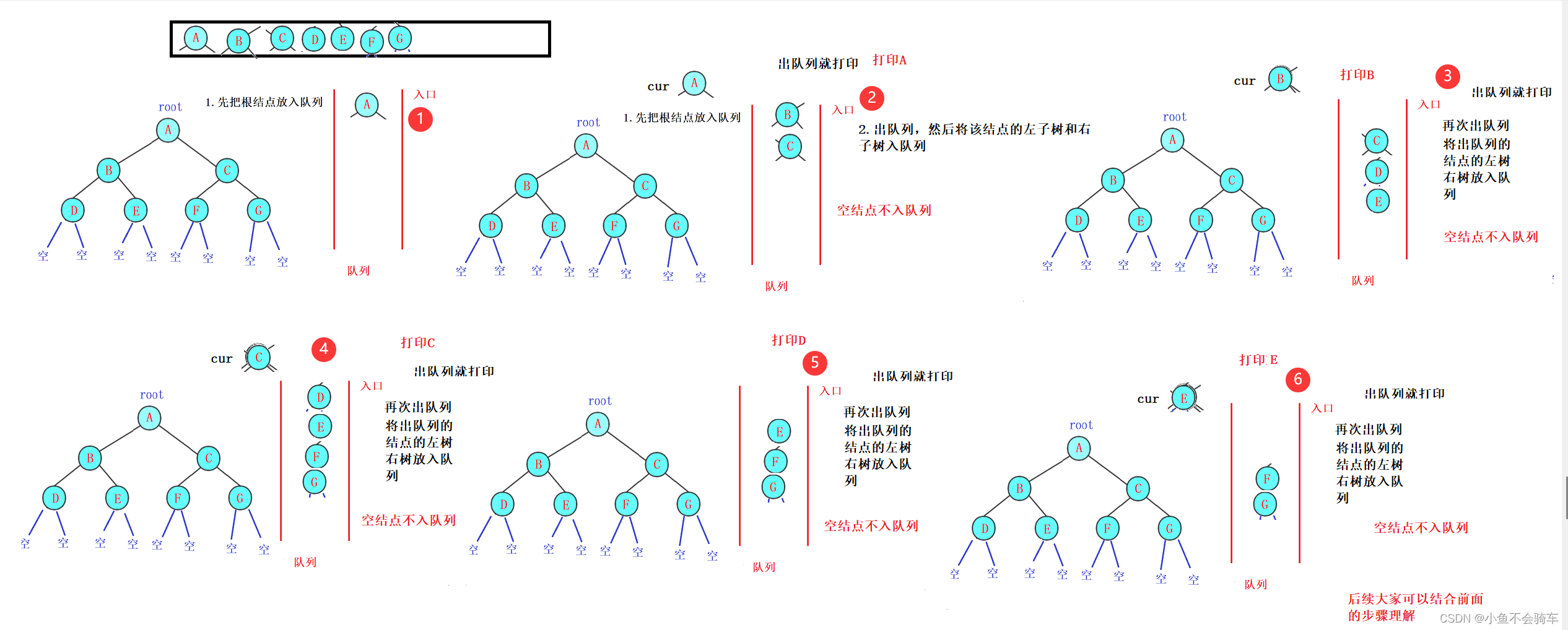
层序遍历上述也介绍到了,就是从左到右,从上到下遍历,遍历完这一层所有的结点,再去遍历下一层的结点。
对于层序遍历我们需要借助一个工具,就是队列,我们来看图:
代码如下:
//层序遍历void levelOrder(Node<E> root){//利用队列Queue<Node<E>> queue=new LinkedList<>();queue.offer(root);while (!queue.isEmpty()) {Node<E> cur=queue.poll();System.out.print(cur.val+"");if(cur.left!=null)queue.offer(cur.left);if(cur.right!=null)queue.offer(cur.right);}System.out.println();}
2.7.7 判断一颗树是不是完全二叉树
关于完全二叉树的介绍上述有讲到,判断完全二叉树也是需要一个工具,依旧是队列,上述的队列实现了层序遍历,那么我们可以在这个层序遍历的基础上给升级一下,我们通过完全二叉树和非完全二叉树来对比一下:
完全二叉树:

非完全二叉树:
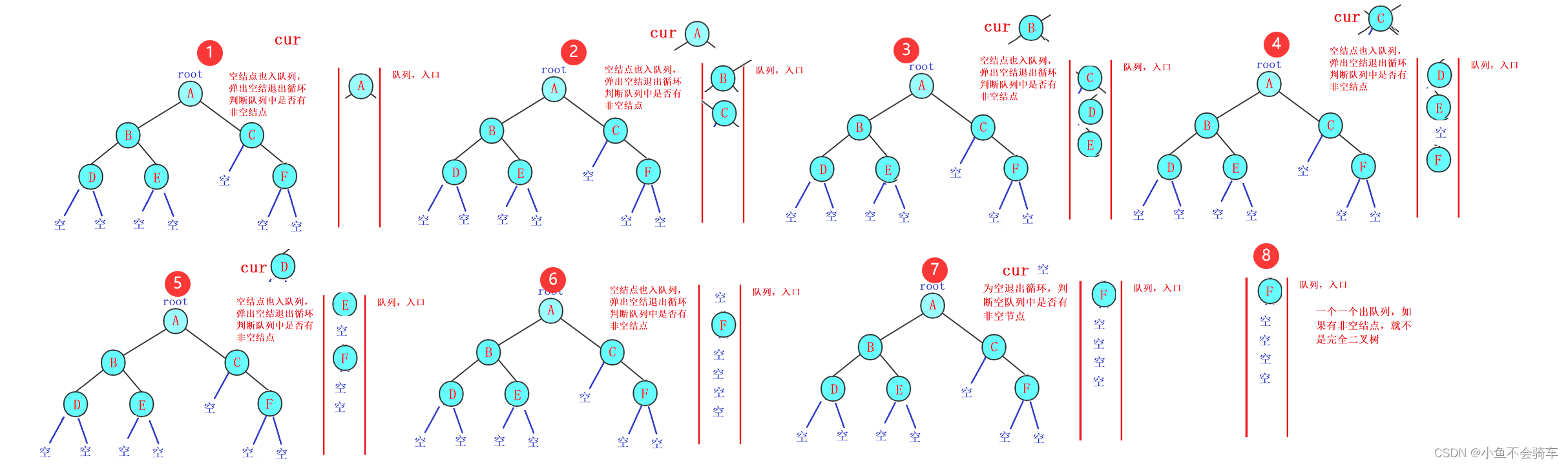
根据对比我们发现,完全二叉树的队列,当出第一个空结点后,其余结点都是空结点,但是非完全二叉树的队列,在弹出第一个空结点后,其余结点一定有非空结点。
代码入下:
// 判断一棵树是不是完全二叉树boolean isCompleteTree(Node<E> root){//队列实现Deque<Node<E>> queue=new LinkedList<>();queue.offer(root);//为空退出循环while (queue.peek()!=null){Node<E> cur=queue.poll();queue.offer(cur.left);queue.offer(cur.right);}//判断剩余结点是否包含非空节点for (int i = 0; i < queue.size(); i++) {if(queue.poll()!=null) {return false;}}return true;}
相关文章:

java实现二叉树(一文带你详细了解二叉树的)
🎇🎇🎇作者: 小鱼不会骑车 🎆🎆🎆专栏: 《数据结构》 🎓🎓🎓个人简介: 一名专科大一在读的小比特,努力学习编程是我唯一…...
学弟学妹少走弯路,超完整算法刷题路线出炉
大家好,我是帅地。 本篇文章主要讲解下面三个事: 1、自己学习算法的一些经历 2、大家学习算法存在的一些普遍问题 3、给大家规划的算法刷题路线 一、算法学习往事 记得当初学了 C 语言就开始刷题了,刷题倒不是面试,而是为了…...
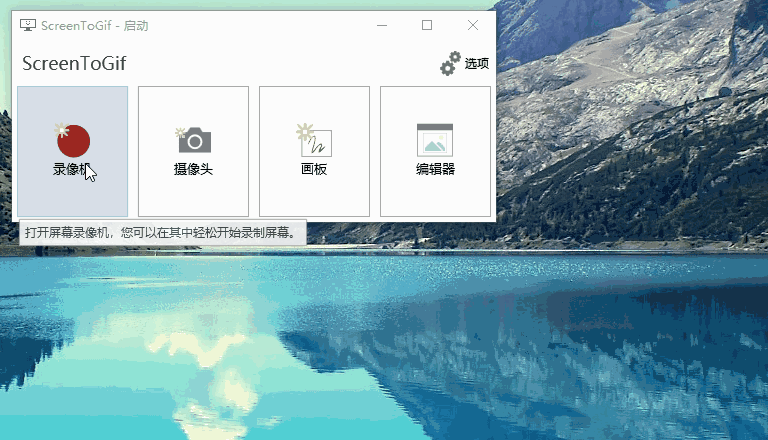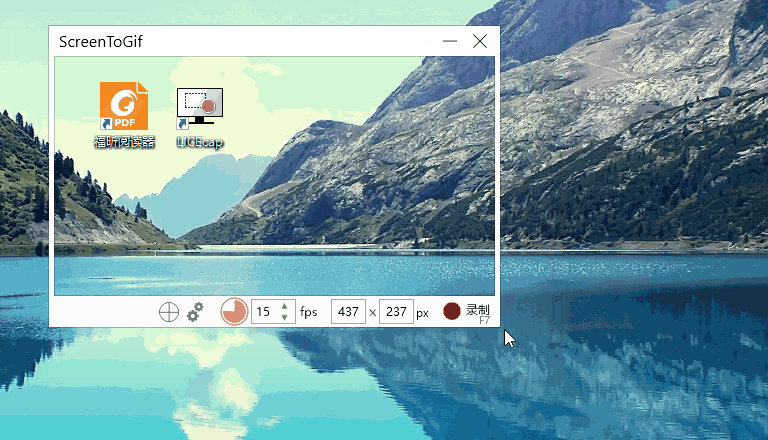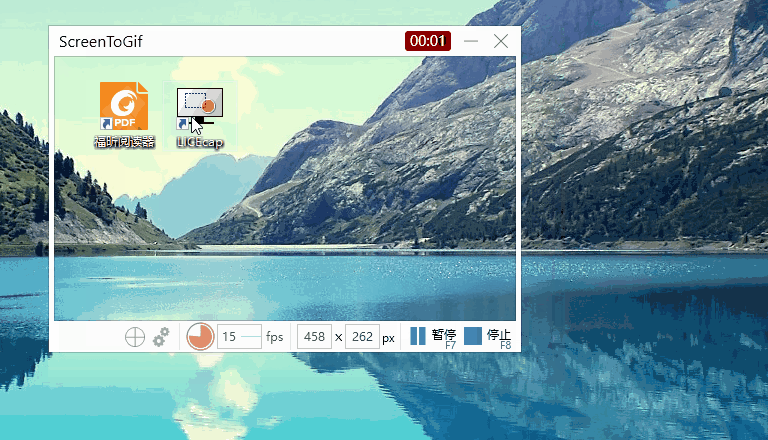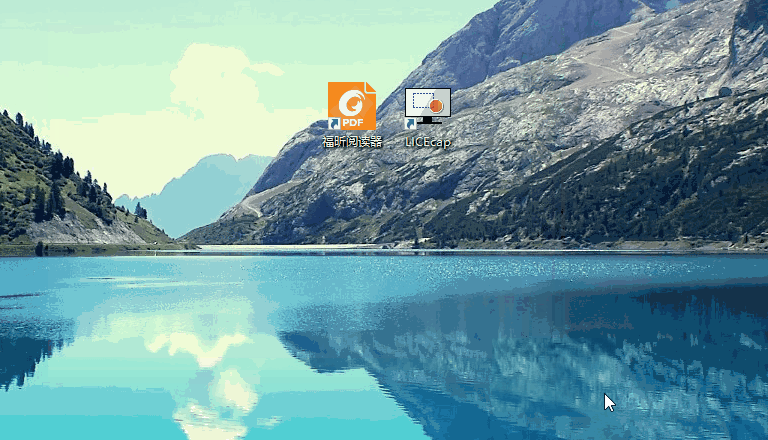
Windows截取gif动态图的软件 ScreenToGif 的安装、使用教程
一、概述 👉GIF(Graphics Interchange Format),又称图形交换格式,是一种公用的图像文件格式标准,于1987年由Compu Serve公司成功研发并推出。 👉GIF用于以超文本标志语言方式显示索引彩色图像&a…...

C++程序设计——多态:虚函数、抽象类、虚函数表
注:以下示例均是在VS2019环境下 一、多态的概念 通俗来讲,多态就是多种形态,当不同的对象去完成某个行为时,会产生出不同的状态。即不同继承关系的类对象,去调用同一函数时,产生不同的行为。 比如”叫“这…...
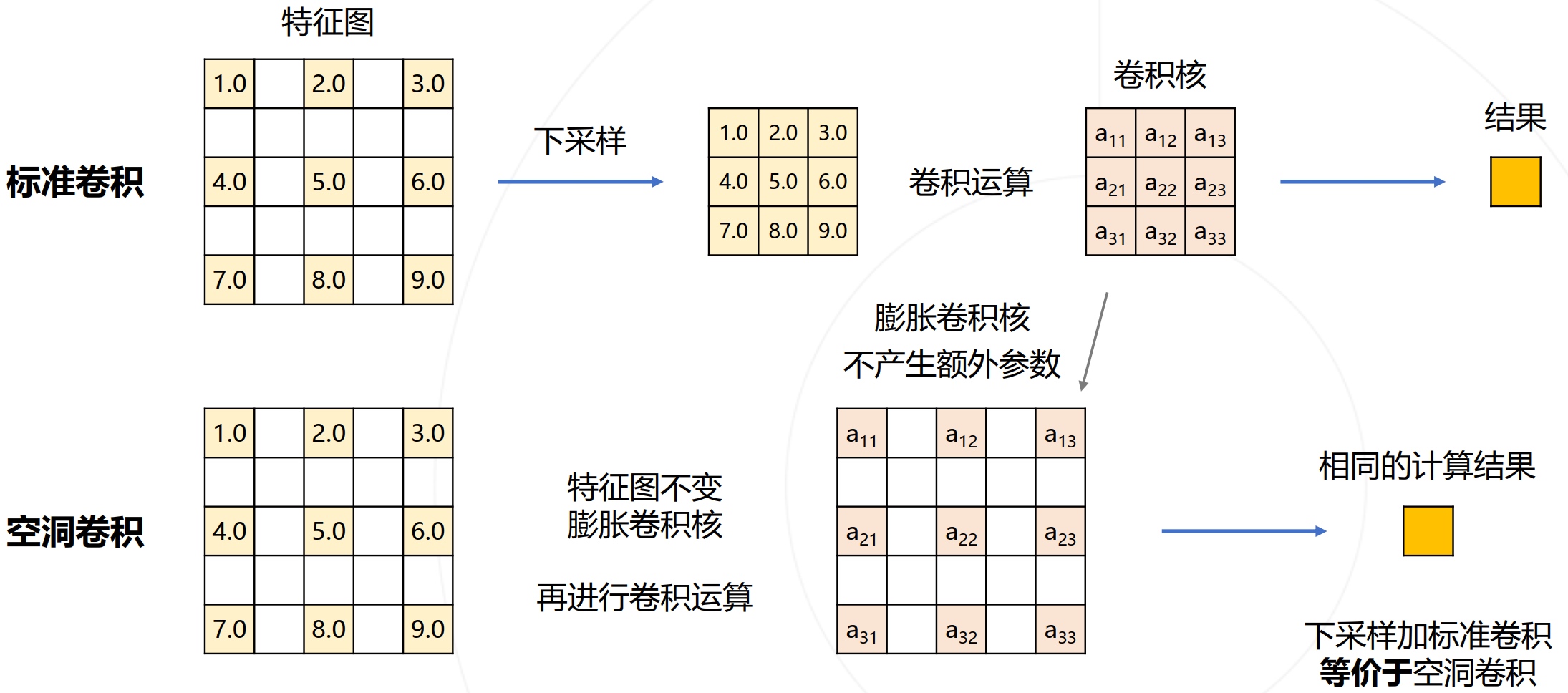
OpenMMLab AI实战营 第6课 语义分割与MMSegmentation
第6课 语义分割与MMSegmentation 1. 语义分割简介 任务:将图像按照物体的类别分割成不同的区域,等价于对每个像素进行分类应用 无人驾驶人像分割智能遥感医疗影像分析 语义分割 vs 实例分割 vs 全景分割 语义分割:仅考虑像素的类别…...

产业互联网是对互联网的衍生和进化,也是一次重塑和再造
互联网并不仅仅只是充当撮合和中介的角色,它应当具备更多的功能和意义。只有这样,它的发展才能够真正全面和完善。产业互联网的衍生和出现,正是在互联网进化的基础之上出现的。这是我们看到之所以会有那么多的互联网玩家投身到产业互联网的浪…...
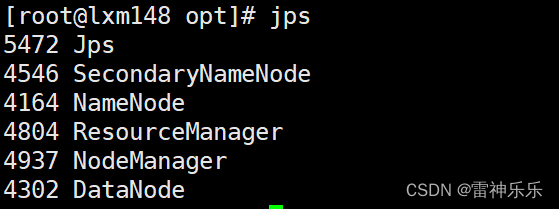
Shell脚本之——Hadoop3单机版安装
目录 1.解压 2.文件重命名 3.配置环境变量 4.hadoop-env.sh 5.core-site.xml 6. hdfs-site.xml 7. mapred-site.xml 8.yarn-site.xml 9.完整脚本代码(注意修改主机名) 10.重启环境变量 11.初始化 12.启动服务 13.jps查询节点 1.解压 tar -zxf /opt/install/hadoo…...
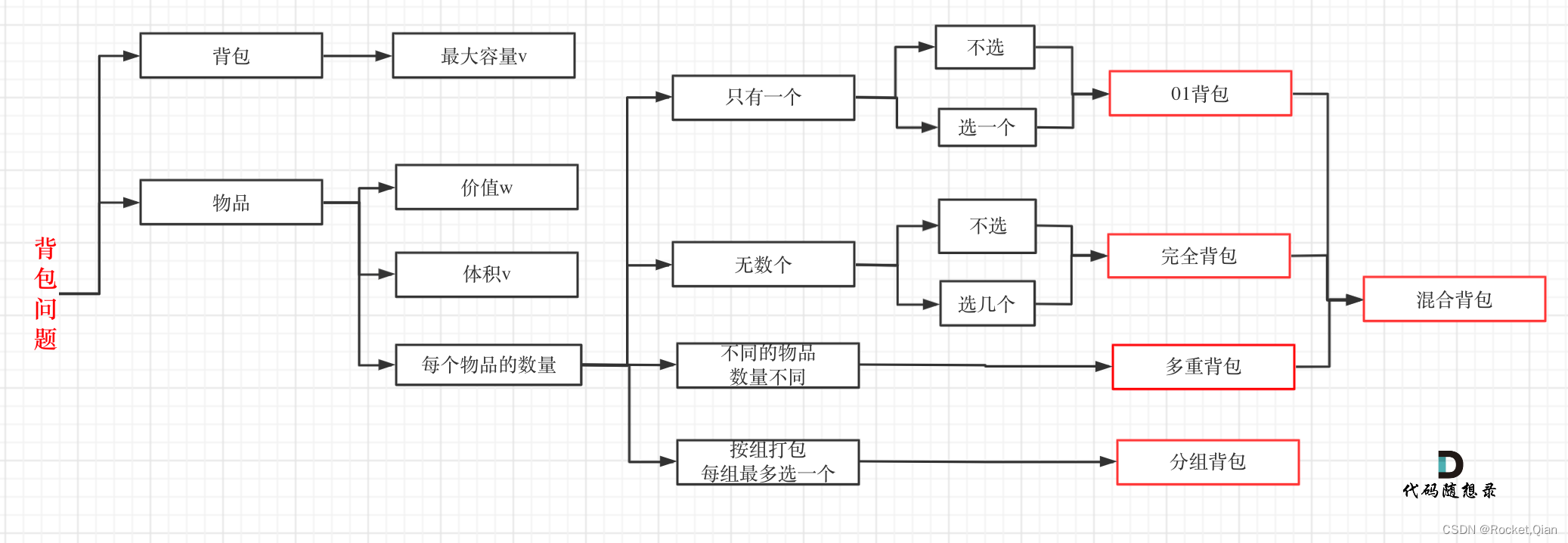
代码随想录NO39 |0-1背包问题理论基础 416.分割等和子集
0-1背包问题理论基础 分割等和子集1. 0-1背包问题理论基础(二维数组实现)2. 0-1背包问题理论基础 二(一维数组实现)1. 0-1背包问题理论基础(二维数组实现) 背包问题一般分为这几种: 0-1背包问题:有n件物品和一个最多能背重量为w…...
FITC-PEG-FA,荧光素-聚乙二醇-叶酸,FA-PEG-FITC,实验室科研试剂,提供质量检测
FITC-PEG-FA,荧光素-聚乙二醇-叶酸 中文名称:荧光素-聚乙二醇-叶酸 英文名称:FITC-PEG-FA 英文别名:Fluorescein-PEG-Folic Acid 性状:基于不同的分子量,呈白色/类白色固体,或粘稠液体。 溶…...

简洁易懂:源码+实战讲解Redisson并发锁及看门狗自动续期
1 缘起 有一次同事问Redisson存储的键是否为hash? 我当时,没有看Redisson的相关源码,只知道应用, 所以没有办法回答,于是开始看看Redisson实现的源码, 顺便写了一个单机Redisson测试, 发现Redi…...
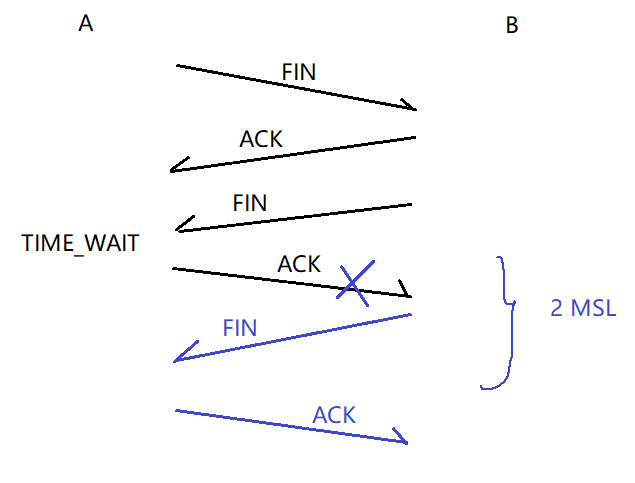
TCP 三次握手和四次挥手
✏️作者:银河罐头 📋系列专栏:JavaEE 🌲“种一棵树最好的时间是十年前,其次是现在” 目录TCP 建立连接(三次握手)为啥不能是 4 次?为啥不能是 2 次?三次握手的意义:TCP 断开连接(四…...
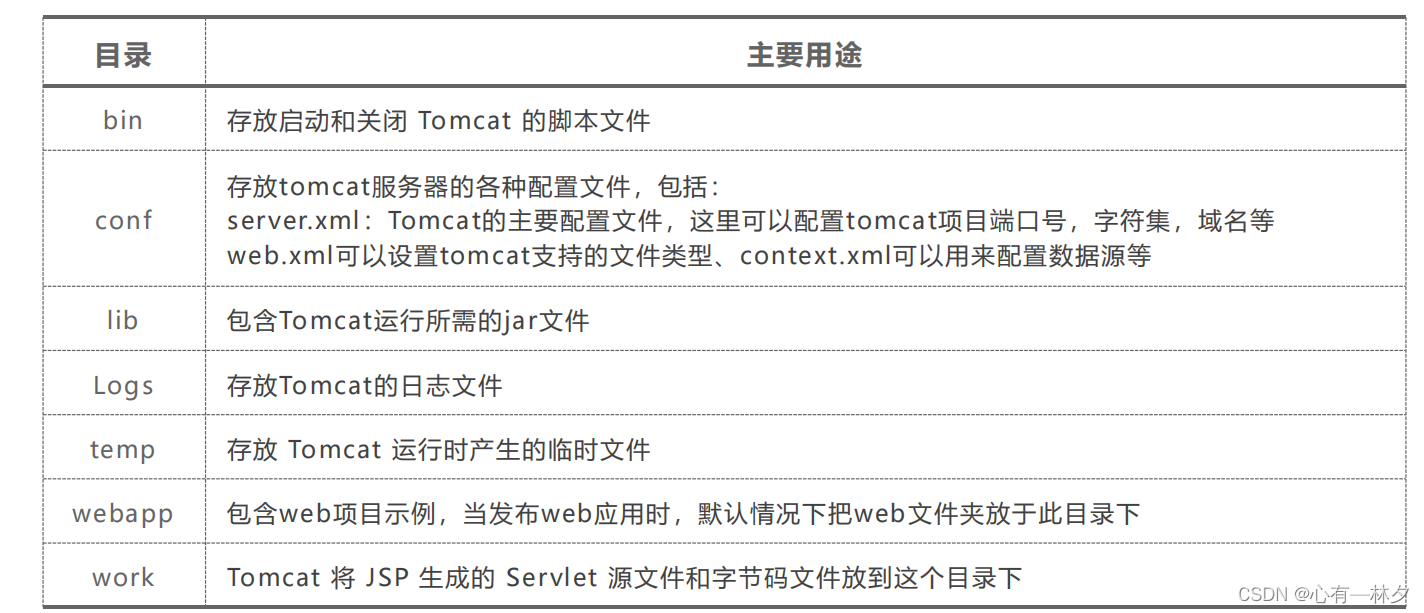
JavaWeb复习
JavaWeb复习一.概述1.概念2.B/S和C/S 架构二.HTTP通信协议概述1.概念2.HTTP1.0 与 HTTP1.1 版本3.HTTP 协议组成4.常见状态码5.GET 与 POST 请求方式三.Tomcat1.Web服务器介绍2.安装(Windows)3.Tomcat目录结构4.server.xml部分配置解释四.Servlet1.概念2…...

P14 PyTorch AutoGrad
前言:激活函数与loss的梯度PyTorch 提供了Auto Grad 功能,这里系统讲解一下torch.autograd.grad系统的工作原理,了解graph 结构目录:1: require_grad False2: require_grad True3: 多层bakcward 原理4: in…...

前端报表如何实现无预览打印解决方案或静默打印
在前端开发中,除了将数据呈现后,我们往往需要为用户提供,打印,导出等能力,导出是为了存档或是二次分析,而打印则因为很多单据需要打印出来作为主要的单据来进行下一环节的票据支撑, 而前端打印可…...

Operating System Course 2 - My OS
Computer Startup process上一篇:http://t.csdn.cn/XfUKt 讲到这个启动设备的第一个扇区:引导扇区。那么引导扇区的代码长什么样子?这里得看引导扇区代码源文件bootsect.s(.s后缀文件为用汇编语言编写的源代码文件)。另…...

离散数学 课时一 命题逻辑的基本概念
1 命题 1、命题:可以判断其真值的陈述句 2、真值:真或者假(1或者0) 3、真命题:真值为真的命题 4、假命题:真值为假的命题 5、原子命题:不可以再被分解成更简单的命题 6、复合命题:由原子命题通过联结词联结…...
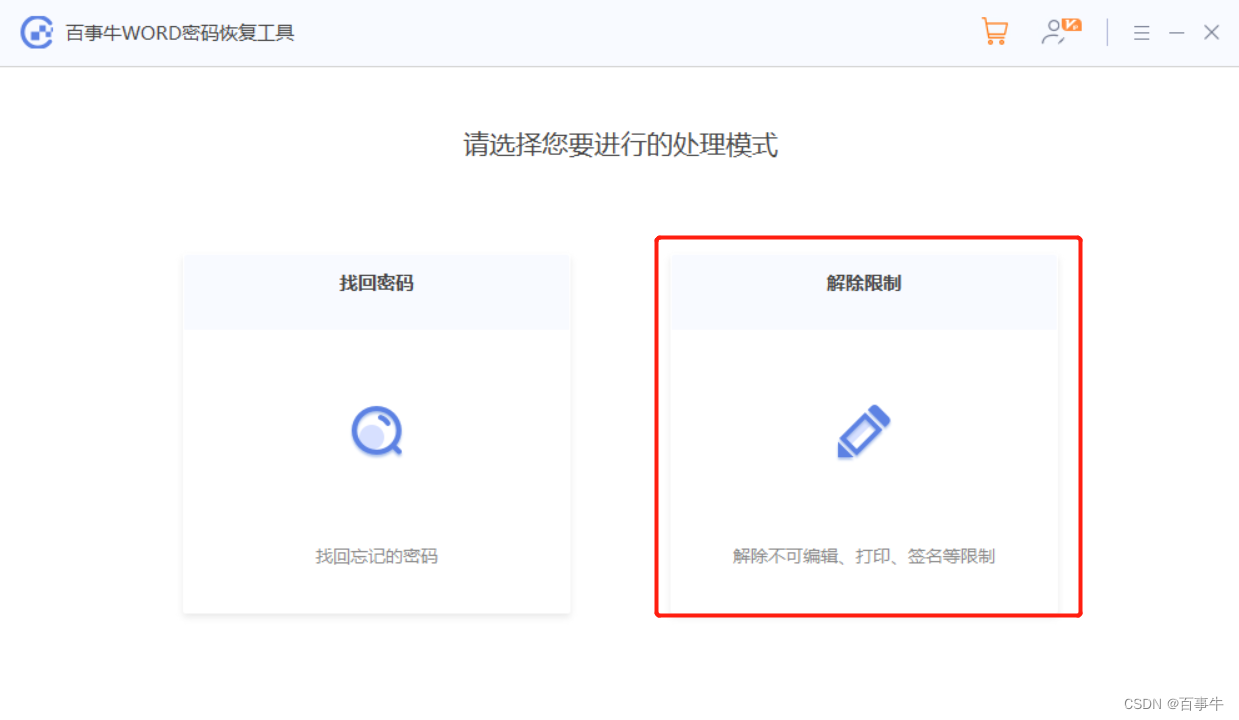
Word文档带有权限密码怎么办?
Word文档的权限密码指的是什么?其实这是Word文档的保护方法之一,具体指Word文档的编辑、修改受到了限制,需要输入密码才能进行。 设置了权限密码的Word文档还是可以直接打开,只有当需要编辑或者修改内容的时候,才会发…...
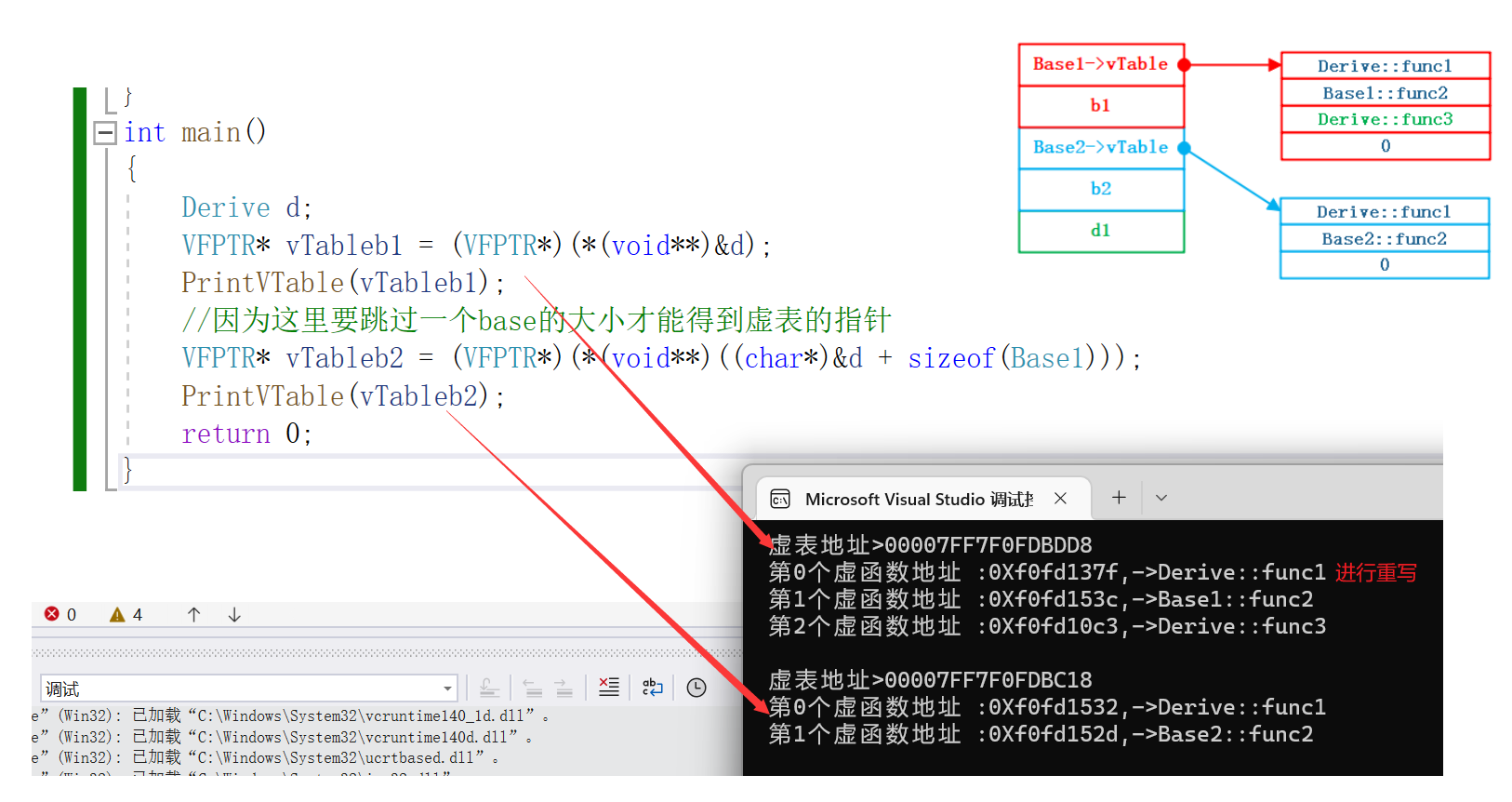
C++多态
1. 多态的概念1.1 概念多态的概念:通俗来说,就是多种形态,具体点就是去完成某个行为,当不同的对象去完成时会产生出不同的状态举个例子:比如买票这个行为,当普通人买票时,是全价买票;…...

访问学者如何申请美国J1签证?
一、申请美国J1签证的步骤: 第一步:填写I901表。 填写I901表会收取SERVIS费用180美元,可以用VISA/Master卡直接网上支付。填完后打印收据单或者存成PDF后续再打印,记下I901收据编号。 第二步:DS-160表填写。 填写DS-…...
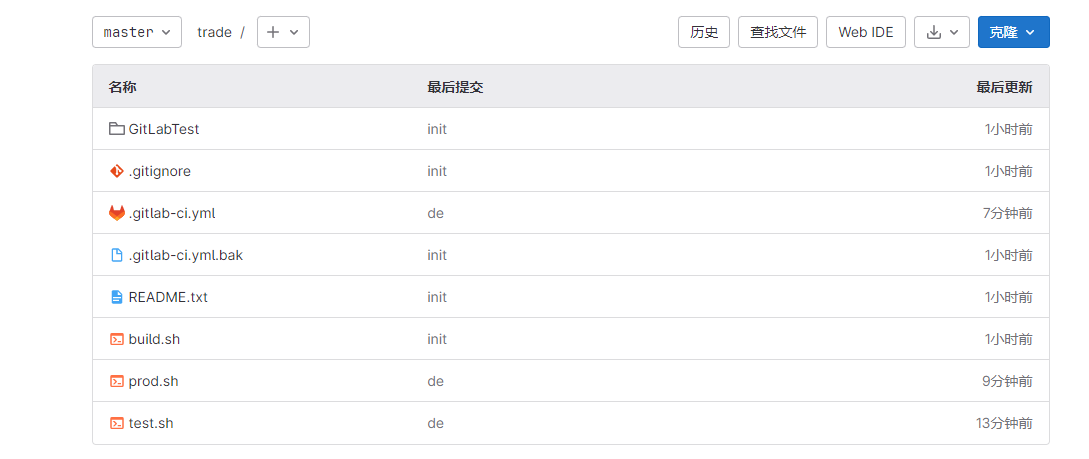
使用gitlab ci/cd来发布一个.net 项目
gitlab runner的安装和基本使用:https://bear-coding.blog.csdn.net/article/details/120591711安装并给项目配置完gitlab runner后再操作后面步骤。实现目标:master分支代码有变更的时候自动构建build。当开发人员在gitlab上给项目打一个tag标签分支的时候自动触发…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

RocketMQ延迟消息机制
两种延迟消息 RocketMQ中提供了两种延迟消息机制 指定固定的延迟级别 通过在Message中设定一个MessageDelayLevel参数,对应18个预设的延迟级别指定时间点的延迟级别 通过在Message中设定一个DeliverTimeMS指定一个Long类型表示的具体时间点。到了时间点后…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

基于当前项目通过npm包形式暴露公共组件
1.package.sjon文件配置 其中xh-flowable就是暴露出去的npm包名 2.创建tpyes文件夹,并新增内容 3.创建package文件夹...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

