代码随想录NO39 |0-1背包问题理论基础 416.分割等和子集
0-1背包问题理论基础 分割等和子集
- 1. 0-1背包问题理论基础(二维数组实现)
- 2. 0-1背包问题理论基础 二(一维数组实现)
1. 0-1背包问题理论基础(二维数组实现)
背包问题一般分为这几种:
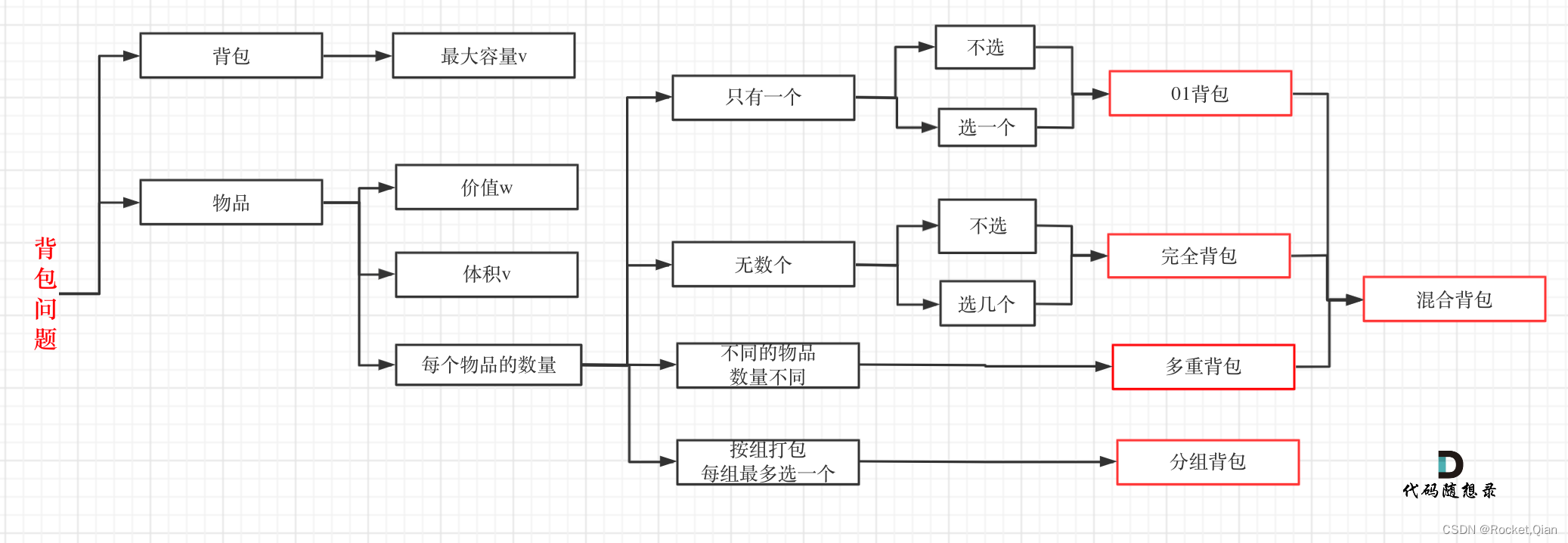
0-1背包问题:有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i],得到的价值是value[i] 。每件物品只能用一次,求解将哪些物品装入背包里物品价值总和最大。
二维dp数组01背包
- 确定dp数组以及下标的含义
对于背包问题,有一种写法, 是使用二维数组,即dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。 - 确定递推公式
再回顾一下dp[i][j]的含义:从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
那么可以有两个方向推出来dp[i][j],- 不放物品i:由dp[i - 1][j]推出,即背包容量为j,里面不放物品i的最大价值,此时dp[i][j]就是dp[i - 1][j]。(其实就是当物品i的重量大于背包j的重量时,物品i无法放进背包中,所以被背包内的价值依然和前面相同。)
- 放物品i:由dp[i - 1][j - weight[i]]推出,dp[i - 1][j - weight[i]] 为背包容量为j - weight[i]的时候不放物品i的最大价值,那么dp[i - 1][j - weight[i]] + value[i] (物品i的价值),就是背包放物品i得到的最大价值
所以递归公式: dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);
- dp数组如何初始化
- 确定遍历顺序 先遍历物品更好理解。
- 举例推导dp数组
def test_2_wei_bag_problem1(bag_size, weight, value) -> int: rows, cols = len(weight), bag_size + 1dp = [[0 for _ in range(cols)] for _ in range(rows)]# 初始化dp数组. for i in range(rows): dp[i][0] = 0first_item_weight, first_item_value = weight[0], value[0]for j in range(1, cols): if first_item_weight <= j: dp[0][j] = first_item_value# 更新dp数组: 先遍历物品, 再遍历背包. for i in range(1, len(weight)): cur_weight, cur_val = weight[i], value[i]for j in range(1, cols): if cur_weight > j: # 说明背包装不下当前物品. dp[i][j] = dp[i - 1][j] # 所以不装当前物品. else: # 定义dp数组: dp[i][j] 前i个物品里,放进容量为j的背包,价值总和最大是多少。dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - cur_weight]+ cur_val)print(dp)if __name__ == "__main__": bag_size = 4weight = [1, 3, 4]value = [15, 20, 30]test_2_wei_bag_problem1(bag_size, weight, value)
2. 0-1背包问题理论基础 二(一维数组实现)
def test_1_wei_bag_problem():weight = [1, 3, 4]value = [15, 20, 30]bag_weight = 4# 初始化: 全为0dp = [0] * (bag_weight + 1)# 先遍历物品, 再遍历背包容量for i in range(len(weight)):for j in range(bag_weight, weight[i] - 1, -1):# 递归公式dp[j] = max(dp[j], dp[j - weight[i]] + value[i])print(dp)test_1_wei_bag_problem()
416. 分割等和子集
给你一个 只包含正整数 的非空数组 nums 。请你判断是否可以将这个数组分割成两个子集,使得两个子集的元素和相等。
只有确定了如下四点,才能把01背包问题套到本题上来。
- 背包的体积为sum / 2
- 背包要放入的商品(集合里的元素)重量为 元素的数值,价值也为元素的数值
- 背包如果正好装满,说明找到了总和为 sum / 2 的子集。
- 背包中每一个元素是不可重复放入。
以上分析完,我们就可以套用01背包,来解决这个问题了。
class Solution:def canPartition(self, nums: List[int]) -> bool:target = sum(nums)if target % 2 == 1: return Falsetarget //= 2dp = [0] * 10001for i in range(len(nums)):for j in range(target, nums[i] - 1, -1):dp[j] = max(dp[j], dp[j - nums[i]] + nums[i])return target == dp[target]
相关文章:

代码随想录NO39 |0-1背包问题理论基础 416.分割等和子集
0-1背包问题理论基础 分割等和子集1. 0-1背包问题理论基础(二维数组实现)2. 0-1背包问题理论基础 二(一维数组实现)1. 0-1背包问题理论基础(二维数组实现) 背包问题一般分为这几种: 0-1背包问题:有n件物品和一个最多能背重量为w…...
FITC-PEG-FA,荧光素-聚乙二醇-叶酸,FA-PEG-FITC,实验室科研试剂,提供质量检测
FITC-PEG-FA,荧光素-聚乙二醇-叶酸 中文名称:荧光素-聚乙二醇-叶酸 英文名称:FITC-PEG-FA 英文别名:Fluorescein-PEG-Folic Acid 性状:基于不同的分子量,呈白色/类白色固体,或粘稠液体。 溶…...

简洁易懂:源码+实战讲解Redisson并发锁及看门狗自动续期
1 缘起 有一次同事问Redisson存储的键是否为hash? 我当时,没有看Redisson的相关源码,只知道应用, 所以没有办法回答,于是开始看看Redisson实现的源码, 顺便写了一个单机Redisson测试, 发现Redi…...
TCP 三次握手和四次挥手
✏️作者:银河罐头 📋系列专栏:JavaEE 🌲“种一棵树最好的时间是十年前,其次是现在” 目录TCP 建立连接(三次握手)为啥不能是 4 次?为啥不能是 2 次?三次握手的意义:TCP 断开连接(四…...
JavaWeb复习
JavaWeb复习一.概述1.概念2.B/S和C/S 架构二.HTTP通信协议概述1.概念2.HTTP1.0 与 HTTP1.1 版本3.HTTP 协议组成4.常见状态码5.GET 与 POST 请求方式三.Tomcat1.Web服务器介绍2.安装(Windows)3.Tomcat目录结构4.server.xml部分配置解释四.Servlet1.概念2…...

P14 PyTorch AutoGrad
前言:激活函数与loss的梯度PyTorch 提供了Auto Grad 功能,这里系统讲解一下torch.autograd.grad系统的工作原理,了解graph 结构目录:1: require_grad False2: require_grad True3: 多层bakcward 原理4: in…...

前端报表如何实现无预览打印解决方案或静默打印
在前端开发中,除了将数据呈现后,我们往往需要为用户提供,打印,导出等能力,导出是为了存档或是二次分析,而打印则因为很多单据需要打印出来作为主要的单据来进行下一环节的票据支撑, 而前端打印可…...

Operating System Course 2 - My OS
Computer Startup process上一篇:http://t.csdn.cn/XfUKt 讲到这个启动设备的第一个扇区:引导扇区。那么引导扇区的代码长什么样子?这里得看引导扇区代码源文件bootsect.s(.s后缀文件为用汇编语言编写的源代码文件)。另…...

离散数学 课时一 命题逻辑的基本概念
1 命题 1、命题:可以判断其真值的陈述句 2、真值:真或者假(1或者0) 3、真命题:真值为真的命题 4、假命题:真值为假的命题 5、原子命题:不可以再被分解成更简单的命题 6、复合命题:由原子命题通过联结词联结…...
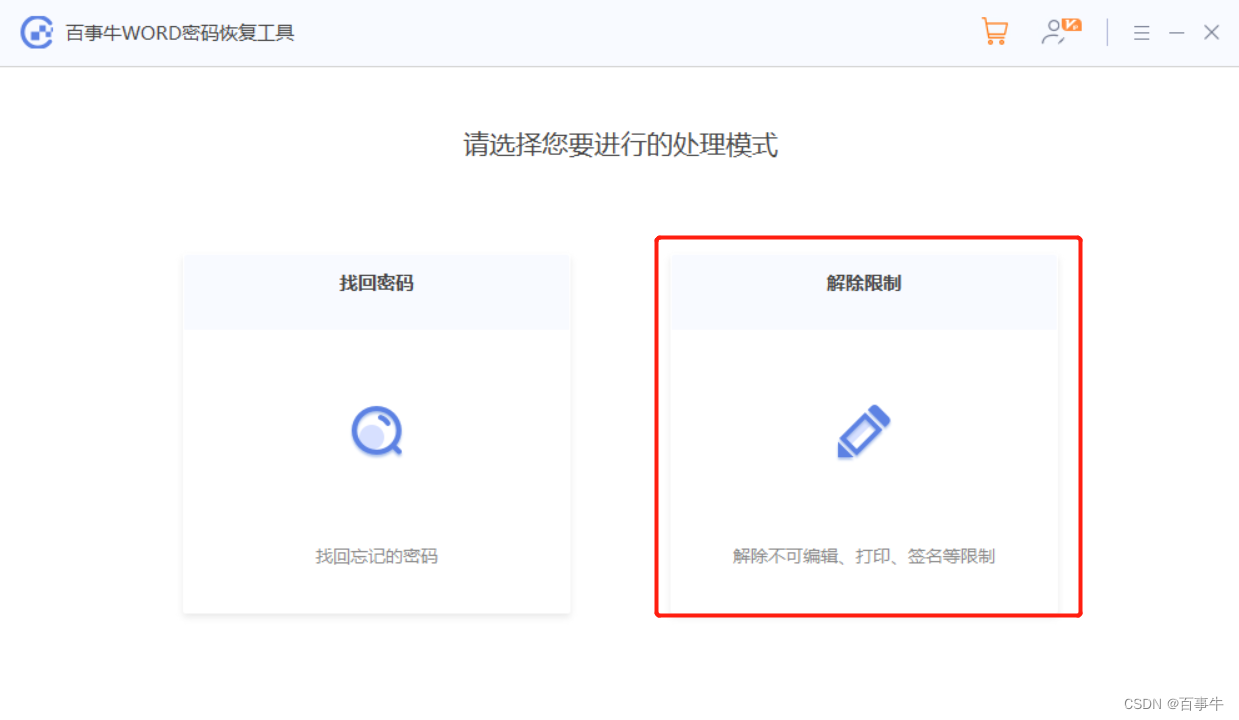
Word文档带有权限密码怎么办?
Word文档的权限密码指的是什么?其实这是Word文档的保护方法之一,具体指Word文档的编辑、修改受到了限制,需要输入密码才能进行。 设置了权限密码的Word文档还是可以直接打开,只有当需要编辑或者修改内容的时候,才会发…...
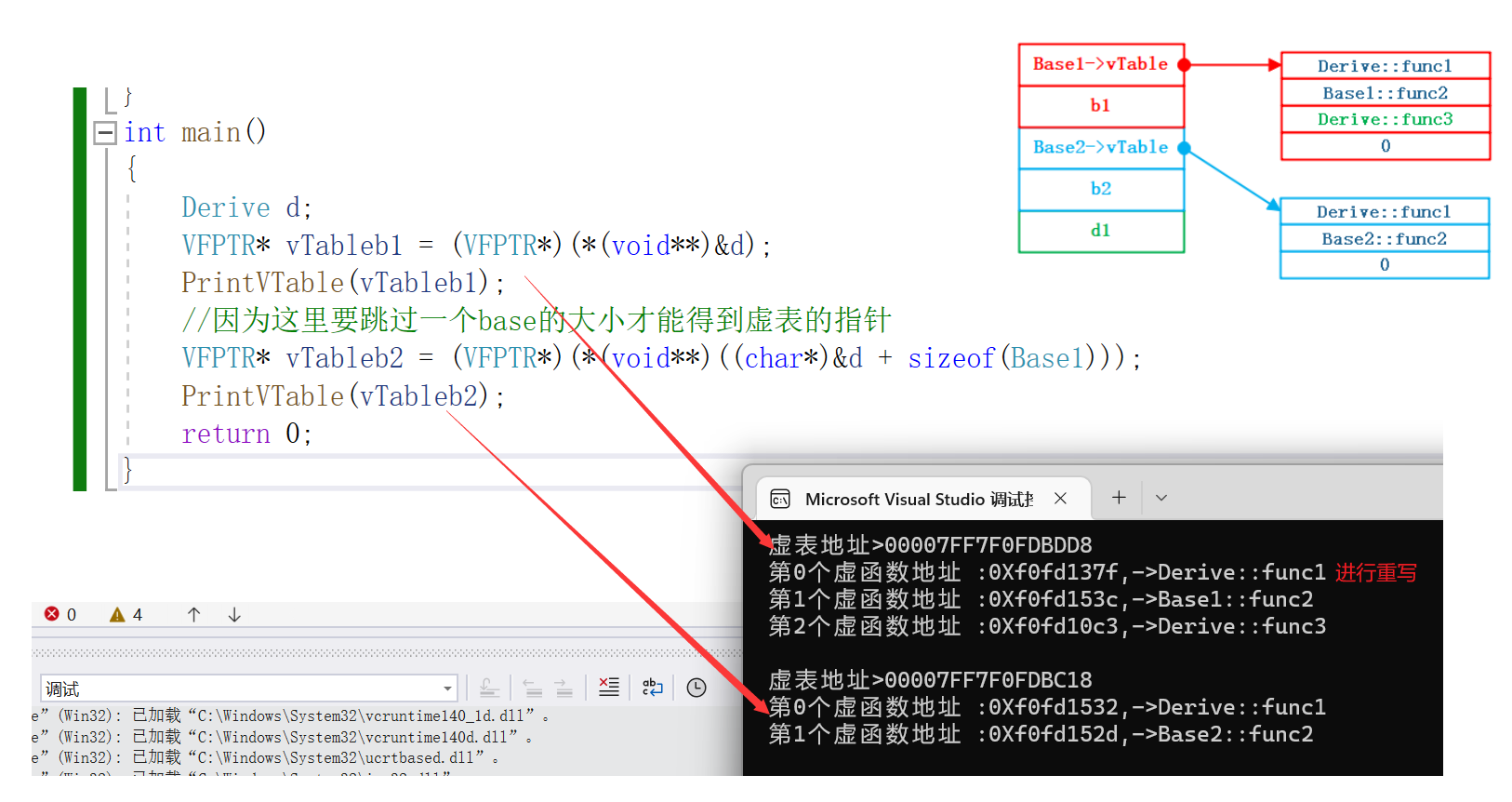
C++多态
1. 多态的概念1.1 概念多态的概念:通俗来说,就是多种形态,具体点就是去完成某个行为,当不同的对象去完成时会产生出不同的状态举个例子:比如买票这个行为,当普通人买票时,是全价买票;…...

访问学者如何申请美国J1签证?
一、申请美国J1签证的步骤: 第一步:填写I901表。 填写I901表会收取SERVIS费用180美元,可以用VISA/Master卡直接网上支付。填完后打印收据单或者存成PDF后续再打印,记下I901收据编号。 第二步:DS-160表填写。 填写DS-…...
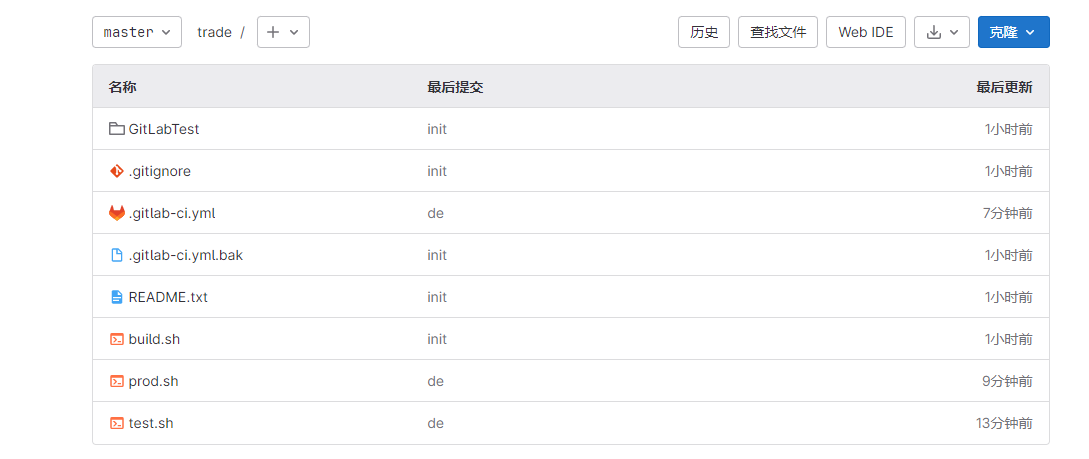
使用gitlab ci/cd来发布一个.net 项目
gitlab runner的安装和基本使用:https://bear-coding.blog.csdn.net/article/details/120591711安装并给项目配置完gitlab runner后再操作后面步骤。实现目标:master分支代码有变更的时候自动构建build。当开发人员在gitlab上给项目打一个tag标签分支的时候自动触发…...

笔试题-2023-蔚来-数字芯片设计【纯净题目版】
回到首页:2023 数字IC设计秋招复盘——数十家公司笔试题、面试实录 推荐内容:数字IC设计学习比较实用的资料推荐 题目背景 笔试时间:2022.08.24应聘岗位:校招-芯片逻辑综合工程师-智能硬件笔试时长:90min笔试平台:nowcoder牛客网题目类型:不定项选择题(15道)、填空题…...

ThreadLocal 详解
ThreadLocal简介JDK源码对ThreadLocal类的注释如下:ThreadLocal提供线程局部变量,使得每个线程都有自己的、独立初始化的变量副本ThreadLocal实例通常是类中的private static字段,用于将状态与线程相关联,如用户ID、事务ID只要线程…...

【Java 面试合集】重写以及重载有什么区别能简单说说嘛
重写以及重载有什么区别能简单说说嘛 前述 这是一道非常基础的面试题,我们在回答的过程中一定要逐一横向比较。 从方法的 修饰符,返回值,方法名,含义,参数等方面进行逐一分析来比较不同。 话不多话,看下…...

到底什么是股票委托接口?
在量化股票市场上,常见的股票委托接口其实有着不一样的交集,就拿股票交易接口,在量化股票跟程序化交易中,有共同之处就是在于直接委托执行下单,并且能很快的就能够将策略输出在账户持仓数据中,继续缓存下来…...

Linux驱动:VPU
1. 前言 限于作者能力水平,本文可能存在谬误,因此而给读者带来的损失,作者不做任何承诺。 2. 概述 VPU 是用来进行图像、视频数据进行硬件编、解码的硬件模块。内部集成了 Encoder、Decoder 功能部件进行图像、视频数据进行硬件编、解码&a…...
简介Servlet
目录 一、maven中心库 二、简介Servlet 三、实现Servlet动态页面 1、创建一个maven项目 2、引入依赖 3、创建目录结构 4、编写Servlet代码 5、打包 6、部署 7、验证程序 四、Servlet的运行原理 五、Tomcat伪代码 1、Tomcat初始化 a、让Tomcat先从指定的目录…...

Learning C++ No.7
引言: 北京时间:20223/2/9/22:20,距离大一下学期开学还有2天,昨天收到好消息,开学不要考试了,我并不是害怕考试,考试在我心里,地位不高,可能只有当我挂了,才能…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

JVM垃圾回收机制全解析
Java虚拟机(JVM)中的垃圾收集器(Garbage Collector,简称GC)是用于自动管理内存的机制。它负责识别和清除不再被程序使用的对象,从而释放内存空间,避免内存泄漏和内存溢出等问题。垃圾收集器在Ja…...

C# 类和继承(抽象类)
抽象类 抽象类是指设计为被继承的类。抽象类只能被用作其他类的基类。 不能创建抽象类的实例。抽象类使用abstract修饰符声明。 抽象类可以包含抽象成员或普通的非抽象成员。抽象类的成员可以是抽象成员和普通带 实现的成员的任意组合。抽象类自己可以派生自另一个抽象类。例…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

【OSG学习笔记】Day 16: 骨骼动画与蒙皮(osgAnimation)
骨骼动画基础 骨骼动画是 3D 计算机图形中常用的技术,它通过以下两个主要组件实现角色动画。 骨骼系统 (Skeleton):由层级结构的骨头组成,类似于人体骨骼蒙皮 (Mesh Skinning):将模型网格顶点绑定到骨骼上,使骨骼移动…...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...
