专题:曲面的切平面、法线
假设曲面方程为隐函数 F ( x , y , z ) = 0 ,点 M ( x 0 , y 0 , z 0 ) 是其上一点 又在点 M 处任意引一条在曲面上的曲线,设该曲线参数方程为: { x = φ ( t ) y = ψ ( t ) z = ω ( t ) ,且当 t = t 0 时, x = x 0 , y = y 0 , z = z 0 那么 F ( φ ( t ) , ψ ( t ) , ω ( t ) ) = 0 对 t 求全导,得 F x φ ′ ( t 0 ) + F y ψ ′ ( t 0 ) + F z ω ′ ( t 0 ) = 0 分析: 由于 ( φ ′ ( t 0 ) , ψ ′ ( t 0 ) , ω ′ ( t 0 ) ) 表达的是曲线的切向量, 因此上式表达的是向量 ( F x , F y , F z ) 与切向量垂直 而该曲线是经过点 M 的任意曲线, 如果一个向量与任意切线都垂直的话, 那这些任意切线必定在一个平面内, 这个平面就叫做曲面在点M处的切平面 而 ( F x , F y , F z ) 为 曲面在点M处的一个法向量 因此很容易得到切平面方程为: F x ( x − x 0 ) + F y ( y − y 0 ) + F z ( z − z 0 ) = 0 法线方程为: x − x 0 F x = y − y 0 F y = z − z 0 F z 如果曲面由显函数 z = f ( x , y ) 给出, 则 F ( x , y , z ) = f ( x , y ) − z = 0 , F x = f x , F y = f y , F z = − 1 法向量 ( F x , F y , F z ) 的模为 1 + f x 2 + f y 2 假设法向量朝 z 轴正向,则方向余弦为: cos α = − f x 1 + f x 2 + f y 2 , cos β = − f y 1 + f x 2 + f y 2 , cos γ = 1 1 + f x 2 + f y 2 假设曲面方程为隐函数F(x,y,z)=0,点M(x_0,y_0,z_0)是其上一点 \\ 又在点M处任意引一条在曲面上的曲线,设该曲线参数方程为:\\ \begin{cases} x=\varphi(t) \\ y=\psi(t) \\ z=\omega(t) \\ \end{cases},且当t=t_0时,x=x_0,y=y_0,z=z_0 \\ 那么F(\varphi(t),\psi(t),\omega(t)) = 0 \\ 对t求全导,得F_x\varphi^{\prime}(t_0)+F_y\psi^{\prime}(t_0)+F_z\omega^{\prime}(t_0)=0 \\ \,\\ 分析:\\ 由于(\varphi^{\prime}(t_0),\psi^{\prime}(t_0),\omega^{\prime}(t_0))表达的是曲线的切向量,\\ 因此上式表达的是向量(F_x,F_y,F_z)与切向量垂直\\ 而该曲线是经过点M的任意曲线,\\ 如果一个向量与任意切线都垂直的话,\\ 那这些任意切线必定在一个平面内,\\ \textbf{这个平面就叫做曲面在点M处的切平面} \\ 而(F_x,F_y,F_z)为\textbf{曲面在点M处的一个法向量} \\ 因此很容易得到切平面方程为:\\ F_x(x-x_0)+F_y(y-y_0)+F_z(z-z_0)=0 \\ 法线方程为:\\ \frac{x-x_0}{F_x}=\frac{y-y_0}{F_y}=\frac{z-z_0}{F_z} \\ \,\\ 如果曲面由显函数z=f(x,y)给出,\\ 则F(x,y,z)=f(x,y)-z=0,F_x=f_x,F_y=f_y,F_z=-1 \\ 法向量(F_x,F_y,F_z)的模为\sqrt{1+f_x^2+f_y^2} \\ 假设法向量朝z轴正向,则方向余弦为:\\ \cos\alpha=\frac{-f_x}{\sqrt{1+f_x^2+f_y^2}},\cos\beta=\frac{-f_y}{\sqrt{1+f_x^2+f_y^2}},\cos\gamma=\frac{1}{\sqrt{1+f_x^2+f_y^2}} 假设曲面方程为隐函数F(x,y,z)=0,点M(x0,y0,z0)是其上一点又在点M处任意引一条在曲面上的曲线,设该曲线参数方程为:⎩ ⎨ ⎧x=φ(t)y=ψ(t)z=ω(t),且当t=t0时,x=x0,y=y0,z=z0那么F(φ(t),ψ(t),ω(t))=0对t求全导,得Fxφ′(t0)+Fyψ′(t0)+Fzω′(t0)=0分析:由于(φ′(t0),ψ′(t0),ω′(t0))表达的是曲线的切向量,因此上式表达的是向量(Fx,Fy,Fz)与切向量垂直而该曲线是经过点M的任意曲线,如果一个向量与任意切线都垂直的话,那这些任意切线必定在一个平面内,这个平面就叫做曲面在点M处的切平面而(Fx,Fy,Fz)为曲面在点M处的一个法向量因此很容易得到切平面方程为:Fx(x−x0)+Fy(y−y0)+Fz(z−z0)=0法线方程为:Fxx−x0=Fyy−y0=Fzz−z0如果曲面由显函数z=f(x,y)给出,则F(x,y,z)=f(x,y)−z=0,Fx=fx,Fy=fy,Fz=−1法向量(Fx,Fy,Fz)的模为1+fx2+fy2假设法向量朝z轴正向,则方向余弦为:cosα=1+fx2+fy2−fx,cosβ=1+fx2+fy2−fy,cosγ=1+fx2+fy21
相关文章:

专题:曲面的切平面、法线
假设曲面方程为隐函数 F ( x , y , z ) 0 ,点 M ( x 0 , y 0 , z 0 ) 是其上一点 又在点 M 处任意引一条在曲面上的曲线,设该曲线参数方程为: { x φ ( t ) y ψ ( t ) z ω ( t ) ,且当 t t 0 时, x x 0 , y y…...
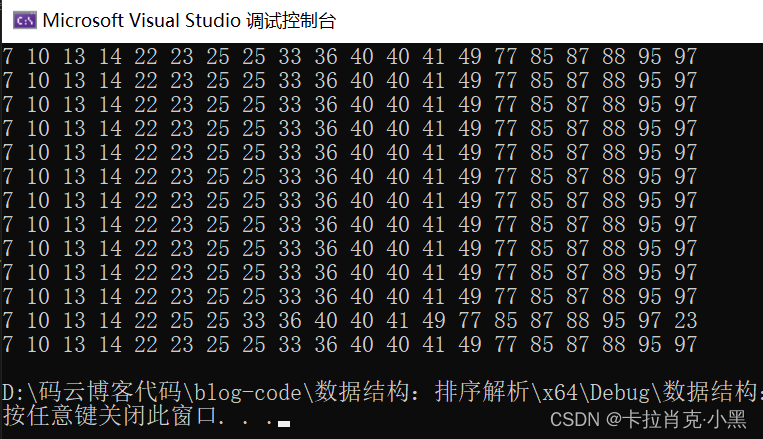
数据结构:排序解析
文章目录 前言一、常见排序算法的实现1.插入排序1.直接插入排序2.希尔排序 2.交换排序1.冒泡排序2.快速排序1.hoare版2.挖坑版3.前后指针版4.改进版5.非递归版 3.选择排序1.直接选择排序2.堆排序 4.归并排序1.归并排序递归实现2.归并排序非递归实现 5.计数排序 二、排序算法复杂…...
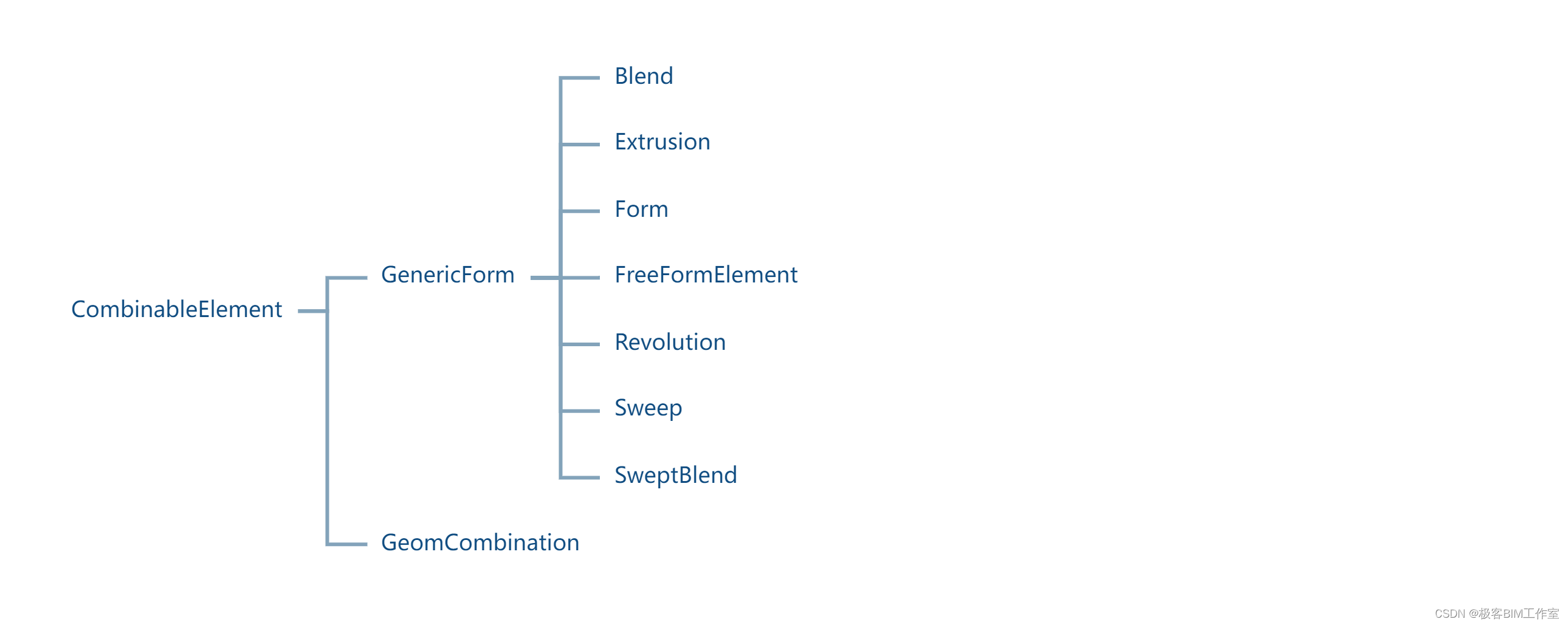
Revit SDK:AutoJoin 自动合并体量
前言 Revit 有一套完整的几何造型能力,每一个体量都是一个GenericForm,这些体量可以通过拉伸、扫掠等创建。这个例子介绍如何将他们合并成一个体量。 内容 合并体量的关键接口: // Autodesk.Revit.DB.Document public GeomCombination Com…...
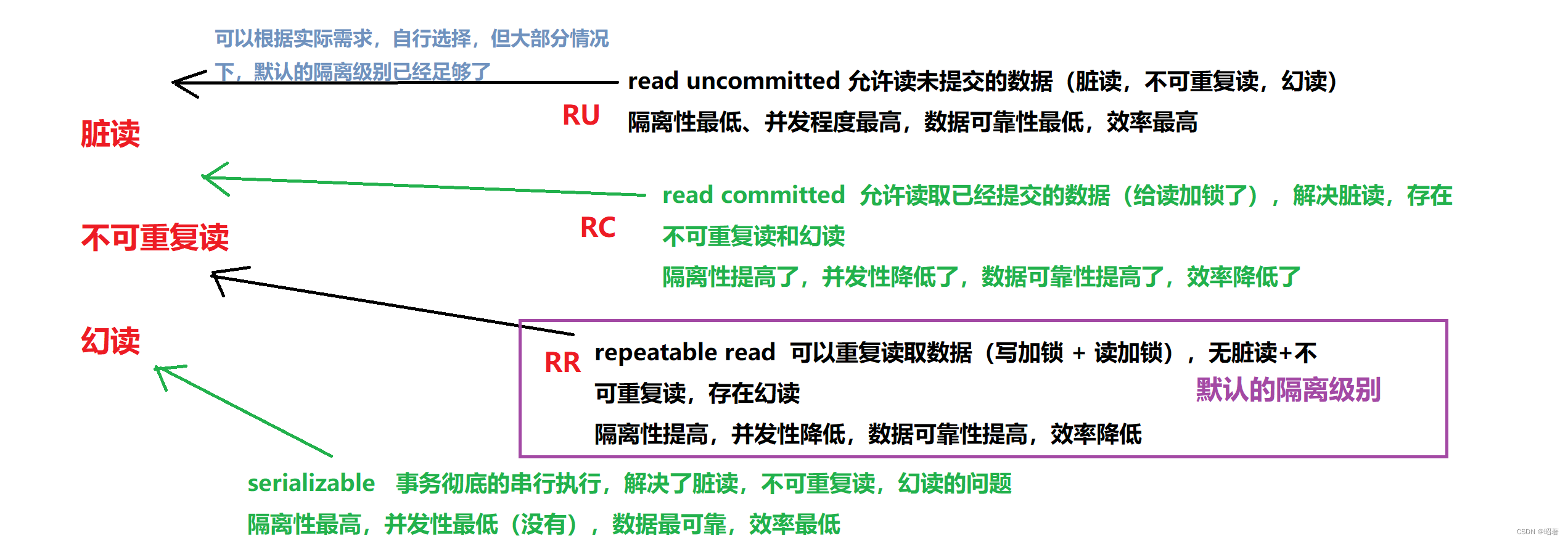
MYSQL(索引、事务)
文章目录 一、索引二、事务 一、索引 数据库中的表、数据、索引之间的关系,类似于书架上的图书、书籍内容和书籍目录的关系 1. 概述 概念:相当于是一本书的目录,是以‘列’为维度进行建立的使用场景:如果我们要查询一个表中的某个…...
设置Docker容器内的中文字符集,解决某些情况下中文乱码的问题)
部署问题集合(二十三)设置Docker容器内的中文字符集,解决某些情况下中文乱码的问题
前言: 同事给了一个服务,在Windows环境下怎么跑都正常,但一到Linux虚拟机里就中文乱码起初就想到了可能是字符集的问题,但调整了半天也没见效果,最后隔了几天突然想到,我是构建Docker跑的,而且…...

Web AP—PC端网页特效
PC端网页特效 代码下载 元素偏移量 offset 系列 offset 翻译过来就是偏移量, 我们使用 offset系列相关属性可以动态的得到该元素的位置(偏移)、大小等。 获得元素距离带有定位父元素的位置获得元素自身的大小(宽度高度&#x…...

Spring线程池ThreadPoolTaskExecutor使用
为什么使用线程池? 降低系统资源消耗,通过重用已存在的线程,降低线程创建和销毁造成的消耗;提高系统响应速度,当有任务到达时,通过复用已存在的线程,无需等待新线程的创建便能立即执行…...

spring mvc的执行流程
请求拦截。用户发起请求,请求先被sevlet拦截,转发给spring mvc框架请求转发。spring mvc里面的DispcherServlet会接收到请求并转发给HandlerMapping匹配接口。HandlerMapping负责解析请求,根据请求信息和配置信息找到匹配的controller类&…...
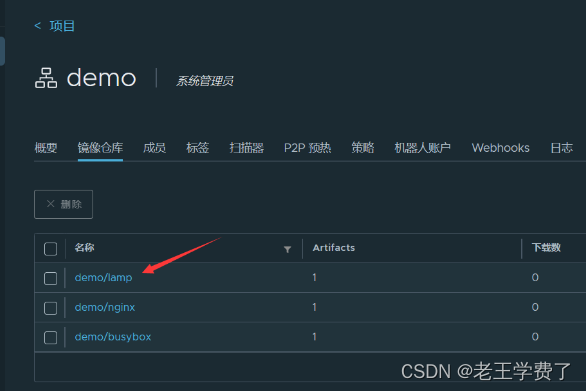
docker作业
目录 1、使用mysql:5.6和 owncloud 镜像,构建一个个人网盘。 1.1启动镜像 1.2启动cloud镜像 1.3浏览器访问 编辑 2、安装搭建私有仓库 Harbor 2.1下载docker-compose 2.2 磁盘挂载,保存harbor 2.3 修改配置文件 2.4安装 2.5浏览器访问 2.6 新…...

java实现本地文件转文件流发送到前端
java实现本地文件转文件流发送到前端 Controller public void export(HttpServletResponse response) {// 创建file对象response.setContentType("application/octet-stream");// 文件名为 sresponse.setHeader("Content-Disposition", "attachment;…...
2020ICPC南京站
K K Co-prime Permutation 题意:给定n和k,让你构造n的排列,满足gcd(pi, i)1的个数为k。 思路:因为x和x-1互质,1和任何数互质,任何数和它本身不互质 当k为奇数时,p11,后面k-1个数…...

Linux 中的 chsh 命令及示例
介绍 bash shell 是 Linux 最流行的登录 shell 之一。但是,对于不同的命令行操作,可以使用替代方法。chshLinux 中的( change shell )命令使用户能够修改登录 shell 。 以下教程...

JavaScript 数组如何实现冒泡排序?
冒泡排序是一种简单但效率较低的排序算法,常用于对小型数据集进行排序。它的原理是多次遍历数组,比较相邻元素的大小,并根据需要交换它们的位置,将最大(或最小)的元素逐渐“冒泡”到数组的一端。这个过程会…...

ZooKeeper集群环境搭建
🥇🥇【大数据学习记录篇】-持续更新中~🥇🥇 个人主页:beixi 本文章收录于专栏(点击传送):【大数据学习】 💓💓持续更新中,感谢各位前辈朋友们支持…...
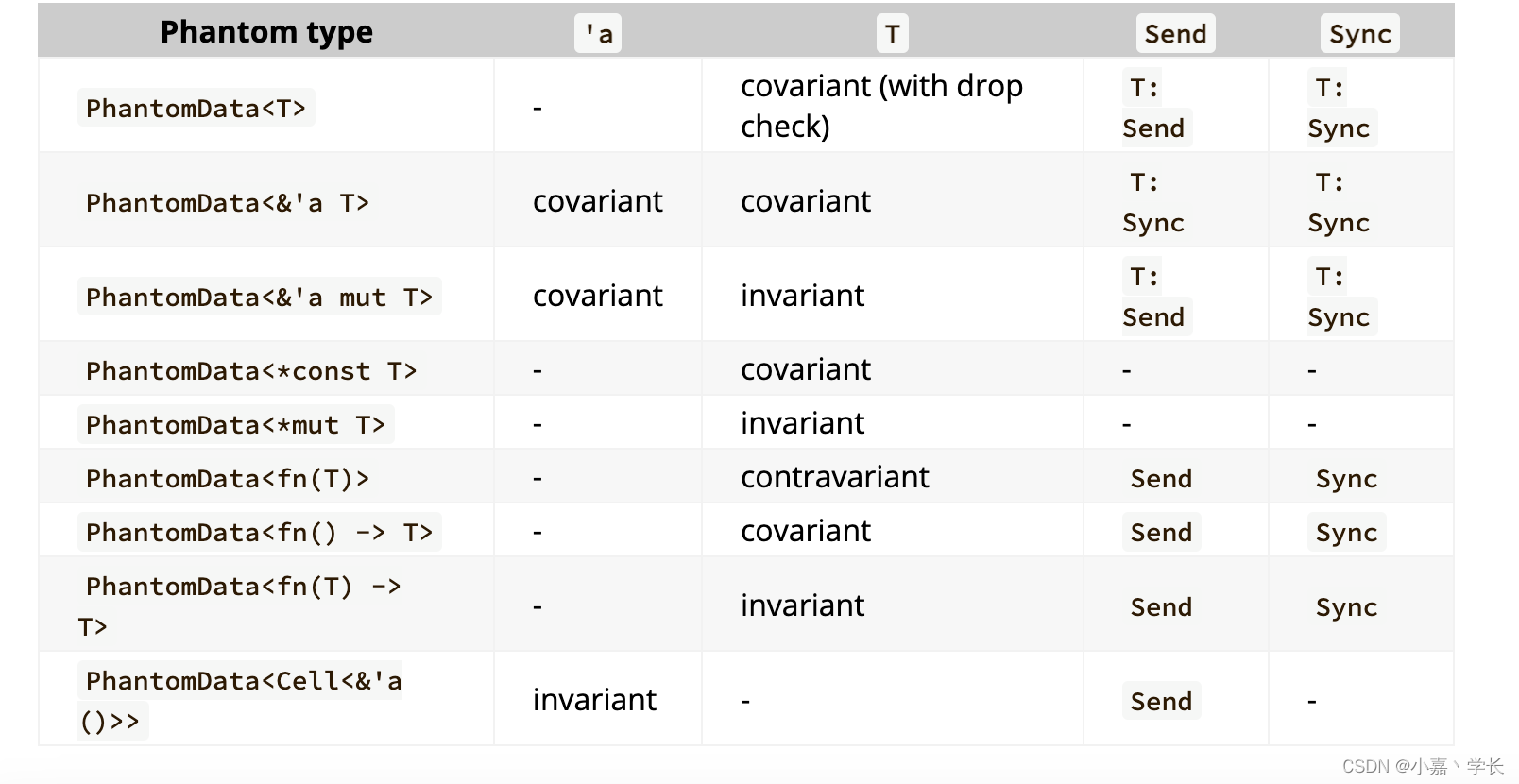
【跟小嘉学 Rust 编程】二十、进阶扩展
系列文章目录 【跟小嘉学 Rust 编程】一、Rust 编程基础 【跟小嘉学 Rust 编程】二、Rust 包管理工具使用 【跟小嘉学 Rust 编程】三、Rust 的基本程序概念 【跟小嘉学 Rust 编程】四、理解 Rust 的所有权概念 【跟小嘉学 Rust 编程】五、使用结构体关联结构化数据 【跟小嘉学…...

pytorch学习过程中一些基础语法
1、tensor.view()函数,通俗理解就是reshape,#参数这里的-1需要注意,可以根据原张量size自行计算 data1torch.randn((4,2)) data2data1.view(2,4) data3data2.view(-1,8)2、tensor.max()函数,在分类问题中,通常需要使用…...

判断聚类 n_clusters
目录 基本原理 代码实现: 肘部法则(Elbow Method): 轮廓系数(Silhouette Coefficient) Gap Statistic(间隙统计量): Calinski-Harabasz Index(Calinski-…...

基于深度学习的网络异常检测方法研究
摘要: 本文提出了一种基于深度学习的网络异常检测方法,旨在有效地识别网络中潜在的异常行为。通过利用深度学习算法,结合大规模网络流量数据的训练,我们实现了对复杂网络环境下的异常行为的准确检测与分类。实验结果表明…...
SSM 基于注解的整合实现
一、pom.xml <project xmlns"http://maven.apache.org/POM/4.0.0" xmlns:xsi"http://www.w3.org/2001/XMLSchema-instance"xsi:schemaLocation"http://maven.apache.org/POM/4.0.0 http://maven.apache.org/maven-v4_0_0.xsd"><modelV…...

工具类APP如何解决黏性差、停留短、打开率低等痛点?
工具产品除了需要把自己的功能做到极致之外,其实需要借助一些情感手段、增设一些游戏机制、输出高质量内容、搭建社区组建用户关系链等方式,来提高产品的用户黏性,衍生产品的价值链。 工具类产品由于进入门槛低,竞争尤为激烈&…...

龙虎榜——20250610
上证指数放量收阴线,个股多数下跌,盘中受消息影响大幅波动。 深证指数放量收阴线形成顶分型,指数短线有调整的需求,大概需要一两天。 2025年6月10日龙虎榜行业方向分析 1. 金融科技 代表标的:御银股份、雄帝科技 驱动…...

通过Wrangler CLI在worker中创建数据库和表
官方使用文档:Getting started Cloudflare D1 docs 创建数据库 在命令行中执行完成之后,会在本地和远程创建数据库: npx wranglerlatest d1 create prod-d1-tutorial 在cf中就可以看到数据库: 现在,您的Cloudfla…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...

Java 二维码
Java 二维码 **技术:**谷歌 ZXing 实现 首先添加依赖 <!-- 二维码依赖 --><dependency><groupId>com.google.zxing</groupId><artifactId>core</artifactId><version>3.5.1</version></dependency><de…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...
