小米面试题——不用加减乘除计算两数之和
前言
(1)刷B站看到一个面试题,不用加减乘除计算两数之和。
(2)当时我看到这个题目,第一反应就是感觉这是一个数电题目。不过需要采用C语言的方式编写出来。
(3)不过看到大佬的代码之后,感觉自己的思想还是太局限了。
利用数电知识解题
(1)当时我看到这个题目,第一想法就是画出逻辑电路图,分析过程我就不赘述了。感兴趣的可以看【硬件科普】带你认识CPU第02期——CPU是怎么计算加法的(上)这个视频讲解
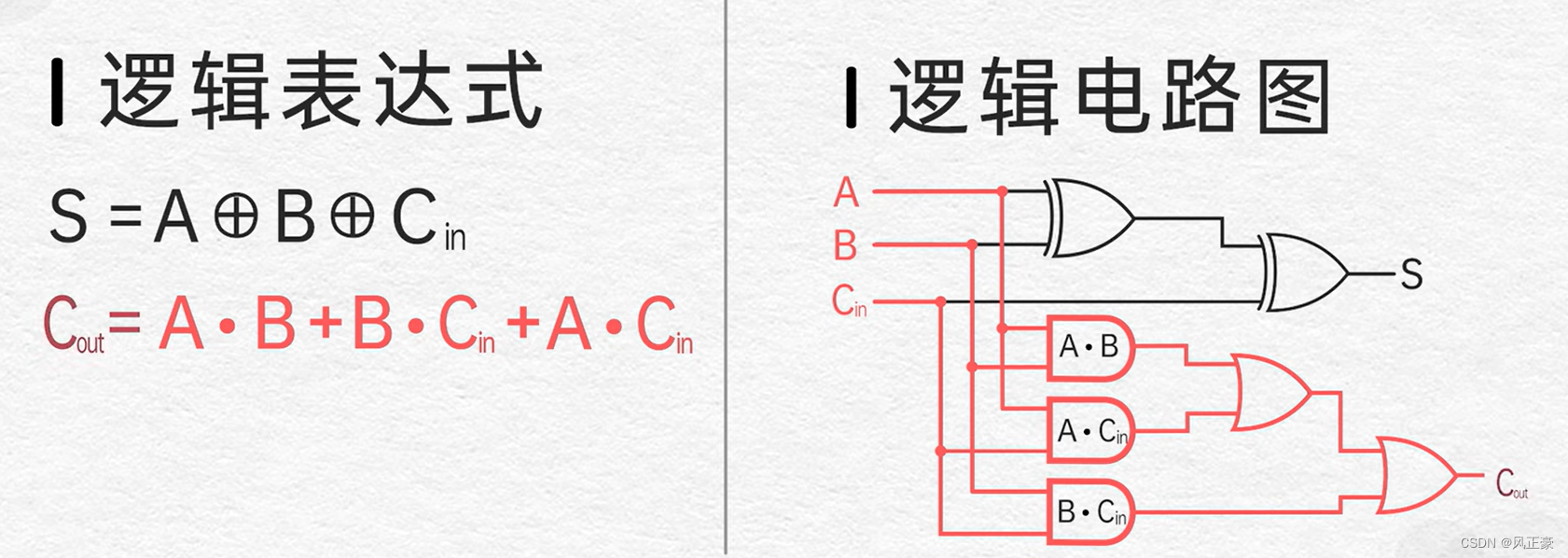
(2)根据上图,于是我们可以知道,需要一个当前值a和b,一个输入的进位值carry_bit。最终输出数据S和进位符号carry_bit。
注意:carry_bit是进位符号,所以他每次计算的时候,需要左移1位,否则他就是在上一位,最终输出的是一个错误数据。
#define get_bit(data,bit) (data & (0x01 << bit))
#define AND(a,b,i) (get_bit(a,i) & get_bit(b,i))
int ADD(int a,int b)
{int i,carry_bit=0,ret=0;for(i=0 ; i<16 ; i++){ret |= get_bit(a,i) ^ get_bit(b,i) ^ (carry_bit<<1); //计算本位值carry_bit = AND(a,b,i) | AND(a,carry_bit,i) | (get_bit(b,i) & (carry_bit<<1)); //计算进位值}return ret;
}
将上面代码精简
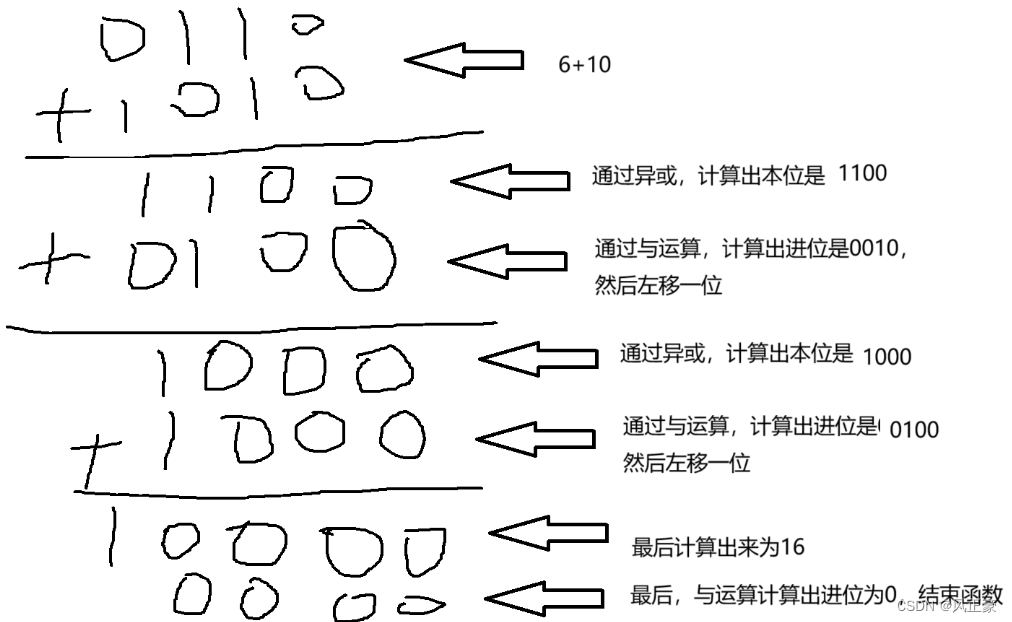
(1)这个是一个大佬的思路,与我们上面一样,建立一个本位和一个进位。不过这一次与上一次不一样的点在于,上一次每次都是一位一位的进行操作。而大佬是直接将本位的值利用异或运算一次性计算出来,进位值利用与运算保留。
(2)得到进位值之和,将进位制左移一位,再与上一次的本位进行异或运算,得到进位制。循环往复,最终直到进位制消失。
int ADD(int x,int y)
{while(y != 0) //直到进位值消失{int tmp = x^y; //异或,计算出本位y = (x&y)<<1; //与,计算出进位x = tmp;}
}
相关文章:

小米面试题——不用加减乘除计算两数之和
前言 (1)刷B站看到一个面试题,不用加减乘除计算两数之和。 (2)当时我看到这个题目,第一反应就是感觉这是一个数电题目。不过需要采用C语言的方式编写出来。 (3)不过看到大佬的代码之…...

Mysql 日志管理 数据备份
MySQL日志管理 MySQL的默认日志保存位置为/usr/local/mysql/data 日志开启方式有两种:通过配置文件或者是通过命令 通过命令修改开启的日志是临时的,关闭或重启服务后就会关闭 日志的分类 1.错误日志 用来记录当MySQL启动、停止或运行时发生的错误信…...

Java小记-腾讯2020校招-后台-逛街
题目描述: 小Q在周末的时候和他的小伙伴来到大城市逛街,一条步行街上有很多高楼,共有n座高楼排成一行。 小Q从第一栋一直走到了最后一栋,小Q从来都没有见到这么多的楼,所以他想知道他在每栋楼的位置处能看到多少栋楼呢…...
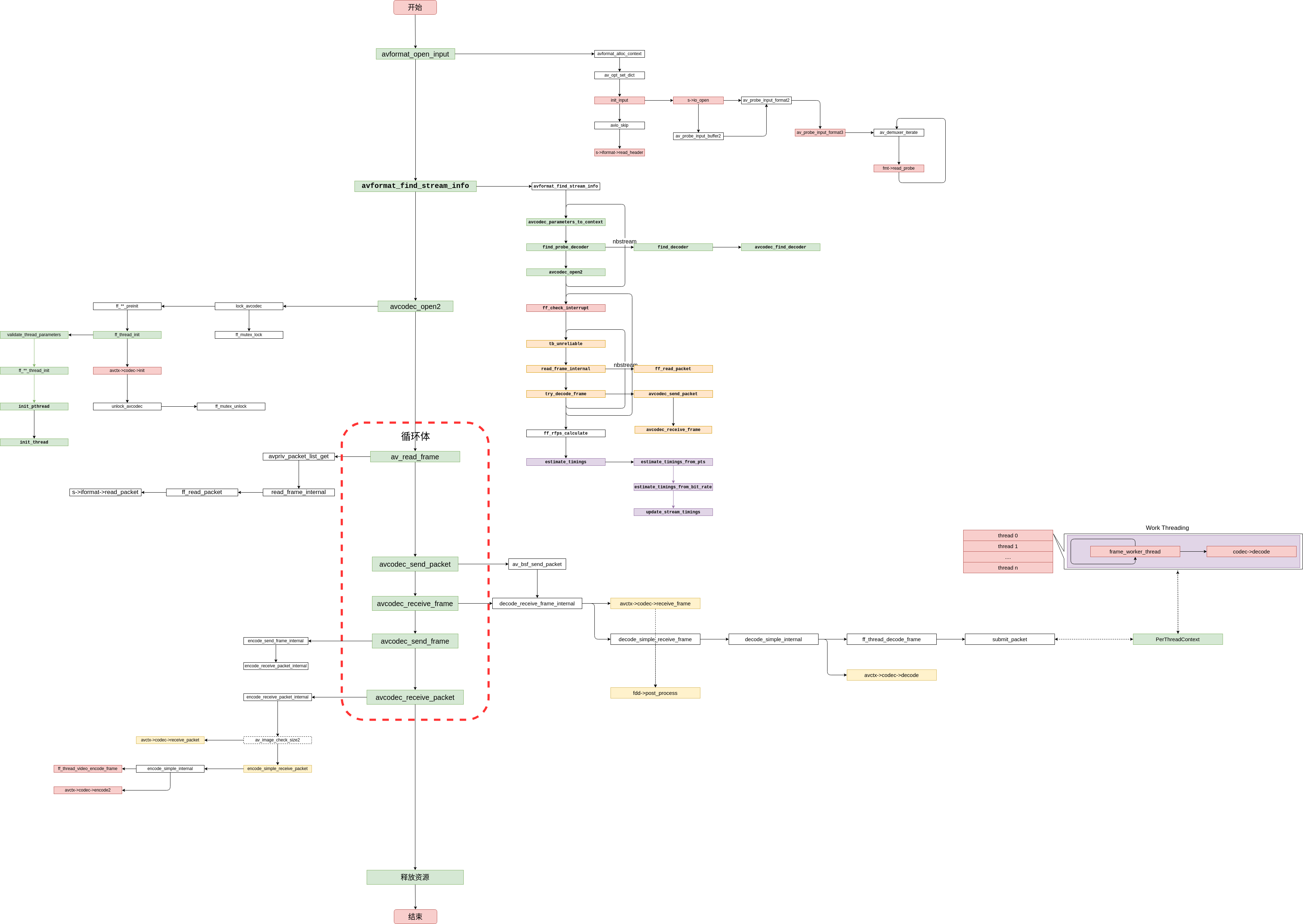
FFmpeg5.0源码阅读——FFmpeg大体框架
摘要:前一段时间熟悉了下FFmpeg主流程源码实现,对FFmpeg的整体框架有了个大概的认识,因此在此做一个笔记,希望以比较容易理解的文字描述FFmpeg本身的结构,加深对FFmpeg的框架进行梳理加深理解,如果文章中有…...

【算法刷题之字符串篇】
目录 1.leetcode-344. 反转字符串(1)方法:双指针 2.leetcode-541. 反转字符串 II(1)方法一:模拟(2)方法二:双指针 3.leetcode-剑指 Offer 05. 替换空格(1&…...

js中forEach和map的区别:forEach不会改变原数组,而map会改变数组?错了错了
1.提出思考?forEach不会改变原数组,而map会改变数组? 看到掘金上一篇文章觉得很有意思:大致是描述一般面试官问js中forEach和map的区别?都会回答forEach不会改变原数组,而map会改变,我也一直对…...

深度对话:从底层看Sui设计理念及网络规模扩展
近日,我们采访了George Danezis以了解Sui的交易处理系统如何促成高性能网络。他是Mysten Labs的联合创始人和首席科学家(Sui的最初贡献者),也是伦敦大学学院(University College London,UCL)安全…...

2.单链表练习
1. 链表的基本概念 链表(Linked List)是一种常见的数据结构,用于存储一系列元素,这些元素可以是任意类型的数据。链表中的每个元素被称为节点(Node),每个节点包含两部分:一个存储数…...

Wordpress 安装插件和主题报错
安装主题和插件的时候,就是这个恶心的报错, Wordpress plugin install: Could not create directory 这是权限惹的祸,如下一顿操作猛如虎,就解决了。 sudo chown -R www:www wp-content/themes sudo chown -R www:www wp-conte…...
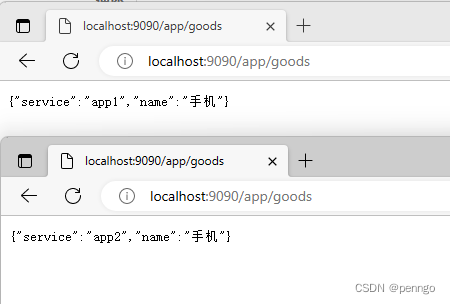
Spring Cloud 2022.x版本使用gateway和nacos实现动态路由和负载均衡
文章目录 1、nacos下载安装1.1、启动服务器1.2、关闭服务器1.3、服务注册&发现和配置管理接口 2、代码示例2.1、app1工程代码2.2、app2工程代码2.3、gateway网关工程代码 3、动态配置网关路由3.1、配置动态路由3.2、配置为负载模式 4、gateway配置规则4.1、请求转发&#x…...

CSS中如何隐藏元素但保留其占位空间(display:none vs visibility:hidden)?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ display: none;⭐ visibility: hidden;⭐ 如何选择⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带你启航前端之旅 欢迎来到前端入门之旅!这个专栏是为…...

无涯教程-机器学习 - 数据可视化
在上一章中,无涯教程讨论了数据对于机器学习算法的重要性,以了解具有统计信息的数据,还有另一种称为可视化的方式来理解数据。 借助数据可视化,可以看到数据的属性保持什么样的关联,这是查看要素是否与输出相对应的最…...

springboot设置日志输出级别
一、日志等级 trace:最低等级 debug:调试用,通常用于跟踪程序进展 info: 记录用,通常用于记录程序行为 warn:警告 error:错误 fatal:灾难性错误,最高等级 配置application.yml 实现…...
buildAdmin的使用笔记
安装buildAdmin 下载完整包,解压进入 buildadmin 的文件夹, 输入命令 composer install 启动的时候使用, php think run 就可以了 为什么启动只需要, php think run 这种启动方式, 我是头一回看见 ,后来才…...
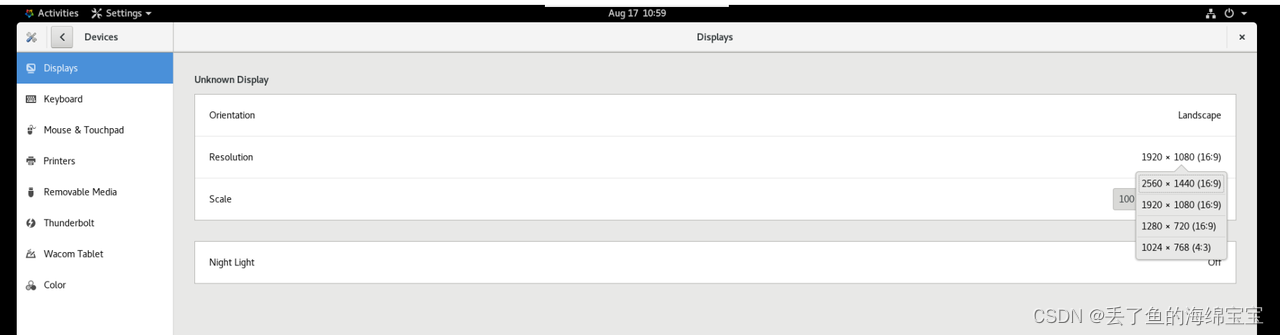
RealVNC配置自定义分辨率(AlmaLinux 8)
RealVNC 配置自定义分辨率(AlmaLinux8) 参考RealVNC官网 how to set up resolution https://help.realvnc.com/hc/en-us/articles/360016058212-How-do-I-adjust-the-screen-resolution-of-a-virtual-desktop-under-Linux-#standard-dummy-driver-0-2 …...

LA@特征值和特征向量的性质
文章目录 方阵特征值和特征向量的性质👺特征值之和特征值之积推论:特征值判定方阵的可逆性 证明小结 导出性质可逆矩阵的特征值性质转置矩阵和特征值矩阵多项式的特征值不同特征值的特征向量线性无关定理推论推广 特征向量线性组合特征值的重数性质 方阵特征值和特征…...

Springboot使用kafka事务-生产者方
前言 在上一篇文章中,我们使用了springboot的AOP功能实现了kafka的分布式事务,但是那样实现的kafka事务是不完美的,因为请求进来之后分配的是不同线程,但不同线程使用的kafka事务却是同一个,这样会造成多请求情况下的…...

您的计算机已被.halo勒索病毒感染?恢复您的数据的方法在这里!
导言: 在当今数字时代,网络安全已经成为了我们生活和工作中不可或缺的一部分。然而, .Halo 勒索病毒的出现,使网络威胁变得更加真切和具体。本文91数据恢复将深入介绍 .Halo 勒索病毒的危害,详细探讨如何高效地恢复被其…...

生成式AI颠覆传统数据库的十种方式
对于生成式AI的所有闪光点,这个新时代最大的转变可能深埋在软件堆栈中。AI算法正在不易觉察地改变一个又一个数据库。他们正在用复杂、自适应且看似更直观的AI新功能颠覆传统数据库。 与此同时,数据库制造商正在改变我们存储信息的方式,以便…...
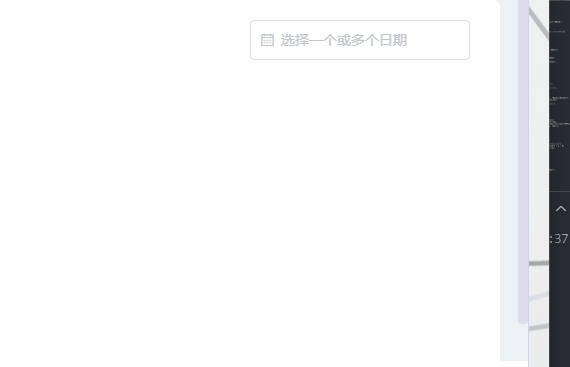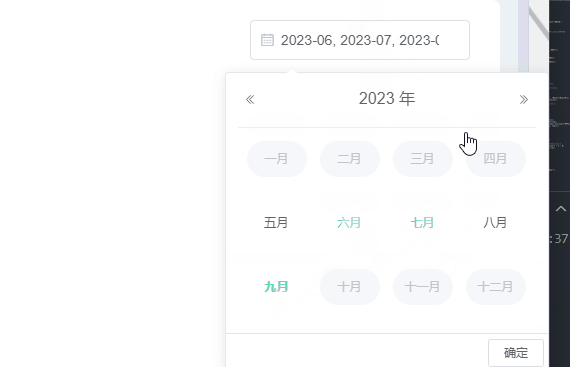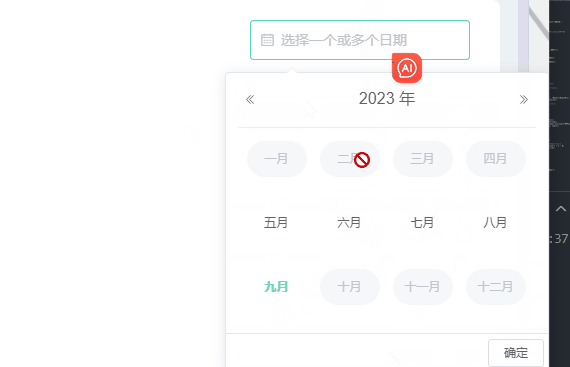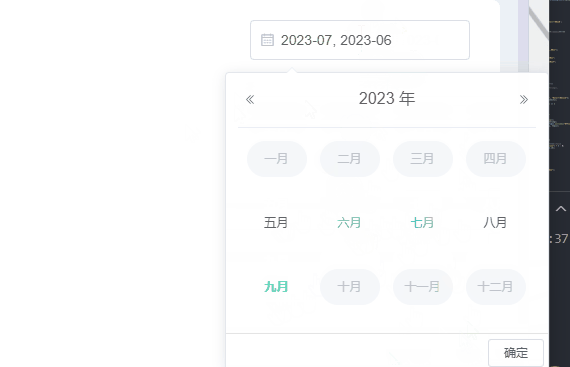
el-date-picker自定义只能选中当前月份和半年内月份等
需求:el-date-picker只能选中当前月期和当前月期往前半年,其他时间就禁用了不让选择了,因为没数据哈哈。当然也可以选择往前一年等。 一、效果 二、写个日期选择器 :picker-options:日期选项 value-format:选择后的格…...

利用最小二乘法找圆心和半径
#include <iostream> #include <vector> #include <cmath> #include <Eigen/Dense> // 需安装Eigen库用于矩阵运算 // 定义点结构 struct Point { double x, y; Point(double x_, double y_) : x(x_), y(y_) {} }; // 最小二乘法求圆心和半径 …...
:にする)
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする
日语学习-日语知识点小记-构建基础-JLPT-N4阶段(33):にする 1、前言(1)情况说明(2)工程师的信仰2、知识点(1) にする1,接续:名词+にする2,接续:疑问词+にする3,(A)は(B)にする。(2)復習:(1)复习句子(2)ために & ように(3)そう(4)にする3、…...

盘古信息PCB行业解决方案:以全域场景重构,激活智造新未来
一、破局:PCB行业的时代之问 在数字经济蓬勃发展的浪潮中,PCB(印制电路板)作为 “电子产品之母”,其重要性愈发凸显。随着 5G、人工智能等新兴技术的加速渗透,PCB行业面临着前所未有的挑战与机遇。产品迭代…...

JavaScript 中的 ES|QL:利用 Apache Arrow 工具
作者:来自 Elastic Jeffrey Rengifo 学习如何将 ES|QL 与 JavaScript 的 Apache Arrow 客户端工具一起使用。 想获得 Elastic 认证吗?了解下一期 Elasticsearch Engineer 培训的时间吧! Elasticsearch 拥有众多新功能,助你为自己…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

【无标题】湖北理元理律师事务所:债务优化中的生活保障与法律平衡之道
文/法律实务观察组 在债务重组领域,专业机构的核心价值不仅在于减轻债务数字,更在于帮助债务人在履行义务的同时维持基本生活尊严。湖北理元理律师事务所的服务实践表明,合法债务优化需同步实现三重平衡: 法律刚性(债…...
