C++算法 —— 分治(1)快排
文章目录
- 1、颜色分类
- 2、排序数组
- 3、第k个最大的元素(快速选择)
- 4、最小的k个数(快速选择)
分治,就是分而治之,把大问题划分成多个小问题,小问题再划分成更小的问题。像快排和归并排序就是分治思想。分治需要把数据分成几个区间,分区间则要通过基准值来划分
1、颜色分类
颜色分类

其实这道题的做法是三指针。双指针思路中,定义两个指针,假设要把整个数组划分成a和b区间,ab区间的数有各自的特点,一个指针遍历整个数组,另一个指针指向a区间的最后一个元素位置。而三指针,也是同样的思路,三个指针,abc三个区间,一个指针仍然在遍历数组,但它不需要遍历完所有,一个指针指向a区间的最右侧,一个指针指向c区间的最左侧,这样三个区间也就能划分出来了。在实际操作中,会分出四个区间
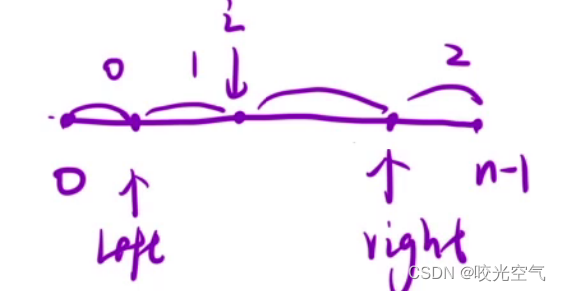
[0, left]全是0,[left + 1, i - 1]全是1,[i, right - 1]是待扫描的元素,[right, n - 1]全是2。
代码开始时,我们要如何做?left和right自然是在整个数组下标的0和n - 1处,i每次检测到数字,就去判断应该放到哪个区间,然后交换元素,把数字放到区间,left或者right移动,而i如果是放到left左边,i可以++,但是和right右边的元素交换后,i不能++,它还需要判断交换过来的数字。
void sortColors(vector<int>& nums) {int n = nums.size();int i = 0, left = -1, right = n;//为什么要这么设置left和right1的值? 看下面的代码就能明白了while(i < right)//为什么要小于right?right到最后都是为2的元素,等到i和right重合时,其实就已经完成了整体的排序{if(nums[i] == 0){swap(nums[++left], nums[i++]);}else if(nums[i] == 1){i++;}else if(nums[i] == 2){swap(nums[--right], nums[i]);}}}
2、排序数组
排序数组

其实这道题就是实现快排。我们要设置基准值key,把区间划分成两部分,<=key 和 >key,然后再到两个区间实现同样的操作,找key,划分区间。如果数组里都是重复元素的话,这个排序的复杂度就不好了。那么这里就把数组分三块的思想来实现快排,其实这个数组分三块的思路就是排序(2)那篇博客中的双指针法,思路都相似。我们要分成三个区间,< key = key > key,每次比较的时候就是交换,指针++等操作。
同上面一样
小于key:swap(nums[++left], nums[i++])
等于key:i++
大于key:swap(nus[–right], nums[i])
但是这里还有优化,上面时间复杂度是O(N),想要达成N * logN,就必须要随机选取key值。而这里的随机也不是简单的随机,我们要让整个区间的数都能等概率地没取到,我们的做法就是rand() % (right - left + 1) + left,偏移量 + left得到对应的数值,这个得出来的值是数组的下标,也就是nums[rand() % (right - left + 1) + left]。
上代码
vector<int> sortArray(vector<int>& nums) {srand(time(NULL));//开始随机,种下随机数种子qsort(nums, 0, nums.size() - 1);return nums;}void qsort(vector<int>& nums, int l, int r){if(l >= r) return ;//数组分三块int key = getRandom(nums, l, r);int i = l, left = l - 1, right = r + 1;//这里就和上面的颜色分类的做法就一样了,也就是上面灰框中的实现while(i < right){if(nums[i] < key) swap(nums[++left], nums[i++]);else if(nums[i] == key) i++;else swap(nums[--right], nums[i]);}qsort(nums, l, left);qsort(nums, right, r);}int getRandom(vector<int>& nums, int left, int right){int r = rand();return nums[r % (right - left + 1) + left];}
3、第k个最大的元素(快速选择)
数组中的第K个最大元素

TOP K有4种问题,第k大,第k小,前k大,前k小。之前的博客对此用的是堆排序的算法。还有另外一个就是快速选择算法。堆排是O(N*logN),而快速选择是O(N)。
快速选择基于快排。整个区间左右端点为l和r,分成三个区间abc,三个区间内,我们需要确定第k大的数字在哪个区间内。假设abc就是每个区间的元素个数,如果在第三个区间,也就是>key的区间,那么c >=k;如果第一个条件不成立,那么如果在第二区间,那么b + c >=k,直接返回key就行,因为第二个区间都是=key的数字;如果上面两个条件都不成立,那么就去第一个区间找,找k - (b + c)大的数字。
int findKthLargest(vector<int>& nums, int k) {/*priority_queue<int, vector<int>, greater<int>> pq(nums.begin(), nums.begin() + k);for(size_t i = k; i < nums.size(); ++i){if(nums[i] > pq.top()){pq.pop();pq.push(nums[i]);}}return pq.top();*///上面是用优先级队列解决的srand(time(NULL));return qsort(nums, 0, nums.size() - 1, k);}int qsort(vector<int>& nums, int l, int r, int k){if(l == r) return nums[l];//必然存在至少一个元素,所以l不可能大于r//1. 随机选择基准元素int key = getRandom(nums, l, r);//2. 根据基准元素分三块int left = l - 1, right = r + 1, i = l;while(i < right){if(nums[i] < key) swap(nums[++left], nums[i++]);else if(nums[i] == key) i++;else swap(nums[--right], nums[i]);}int c = r - right + 1;int b = right - left - 1;if(c >= k) return qsort(nums, right, r, k);else if(b + c >= k) return key;else return qsort(nums, l, left, k - b - c);}int getRandom(vector<int>& nums, int left, int right){return [rand() % (right - left + 1) + left];}
4、最小的k个数(快速选择)
剑指 Offer 40. 最小的k个数

针对这样的问题,我们可以堆排序,也可以快速选择算法。堆排是N * logk,快速选择可以到达N。
还是l ,left, right, r,abc。如果a > k,那就在a区间找;条件不符合,那就去a + b >= k,那就返回key,因为第一个条件不符合,那么第二个条件符合的话,k一定就是在=key的区间,那就返回key;上述两种条件都不符合,那就得在c区间找。
对上一个稍作修改。
vector<int> getLeastNumbers(vector<int>& arr, int k) {srand(time(NULL));qsort(arr, 0, arr.size() - 1, k);return {arr.begin(), arr.begin() + k};}void qsort(vector<int>& nums, int l, int r, int k){if(l == r) return ;int key = getRandom(nums, l, r);int left = l - 1, right = r + 1, i = l;while(i < right){if(nums[i] < key) swap(nums[++left], nums[i++]);else if(nums[i] == key) i++;else swap(nums[--right], nums[i]);}int a = left - l + 1;int b = right - left - 1;if(a > k) return qsort(nums, l, left, k);else if(b + a >= k) return ;else qsort(nums, right, r, k - b - a);}int getRandom(vector<int>& nums, int left, int right){return nums[rand() % (right - left + 1) + left];}
结束。
相关文章:

C++算法 —— 分治(1)快排
文章目录 1、颜色分类2、排序数组3、第k个最大的元素(快速选择)4、最小的k个数(快速选择) 分治,就是分而治之,把大问题划分成多个小问题,小问题再划分成更小的问题。像快排和归并排序就是分治思…...

接口用例设计
章节目录: 一、针对输入设计1.1 数值型1.2 字符串型1.3 数组或链表类型 二、针对业务逻辑2.1 约束条件分析2.2 操作对象分析2.3 状态转换分析2.4 时序分析 三、针对输出设计3.1 针对输出结果3.2 接口超时 四 、其他测试设计4.1 已废弃接口测试4.2 接口设计合理性分析…...

Selenium超级详细的教程
Selenium是一个用于自动化测试的工具,它可以模拟用户在浏览器中的各种操作。除了用于测试,Selenium还可以用于爬虫,特别是在处理动态加载页面时非常有用。本文将为您提供一个超级详细的Selenium教程,以帮助您快速入门并了解其各种…...
服务报network error错误
问题:服务请求时会偶发性的报【network error网络超时】(请求瞬间就报) 可能原因: 服务器linux内核调优时将:net.ipv4.tcp_tw_recycle设置为1,开启TCP连接中TIME-WAIT sockets的快速回收,默认为…...

【ES6】利用 Proxy实现函数名链式效果
利用 Proxy,可以将读取属性的操作(get),转变为执行某个函数,从而实现属性的链式操作。 var pipe function (value) {var funcStack [];var oproxy new Proxy({} , {get : function (pipeObject, fnName) {if (fnNa…...
hive部署
下载hive安装包:https://dlcdn.apache.org/hive/hive-2.3.9/解压及环境部署 tar -zxvf apache-hive-2.3.9-bin.tar.gz mv apache-hive-2.3.9-bin hivevim /etc/profile添加至环境变量 export HIVE_HOME/usr/local/hive export PATH$PATH:$HIVE_HOME/binsource /etc…...

ip白名单之网段
代码托管,有时候为了安全性,限制网段内的ip可以访问。 IP地址和掩码均知道时才能确定主机所在的网段,也就是用这个原理来限制可访问的IP网段了。 ip后面加上“/N”就代表掩码的二进制”1“有N位。 例如: ①0.0.0.0/0 主机ip地…...
PMP项目管理主要学习内容是什么?
PMP项目管理是指根据美国项目管理学会(Project Management Institute,简称PMI)制定的项目管理知识体系和方法论进行项目管理的一种认证。PMP主要关注项目的规划、执行和控制等方面的知识和技能。 下面是PMP项目管理《PMBOK指南》第六版的主要学习内容: …...
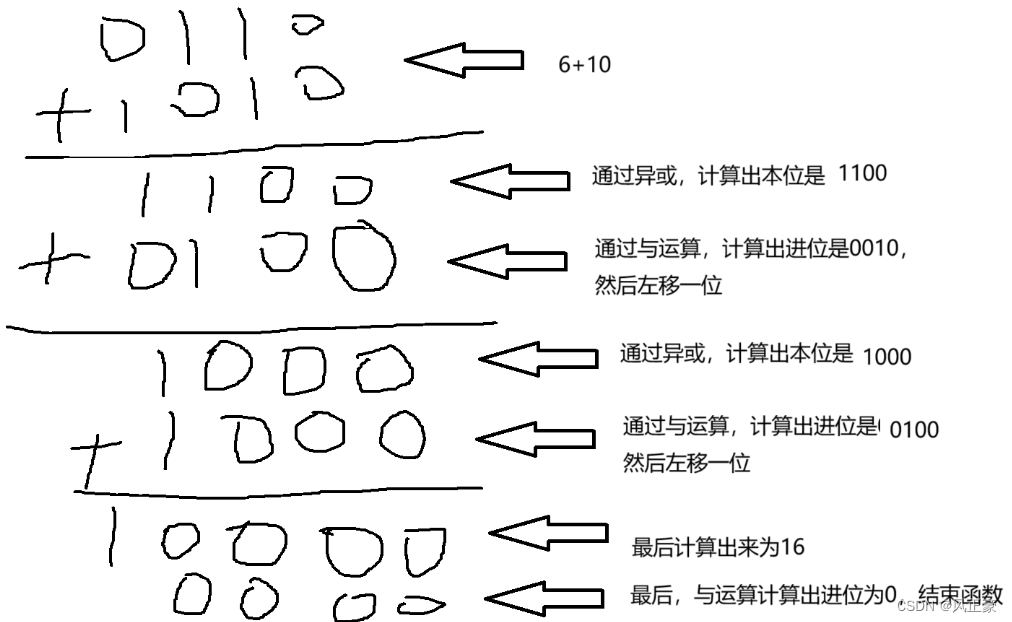
小米面试题——不用加减乘除计算两数之和
前言 (1)刷B站看到一个面试题,不用加减乘除计算两数之和。 (2)当时我看到这个题目,第一反应就是感觉这是一个数电题目。不过需要采用C语言的方式编写出来。 (3)不过看到大佬的代码之…...

Mysql 日志管理 数据备份
MySQL日志管理 MySQL的默认日志保存位置为/usr/local/mysql/data 日志开启方式有两种:通过配置文件或者是通过命令 通过命令修改开启的日志是临时的,关闭或重启服务后就会关闭 日志的分类 1.错误日志 用来记录当MySQL启动、停止或运行时发生的错误信…...

Java小记-腾讯2020校招-后台-逛街
题目描述: 小Q在周末的时候和他的小伙伴来到大城市逛街,一条步行街上有很多高楼,共有n座高楼排成一行。 小Q从第一栋一直走到了最后一栋,小Q从来都没有见到这么多的楼,所以他想知道他在每栋楼的位置处能看到多少栋楼呢…...
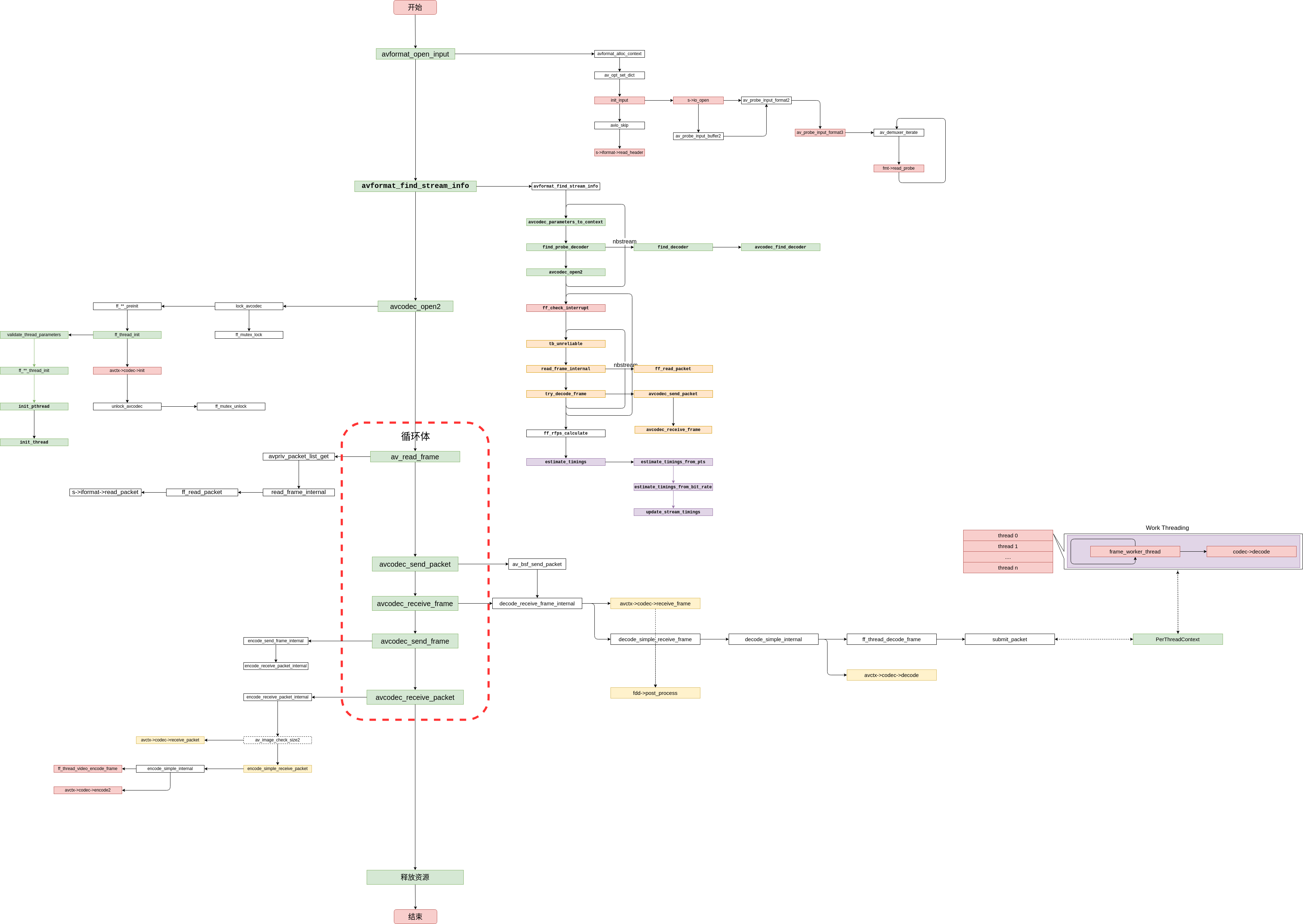
FFmpeg5.0源码阅读——FFmpeg大体框架
摘要:前一段时间熟悉了下FFmpeg主流程源码实现,对FFmpeg的整体框架有了个大概的认识,因此在此做一个笔记,希望以比较容易理解的文字描述FFmpeg本身的结构,加深对FFmpeg的框架进行梳理加深理解,如果文章中有…...

【算法刷题之字符串篇】
目录 1.leetcode-344. 反转字符串(1)方法:双指针 2.leetcode-541. 反转字符串 II(1)方法一:模拟(2)方法二:双指针 3.leetcode-剑指 Offer 05. 替换空格(1&…...

js中forEach和map的区别:forEach不会改变原数组,而map会改变数组?错了错了
1.提出思考?forEach不会改变原数组,而map会改变数组? 看到掘金上一篇文章觉得很有意思:大致是描述一般面试官问js中forEach和map的区别?都会回答forEach不会改变原数组,而map会改变,我也一直对…...

深度对话:从底层看Sui设计理念及网络规模扩展
近日,我们采访了George Danezis以了解Sui的交易处理系统如何促成高性能网络。他是Mysten Labs的联合创始人和首席科学家(Sui的最初贡献者),也是伦敦大学学院(University College London,UCL)安全…...

2.单链表练习
1. 链表的基本概念 链表(Linked List)是一种常见的数据结构,用于存储一系列元素,这些元素可以是任意类型的数据。链表中的每个元素被称为节点(Node),每个节点包含两部分:一个存储数…...

Wordpress 安装插件和主题报错
安装主题和插件的时候,就是这个恶心的报错, Wordpress plugin install: Could not create directory 这是权限惹的祸,如下一顿操作猛如虎,就解决了。 sudo chown -R www:www wp-content/themes sudo chown -R www:www wp-conte…...
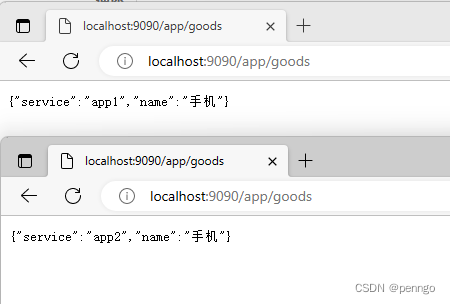
Spring Cloud 2022.x版本使用gateway和nacos实现动态路由和负载均衡
文章目录 1、nacos下载安装1.1、启动服务器1.2、关闭服务器1.3、服务注册&发现和配置管理接口 2、代码示例2.1、app1工程代码2.2、app2工程代码2.3、gateway网关工程代码 3、动态配置网关路由3.1、配置动态路由3.2、配置为负载模式 4、gateway配置规则4.1、请求转发&#x…...

CSS中如何隐藏元素但保留其占位空间(display:none vs visibility:hidden)?
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ display: none;⭐ visibility: hidden;⭐ 如何选择⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本专栏哦 几何带你启航前端之旅 欢迎来到前端入门之旅!这个专栏是为…...

无涯教程-机器学习 - 数据可视化
在上一章中,无涯教程讨论了数据对于机器学习算法的重要性,以了解具有统计信息的数据,还有另一种称为可视化的方式来理解数据。 借助数据可视化,可以看到数据的属性保持什么样的关联,这是查看要素是否与输出相对应的最…...

JavaSec-RCE
简介 RCE(Remote Code Execution),可以分为:命令注入(Command Injection)、代码注入(Code Injection) 代码注入 1.漏洞场景:Groovy代码注入 Groovy是一种基于JVM的动态语言,语法简洁,支持闭包、动态类型和Java互操作性,…...

OpenLayers 可视化之热力图
注:当前使用的是 ol 5.3.0 版本,天地图使用的key请到天地图官网申请,并替换为自己的key 热力图(Heatmap)又叫热点图,是一种通过特殊高亮显示事物密度分布、变化趋势的数据可视化技术。采用颜色的深浅来显示…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

【Web 进阶篇】优雅的接口设计:统一响应、全局异常处理与参数校验
系列回顾: 在上一篇中,我们成功地为应用集成了数据库,并使用 Spring Data JPA 实现了基本的 CRUD API。我们的应用现在能“记忆”数据了!但是,如果你仔细审视那些 API,会发现它们还很“粗糙”:有…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

免费PDF转图片工具
免费PDF转图片工具 一款简单易用的PDF转图片工具,可以将PDF文件快速转换为高质量PNG图片。无需安装复杂的软件,也不需要在线上传文件,保护您的隐私。 工具截图 主要特点 🚀 快速转换:本地转换,无需等待上…...

如何更改默认 Crontab 编辑器 ?
在 Linux 领域中,crontab 是您可能经常遇到的一个术语。这个实用程序在类 unix 操作系统上可用,用于调度在预定义时间和间隔自动执行的任务。这对管理员和高级用户非常有益,允许他们自动执行各种系统任务。 编辑 Crontab 文件通常使用文本编…...

Axure 下拉框联动
实现选省、选完省之后选对应省份下的市区...
0609)
书籍“之“字形打印矩阵(8)0609
题目 给定一个矩阵matrix,按照"之"字形的方式打印这个矩阵,例如: 1 2 3 4 5 6 7 8 9 10 11 12 ”之“字形打印的结果为:1,…...
