【数据结构】复杂度讲解
目录
时间复杂度与空间复杂度::
1.算法效率
2.时间复杂度
3.空间复杂度
4.常见时间复杂度以及复杂度OJ练习
时间复杂度与空间复杂度::
什么是数据结构?
数据结构中是计算机存储,组织数据的方式,指相互之间存在一种或多种特定关系的数据元素的集合.
什么是算法?
算法是定义良好的计算过程,它取一个或一组的值为输入,并产生一个或一组值作为输出.简单来说
算法就是一系列的计算步骤,用来将输入数据转化成输出结果.
例如:数据结构是在内存中管理数据——增删查改
数据库是在磁盘中管理数据——增删查改
B树用到二分查找算法 去重要用到搜索树
1.算法效率
算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源,因此衡量一个算法的好坏
一般是从时间和空间两个维度来衡量的,即时间复杂度和空间复杂度.
时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间
在计算机发展的早期,计算机的存储容量很小,所以对空间复杂度很是在乎,但是经过计算机行业的
迅速发展,计算机的存储容量已经达到了很高的程度,所以我们如今已经不需要再特别关注一个算法的空间复杂度.
摩尔定律:集成电路上可以容纳的晶体管数目在大约每经过18个月便会增加一倍.
2.时间复杂度
时间复杂度的概念:
时间复杂度的定义:在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间.
一个算法执行所耗费的时间,从理论上来说是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道.
但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方式.
一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作执行次数,为算法的时间复杂度.
即:找到某条语句与问题规模N之间的数学表达式,就是算出了该算法的时间复杂度.
void Func1(int N)
{int count = 0;for (int i = 0; i < N; ++i){for (int j = 0; j < N; ++i){++count;}}for (int k = 0; k < 2 * N; ++k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}
时间复杂度为:O(N^2)
void Func2(int N)
{int count = 0;for (int k = 0; k < 2 * N; ++k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}
时间复杂度为:O(N)
void Func3(int N, int M)
{int count = 0;for (int k = 0; k < M; ++k){++count;}for (int k = 0; k < N; ++k){++count;}printf("%d\n", count);
}
时间复杂度为:O(M+N)
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange = 0)break;}
}
时间复杂度为:O(N^2)
void Fun4(int N)
{int count = 0;for (int k = 0; k < 100; ++k){++count;}printf("%d\n", count);
}
时间复杂度为:O(1)大O的渐进表示法:
大O符号是用于描述函数渐进行为的数学符号.
推导大O渐进表示法:
1.用常数1取代运行时间中的所有加法常数.
2.在修改后的运行次数函数中,只保留最高阶项.
3.如果最高阶系数存在且不是1,则去掉与这个项目相乘的常数,得到的结果就是大O阶.
算法的时间复杂度存在最好,最坏和平均情况:
最坏情况:任意输入规模的最大运行次数(上界)
平均情况:任意输入规模的期望运行次数
最好情况:任意输入规模的最小运行次数(下界)
例如:在一个长度为N的数组中搜索一个数据x
最好情况:1次找到
最坏情况:N次找到
平均情况:N/2次找到
在实际情况中关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n - 1;//[begin,end] begin和end是左闭右闭区间,因此有=号while (begin <= end){int mid = begin + ((end - begin) >> 1);if (a[mid] < x)begin = mid + 1;else if (a[mid] > x)end = mid - 1;elsereturn mid;}return -1;
}
二分查找的最好情况是O(1)
二分查找的最坏情况是找不到 时间复杂度为O(logN)
每查找一次 查找区间个数减少一半(除2)
N/2/2/2.../2 = 1
longlong Fac(size_t N)
{if (1 == N)return 1;return Fac(N - 1) * N;
}
时间复杂度为O(N)
longlong Fib(size_t N)
{if (N < 3)return 1;return Fib(N - 1) + Fib(N - 2);
}
时间复杂度为O(2^N)
longlong Fib(size_t N)
{if (N < 3)return 1;longlong f1 = 1, f2 = 1, f3;for (size_t i = 3; i <= N; ++i){f3 = f2 + f1;f1 = f2;f2 = f3;}return f3;
}
时间复杂度为O(N)3.空间复杂度
空间复杂度也是一个数学表达式,是对一个算法在运行过程中额外占用存储空间大小的量度.
空间复杂度不是程序占用了多少字节的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数.
空间复杂度计算规则基本跟时间复杂度类似,也使用大O的渐进表示法.
注意:函数运行时所需要的栈空间(存储参数,局部变量,一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时侯显示申请的额外空间来确定.
1G大约10亿字节 1G = 1024*1024*1024
1M大约100万字节 1M = 1024*1024
计算BubbleSort的空间复杂度
void BubbleSort(int* a, int n)
{assert(a);for (size_t end = n; end > 0; --end){int exchange = 0;for (size_t i = 1; i < end; ++i){if (a[i - 1] > a[i]){Swap(&a[i - 1], &a[i]);exchange = 1;}}if (exchange == 0)break;}
}
空间复杂度为O(1)
计算Fac的空间复杂度
longlong Fac(size_t N)
{if (N == 0)return 1;return Fac(N - 1) * N;
}
空间复杂度为O(N)
每个函数栈帧是常数个 有N+1个Fac栈帧
计算Fib的空间复杂度
longlong Fib(size_t N)
{if (N < 3)return 1;return Fib(N - 1) + Fib(N - 2);
}
空间复杂度为O(N)4.常见时间复杂度以及复杂度OJ练习
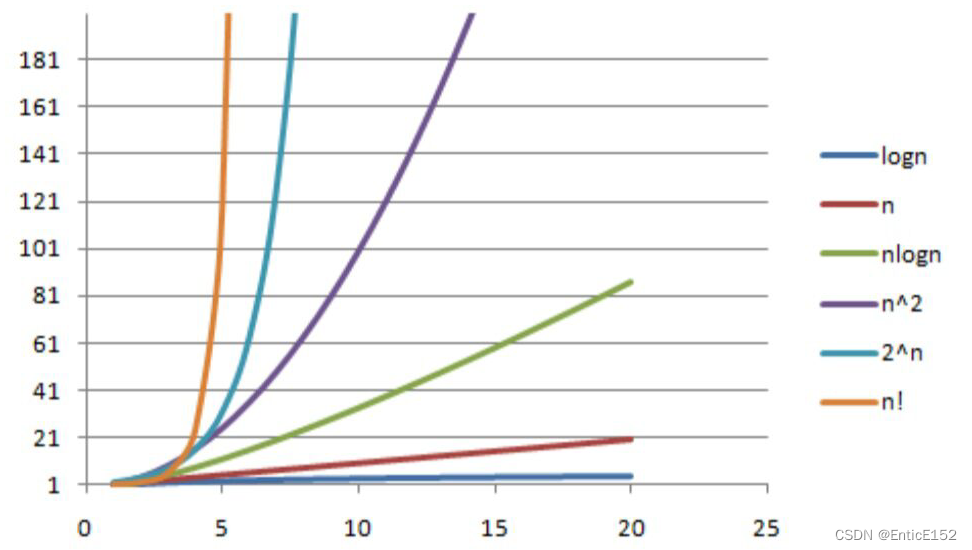
一般算法常见的复杂度如下:
| 5201314 | O(1) | 常数阶 |
| 3n+4 | O(n) | 线性阶 |
| 3n^2+4n+5 | O(n^2) | 平方阶 |
| 3log(2)n+4 | O(logn) | 对数阶 |
| 2n+3nlog(2)n+14 | O(n*logn) | nlogn阶 |
| n^3+2n^2+4n+6 | O(n^3) | 立方阶 |
| 2^n | O(2^n) | 指数阶 |
复杂度的OJ练习:
消失的数字OJ链接:https://leetcode-cn.com/problems/missing-number-lcci/
int missingNumber(int* nums, int numSize)
{int x = 0;for (int i = 0; i < numSize; ++i){x ^= nums[i];}for (int j = 0; i < numSize + 1; ++j){x ^= j;}return x;
}void reverse(int* a, int begin, int end)
{while (begin < end){int tmp = a[begin];a[begin] = a[end];a[end] = tmp;++begin;--end;}
}
void rotate(int* num, int numSize, int k)
{if (k > numSize)k %= numSize;reverse(nums, 0, numsSize - k - 1);reverse(nums, numSize - k, numsSize - 1);reverse(nums, 0, numsSize - 1);
}相关文章:

【数据结构】复杂度讲解
目录 时间复杂度与空间复杂度:: 1.算法效率 2.时间复杂度 3.空间复杂度 4.常见时间复杂度以及复杂度OJ练习 时间复杂度与空间复杂度:: 什么是数据结构? 数据结构中是计算机存储,组织数据的方式,指相互之间存在一种或多种特定关…...

JAVA-线程池技术
目录 概念 什么是线程? 什么是线程池? 线程池出现背景 线程池原理图 JAVA提供线程池 线程池参数 如果本篇博客对您有一定的帮助,大家记得留言点赞收藏哦。 概念 什么是线程? 是操作系统能够进行运算调度的最小单位。&am…...
)
【C++】从0到1入门C++编程学习笔记 - 提高编程篇:STL常用算法(算术生成算法)
文章目录一、accumulate二、fill学习目标: 掌握常用的算术生成算法 注意: 算术生成算法属于小型算法,使用时包含的头文件为 #include <numeric> 算法简介: accumulate // 计算容器元素累计总和 fill // 向容器中添加元…...

【C++】static成员
💙作者:阿润菜菜 📖专栏:C 目录 概念 特性 出个题 概念 声明为static的类成员称为类的静态成员,用static修饰的成员变量,称之为静态成员变量; 用static修饰的成员函数,称之为静态…...
Python Scrapy 爬虫简单教程
1. Scrapy install 准备知识 pip 包管理Python 安装XpathCssWindows安装 Scrapy $>- pip install scrapy Linux安装 Scrapy $>- apt-get install python-scrapy 2. Scrapy 项目创建 在开始爬取之前,必须创建一个新的Scrapy项目。进入自定义的项目目录中&am…...
【DOCKER】容器概念基础
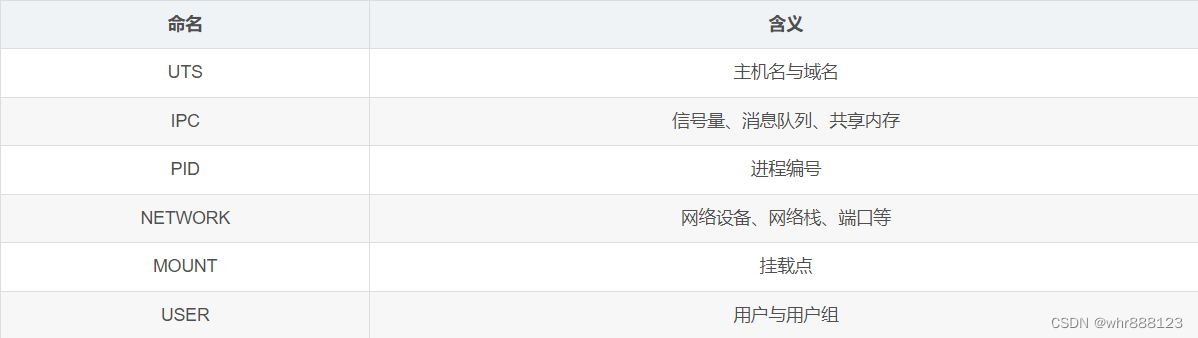
文章目录1.容器1.概念2.特点3.与虚拟机的对比2.docker1.概念2.命名空间3.核心概念3.命令1.镜像命令2.仓库命令1.容器 1.概念 1.不同的运行环境,底层架构是不同的,这就会导致测试环境运行好好的应用,到了生产环境就会出现bug(就像…...
第九层(16):STL终章——常用集合算法
文章目录前情回顾常用集合算法set_intersectionset_unionset_difference最后一座石碑倒下,爬塔结束一点废话🎉welcome🎉 ✒️博主介绍:一名大一的智能制造专业学生,在学习C/C的路上会越走越远,后面不定期更…...

一起学习用Verilog在FPGA上实现CNN----(六)SoftMax层设计
1 SoftMax层设计 1.1 softmax SoftMax函数的作用是输入归一化,计算各种类的概率,即计算0-9数字的概率,SoftMax层的原理图如图所示,输入和输出均为32位宽的10个分类,即32x10320 本项目softmax实现逻辑为: …...

pixhawk2.4.8-APM固件-MP地面站配置过程记录
目录一、硬件准备二、APM固件、MP地面站下载三、地面站配置1 刷固件2 机架选择3 加速度计校准4 指南针校准5 遥控器校准6 飞行模式7 紧急断电&无头模式8 基础参数设置9 电流计校准10 电调校准11 起飞前检查(每一项都非常重要)12 飞行经验四、遇到的问…...
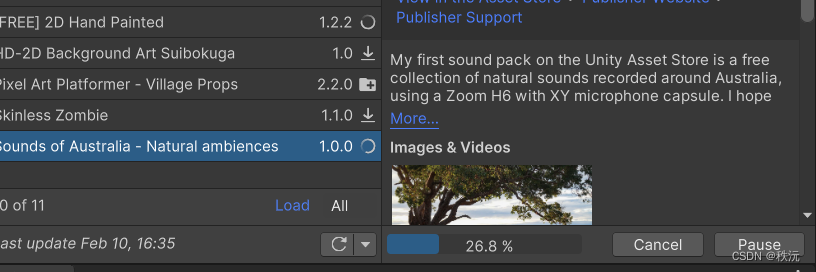
【unity细节】关于资源商店(Package Maneger)无法下载资源问题的解决
👨💻个人主页:元宇宙-秩沅 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 本文由 秩沅 原创 收录于专栏:unity细节和bug ⭐关于资源商店为何下载不了的问题⭐ 文章目录⭐关于资源商店为何下载不了的问题…...

[Arxiv 2022] A Novel Plug-in Module for Fine-Grained Visual Classification
Contents MethodPlug-in ModuleLoss functionExperimentsReferencesMethod Plug-in Module Backbone:为了帮助模型抽取出不同尺度的特征,作者在 backbone 里加入了 FPNWeakly Supervised Selector:假设 backbone 的 i i...
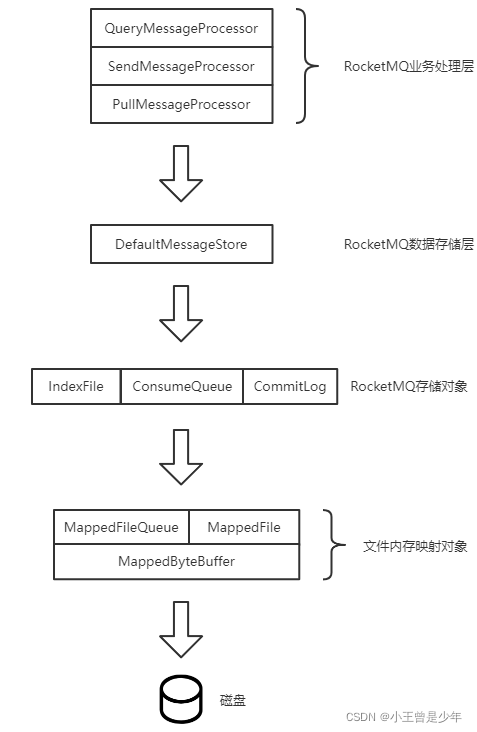
RocketMQ Broker消息处理流程及部分源码解析
🍊 Java学习:Java从入门到精通总结 🍊 深入浅出RocketMQ设计思想:深入浅出RocketMQ设计思想 🍊 绝对不一样的职场干货:大厂最佳实践经验指南 📆 最近更新:2023年2月10日 &#x…...
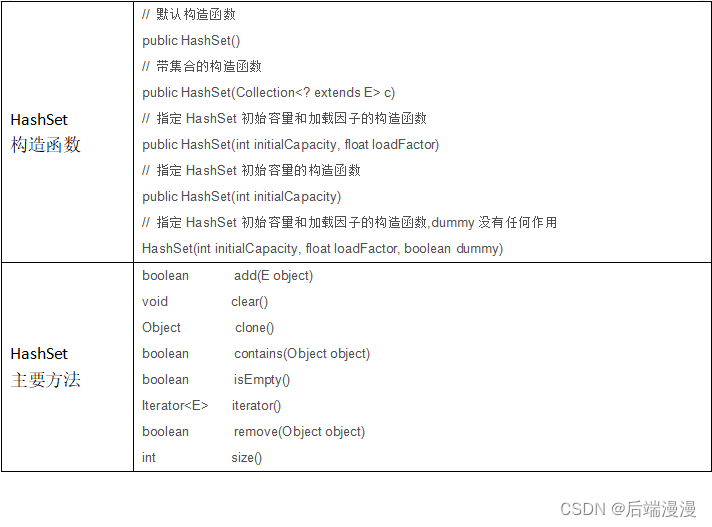
Java面试题:Java集合框架
文章目录一、Java集合框架二、Java集合特性三、各集合类的使用ArrayListLinkedListHashSetHashSet源码解析对源码进行总结HashSet可同步HashSet的使用HashMap四、Iterator迭代器五、遍历集合元素的若干方式参考文章:Hash详解参考文章:深入浅出学Java——…...

时间之间的比较与计算相差年、月、日、小时、分钟、毫秒、纳秒以及判断闰年--LocalDateTime
如何把String/Date转成LocalDateTime参考String、Date与LocalDate、LocalTime、LocalDateTime之间互转 String、Date、LocalDateTime、Calendar与时间戳之间互相转化参考String、Date、LocalDateTime、Calendar与时间戳之间互相转化 比较方法介绍 isBefore(ChronoLocalDateT…...

PyTorch学习笔记:nn.L1Loss——L1损失
PyTorch学习笔记:nn.L1Loss——L1损失 torch.nn.L1Loss(size_averageNone, reduceNone, reductionmean)功能:创建一个绝对值误差损失函数,即L1损失: l(x,y)L{l1,…,lN}T,ln∣xn−yn∣l(x,y)L\{l_1,\dots,l_N\}^T,l_n|x_n-y_n| l(…...
Java程序设计-ssm企业财务管理系统设计与实现
摘要系统设计系统实现开发环境:摘要 对于企业集来说,财务管理的地位很重要。随着计算机和网络在企业中的广泛应用,企业发展速度在不断加快,在这种市场竞争冲击下企业财务管理系统必须优先发展,这样才能保证在竞争中处于优势地位。…...

疑难杂症篇(二十一)--Ubuntu18.04安装usb-cam过程出现的问题
对Ubuntu18.04{\rm Ubuntu 18.04}Ubuntu18.04环境下的ROS{\rm ROS}ROS的melodic{\rm melodic}melodic版本安装usb−cam{\rm usb-cam}usb−cam过程出现的两个常见问题提出解决方案。 1.问题1:usb-cam功能包编译时出现"未定义的引用"的问题 问题描述&#…...

npm-npm i XX --save 和--save-dev
之前使用npm i XX --save 和--save-dev 没太在意,就想记录一下,查到一篇比较全的(链接:NPM install -save 和 -save-dev 傻傻分不清),直接看好了,哈哈~ # 安装模块到项目目录下 npm install moduleName # -g 的意思是…...
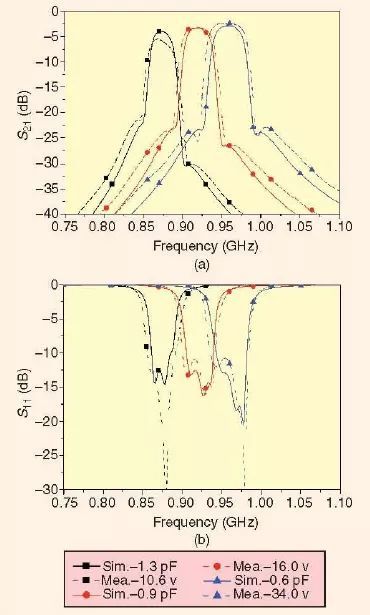
可重构或可调谐微波滤波器技术
电子可重构,或者说电调微波滤波器由于其在改善现在及未来微波系统容量中不断提高的重要性而正吸引着人们越来越多的关注来对其进行研究和开发。例如,崭露头脚的超宽带(UWB)技术要求使用很宽的无线电频谱。然而,作为资源…...
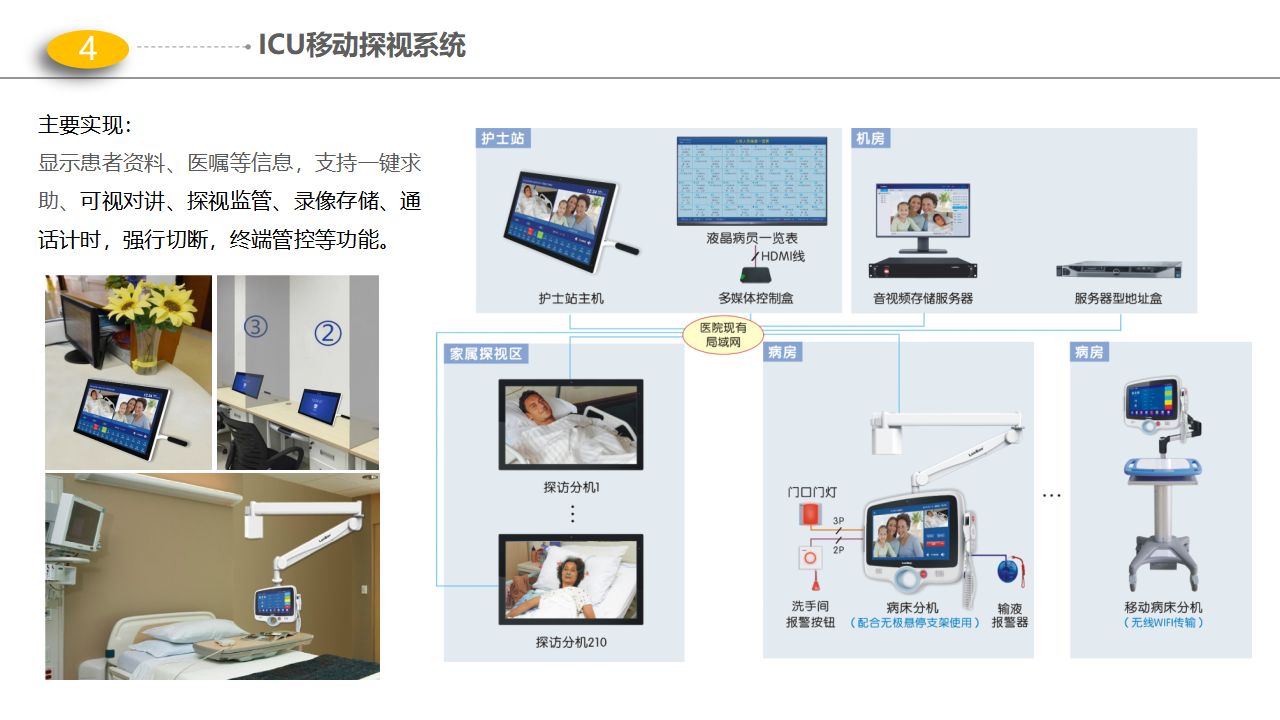
医院智能化解决方案-门(急)诊、医技、智能化项目解决方案
【版权声明】本资料来源网络,知识分享,仅供个人学习,请勿商用。【侵删致歉】如有侵权请联系小编,将在收到信息后第一时间删除!完整资料领取见文末,部分资料内容:篇幅有限,无法完全展…...

Python爬虫实战:研究MechanicalSoup库相关技术
一、MechanicalSoup 库概述 1.1 库简介 MechanicalSoup 是一个 Python 库,专为自动化交互网站而设计。它结合了 requests 的 HTTP 请求能力和 BeautifulSoup 的 HTML 解析能力,提供了直观的 API,让我们可以像人类用户一样浏览网页、填写表单和提交请求。 1.2 主要功能特点…...

未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?
编辑:陈萍萍的公主一点人工一点智能 未来机器人的大脑:如何用神经网络模拟器实现更智能的决策?RWM通过双自回归机制有效解决了复合误差、部分可观测性和随机动力学等关键挑战,在不依赖领域特定归纳偏见的条件下实现了卓越的预测准…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

微服务商城-商品微服务
数据表 CREATE TABLE product (id bigint(20) UNSIGNED NOT NULL AUTO_INCREMENT COMMENT 商品id,cateid smallint(6) UNSIGNED NOT NULL DEFAULT 0 COMMENT 类别Id,name varchar(100) NOT NULL DEFAULT COMMENT 商品名称,subtitle varchar(200) NOT NULL DEFAULT COMMENT 商…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

Go 语言并发编程基础:无缓冲与有缓冲通道
在上一章节中,我们了解了 Channel 的基本用法。本章将重点分析 Go 中通道的两种类型 —— 无缓冲通道与有缓冲通道,它们在并发编程中各具特点和应用场景。 一、通道的基本分类 类型定义形式特点无缓冲通道make(chan T)发送和接收都必须准备好࿰…...

LangChain知识库管理后端接口:数据库操作详解—— 构建本地知识库系统的基础《二》
这段 Python 代码是一个完整的 知识库数据库操作模块,用于对本地知识库系统中的知识库进行增删改查(CRUD)操作。它基于 SQLAlchemy ORM 框架 和一个自定义的装饰器 with_session 实现数据库会话管理。 📘 一、整体功能概述 该模块…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...
