算法训练day34|贪心算法 part03(LeetCode 1005.K次取反后最大化的数组和、134. 加油站、135. 分发糖果(处理一边再处理一边))
文章目录
- 1005.K次取反后最大化的数组和
- 思路分析
- 代码实现
- 134. 加油站
- 暴力方法
- 贪心方法
- 135. 分发糖果(处理一边再处理一边)
- 思路分析
- 代码实现
- 思考总结
1005.K次取反后最大化的数组和
题目链接🔥
给定一个整数数组 A,我们只能用以下方法修改该数组:我们选择某个索引 i 并将 A[i] 替换为 -A[i],然后总共重复这个过程 K 次。(我们可以多次选择同一个索引 i。)
以这种方式修改数组后,返回数组可能的最大和。
示例 1:
输入:A = [4,2,3], K = 1
输出:5
解释:选择索引 (1,) ,然后 A 变为 [4,-2,3]。
示例 2:
输入:A = [3,-1,0,2], K = 3
输出:6
解释:选择索引 (1, 2, 2) ,然后 A 变为 [3,1,0,2]。
示例 3:
输入:A = [2,-3,-1,5,-4], K = 2
输出:13
解释:选择索引 (1, 4) ,然后 A 变为 [2,3,-1,5,4]。
提示:
1 <= A.length <= 10000
1 <= K <= 10000
-100 <= A[i] <= 100
思路分析
局部最优:让绝对值大的负数变为正数,当前数值达到最大,整体最优:整个数组和达到最大。
局部最优可以推出全局最优。
那么如果将负数都转变为正数了,K依然大于0,此时的问题是一个有序正整数序列,如何转变K次正负,让 数组和 达到最大。
那么又是一个贪心:
局部最优:只找数值最小的正整数进行反转,当前数值和可以达到最大(例如正整数数组{5, 3, 1},反转1 得到-1 比 反转5得到的-5 大多了),
全局最优:整个 数组和 达到最大。
那么本题的解题步骤为:
- 第一步:将数组按照绝对值大小从大到小排序,注意要按照绝对值的大小
- 第二步:从前向后遍历,遇到负数将其变为正数,同时K–
- 第三步:如果K还大于0,那么反复转变数值最小的元素,将K用完
- 第四步:求和
代码实现
class Solution {
public:static bool compare(int a,int b){return(abs(a)>abs(b));}int largestSumAfterKNegations(vector<int>& nums, int k) {sort(nums.begin(),nums.end(),compare);for(int i=0;i<nums.size()&&k>0;i++){if(nums[i]<0){nums[i]*=-1;k--;}}if(k%2==1) nums[nums.size()-1]*=-1;int result=0;for(int i=0;i<nums.size();i++) {cout<<nums[i];result+=nums[i];}return result;}
};
记录一个错误
第一次写成这样了
class Solution {
public:bool compare(int a,int b){//注意这里return(abs(a)>abs(b));}int largestSumAfterKNegations(vector<int>& nums, int k) {sort(nums.begin(),nums.end(),compare);...}
};
就报错了,这是因为compare 函数是一个非静态成员函数,这意味着它与类的实例相关联。然而,在调用 sort 函数时,它期望一个普通的(非成员函数)比较器。
两种可能的方法
方法 1:将 compare 定义为静态成员函数
class Solution {
public:static bool compare(int a, int b) {return (abs(a) > abs(b));}int largestSumAfterKNegations(vector<int>& nums, int k) {sort(nums.begin(), nums.end(), compare);// 其他部分保持不变}
};
方法 2:将 compare 定义在类的外部
bool compare(int a, int b) {return (abs(a) > abs(b));
}class Solution {
public:int largestSumAfterKNegations(vector<int>& nums, int k) {sort(nums.begin(), nums.end(), compare);// 其他部分保持不变}
};
这两种方法都将 compare 函数与类的实例无关,从而可以在 sort 函数中正常使用。
134. 加油站
题目链接🔥🔥
在一条环路上有 N 个加油站,其中第 i 个加油站有汽油 gas[i] 升。
你有一辆油箱容量无限的的汽车,从第 i 个加油站开往第 i+1 个加油站需要消耗汽油 cost[i] 升。你从其中的一个加油站出发,开始时油箱为空。
如果你可以绕环路行驶一周,则返回出发时加油站的编号,否则返回 -1。
说明:
如果题目有解,该答案即为唯一答案。
输入数组均为非空数组,且长度相同。
输入数组中的元素均为非负数。
示例 1: 输入:
gas = [1,2,3,4,5]
cost = [3,4,5,1,2]
输出: 3 解释:
- 从 3 号加油站(索引为 3 处)出发,可获得 4 升汽油。此时油箱有 = 0 + 4 = 4 升汽油
- 开往 4 号加油站,此时油箱有 4 - 1 + 5 = 8 升汽油
- 开往 0 号加油站,此时油箱有 8 - 2 + 1 = 7 升汽油
- 开往 1 号加油站,此时油箱有 7 - 3 + 2 = 6 升汽油
- 开往 2 号加油站,此时油箱有 6 - 4 + 3 = 5 升汽油
- 开往 3 号加油站,你需要消耗 5 升汽油,正好足够你返回到 3 号加油站。
- 因此,3 可为起始索引。
示例 2: 输入:
gas = [2,3,4]
cost = [3,4,3]
输出: -1
解释: 你不能从 0 号或 1 号加油站出发,因为没有足够的汽油可以让你行驶到下一个加油站。我们从 2 号加油站出发,可以获得 4 升汽油。 此时油箱有 = 0 + 4 = 4 升汽油。开往 0 号加油站,此时油箱有 4 - 3 + 2 = 3 升汽油。开往 1 号加油站,此时油箱有 3 - 3 + 3 = 3 升汽油。你无法返回 2 号加油站,因为返程需要消耗 4 升汽油,但是你的油箱只有 3 升汽油。因此,无论怎样,你都不可能绕环路行驶一周。
暴力方法
暴力的方法很明显就是O(n^2)的,遍历每一个加油站为起点的情况,模拟一圈。
如果跑了一圈,中途没有断油,而且最后油量大于等于0,说明这个起点是ok的。
暴力的方法思路比较简单,但代码写起来也不是很容易,关键是要模拟跑一圈的过程。
for循环适合模拟从头到尾的遍历,而while循环适合模拟环形遍历,要善于使用while!
C++代码如下:
class Solution {
public:int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {for (int i = 0; i < cost.size(); i++) {int rest = gas[i] - cost[i]; // 记录剩余油量int index = (i + 1) % cost.size();while (rest > 0 && index != i) { // 模拟以i为起点行驶一圈(如果有rest==0,那么答案就不唯一了)rest += gas[index] - cost[index];index = (index + 1) % cost.size();}// 如果以i为起点跑一圈,剩余油量>=0,返回该起始位置if (rest >= 0 && index == i) return i;}return -1;}
};
贪心方法
如果总油量减去总消耗大于等于零那么一定可以跑完一圈,说明 各个站点的加油站 剩油量rest[i]相加一定是大于等于零的。
每个加油站的剩余量rest[i]为gas[i] - cost[i]。
i从0开始累加rest[i],和记为curSum,一旦curSum小于零,说明[0, i]区间都不能作为起始位置,因为这个区间选择任何一个位置作为起点,到i这里都会断油,那么起始位置从i+1算起,再从0计算curSum。
如图:

那么为什么一旦[0,i] 区间和为负数,起始位置就可以是i+1呢,i+1后面就不会出现更大的负数?
如果出现更大的负数,就是更新i,那么起始位置又变成新的i+1了。
那有没有可能 [0,i] 区间 选某一个作为起点,累加到 i这里 curSum是不会小于零呢? 如图:

如果 curSum<0 说明 区间和1 + 区间和2 < 0, 那么 假设从上图中的位置开始计数curSum不会小于0的话,就是 区间和2>0。
区间和1 + 区间和2 < 0 同时 区间和2>0,只能说明区间和1 < 0, 那么就会从假设的箭头初就开始从新选择其实位置了。
那么局部最优:当前累加rest[i]的和curSum一旦小于0,起始位置至少要是i+1,因为从i之前开始一定不行。全局最优:找到可以跑一圈的起始位置。
局部最优可以推出全局最优,找不出反例,试试贪心!
整体代码:
class Solution {
public:int canCompleteCircuit(vector<int>& gas, vector<int>& cost) {int curSum=0;int totalSum=0;int startIndex=0;for(int i=0;i<gas.size();i++){curSum+=gas[i]-cost[i];totalSum+=gas[i]-cost[i];if(curSum<0) { // 当前累加rest[i]和 curSum一旦小于0curSum=0; // 起始位置更新为i+1startIndex=i+1; // curSum从0开始 }}if(totalSum<0) return -1; // 说明怎么走都不可能跑一圈了return startIndex;}
};
135. 分发糖果(处理一边再处理一边)
题目链接🔥🔥🔥
老师想给孩子们分发糖果,有 N 个孩子站成了一条直线,老师会根据每个孩子的表现,预先给他们评分。
你需要按照以下要求,帮助老师给这些孩子分发糖果:
- 每个孩子至少分配到 1 个糖果。
- 相邻的孩子中,评分高的孩子必须获得更多的糖果。
那么这样下来,老师至少需要准备多少颗糖果呢?
示例 1:
输入: [1,0,2]
输出: 5
解释: 你可以分别给这三个孩子分发 2、1、2 颗糖果。
示例 2:
输入: [1,2,2]
输出: 4
解释: 你可以分别给这三个孩子分发 1、2、1 颗糖果。第三个孩子只得到 1 颗糖果,这已满足上述两个条件。
思路分析
这道题目一定是要确定一边之后,再确定另一边,例如比较每一个孩子的左边,然后再比较右边,如果两边一起考虑一定会顾此失彼。
先确定右边评分大于左边的情况(也就是从前向后遍历)
此时局部最优:只要右边评分比左边大,右边的孩子就多一个糖果,全局最优:相邻的孩子中,评分高的右孩子获得比左边孩子更多的糖果
局部最优可以推出全局最优。
如果ratings[i] > ratings[i - 1] 那么[i]的糖 一定要比[i - 1]的糖多一个,所以贪心:candyVec[i] = candyVec[i - 1] + 1
// 从前向后
for (int i = 1; i < ratings.size(); i++) {if (ratings[i] > ratings[i - 1]) candyVec[i] = candyVec[i - 1] + 1;
}

再确定左孩子大于右孩子的情况(从后向前遍历)
遍历顺序这里有同学可能会有疑问,为什么不能从前向后遍历呢?
因为 rating[5]与rating[4]的比较 要利用上 rating[5]与rating[6]的比较结果,所以 要从后向前遍历。
如果从前向后遍历,rating[5]与rating[4]的比较 就不能用上 rating[5]与rating[6]的比较结果了 。如图:

所以确定左孩子大于右孩子的情况一定要从后向前遍历!
如果 ratings[i] > ratings[i + 1],此时candyVec[i](第i个小孩的糖果数量)就有两个选择了,一个是candyVec[i + 1] + 1(从右边这个加1得到的糖果数量),一个是candyVec[i](之前比较右孩子大于左孩子得到的糖果数量)。
那么又要贪心了,局部最优:取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量,保证第i个小孩的糖果数量既大于左边的也大于右边的。全局最优:相邻的孩子中,评分高的孩子获得更多的糖果。
局部最优可以推出全局最优。
所以就取candyVec[i + 1] + 1 和 candyVec[i] 最大的糖果数量,candyVec[i]只有取最大的才能既保持对左边candyVec[i - 1]的糖果多,也比右边candyVec[i + 1]的糖果多。

// 从后向前
for (int i = ratings.size() - 2; i >= 0; i--) {if (ratings[i] > ratings[i + 1] ) {candyVec[i] = max(candyVec[i], candyVec[i + 1] + 1);}
}
代码实现
class Solution {
public:int candy(vector<int>& ratings) {int result=0;vector<int> candy(ratings.size(),1);for(int i=1;i<ratings.size();i++){if(ratings[i]>ratings[i-1]) candy[i]=candy[i-1]+1;}for(int i=ratings.size()-1;i>0;i--){if(ratings[i]<ratings[i-1]) candy[i-1]=max(candy[i]+1,candy[i-1]);}for(int candy:candy){result+=candy;}return result;}
};
思考总结
本题涉及到一个思想,就是想处理好一边再处理另一边,不要两边想着一起兼顾
采用了两次贪心的策略:
- 一次是从左到右遍历,只比较右边孩子评分比左边大的情况。
- 一次是从右到左遍历,只比较左边孩子评分比右边大的情况。
相关文章:

算法训练day34|贪心算法 part03(LeetCode 1005.K次取反后最大化的数组和、134. 加油站、135. 分发糖果(处理一边再处理一边))
文章目录 1005.K次取反后最大化的数组和思路分析代码实现 134. 加油站暴力方法贪心方法 135. 分发糖果(处理一边再处理一边)思路分析代码实现思考总结 1005.K次取反后最大化的数组和 题目链接🔥 给定一个整数数组 A,我们只能用以下方法修改该数组&#…...

插入排序和冒泡排序
文章目录 1、插入排序2、冒泡排序 1、插入排序 流程如下: 1)从第一个元素开始遍历,该元素可以认为已经被排序,记录已排序序列的结尾元素为end i 2)取下一个元素temp arr[end 1],从已排序的元素序列从后…...

go Session的实现(一)
〇、前言 众所周知,http协议是无状态的,这对于服务器确认是哪一个客户端在发请求是不可能的,因此为了能确认到,通常方法是让客户端发送请求时带上身份信息。容易想到的方法就是客户端在提交信息时,带上自己的账户和密…...

QTableView合并单元格
QtableView的功能 QTableView是Qt框架提供的用于显示表格数据的类。它是基于MVC(模型-视图-控制器)设计模式的一部分,用于将数据模型和界面视图分离。 以下是一些QTableView的主要特点和功能: 1. 显示表格数据: QTa…...
如何使用SpringCloud Eureka 创建单机Eureka Server-注册中心
😀前言 本篇博文是关于使用SpringCloud Eureka 创建单机Eureka Server-注册中心,希望你能够喜欢 🏠个人主页:晨犀主页 🧑个人简介:大家好,我是晨犀,希望我的文章可以帮助到大家&…...

QT连接OpenCV库实现人脸识别
一、关于图像处理的相关类和函数 图像容器:Mat类 读取图像: Mat imread( const String& filename, int flags IMREAD_COLOR ); 功能:读取出图像 参数:图像路径 返回值:读取的图像 命名展示图像的窗口ÿ…...
基于SSM+Vue的网上花店系统
末尾获取源码 开发语言:Java Java开发工具:JDK1.8 后端框架:SSM 前端:采用Vue技术开发 数据库:MySQL5.7和Navicat管理工具结合 服务器:Tomcat8.5 开发软件:IDEA / Eclipse 是否Maven项目&#x…...

两种解法解决 LeetCode 27. 移除元素【C++】
移除元素 27. 移除元素题目:[移除元素](https://leetcode.cn/problems/remove-element/description/)示例和提示:解法:1. 暴力解法 2. 快慢指针 27. 移除元素 题目:移除元素 示例和提示: 解法: 1. 暴力解…...
Vue + Element UI 前端篇(七):功能组件封装
组件封装 为了避免组件代码的臃肿,这里对主要的功能部件进行封装,保证代码的模块化和简洁度。 组件结构 组件封装重构后,试图组件结构如下图所示 代码一览 Home组件被简化,包含导航、头部和主内容三个组件。 Home.vue <te…...

QT QToolBox控件使用详解
本文详细的介绍了QToolBox控件的各种操作,例如:新建界面、添加页签、索引设置当前项、获取当前项的索引、获取当前项窗口、获取索引值是int的窗口、移除索引值项、获取项的数量、获取指定索引值、设置索引项是否激活、获取索引值项是否激活、设置项的图标…...
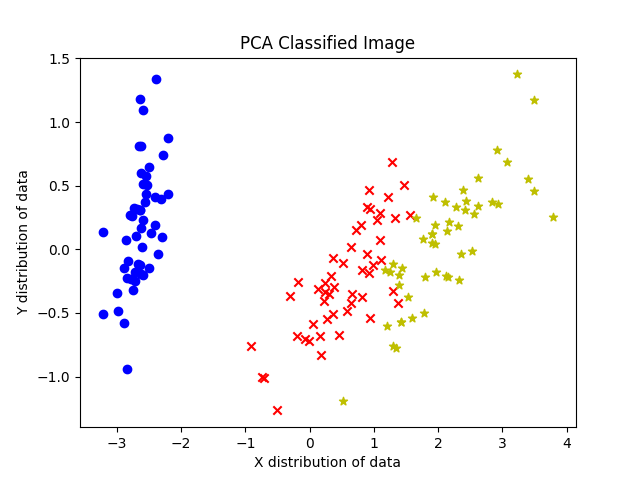
数学建模--主成分分析法(PCA)的Python实现(
目录 1.算法核心思想: 2.算法核心代码: 3.算法分类效果: 1.算法核心思想: 1.设置降维后主成分的数目为2 2.进行数据降维 3.设置main_factors1个划分类型 4.根据组分中的值进行分类 5.绘制出对应的图像 2.算法核心代码:…...

【数据结构篇】线性表2 —— 栈和队列
前言:上一篇我们介绍了顺序表和链表 (https://blog.csdn.net/iiiiiihuang/article/details/132615465?spm1001.2014.3001.5501), 这一篇我们将介绍栈和队列,栈和队列都是基于顺序表和链表来实现的 目录 栈ÿ…...

万物互联:软件与硬件的协同之道
在当今数字化时代,我们身边的一切似乎都与计算机和互联网有关。从智能手机到智能家居设备,从自动驾驶汽车到工业生产线,无论我们走到哪里,都能看到软件和硬件的协同作用。本文将探讨这种协同作用,解释软件和硬件如何相…...

ping: www.baidu.com: Name or service not known 写了DNS还是不行
环境描述:ESXI平台上,一台Centos7虚拟主机。 问题描述:平台上的其他的虚拟机可以正常ping通,就这台ping IP地址可以通,ping域名解析失败。 排查过程: 1、检查网卡配置文件和/etc/resolv.conf配置文件是否…...

C++中的decltype、std::declval 和 std::decay_t傻傻分不清楚
文章目录 前言它们是什么通俗解释总结 前言 在C中提到推导第一个映入脑海的可能是“模板”,当然有人也可能想到 auto,这些都是和推导相关的语言语法,再比如“完美转发”等等,总是就是他们的类型不用明明白白的写出来,…...

什么是Ubuntu LTS?与常规版本的区别
Ubuntu LTS(Long-Term Support)是Ubuntu操作系统的一个特殊版本,旨在提供更长时间的支持和稳定性。与常规的Ubuntu版本相比,LTS版本在以下几个方面有所不同: 支持周期更长: 使用Ubuntu LTS版本,…...

如何写一个可以找到工作的简历不至于太烂
简历是自己的一个很重要的标签,是获得面试的敲门砖,简历是要时常更新的,否则会错过一些机会。简历也是给自己的正反馈。 方法 ● 模仿,例如Boss,拉钩下面都给你一个案例模板供你参考,但是我觉得其实参考性…...

el-select 使用
案例: /* * label : 界面上展示的是哪个字段,我这里需要展示名称 * value : 绑定的字段,一般是id */<el-selectv-model"Form.BillNumber"placeholder"请选择"change"changeValue($event)"><el-optionv-for"…...

思维导图怎么变成ppt?4个思维导图一键生成ppt的方法
做好的思维导图如何变成一份ppt?本文罗列了4个可行方法,一起来看看吧。 一 直接复制粘贴 这是最简单的方法,虽然这样可能会花费一些时间,但可以确保内容排版和布局与你想要的一致。当然,我们大可使用更高效的方法。…...

3D点云处理:点云投影为2D图像 调平点云(附源码)
文章目录 0. 测试效果1. 基本内容1.1 计算点云位姿1.2 调平点云1.3 点云投影2. 代码实现文章目录:3D视觉个人学习目录微信:dhlddxB站: Non-Stop_0. 测试效果...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

基于数字孪生的水厂可视化平台建设:架构与实践
分享大纲: 1、数字孪生水厂可视化平台建设背景 2、数字孪生水厂可视化平台建设架构 3、数字孪生水厂可视化平台建设成效 近几年,数字孪生水厂的建设开展的如火如荼。作为提升水厂管理效率、优化资源的调度手段,基于数字孪生的水厂可视化平台的…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

Java 加密常用的各种算法及其选择
在数字化时代,数据安全至关重要,Java 作为广泛应用的编程语言,提供了丰富的加密算法来保障数据的保密性、完整性和真实性。了解这些常用加密算法及其适用场景,有助于开发者在不同的业务需求中做出正确的选择。 一、对称加密算法…...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

全面解析各类VPN技术:GRE、IPsec、L2TP、SSL与MPLS VPN对比
目录 引言 VPN技术概述 GRE VPN 3.1 GRE封装结构 3.2 GRE的应用场景 GRE over IPsec 4.1 GRE over IPsec封装结构 4.2 为什么使用GRE over IPsec? IPsec VPN 5.1 IPsec传输模式(Transport Mode) 5.2 IPsec隧道模式(Tunne…...

C语言中提供的第三方库之哈希表实现
一. 简介 前面一篇文章简单学习了C语言中第三方库(uthash库)提供对哈希表的操作,文章如下: C语言中提供的第三方库uthash常用接口-CSDN博客 本文简单学习一下第三方库 uthash库对哈希表的操作。 二. uthash库哈希表操作示例 u…...
