【算法】快速排序 详解
快速排序 详解
- 快速排序
- 1. 挖坑法
- 2. 左右指针法 (Hoare 法)
- 3. 前后指针法
- 4. 快排非递归
- 代码优化
排序: 排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
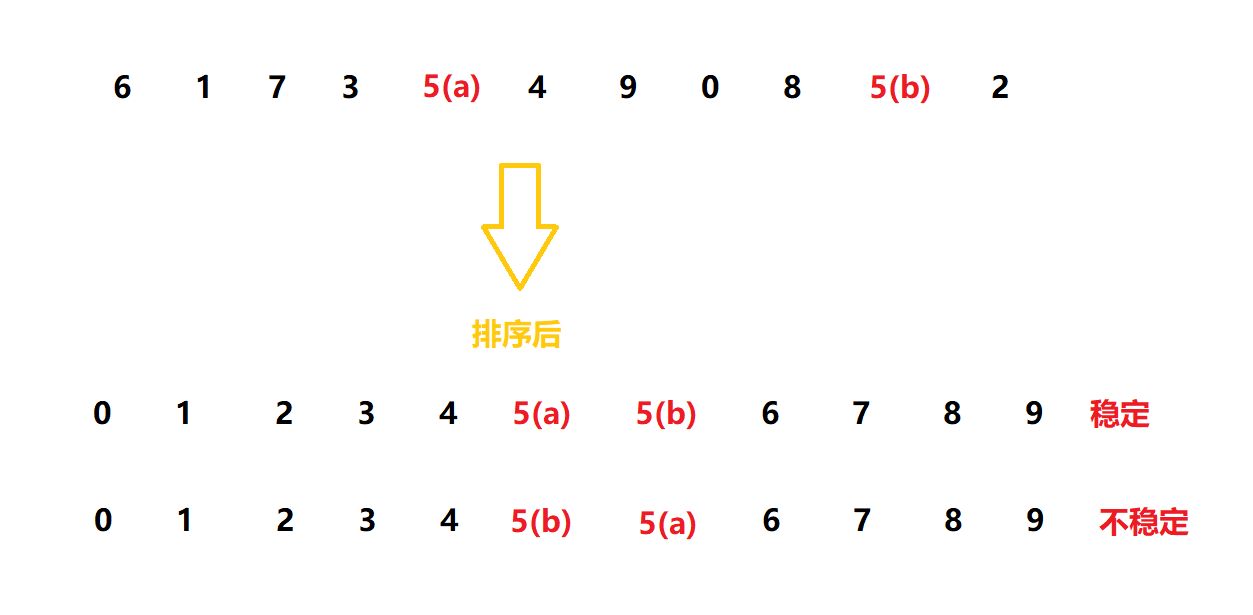
稳定性: 假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中, r[i] = r[j], 且 r[i] 在 r[j] 之前,而在排序后的序列中, r[i] 仍在 r[j] 之前,则称这种排序算法是稳定的;否则称为不稳定的。
(注意稳定排序可以实现为不稳定的形式, 而不稳定的排序实现不了稳定的形式)
内部排序: 数据元素全部放在内存中的排序。
外部排序: 数据元素太多不能同时放在内存中,根据排序过程的要求不能在内外存之间移动数据的排序。
快速排序
快速排序是 Hoare 于 1962 年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止。
1. 挖坑法
-
选择基准元素:从待排序的数组中选择一个元素作为基准(pivot)。通常情况下,可以选择第一个元素、最后一个元素、中间元素或者随机选择一个元素作为基准。
-
分割数组:从数组的两端开始,分别设置两个指针,一个从左边(low指针)开始,一个从右边(high指针)开始,分别向中间移动,直到它们相遇。在移动过程中,通过比较元素与基准的大小关系,找到一个大于基准的元素和一个小于基准的元素,并将它们互换位置。
-
继续分割:重复步骤2,直到low指针和high指针相遇。在此过程中,将小于基准的元素移到基准的左侧,将大于基准的元素移到基准的右侧,形成三个区域。
-
递归排序:对左侧小于基准的区域和右侧大于基准的区域,分别递归地应用快速排序算法。
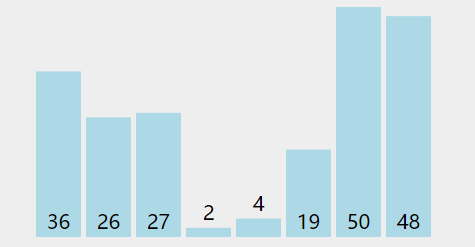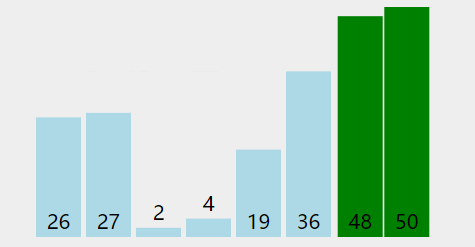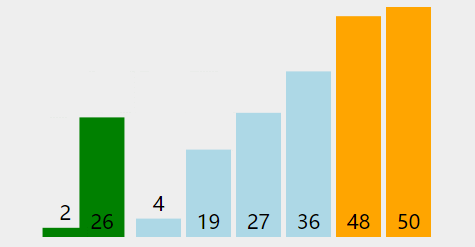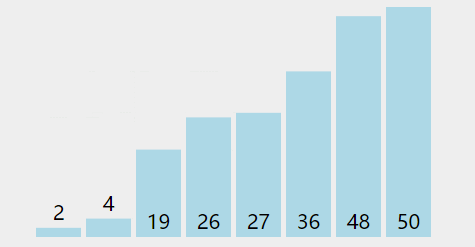
public static void quickSort(int[] arr) {int len = arr.length;partition(arr, 0, len-1);}public static void partition(int[] arr, int left, int right) {if (left >= right) {return;}int pivot = left;int value = arr[left];// 从两边开始遍历int begin = left;int end = right;while (begin < end) {// 注意一定要带上 ==, 不然死循环while (begin < end && arr[end] >= value) {end--;}// 右边找到小于 value 的值arr[pivot] = arr[end];// end 变为 坑pivot = end;while (begin < end && arr[begin] <= value) {begin++;}// 左边找到大于 value 的值arr[pivot] = arr[begin];// begin 变为坑pivot = begin;}// value 找到自己的正确位置arr[pivot] = value;// 递归左边和右边partition(arr, left, pivot-1);partition(arr, pivot+1, right);}
2. 左右指针法 (Hoare 法)
从两边开始, 左边找到比基准值大的, 右边找比基准值小的, 找到后, 两边交换, 一直到左右两个指针相遇, 相遇位置即为基准值的正确位置, 然后递归确定左右两边的区间元素的位置。
public static void quickSort(int[] arr) {int len = arr.length;partition(arr, 0, len-1);}public static void partition(int[] arr, int left, int right) {if (left >= right) {return;}int value = arr[left];int begin = left;int end = right;while (begin < end) {// 注意一定要带上 ==, 不然死循环while (begin < end && arr[end] >= value) {end--;}while (begin < end && arr[begin] <= value) {begin++;}swap(arr, begin, end);}swap(arr, left, begin);partition(arr, left, begin-1);partition(arr, begin+1, right);}public static void swap (int[] arr, int index1, int index2) {int temp = arr[index1];arr[index1] = arr[index2];arr[index2] = temp;}
3. 前后指针法
后面的指针指向小于基准值的最后一个, 前面的指针一直往后找, 找到小于基准值的就与后面指针的下一个位置交换, 后面的指针 ++, 直到前面的指针遍历完, 最后后面的指针的位置, 就是基准值的正确位置。然后再递归确定左右区间的元素的位置。
public static void quickSort(int[] arr) {int len = arr.length;partition(arr, 0, len-1);}public static void partition(int[] arr, int left, int right) {if (left >= right) {return;}int value = arr[left];// 前后指针int end = left;int front = left + 1;while (front <= right) {if (arr[front] < value) {swap(arr, end+1, front);end++;}front++;}swap(arr, left, end);// 递归左边和右边partition(arr, left, end-1);partition(arr, end+1, right);}public static void swap (int[] arr, int index1, int index2) {int temp = arr[index1];arr[index1] = arr[index2];arr[index2] = temp;}
4. 快排非递归
使用栈记录要排序的区间
public static void quickSortNonR(int[] arr) {int len = arr.length;Stack<Integer> stack = new Stack<>();stack.push(arr.length-1);stack.push(0);while (!stack.isEmpty()) {int left = stack.pop();int right = stack.pop();if (left >= right) {continue;}int pivot = left;int value = arr[left];// 从两边开始遍历int begin = left;int end = right;while (begin < end) {// 注意一定要带上 ==, 不然死循环while (begin < end && arr[end] >= value) {end--;}// 右边找到小于 value 的值arr[pivot] = arr[end];// end 变为 坑pivot = end;while (begin < end && arr[begin] <= value) {begin++;}// 左边找到大于 value 的值arr[pivot] = arr[begin];// begin 变为坑pivot = begin;}// value 找到自己的正确位置arr[pivot] = value;// 右区间stack.push(right);stack.push(pivot+1);// 左区间stack.push(pivot-1);stack.push(left);}}代码优化
优化一:
三数取中:
当我们找基准值时, 基准值越靠近是中位数,每次都近似于将一个大的区间分成两个相等的区间, 那么时间复杂度越低, 越靠近是 O(N*logN), 最坏的情况下, 每次确定一个元素, 即分成的两个区间其中一个只有一个元素, 那么如果每次都是这样的话, 最终的时间复杂度为 O(N*N), 所以选择基准值时, 越靠近中位数越好。
这里面以前后指针为例使用了 三数取中
public static void quickSort(int[] arr) {int len = arr.length;partition(arr, 0, len-1);}/*** 前后指针*/public static void partition(int[] arr, int left, int right) {if (left >= right) {return;}// 三数取中int midIndex = getMidIndex(arr, left, right);swap(arr, left, midIndex);int value = arr[left];// 前后指针int end = left;int front = left + 1;while (front <= right) {if (arr[front] < value) {swap(arr, end+1, front);end++;}front++;}swap(arr, left, end);// 递归左边和右边partition(arr, left, end-1);partition(arr, end+1, right);}public static int getMidIndex(int[] arr, int left, int right) {int midIndex = ((right - left) >> 1) + left;if (arr[left] <= arr[midIndex]) {if (arr[midIndex] <= arr[right]) {return midIndex;} else {if (arr[left] >= arr[right]) {return left;} else {return right;}}} else {if (arr[midIndex] >= arr[right]) {return midIndex;} else {if (arr[left] >= arr[right]) {return right;} else {return left;}}}}public static void swap (int[] arr, int index1, int index2) {int temp = arr[index1];arr[index1] = arr[index2];arr[index2] = temp;}
优化二:
小区间优化, 当区间中元素数量比较少时,区间中元素本身就接近有序, 使用直接插入排序能提高效率 (直接插入排序)
假如说有 100W 个数据, 就会调用 100W 次 partition 函数, 但是光最后两层就会调用近 80W 次, 所以使用小区间优化提高效率。
直接插入排序
public static void insertSort(int[] arr) {int len = arr.length;for (int i = 1; i < len; i++) {// 从已经有序的位置从后往前开始比较int key = arr[i];int end = i-1;while (end >= 0 && arr[end] > key) {// 数据往后挪arr[end+1] = arr[end];end--;}// 找到了合适位置, 就插入进去arr[end+1] = key;}}
在快排中使用小区间优化
/*** 直接插入排序*/public static void insertSort(int[] arr, int left, int right) {for (int i = left+1; i <= right; i++) {// 从已经有序的位置从后往前开始比较int key = arr[i];int end = i-1;while (end >= 0 && arr[end] > key) {// 数据往后挪arr[end+1] = arr[end];end--;}// 找到了合适位置, 就插入进去arr[end+1] = key;}}public static void quickSort(int[] arr) {int len = arr.length;partition(arr, 0, len-1);}public static void partition(int[] arr, int left, int right) {if (left >= right) {return;}// 小区间优化, 当数组中元素个数 <= 100 个时使用直接插入排序// 主要是减少了递归的次数if (right - left + 1 <= 100) {insertSort(arr, left, right);return;}// 三数取中int midIndex = getMidIndex(arr, left, right);swap(arr, left, midIndex);int value = arr[left];// 前后指针int end = left;int front = left + 1;while (front <= right) {if (arr[front] < value) {swap(arr, end+1, front);end++;}front++;}swap(arr, left, end);// 递归左边和右边partition(arr, left, end-1);partition(arr, end+1, right);}总结:
- 快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
- 时间复杂度: O (N*logN)
- 空间复杂度: O(logN)
- 是不稳定排序
- 对数据比较敏感: 当数据本身就是有序时, 情况最坏, 因为每次只能确定一个数据, 时间复杂度为 O(N*N)
好啦, 以上就是对快速排序的讲解, 希望能帮到你 !
评论区欢迎指正 !
相关文章:

【算法】快速排序 详解
快速排序 详解 快速排序1. 挖坑法2. 左右指针法 (Hoare 法)3. 前后指针法4. 快排非递归 代码优化 排序: 排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。 稳定性&…...

架构师spring boot 面试题
spring boot 微服务有哪些特点? Spring Boot 微服务具有以下特点: 独立性:每个微服务都是独立的部署单元,有自己的代码库和数据库。这使得微服务可以独立开发、测试、部署和扩展。 分布式:微服务架构将一个大型应用程…...

电商系统架构设计系列(十一):在电商的交易类系统中,如何正确地使用 Redis 这样的缓存系统呢?需要考虑哪些问题?
上篇文章中,我给你留了一个思考题:在电商的交易类系统中,如何正确地使用 Redis 这样的缓存系统呢?需要考虑哪些问题? 这篇文章,我们来聊聊。 引言 我们知道,大部分面向公众用户的互联网系统&a…...

MySQL数据库和表的操作
数据库基础 存储数据用文件就可以了,为什么还要弄个数据库? 文件保存数据有以下几个缺点: 1、文件的安全性问题 2、文件不利于数据查询和管理 3、文件不利于存储海量数据 4、文件在程序中控制不方便 数据库存储介质: 磁盘 内存 为了解决上…...
DAY-01--分布式微服务基础概念
一、项目简介 了解整体项目包含后端、前端、周边维护。整个项目的框架知识。 二、分布式基础概念 1、微服务 将应用程序 基于业务 拆分为 多个小服务,各小服务单独部署运行,采用http通信。 2、集群&分布式&节点 集群是个物理形态,…...

记:一次关于paddlenlp、python、版本之间的兼容性问题
兼容版本 Python 3.10.8 absl-py1.4.0 accelerate0.19.0 addict2.4.0 aiofiles23.1.0 aiohttp3.8.3 aiosignal1.3.1 alembic1.10.4 aliyun-python-sdk-core2.13.36 aliyun-python-sdk-kms2.16.0 altair4.2.2 altgraph0.17.3 aniso86019.0.1 antlr4-python3-runtime4.9.3 anyi…...

MyBatis配置及单表操作
文章目录 一. MyBatis概述二. MyBatis项目的创建1. 准备一个数据表2. 创建项目 三. MyBatis的使用1. 基本使用2. SpringBoot单元测试 四. 使用MyBatis实现单表操作1. 查询2. 修改3. 删除4. 新增 五. 基于注解完成SQL 一. MyBatis概述 MyBatis 是一款优秀的持久层框架ÿ…...

python基础教程:深浅copy的详细用法
前言 嗨喽,大家好呀~这里是爱看美女的茜茜呐 1.先看赋值运算 l1 [1,2,3,[barry,alex]] l2 l1l1[0] 111 print(l1) # [111, 2, 3, [barry, alex]] print(l2) # [111, 2, 3, [barry, alex]]l1[3][0] wusir print(l1) # [111, 2, 3, [wusir, alex]] print(l2)…...
【算法篇】动态规划(二)
文章目录 分割回文字符串编辑距离不同的子序列动态规划解题思路 分割回文字符串 class Solution { public:bool isPal(string& s,int begin,int end){while(begin<end){if(s[begin]!s[end]){return false;}begin;end--;}return true;}int minCut(string s) {int lens.si…...
数据库 SQL高级查询语句:聚合查询,多表查询,连接查询
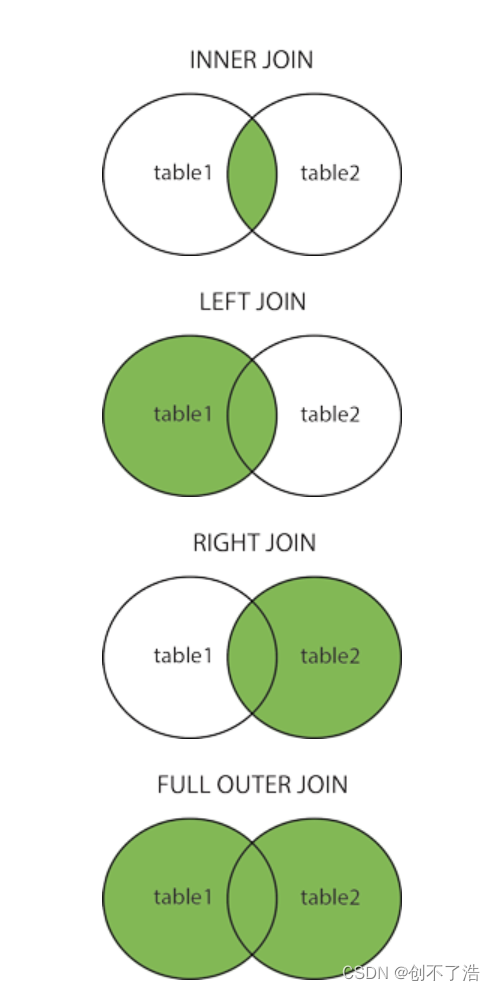
目录 创建学生表聚合查询聚合函数直接查询设置别名查询设置条件查询 常用的聚合函数 分组查询单个字段Group by报错分组查询多字段分组查询 多表查询直接查询重命名查询Students表新建一列CourseID 连接(JOIN)查询INNER JOINRIGHT JOIN, LEFT JOINFULL J…...

pytorch-构建卷积神经网络
构建卷积神经网络 卷积网络中的输入和层与传统神经网络有些区别,需重新设计,训练模块基本一致 import torch import torch.nn as nn import torch.optim as optim import torch.nn.functional as F from torchvision import datasets,transforms impor…...
)
点云从入门到精通技术详解100篇-点云滤波算法及单木信息提取(续)
目录 3.3 点云滤波算法原理概述 3.3.1 坡度滤波算法 3.3.2 基于不规则三角网滤波 3.3.3 数学形态学滤波...

Gartner发布中国科技报告:数据编织和大模型技术崭露头角
近日,全球知名科技研究和咨询机构Gartner发布了关于中国数据分析与人工智能技术的最新报告。报告指出,中国正迎来数据分析与人工智能领域的蓬勃发展,预计到2026年,将有超过30%的白领工作岗位重新定义,生成式人工智能技…...

java八股文面试[数据库]——explain
使用 EXPLAIN 关键字可以模拟优化器来执行SQL查询语句,从而知道MySQL是如何处理我们的SQL语句的。分析出查询语句或是表结构的性能瓶颈。 MySQL查询过程 通过explain我们可以获得以下信息: 表的读取顺序 数据读取操作的操作类型 哪些索引可以被使用 …...

Kafka3.0.0版本——增加副本因子
目录 一、服务器信息二、启动zookeeper和kafka集群2.1、先启动zookeeper集群2.2、再启动kafka集群 三、增加副本因子3.1、增加副本因子的概述3.2、增加副本因子的示例3.2.1、创建topic(主题)3.2.2、手动增加副本存储 一、服务器信息 四台服务器 原始服务器名称原始服务器ip节点…...
升级iOS 17出现白苹果、不断重启等系统问题怎么办?
iOS 17发布后了,很多果粉都迫不及待的将iphone/ipad升级到最新iOS17系统,体验新系统功能。 但部分果粉因硬件、软件的各种情况,导致升级系统后出现故障,比如白苹果、不断重启、卡在系统升级界面等等问题。 如果遇到了这些系统问题…...

6. `Java` 并发基础之`ReentrantReadLock`
前言:随着多线程程序的普及,线程同步的问题变得越来越常见。Java中提供了多种同步机制来确保线程安全,其中之一就是ReentrantLock。ReentrantLock是Java中比较常用的一种同步机制,它提供了一系列比synchronized更加灵活和可控的操…...
float浮动布局大战position定位布局
华子目录 布局方式普通文档流布局浮动布局(浮动主要针对与black,inline元素)float属性浮动用途浮动元素父级高度塌陷 position属性定位篇相对定位(relative为属性值,配合left属性,和top属性使用)…...
算法 数据结构 递归插入排序 java插入排序 递归求解插入排序算法 如何用递归写插入排序 插入排序动图 插入排序优化 数据结构(十)
1. 插入排序(insertion-sort): 是一种简单直观的排序算法。它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入 算法稳定性: 对于两个相同的数,经过…...
OpenCV(二十二):均值滤波、方框滤波和高斯滤波
目录 1.均值滤波 2.方框滤波 3.高斯滤波 1.均值滤波 OpenCV中的均值滤波(Mean Filter)是一种简单的滤波技术,用于平滑图像并减少噪声。它的原理非常简单:对于每个像素,将其与其周围邻域内像素的平均值作为新的像素值…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

电脑插入多块移动硬盘后经常出现卡顿和蓝屏
当电脑在插入多块移动硬盘后频繁出现卡顿和蓝屏问题时,可能涉及硬件资源冲突、驱动兼容性、供电不足或系统设置等多方面原因。以下是逐步排查和解决方案: 1. 检查电源供电问题 问题原因:多块移动硬盘同时运行可能导致USB接口供电不足&#x…...

家政维修平台实战20:权限设计
目录 1 获取工人信息2 搭建工人入口3 权限判断总结 目前我们已经搭建好了基础的用户体系,主要是分成几个表,用户表我们是记录用户的基础信息,包括手机、昵称、头像。而工人和员工各有各的表。那么就有一个问题,不同的角色…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...

论文浅尝 | 基于判别指令微调生成式大语言模型的知识图谱补全方法(ISWC2024)
笔记整理:刘治强,浙江大学硕士生,研究方向为知识图谱表示学习,大语言模型 论文链接:http://arxiv.org/abs/2407.16127 发表会议:ISWC 2024 1. 动机 传统的知识图谱补全(KGC)模型通过…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

NLP学习路线图(二十三):长短期记忆网络(LSTM)
在自然语言处理(NLP)领域,我们时刻面临着处理序列数据的核心挑战。无论是理解句子的结构、分析文本的情感,还是实现语言的翻译,都需要模型能够捕捉词语之间依时序产生的复杂依赖关系。传统的神经网络结构在处理这种序列依赖时显得力不从心,而循环神经网络(RNN) 曾被视为…...

Java面试专项一-准备篇
一、企业简历筛选规则 一般企业的简历筛选流程:首先由HR先筛选一部分简历后,在将简历给到对应的项目负责人后再进行下一步的操作。 HR如何筛选简历 例如:Boss直聘(招聘方平台) 直接按照条件进行筛选 例如:…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...
