《机器人学一(Robotics(1))》_台大林沛群 第 5 周【机械手臂 轨迹规划】 Quiz 5
我又行了!🤣
求解的 位置 可能会有 变动,根据求得的A填写相应值即可。注意看题目。
coursera链接
文章目录
- 第1题 Cartesian space
- 求解 题1-3 的 Python 代码
- 第2题
- 第3题
- 第4题 Joint space
- 求解 题4-6 的 Python 代码
- 第5题
- 第6题
- 其它可参考代码 Python
笛卡尔空间:




第1题 Cartesian space

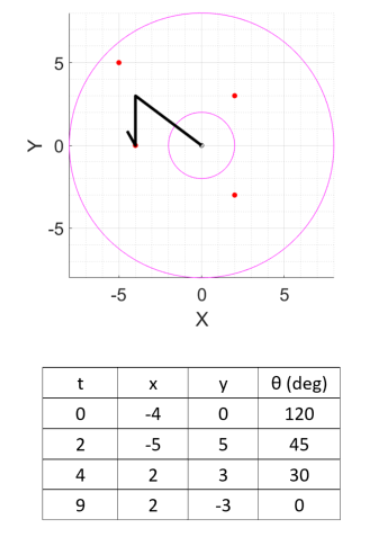


求解 题1-3 的 Python 代码
import numpy as np Δt1 = 2 - 0
Δt2 = 4 - 2
Δt3 = 9 - 4T = [[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],[1, Δt1, Δt1**2, Δt1**3, 0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 1, Δt2, Δt2**2, Δt2**3, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0, 1, Δt3, Δt3**2, Δt3**3],[0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 2*Δt3, 3*Δt3**2],[0, 1, 2*Δt1, 3*Δt1**2, 0, -1, 0, 0, 0, 0, 0, 0],[0, 0, 2, 6*Δt1, 0, 0, -2, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 1, 2*Δt2, 3*Δt2**2, 0, -1, 0, 0],[0, 0, 0, 0, 0, 0, 2, 6*Δt2, 0, 0, -2, 0] ] ## 需要仔细 检查, 很容易 打错def getA(θ):θ = np.array(θ)A = np.dot(np.linalg.inv(T), θ.T)A = np.around(A, decimals = 2) ## 结果 保留 到 小数点 后 两位return A ## X 的导数 为 速度, 初始和末尾的速度均为0
X = [-4, -5, -5, 2, 2, 2, 0, 0, 0, 0, 0, 0]
print('X_A:')
print(getA(X))## Y 的导数 为 速度, 初始和末尾的速度均为0
Y = [0, 5, 5, 3, 3, -3, 0, 0, 0, 0, 0, 0]
print('\nY_A:')
print(getA(Y))## θ
θ = [120, 45, 45, 30, 30, 0, 0, 0, 0, 0, 0, 0]
print('\nθ_A:')
print(getA(θ))
矩阵合并版本:
import numpy as np np.set_printoptions(suppress = True)Δt1 = 2 - 0
Δt2 = 4 - 2
Δt3 = 9 - 4T = [[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],[1, Δt1, Δt1**2, Δt1**3, 0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 1, Δt2, Δt2**2, Δt2**3, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0, 1, Δt3, Δt3**2, Δt3**3],[0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 2*Δt3, 3*Δt3**2],[0, 1, 2*Δt1, 3*Δt1**2, 0, -1, 0, 0, 0, 0, 0, 0],[0, 0, 2, 6*Δt1, 0, 0, -2, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 1, 2*Δt2, 3*Δt2**2, 0, -1, 0, 0],[0, 0, 0, 0, 0, 0, 2, 6*Δt2, 0, 0, -2, 0] ]def getA(Θ): ## 这里 直接使用矩阵 A = np.dot(np.linalg.inv(T), Θ)A = np.around(A, decimals = 2) ## 结果 保留 到 小数点 后 两位return A Θ = [[-4, 0, 120],[-5, 5, 45],[-5, 5, 45],[2, 3, 30],[2, 3, 30],[2, -3, 0],[0, 0, 0], [0, 0, 0], [0, 0, 0], [0, 0, 0], [0, 0, 0], [0, 0, 0]]
print('A:')
print(getA(Θ))
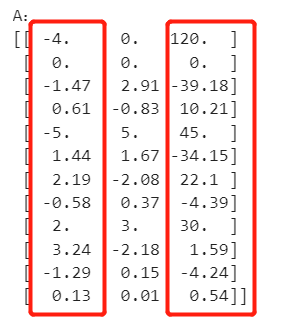
第1题答案: -5//1.44//2.19//-0.58
第2题

第2题答案: 5//1.67//-2.08//0.37
第3题

第3题答案: 120//0//-39.18//10.21
第4题 Joint space

根据这个,需要求解 每个 位姿下的 (θ1,θ2,θ3)

第4周的PPT:
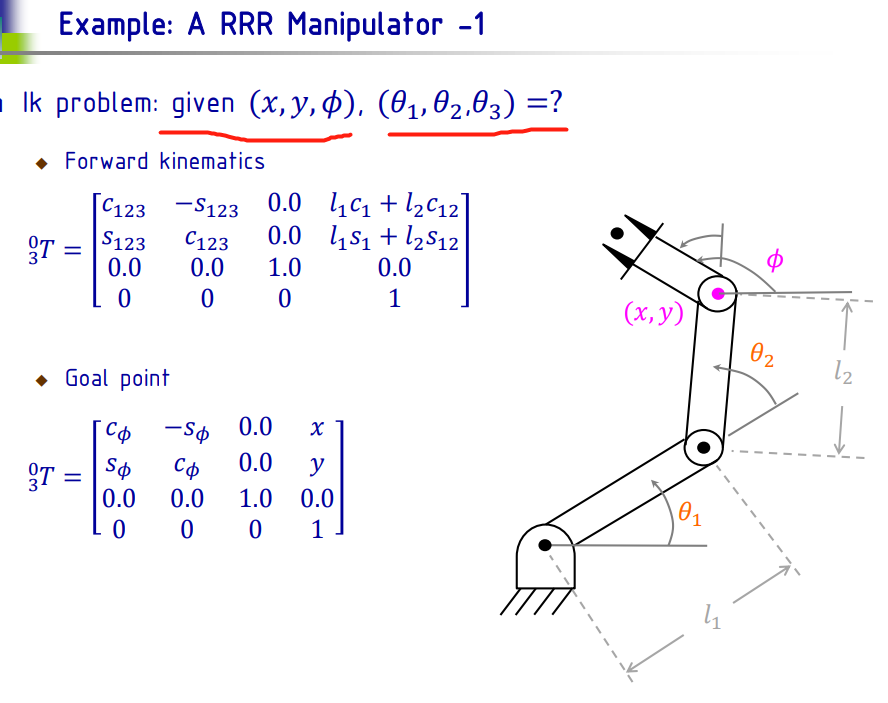
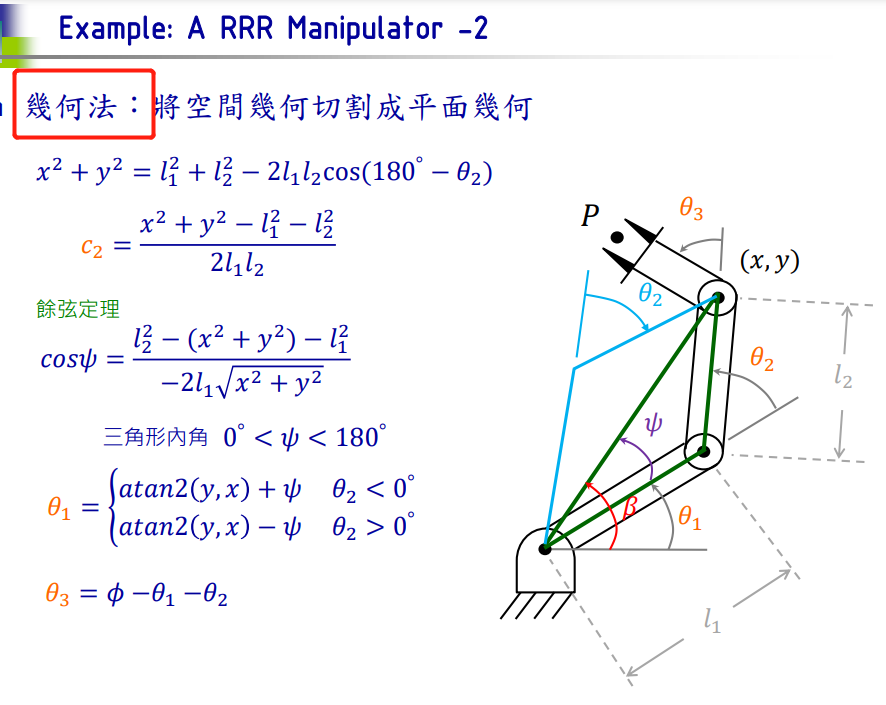


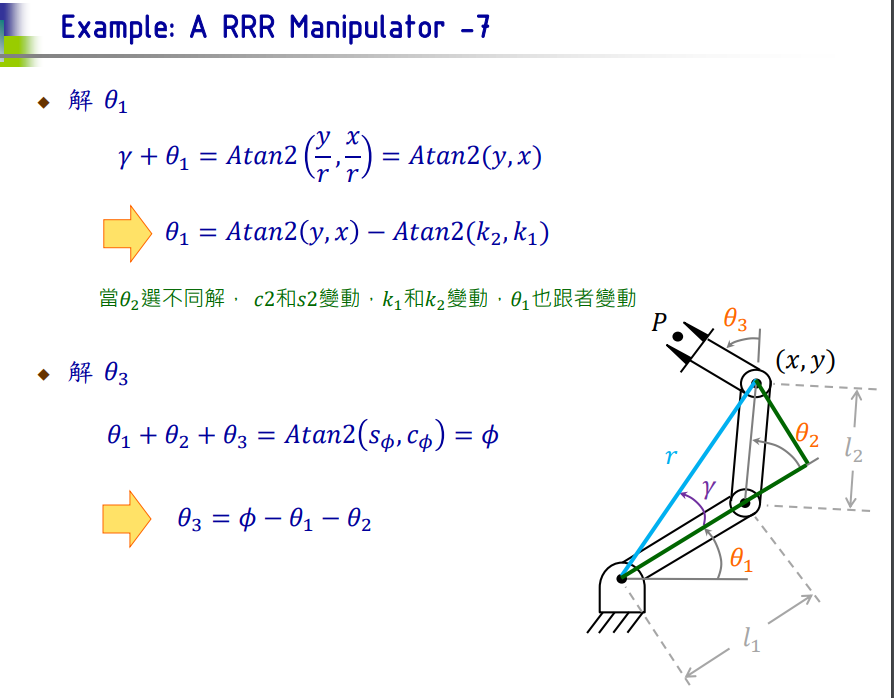
求解 题4-6 的 Python 代码
### 已知 (x, y, θ),求解 (θ1, θ2, θ3)
import numpy as np
import math ## atan2(y, x, /)### 获取 等号左边的 [θ1, θ2, θ3] 矩阵
l1 = 5
l2 = 3
l3 = 1### 方法一: 通过几何法 求解
def RRR_geometric(x, y, θ): θ2 = np.arccos((x**2 + y**2 - l1**2 - l2**2)/(2*l1*l2))ψ = np.arccos((l2**2 - x**2 - y**2 - l1**2)/(-2 * l1 * np.sqrt(x**2 + y**2))) if θ2 < 0:θ1 = math.atan2(y, x) + ψ ## np.arctan2(y,x) 也可else:θ1 = math.atan2(y, x) - ψθ = np.pi * θ / 180 ## 角度 换 弧度θ3 = θ - θ1 - θ2return [θ1, θ2, θ3]### 方法二: 代数解
def RRR_algebraic(x, y, θ):θ2 = np.arccos((x**2 + y**2 - l1**2 - l2**2)/(2*l1*l2))k1 = l1 + l2 * np.cos(θ2)k2 = l2 * np.sin(θ2)θ1 = math.atan2(y, x) - math.atan2(k2, k1) ## np.arctan2(y,x) 也可θ = np.pi * θ / 180 ## 角度 换 弧度θ3 = θ - θ1 - θ2return [θ1, θ2, θ3]x0, y0, θ0 = -4, 0, 120
x1, y1, θ1 = -5, 5, 45
x2, y2, θ2 = 2, 3, 30
xf, yf, θf = 2, -3, 0## 选择其中一种方法计算 即可
# 法1:几何法 代入
# θ_3col = [RRR_geometric(x0, y0, θ0),
# RRR_geometric(x1, y1, θ1),RRR_geometric(x1, y1, θ1),
# RRR_geometric(x2, y2, θ2),RRR_geometric(x2, y2, θ2),
# RRR_geometric(xf, yf, θf),
# [0, 0, 0],[0, 0, 0],[0, 0, 0],[0, 0, 0],[0, 0, 0],[0, 0, 0]] ## 注意 返回 结果那样,这里就不用中括号了
## 法2: 解析解 代入
θ_3col = [RRR_algebraic(x0, y0, θ0),RRR_algebraic(x1, y1, θ1),RRR_algebraic(x1, y1, θ1),RRR_algebraic(x2, y2, θ2),RRR_algebraic(x2, y2, θ2),RRR_algebraic(xf, yf, θf),[0, 0, 0],[0, 0, 0],[0, 0, 0],[0, 0, 0],[0, 0, 0],[0, 0, 0]]
# print(θ_3col)
#######################################################
#### 求解 A
Δt1 = 2 - 0
Δt2 = 4 - 2
Δt3 = 9 - 4T = [[1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],[1, Δt1, Δt1**2, Δt1**3, 0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 1, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 1, Δt2, Δt2**2, Δt2**3, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0, 1, Δt3, Δt3**2, Δt3**3],[0, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 2*Δt3, 3*Δt3**2],[0, 1, 2*Δt1, 3*Δt1**2, 0, -1, 0, 0, 0, 0, 0, 0],[0, 0, 2, 6*Δt1, 0, 0, -2, 0, 0, 0, 0, 0],[0, 0, 0, 0, 0, 1, 2*Δt2, 3*Δt2**2, 0, -1, 0, 0],[0, 0, 0, 0, 0, 0, 2, 6*Δt2, 0, 0, -2, 0] ]def getA(θ): ## 这里 直接使用矩阵 A = np.dot(np.linalg.inv(T), θ)A = np.around(A, decimals = 2) ## 结果 保留 到 小数点 后 两位return A print('θ_A:')
print(getA(θ_3col)) 
第4题答案: 1.99//-0.6//-0.22//0.05
第5题

第5题答案: 2.21//0//-0.83//0.27
第6题

第6题答案: -2.62//0//0.23//-0.07
其它可参考代码 Python
github链接
相关文章:

《机器人学一(Robotics(1))》_台大林沛群 第 5 周【机械手臂 轨迹规划】 Quiz 5
我又行了!🤣 求解的 位置 可能会有 变动,根据求得的A填写相应值即可。注意看题目。 coursera链接 文章目录 第1题 Cartesian space求解 题1-3 的 Python 代码 第2题第3题第4题 Joint space求解 题4-6 的 Python 代码 第5题第6题其它可参考代…...
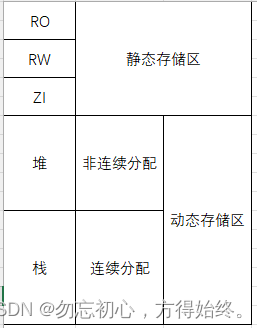
嵌入式面试/笔试C相关总结
1、存储 单片机端编译后分为code ro rw zi几个区域,其中code是执行文件,ro(read only)只读区域,存放const修饰常量、字符串。rw(read write)存放已初始化变量。zi存放未初始化变量。编译完成后bin大小为coderorw。运行时所需内存为rwzi。 在电…...

支付宝使用OceanBase的历史库实践分享
为解决因业务增长引发的数据库存储空间问题,支付宝基于 OceanBase 数据库启动了历史库项目,通过历史数据归档、过期数据清理、异常数据回滚,实现了总成本降低 80%。 历史数据归档:将在线库(SSD 磁盘)数据归…...
)
accelerate 分布式技巧(一)
accelerate分布式技巧 简单使用 Accelerate是一个来自Hugging Face的库,它简化了将单个GPU的PyTorch代码转换为单个或多台机器上的多个GPU的代码。 Accelerate精确地抽象了与多GPU/TPU/fp16相关的模板代码,并保持Pytorch其余代码不变。 import torchim…...
密码找回安全
文章目录 密码找回安全任意秘密重置 密码找回安全 用户提交修改密码请求;账号认证:服务器发送唯一ID (例如信验证码)只有账户所有者才能看的地方,完成身份验证;身份验证:用户提交验证码完成身份验证;修改密码:用户修改密码。 任意秘密重置 登录metinfo4…...

Spring Boot + Vue的网上商城之商品管理
Spring Boot Vue的网上商城之商品管理 在网上商城中,商品管理是一个非常重要的功能。它涉及到商品的添加、编辑、删除和展示等操作。本文将介绍如何使用Spring Boot和Vue来实现一个简单的商品管理系统。 下面是一个实现Spring Boot Vue的网上商城之商品管理的思路…...

B站:提高你的词汇量:如何用英语谈论驾驶
视频链接:提高你的词汇量:如何用英语谈论驾驶_哔哩哔哩_bilibili 英文音标中文hood/hʊd/n. 汽车的引擎盖go over仔细检查;认真讨论;用心思考There are plenty of videos go over this.有很多关于这个的视频unlockvt. 发现;揭开&…...

大前端面试注意要点
前端面试:从IT专家角度全面解析 在数字时代,前端开发工程师的角色变得越来越重要。随着网站和应用程序的复杂性和交互性越来越高,对具有专业技能的前端开发人员的需求也在不断增长。对于正在寻找前端开发职位的开发者,或者正在寻…...
)
稻盛和夫-如是说(读书笔记)
本书解答的核心问题: “今天,我们需要的不是短期有效的处方。作为人,何谓正确?作为人,应该如何度过人生?这才是一切问题的根源。 有几个要点和认知比较深的地方谈一谈。 1、利他 类似于阳明心学࿰…...

Jmeter是用来做什么的?
JMeter是一个开源的Java应用,主要用于性能测试和功能测试。它最初由Apache软件基金会设计用于测试Web应用程序,但现在已经扩展到其他测试功能。JMeter的主要功能如下: 性能测试:性能测试是JMeter的核心功能,主要分为两…...

Docker基础教程
Docker基础教程 Docker简介 Docker基本操作 Docker应用 Docker自定义镜像 Docker compose 为什么使用DockerDocker简介安装DockerDocker的中央仓库Docker镜像操作Docker容器操作准备一个web项目创建MySQL容器创建Tomcat容器将项目部署到TomcatDocker数据卷DockerfileDock…...

Linux命令200例:who用于显示当前登录到系统的用户信息
🏆作者简介,黑夜开发者,CSDN领军人物,全栈领域优质创作者✌。CSDN专家博主,阿里云社区专家博主,2023年6月csdn上海赛道top4。 🏆数年电商行业从业经验,历任核心研发工程师࿰…...
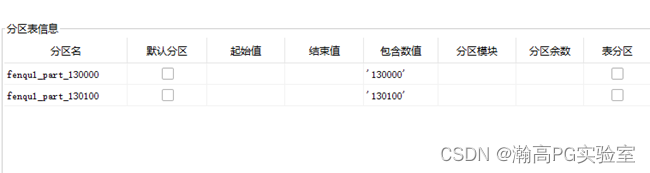
HGDB-修改分区表名称及键值
瀚高数据库 目录 环境 文档用途 详细信息 环境 系统平台:N/A 版本:4.5.7 文档用途 使用存储过程拼接SQL,修改分区名称、分区键值、并重新加入主表,适用于分区表较多场景。 详细信息 说明:本文档为测试过程࿱…...

1分钟了解音频、语音数据和自然语言处理的关系
机器学习在日常场景中的应用 音频、语音数据和自然语言处理这三者正在不断促进人工智能技术的发展,人机交互也逐渐渗透进生活的每个角落。在各行各业包括零售业、银行、食品配送服务商)的多样互动中,我们都能通过与某种形式的AI(…...
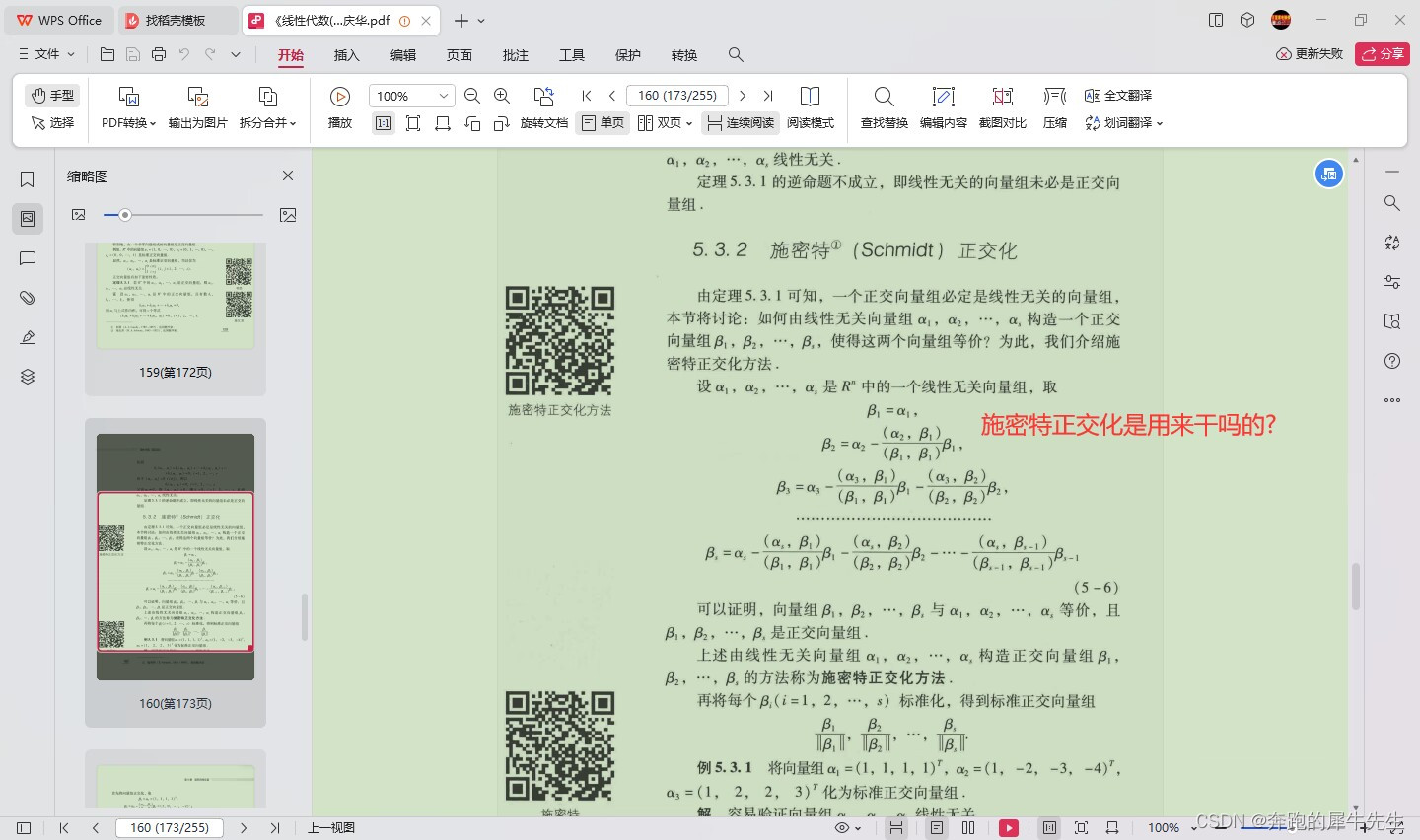
线性代数的学习和整理20,关于向量/矩阵和正交相关,相似矩阵等
目录 1 什么是正交 1.1 正交相关名词 1.2 正交的定义 1.3 正交向量 1.4 正交基 1.5 正交矩阵的特点 1.6 正交矩阵的用处 1 什么是正交 1.1 正交相关名词 orthogonal set 正交向量组正交变换orthogonal matrix 正交矩阵orthogonal basis 正交基orthogonal decompositio…...
OpenCV之ellipse函数
ellipse函数用来在图片中绘制椭圆、扇形,有两个重载函数。 函数原型1: void cv::ellipse( InputOutputArray img,Point center,Size axes,double angle,double startAngle,double …...
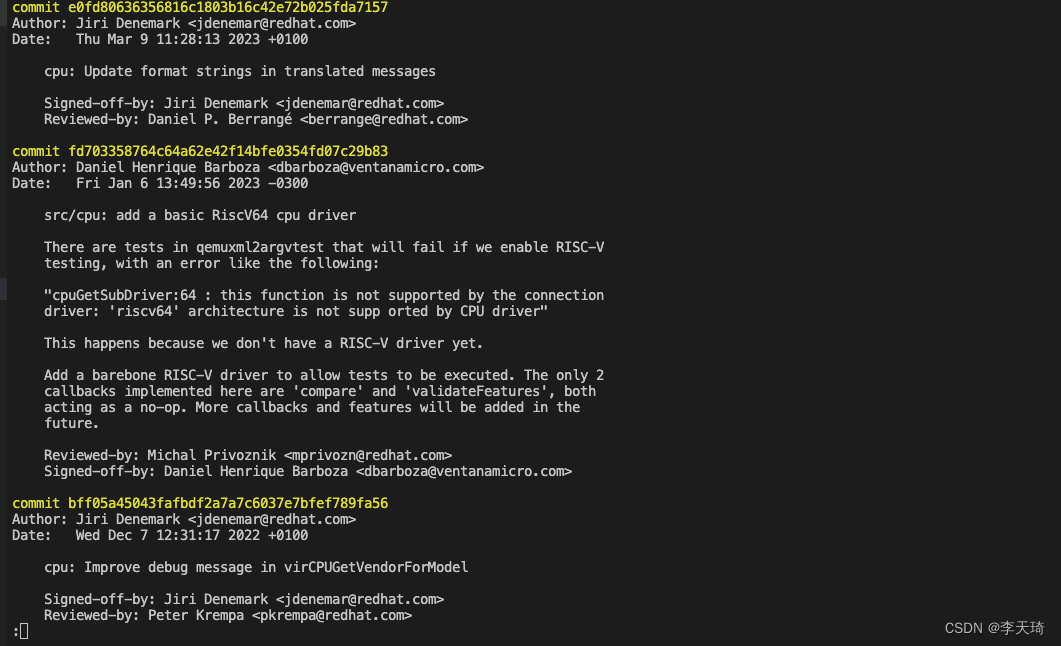
git快速查看某个文件修改的所有commit
1. git blame file git blame 可以显示历史修改的每一行记录,有时候我们只想了解某个文件一共提交几次commit,只显示commit列表,这种方式显然不满足要求。 2.git log常规使用 (1)显示整个project的所有commit (2)显示某个文件的所有commit 这是git log不添加参数的常规…...
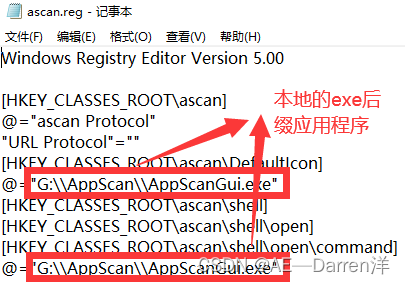
加强版python连接飞书通知——本地电脑PC端通过网页链接打开本地已安装软件(调用注册表形式,以漏洞扫描工具AppScan为例)
前言 如果你想要通过超链接来打开本地应用,那么你首先你需要将你的应用添入windows注册表中(这样网页就可以通过指定代号来调用程序),由于安全性的原因所以网页无法直接通过输入绝对路径来调用本地文件。 一、通过创建reg文件自动配置注册表 创建文本文档,使用记事本打开…...
Jmeter进阶使用指南-使用断言
Apache JMeter是一个流行的开源负载和性能测试工具。在JMeter中,断言(Assertions)是用来验证响应数据是否符合预期的一个重要组件。它是对请求响应的一种检查,如果响应不符合预期,那么断言会标记为失败。 以下是如何在…...

44、Flink之module模块介绍及使用示例和Flink SQL使用hive内置函数及自定义函数详细示例--网上有些说法好像是错误的
Flink 系列文章 1、Flink 部署、概念介绍、source、transformation、sink使用示例、四大基石介绍和示例等系列综合文章链接 13、Flink 的table api与sql的基本概念、通用api介绍及入门示例 14、Flink 的table api与sql之数据类型: 内置数据类型以及它们的属性 15、Flink 的ta…...

TDengine 快速体验(Docker 镜像方式)
简介 TDengine 可以通过安装包、Docker 镜像 及云服务快速体验 TDengine 的功能,本节首先介绍如何通过 Docker 快速体验 TDengine,然后介绍如何在 Docker 环境下体验 TDengine 的写入和查询功能。如果你不熟悉 Docker,请使用 安装包的方式快…...

K8S认证|CKS题库+答案| 11. AppArmor
目录 11. AppArmor 免费获取并激活 CKA_v1.31_模拟系统 题目 开始操作: 1)、切换集群 2)、切换节点 3)、切换到 apparmor 的目录 4)、执行 apparmor 策略模块 5)、修改 pod 文件 6)、…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

《通信之道——从微积分到 5G》读书总结
第1章 绪 论 1.1 这是一本什么样的书 通信技术,说到底就是数学。 那些最基础、最本质的部分。 1.2 什么是通信 通信 发送方 接收方 承载信息的信号 解调出其中承载的信息 信息在发送方那里被加工成信号(调制) 把信息从信号中抽取出来&am…...

JAVA后端开发——多租户
数据隔离是多租户系统中的核心概念,确保一个租户(在这个系统中可能是一个公司或一个独立的客户)的数据对其他租户是不可见的。在 RuoYi 框架(您当前项目所使用的基础框架)中,这通常是通过在数据表中增加一个…...

【生成模型】视频生成论文调研
工作清单 上游应用方向:控制、速度、时长、高动态、多主体驱动 类型工作基础模型WAN / WAN-VACE / HunyuanVideo控制条件轨迹控制ATI~镜头控制ReCamMaster~多主体驱动Phantom~音频驱动Let Them Talk: Audio-Driven Multi-Person Conversational Video Generation速…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...

快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...
