【动态规划刷题 10】等差数列划分 最长湍流子数组
413. 等差数列划分
链接: 413. 等差数列划分
如果一个数列 至少有三个元素 ,并且任意两个相邻元素之差相同,则称该数列为等差数列。
例如,[1,3,5,7,9]、[7,7,7,7] 和 [3,-1,-5,-9] 都是等差数列。
给你一个整数数组 nums ,返回数组 nums 中所有为等差数组的 子数组 个数。
子数组 是数组中的一个连续序列。
示例 1:
输入:nums = [1,2,3,4]
输出:3
解释:nums 中有三个子等差数组:[1, 2, 3]、[2, 3, 4] 和 [1,2,3,4] 自身。
示例 2:
输入:nums = [1]
输出:0
1.状态表示*
dp[i] 表⽰必须「以 i 位置的元素为结尾」的等差数列有多少种
2.状态转移方程
对于 dp[i] 位置的元素 nums[i] ,会与前⾯的两个元素有下⾯两种情况:
- i. nums[i - 2], nums[i - 1], nums[i] 三个元素不能构成等差数列:那么以 nums[i]为结尾的等差数列就不存在此时
dp[i] = 0; - ii. nums[i - 2], nums[i - 1], nums[i] 三个元素可以构成等差数列:那么以 nums[i - 1] 为结尾的所有等差数列后⾯填上⼀个 nums[i] 也是⼀个等差数列,此时 dp[i] = dp[i - 1] 。但是,因为 nums[i- 2], nums[i - 1], nums[i] 三 者⼜能构成⼀个新的等差数列,因此要在之前的基础上再添上⼀个等差数列,于是
dp[i] = dp[i - 1] + 1
3. 初始化
由于需要⽤到前两个位置的元素,但是前两个位置的元素⼜⽆法构成等差数列,因此 dp[0] =dp[1] = 0 。
4. 填表顺序
根据「状态转移⽅程」易得,填表顺序为「从左往右」
5. 返回值
因为我们要的是所有的等差数列的个数,因此需要返回整个 dp 表⾥⾯的元素之和。
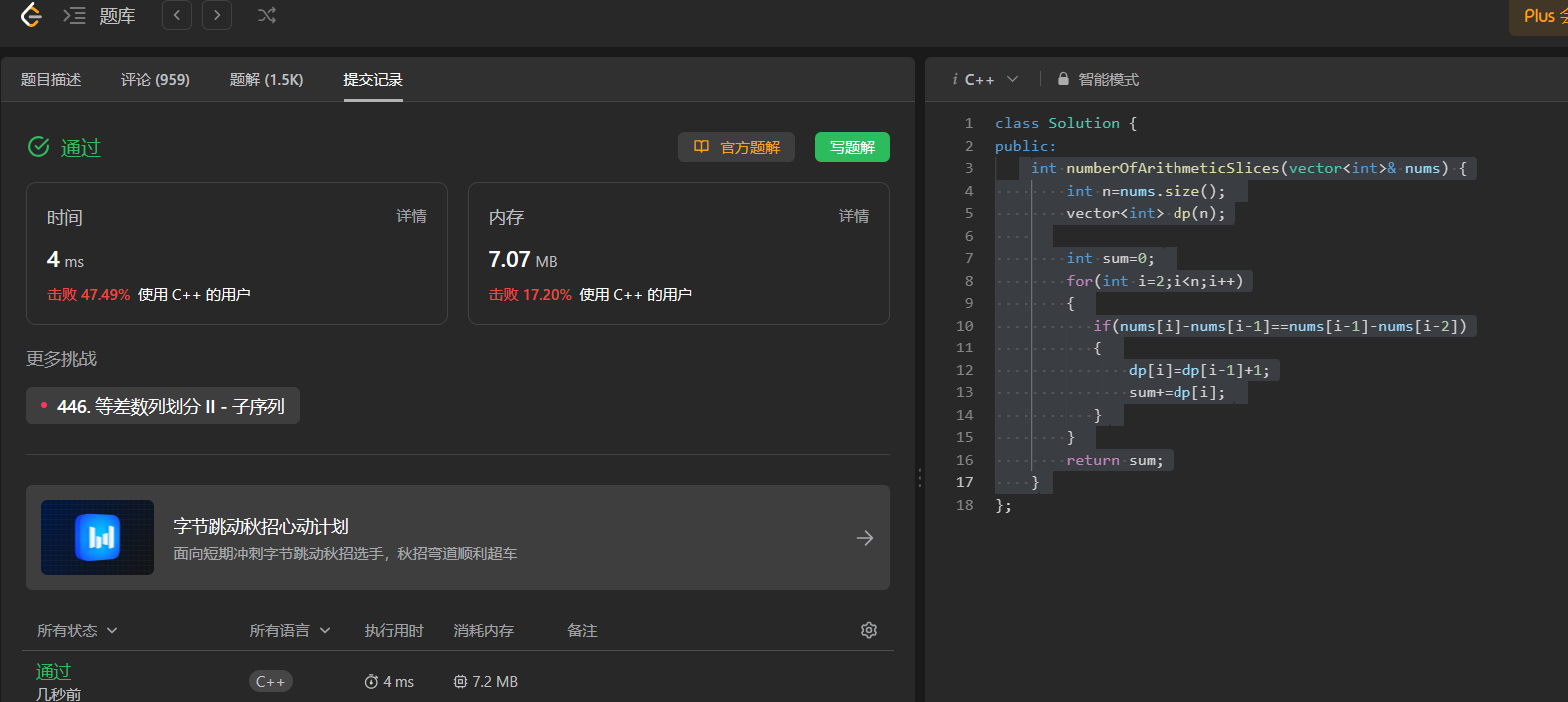
代码:
int numberOfArithmeticSlices(vector<int>& nums) {int n=nums.size();vector<int> dp(n);int sum=0;for(int i=2;i<n;i++){if(nums[i]-nums[i-1]==nums[i-1]-nums[i-2]){dp[i]=dp[i-1]+1;sum+=dp[i];}}return sum;}
978. 最长湍流子数组
链接: 978. 最长湍流子数组
给定一个整数数组 arr ,返回 arr 的 最大湍流子数组的长度 。
如果比较符号在子数组中的每个相邻元素对之间翻转,则该子数组是 湍流子数组 。
更正式地来说,当 arr 的子数组 A[i], A[i+1], …, A[j] 满足仅满足下列条件时,我们称其为湍流子数组:
若 i <= k < j :
当 k 为奇数时, A[k] > A[k+1],且
当 k 为偶数时,A[k] < A[k+1];
或 若 i <= k < j :
当 k 为偶数时,A[k] > A[k+1] ,且
当 k 为奇数时, A[k] < A[k+1]。
示例 1:
输入:arr = [9,4,2,10,7,8,8,1,9]
输出:5
解释:arr[1] > arr[2] < arr[3] > arr[4] < arr[5]
示例 2:
输入:arr = [4,8,12,16]
输出:2
示例 3:
输入:arr = [100]
输出:1
1.状态表示*
需要两个 dp 表:
- f[i] 表⽰:以 i 位置元素为结尾的所有⼦数组中,最后呈现「上升状态」下的最⻓湍流数组的⻓度;
- g[i] 表⽰:以 i 位置元素为结尾的所有⼦数组中,最后呈现「下降状态」下的最⻓湍流数组的⻓度
2.状态转移方程
对于 i 位置的元素 arr[i] ,有下⾯两种情况:
-
i. arr[i] > arr[i - 1] :如果 i 位置的元素⽐ i - 1 位置的元素⼤,说明接下来 应该去找 i -1 位置结尾,并且 i - 1 位置元素⽐前⼀个元素⼩的序列,那就是 g[i- 1] 。更新 f[i] 位置的值: f[i] = g[i - 1] + 1 ;
-
ii. arr[i] < arr[i - 1] :如果 i 位置的元素⽐ i - 1 位置的元素⼩,说明接下来 应该去找 i - 1位置结尾,并且 i - 1 位置元素⽐前⼀个元素⼤的序列,那就是 f[i - 1] 。更新 g[i] 位置的值: g[i] = f[i- 1] + 1 ;
-
ii. arr[i] == arr[i - 1] :不构成湍流数组。
3. 初始化
所有的元素「单独」都能构成⼀个湍流数组,因此可以将 dp 表内所有元素初始化为 1 。 由于⽤到前⾯的状态,因此我们循环的时候从第⼆个位置开始即可
4. 填表顺序
根「从左往右,两个表⼀起填」
5. 返回值
应该返回「两个 dp 表⾥⾯的最⼤值」
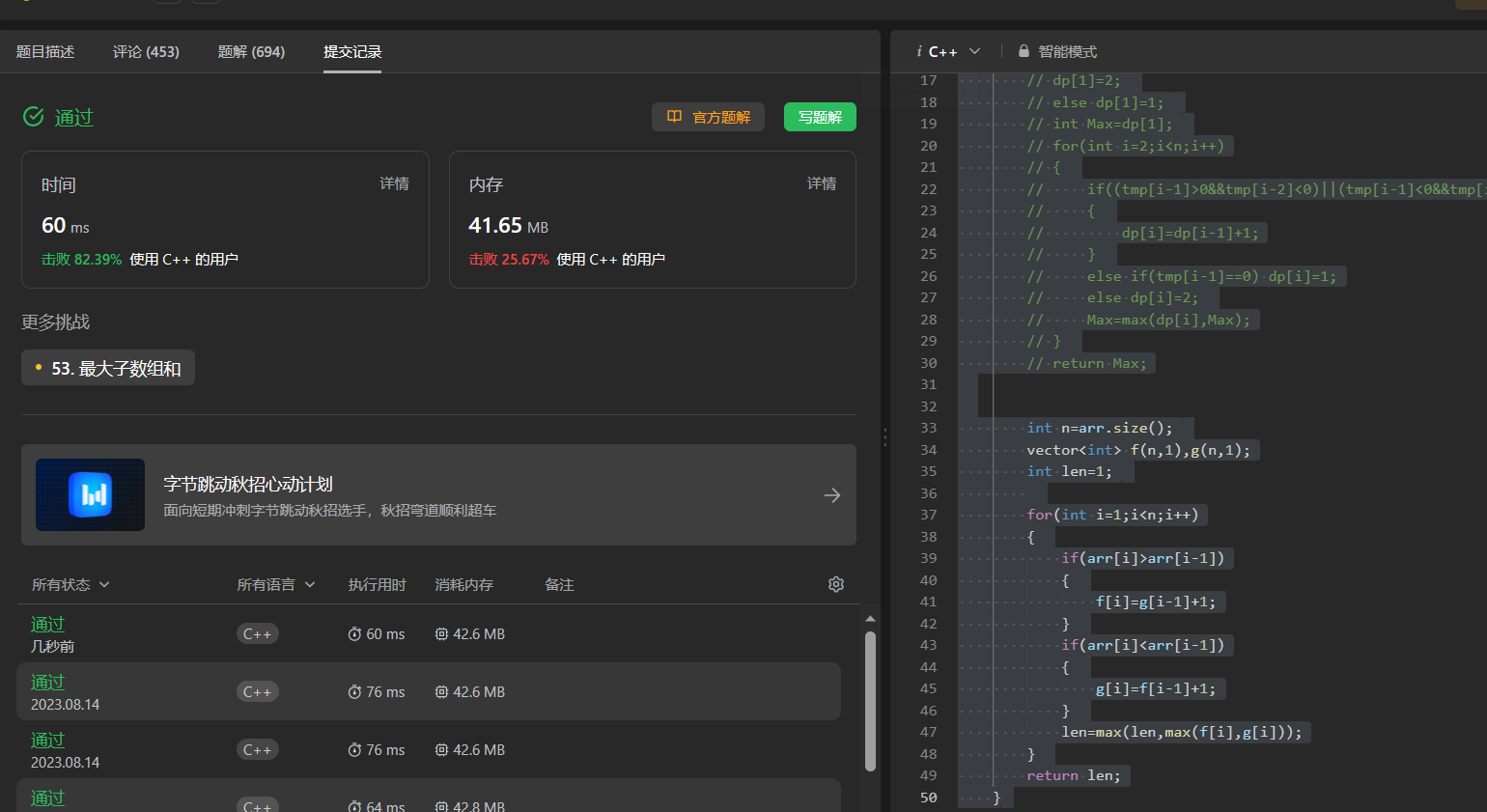
代码:
int maxTurbulenceSize(vector<int>& arr) {int n=arr.size();vector<int> f(n,1),g(n,1);int len=1;for(int i=1;i<n;i++){if(arr[i]>arr[i-1]){f[i]=g[i-1]+1;}if(arr[i]<arr[i-1]){g[i]=f[i-1]+1;}len=max(len,max(f[i],g[i]));}return len;}
相关文章:

【动态规划刷题 10】等差数列划分 最长湍流子数组
413. 等差数列划分 链接: 413. 等差数列划分 如果一个数列 至少有三个元素 ,并且任意两个相邻元素之差相同,则称该数列为等差数列。 例如,[1,3,5,7,9]、[7,7,7,7] 和 [3,-1,-5,-9] 都是等差数列。 给你一个整数数组 nums ,返回…...

redis 配置与优化
目录 一、关系数据库和非关系型数据库 二、关系型数据库和非关系型数据库区别 三、非关系型数据库产生背景 四、redis 1、概念 2、redis的优点 3、redis为什么这么快 五、redis安装与配置 一、关系数据库和非关系型数据库 关系型数据库:关系型数据库是一个结…...

数据结构例题代码及其讲解-递归与树
树 树的很多题目中都包含递归的思想 递归 递归包括递归边界以及递归式 即:往下递,往上归 递归写法的特点:写起来代码较短,但是时间复杂度较高 01 利用递归求解 n 的阶乘。 int Func(int n) {if (n 0) {return 1;}else …...

Jenkins | 流水线构建使用expect免密交互时卡住,直接退出
注意: expect 脚本必须以 interact 或 expect eof 结束。 原因: interact:使用interact会保持在终端而不会退回到原终端,所以就卡在这里。 expect eof:expect脚本默认的是等待10s,当执行完命令后,自动切回…...

git修改默认分支
git checkout 分支 切换到当前分支 git branch --set-upstream-toorigin/complete(远程分支名) 设置当前分支的上游分支为远程分支complete git branch --unset-upstream master 取消master上游分支的身份 现在,使用git commit,git push 命令可以直接…...
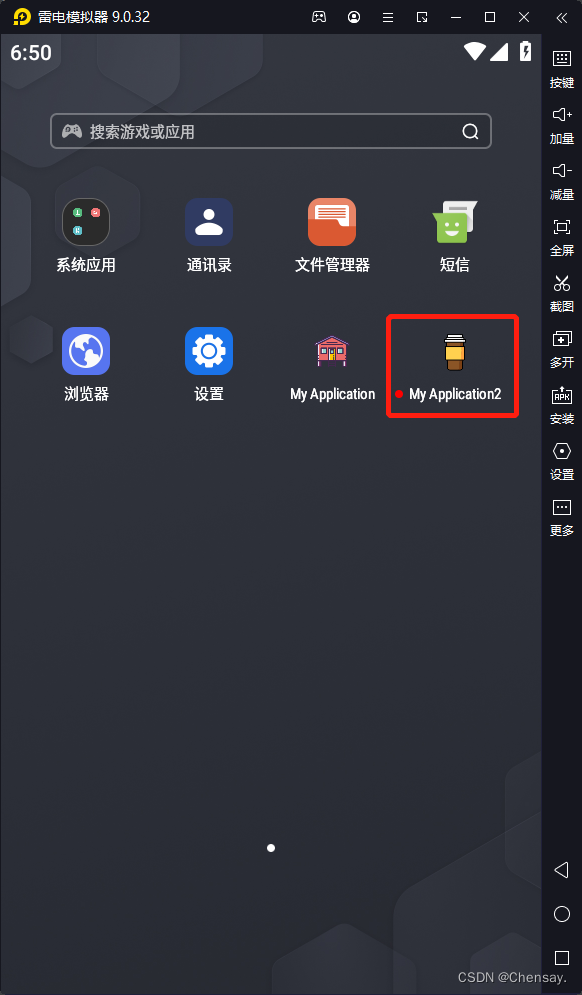
Android Studio开发入门教程:如何更改APP的图标?
更改APP的图标(安卓系统) 环境:Windows10、Android Studio版本如下图、雷电模拟器。 推荐图标库 默认APP图标 将新图标拉进src/main/res/mipmap-hdpi文件夹(一般app的icon图标是存放在mipmap打头的文件夹下的) 更改sr…...

MATLAB/Python的编程教程: 匹配滤波器的实现
MATLAB/Python的编程教程: 匹配滤波器的实现 注1:本文系“MATLAB/Python的编程教程”系列之一,致力于使用Python和Matlab实现特定的功能。本次要实现的功能是:匹配滤波器的实现。 匹配滤波器,这是一个在信号处理领域常见的主题,主要用于增强特定信号的检测性能,特别是在噪…...
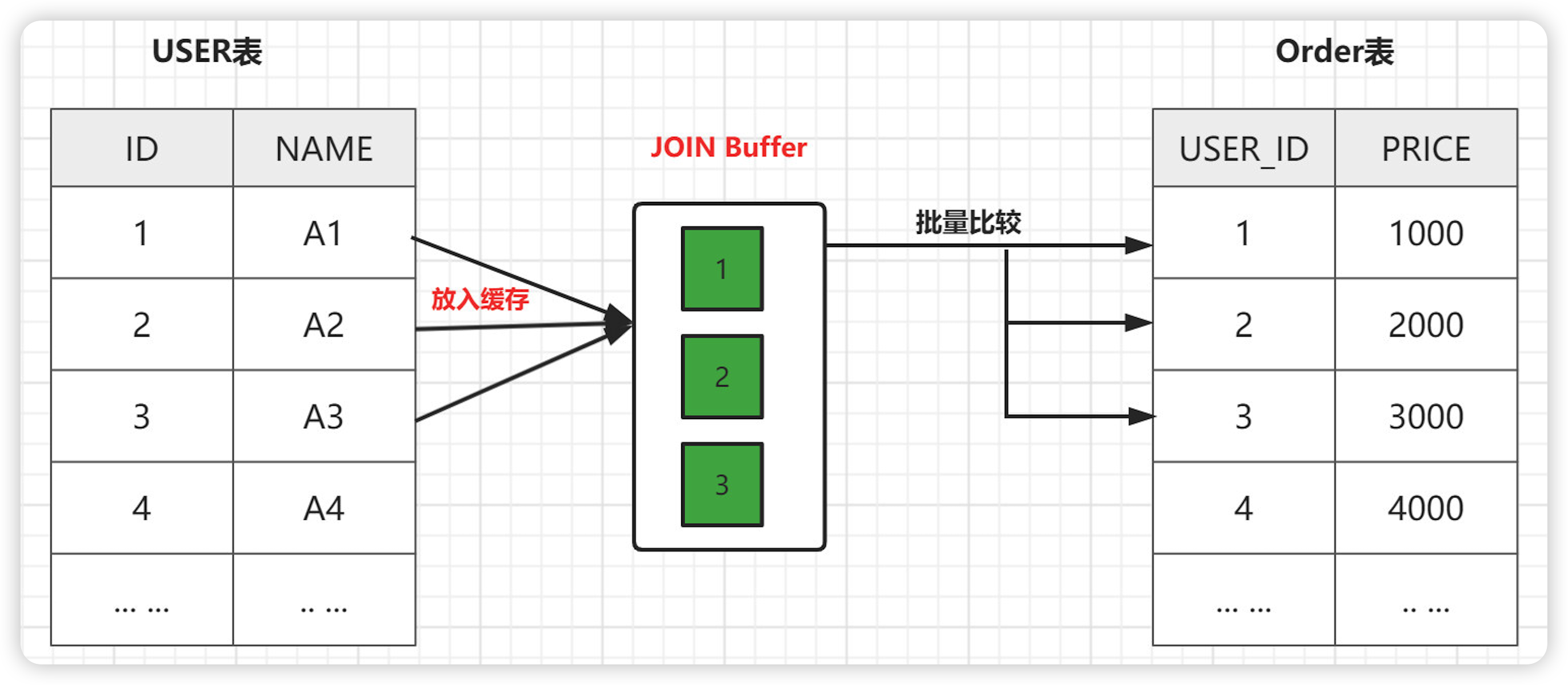
java八股文面试[数据库]——JOIN优化
JOIN 是 MySQL 用来进行联表操作的,用来匹配两个表的数据,筛选并合并出符合我们要求的结果集。 JOIN 操作有多种方式,取决于最终数据的合并效果。常用连接方式的有以下几种: 什么是驱动表 ? 多表关联查询时,第一个被处理的表就是驱动表,使用…...
Java语法中一些需要注意的点(仅用于个人学习)
1.当字符串和其他类型相加时,基本都是字符串,这与运算顺序有关。 2.Java中用ctrl d 来结束循环输入。 3.nextLine() 遇到空格不会结束。 4.方法重载 4.1. 方法名必须相同 4.2. 参数列表必须不同(参数的个数不同、参数的类型不同、类型的次序必须不…...

golang 线程 定时器 --chatGPT
问:线程函数write(ch,timer),功能为启动一个线程,循环执行打印,打印条件为触发ch chane 或 timer定时器每隔一段时间会触发 GPT:以下是一个示例Golang代码,其中有一个名为 write 的线程函数,它会在触发ch通道或每隔一…...

java 编程 7个简单的调优技巧
你的Java性能调优有救了!分享7个简单实用的Java性能调优技巧 一、以编程方式连接字符串 在Java中有很多不同的连接字符串的选项。比如,可以使用简单的或、良好的旧StringBuffer或StringBuilder。 那么,应该选择哪种方法? 答案取…...

03-Dockerfile
Dockerfile简介 Dockerfile是什么? Dockerfile是用来构建Docker镜像的文本文件,是由一条条构建镜像所需的指令和参数构成的脚本 Dockerfile官网 https://docs.docker.com/engine/reference/builder/ Dockerfile构建三步曲 编写Dockerfile文件docke…...

【AI】机器学习——朴素贝叶斯
文章目录 2.1 贝叶斯定理2.1.1 贝叶斯公式推导条件概率变式 贝叶斯公式 2.1.2 贝叶斯定理2.1.3 贝叶斯决策基本思想 2.2 朴素贝叶斯2.2.1 朴素贝叶斯分类器思想2.2.2 条件独立性对似然概率计算的影响2.2.3 基本方法2.2.4 模型后验概率最大化损失函数期望风险最小化策略 2.2.5 朴…...

数学建模:模糊综合评价分析
🔆 文章首发于我的个人博客:欢迎大佬们来逛逛 数学建模:模糊综合评价分析 文章目录 数学建模:模糊综合评价分析综合评价分析常用评价方法一级模糊综合评价综合代码 多级模糊综合评价总结 综合评价分析 构成综合评价类问题的五个…...

智能小车—PWM方式实现小车调速和转向
目录 1. 让小车动起来 2. 串口控制小车方向 3. 如何进行小车PWM调速 4. PWM方式实现小车转向 1. 让小车动起来 电机模块开发 L9110s概述 接通VCC,GND 模块电源指示灯亮, 以下资料来源官方,具体根据实际调试 IA1输入高电平,…...

Getx其他高级API
// 给出当前页面的args。 Get.arguments//给出以前的路由名称 Get.previousRoute// 给出要访问的原始路由,例如,rawRoute.isFirst() Get.rawRoute// 允许从GetObserver访问Rounting API。 Get.routing// 检查 snackbar 是否打开 Get.isSnackbarOpen// 检…...

npm/yarn link 测试包时报错 Warning: Invalid hook call. Hooks can only be called ...
使用 dumi 开发 React 组件库时,为避免每次修改都发布到 npm,需要在本地的测试项目中使用 npm link 为组件库建立软连接,方便本地调试。 结果在本地测试项目使用 $ npm link 组件库 后,使用内部组件确报错: react.dev…...
「网页开发|前端开发|Vue」06 公共组件与嵌套路由:让每一个页面都平等地拥有导航栏
本文主要介绍在多个页面存在相同部分时,如何提取公共组件然后在多个页面中导入组件重复使用来减少重复代码。在这基础上介绍了通过嵌套路由的方式来避免页面较多或公共部分较多的情况下,避免不断手动导入公共组件的麻烦,并且加快页面跳转的速…...

leetcode687. 最长同值路径(java)
最长同值路径 题目描述DFS 深度遍历代码演示 题目描述 难度 - 中等 LC - 687. 最长同值路径 给定一个二叉树的 root ,返回 最长的路径的长度 ,这个路径中的 每个节点具有相同值 。 这条路径可以经过也可以不经过根节点。 两个节点之间的路径长度 由它们之…...
MySQL的常用术语
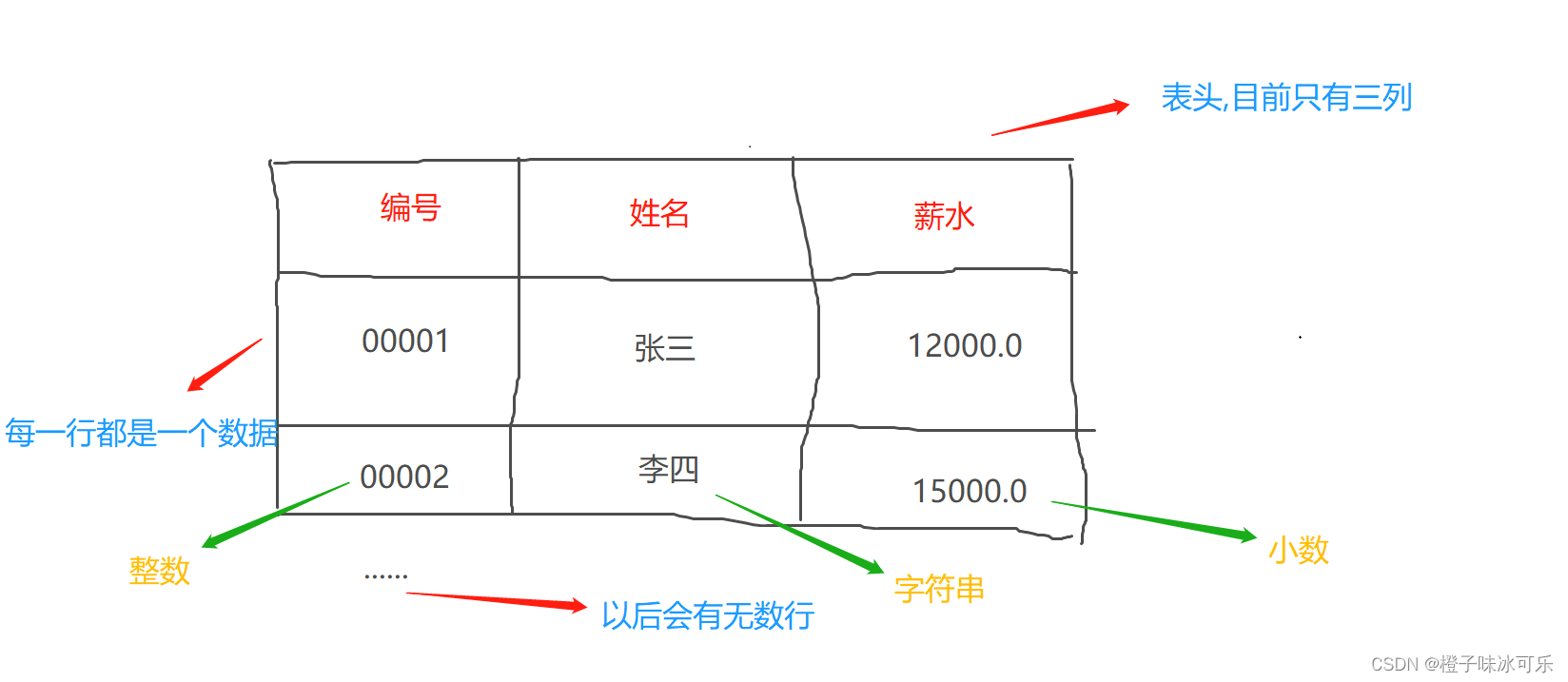
目录 1.关系 2.元组 3.属性 MySQL从小白到总裁完整教程目录:https://blog.csdn.net/weixin_67859959/article/details/129334507?spm1001.2014.3001.5502 1.关系 前面的博客有说到,MySQL是一款关系型数据库管理软件,一个关系就是 一张二维表(表) 我想大家都知道表格怎么…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...
-----深度优先搜索(DFS)实现)
c++ 面试题(1)-----深度优先搜索(DFS)实现
操作系统:ubuntu22.04 IDE:Visual Studio Code 编程语言:C11 题目描述 地上有一个 m 行 n 列的方格,从坐标 [0,0] 起始。一个机器人可以从某一格移动到上下左右四个格子,但不能进入行坐标和列坐标的数位之和大于 k 的格子。 例…...

【ROS】Nav2源码之nav2_behavior_tree-行为树节点列表
1、行为树节点分类 在 Nav2(Navigation2)的行为树框架中,行为树节点插件按照功能分为 Action(动作节点)、Condition(条件节点)、Control(控制节点) 和 Decorator(装饰节点) 四类。 1.1 动作节点 Action 执行具体的机器人操作或任务,直接与硬件、传感器或外部系统…...

三体问题详解
从物理学角度,三体问题之所以不稳定,是因为三个天体在万有引力作用下相互作用,形成一个非线性耦合系统。我们可以从牛顿经典力学出发,列出具体的运动方程,并说明为何这个系统本质上是混沌的,无法得到一般解…...

(转)什么是DockerCompose?它有什么作用?
一、什么是DockerCompose? DockerCompose可以基于Compose文件帮我们快速的部署分布式应用,而无需手动一个个创建和运行容器。 Compose文件是一个文本文件,通过指令定义集群中的每个容器如何运行。 DockerCompose就是把DockerFile转换成指令去运行。 …...

Python实现简单音频数据压缩与解压算法
Python实现简单音频数据压缩与解压算法 引言 在音频数据处理中,压缩算法是降低存储成本和传输效率的关键技术。Python作为一门灵活且功能强大的编程语言,提供了丰富的库和工具来实现音频数据的压缩与解压。本文将通过一个简单的音频数据压缩与解压算法…...

解析两阶段提交与三阶段提交的核心差异及MySQL实现方案
引言 在分布式系统的事务处理中,如何保障跨节点数据操作的一致性始终是核心挑战。经典的两阶段提交协议(2PC)通过准备阶段与提交阶段的协调机制,以同步决策模式确保事务原子性。其改进版本三阶段提交协议(3PC…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...

计算机系统结构复习-名词解释2
1.定向:在某条指令产生计算结果之前,其他指令并不真正立即需要该计算结果,如果能够将该计算结果从其产生的地方直接送到其他指令中需要它的地方,那么就可以避免停顿。 2.多级存储层次:由若干个采用不同实现技术的存储…...
