Python功能强大、灵活可扩展的Statsmodels库
Statsmodels是一个功能强大、灵活可扩展的Python库,用于进行统计建模和数据分析。它提供了一系列丰富的统计模型和方法,可以帮助研究人员和数据科学家在Python环境中进行高级统计分析。
概述
在Statsmodels中,线性回归是最常用的统计模型之一。线性回归可以用来建立因变量和一个或多个自变量之间的线性关系。Statsmodels提供了丰富的统计工具,用于评估模型的拟合优度、参数估计的显著性等。此外,Statsmodels还支持多种回归模型的扩展,如岭回归、Lasso回归等。这些模型可以帮助研究人员更好地理解数据之间的关系,并进行预测和决策。
广义线性模型是另一个强大的统计模型,可以处理因变量不满足正态分布假设的情况。Statsmodels提供了广义线性模型的实现,包括二项式回归、泊松回归、负二项式回归等。这些模型可以用于分析二元数据、计数数据等。广义线性模型的灵活性使得研究人员能够更好地适应不同类型的数据,并进行准确的分析和预测。
时间序列分析是一种用于处理时间相关数据的统计方法。Statsmodels提供了丰富的时间序列模型,包括ARIMA模型、VAR模型、GARCH模型等。这些模型可以用于预测未来的时间序列数据,分析时间序列之间的关系等。时间序列分析在金融、经济学等领域具有广泛的应用,Statsmodels提供了强大的工具和方法,帮助研究人员进行准确的时间序列分析。
Statsmodels还支持非参数方法,如核密度估计、非参数回归等。这些方法可以用于处理数据分布未知或不满足特定分布假设的情况。非参数方法的灵活性使得研究人员能够更好地适应不同类型的数据,并进行准确的分析和预测。
除了以上提到的统计模型,Statsmodels还提供了其他功能,如假设检验、方差分析、因子分析等。这些功能使得Statsmodels成为一个全面的统计分析工具。研究人员和数据科学家可以使用Statsmodels进行数据探索、模型建立和结果解释等工作。
总之,Statsmodels是一个功能强大、灵活可扩展的Python库,适用于各种统计建模和数据分析任务。无论是线性回归、广义线性模型、时间序列分析还是非参数方法,Statsmodels都提供了丰富的工具和方法。研究人员和数据科学家可以充分利用Statsmodels的功能,进行高级统计分析,从而更好地理解数据、做出准确的预测和决策。
案例
当使用Statsmodels进行统计建模和数据分析时,可以应用于各种实际案例。以下是一些示例:
1. 线性回归案例:
假设你是一家电子商务公司的数据科学家,你想了解广告投入和销售额之间的关系。你可以使用Statsmodels中的线性回归模型来建立广告投入和销售额之间的线性关系模型,并评估广告对销售额的影响。通过分析模型的拟合优度和参数估计的显著性,你可以得出结论并提出相应的决策建议。
import statsmodels.api as sm
import pandas as pd# 假设你有广告投入和销售额的数据
data = pd.read_csv('data.csv')# 添加常数列作为回归模型的截距
data['intercept'] = 1# 定义自变量和因变量
X = data[['intercept', '广告投入']]
y = data['销售额']# 拟合线性回归模型
model = sm.OLS(y, X)
results = model.fit()# 打印模型摘要
print(results.summary())
2. 广义线性模型案例:
假设你是一家医疗保险公司的数据分析师,你想了解吸烟与患病风险之间的关系。你可以使用Statsmodels中的二项式回归模型来建立吸烟与患病风险之间的关系模型,并评估吸烟对患病风险的影响。通过分析模型的拟合优度和参数估计的显著性,你可以得出结论并提供相关的医疗保险策略建议。
import statsmodels.api as sm
import pandas as pd# 假设你有吸烟和患病风险的数据
data = pd.read_csv('data.csv')# 添加常数列作为回归模型的截距
data['intercept'] = 1# 定义自变量和因变量
X = data[['intercept', '吸烟']]
y = data['患病风险']# 拟合二项式回归模型
model = sm.GLM(y, X, family=sm.families.Binomial())
results = model.fit()# 打印模型摘要
print(results.summary())
3. 时间序列分析案例:
假设你是一家零售公司的销售分析师,你想预测未来几个季度的销售额。你可以使用Statsmodels中的ARIMA模型来建立销售额的时间序列模型,并进行未来销售额的预测。通过分析模型的拟合优度和预测准确性,你可以制定相应的销售策略和库存管理计划。
import statsmodels.api as sm
import pandas as pd# 假设你有销售额的时间序列数据
data = pd.read_csv('data.csv')# 将时间列设置为索引
data['时间'] = pd.to_datetime(data['时间'])
data.set_index('时间', inplace=True)# 拟合ARIMA模型
model = sm.tsa.ARIMA(data, order=(1, 1, 1))
results = model.fit()# 进行未来销售额的预测
forecast = results.predict(start='2023-09-05', end='2023-12-31')# 打印预测结果
print(forecast)
4. 非参数方法案例:
假设你是一家市场调研公司的数据分析师,你想了解产品价格与销售量之间的关系,但你不知道价格和销售量的分布情况。你可以使用Statsmodels中的核密度估计方法来估计价格和销售量的分布,并通过非参数回归方法来建立价格与销售量之间的关系模型。通过分析估计的分布和模型的拟合优度,你可以得出结论并提供相关的市场调研建议。
import statsmodels.api as sm
import pandas as pd# 假设你有产品价格和销售量的数据
data = pd.read_csv('data.csv')# 估计价格和销售量的分布
price_density = sm.nonparametric.KDEUnivariate(data['价格'])
price_density.fit()sales_density = sm.nonparametric.KDEUnivariate(data['销售量'])
sales_density.fit()# 建立价格与销售量之间的关系模型
model = sm.nonparametric.KernelReg(data['销售量'], data['价格'], var_type='c')
results = model.fit()# 打印模型摘要
print(results.summary())
这些案例只是Statsmodels在统计建模和数据分析中的一小部分应用示例。Statsmodels提供了丰富的统计模型和方法,可以适用于各种实际问题的分析和预测。无论是在商业、医疗、金融还是其他领域,Statsmodels都可以帮助研究人员和数据科学家进行高级统计分析,从而更好地理解数据、做出准确的预测和决策。
练习题
当然,我可以给你一些统计学的练习题。请注意,以下是一些基础的练习题,如果你需要更具挑战性的题目,请告诉我。
-
一个班级有30个学生,他们的数学考试成绩如下:[85, 92, 78, 90, 88, 75, 80, 95, 85, 92, 78, 90, 88, 75, 80, 95, 85, 92, 78, 90, 88, 75, 80, 95, 85, 92, 78, 90, 88, 75]。计算这些学生的平均成绩、中位数和标准差。
-
一家公司的销售额数据如下:[1000, 2000, 1500, 3000, 2500]。计算这些销售额的总和、平均值和方差。
-
一个实验中,测量了一组学生的身高(单位:厘米),结果如下:[165, 170, 168, 172, 175, 180, 178, 182, 185, 190]。计算这组数据的范围、中程数和四分位数。
-
一家餐厅的顾客数量数据如下:[50, 60, 70, 80, 90, 100, 110, 120, 130, 140]。计算这些数据的偏度和峰度。
希望这些练习题能帮助你巩固统计学的基础知识。如果你有任何问题或需要更多练习题,请随时告诉我。
相关文章:

Python功能强大、灵活可扩展的Statsmodels库
Statsmodels是一个功能强大、灵活可扩展的Python库,用于进行统计建模和数据分析。它提供了一系列丰富的统计模型和方法,可以帮助研究人员和数据科学家在Python环境中进行高级统计分析。 概述 在Statsmodels中,线性回归是最常用的统计模型之…...

AcWing 4405. 统计子矩阵(每日一题)
如果你觉得这篇题解对你有用,可以点点关注再走呗~ 题目描述 给定一个 NM 的矩阵 A,请你统计有多少个子矩阵 (最小 11,最大 NM) 满足子矩阵中所有数的和不超过给定的整数 K ? 输入格式 第一行包含三个整数 N,M 和 K。 之后 N 行每行包含 …...

Kali Linux渗透测试技术介绍【文末送书】
文章目录 写在前面一、什么是Kali Linux二、渗透测试基础概述和方法论三、好书推荐1. 书籍简介2. 读者对象3. 随书资源 写作末尾 写在前面 对于企业网络安全建设工作的质量保障,业界普遍遵循PDCA(计划(Plan)、实施(Do…...
GPT与BERT模型
NLP任务的核心逻辑是“猜概率”的游戏。BERT和GPT都是基于预训练语言模型的思想,通过大量语料训练得到语言模型。两种模型都是基于Transformer模型。 Bert 类似于Transformer的Encoder部分,GPT类似于Transformer的Decoder部分。两者最明显的在结构上的差…...

2023-09-06力扣每日一题-摆烂暴力
链接: [1123. 最深叶节点的最近公共祖先](https://leetcode.cn/problems/form-smallest-number-from-two-digit-arrays/) 题意: 如题 解: 今天搞一手暴力,按层存,按层取,直到只取到一个 实际代码&…...

【Flutter】Flutter 使用 timego 将日期转换为时间描述
【Flutter】Flutter 使用 timego 将日期转换为时间描述 文章目录 一、前言二、安装与基本使用三、如何添加新的语言四、如何覆盖现有的语言或添加自定义消息五、完整示例六、总结 一、前言 你好!我是小雨青年,今天我要为你介绍一个非常实用的 Flutter 包…...
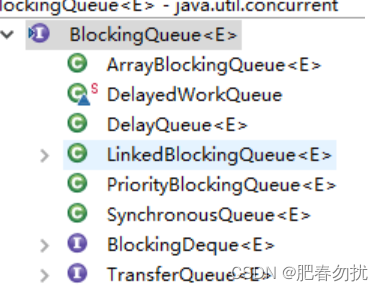
并发容器11
一 JDK 提供的并发容器总结 JDK 提供的这些容器大部分在 java.util.concurrent 包中。 ConcurrentHashMap: 线程安全的 HashMap CopyOnWriteArrayList: 线程安全的 List,在读多写少的场合性能非常好,远远好于 Vector. ConcurrentLinkedQueue: 高效的并…...
Java8实战-总结22
Java8实战-总结22 使用流数值流原始类型流特化数值范围数值流应用:勾股数 使用流 数值流 可以使用reduce方法计算流中元素的总和。例如,可以像下面这样计算菜单的热量: int calories menu.stream().map(Dish::getcalories).reduce(0, Int…...

matlab 实现点云ICP 配准算法
一、算法步骤 (1)在目标点云P中取点集pi∈P; (2)找出源点云Q中的对应点集qi∈Q,使得||qi-pi||=min; (3)计算旋转矩阵R和平移矩阵t,使得误差函数最小; (4)对pi使用上一步求得的旋转矩阵R和平移矩阵t进行旋转和平移变换,的到新的对应点集pi’={pi’=Rpi+t,pi∈P};…...

python提取word文本和word图片
提取文本 docx只支持docx格式,所以如果想读取doc需要另存为docx格式即可 import docx # pip3 install python-docx doc docx.Document(three.docx) for paragraph in doc.paragraphs:print(paragraph.text)提取图片 import zipfile import os, re # docx本质上…...

iOS开发Swift-9-SFSymbols,页面跳转,view屏幕比例,启动页-和风天气AppUI
1.创建项目 2.设置好测试机型,App显示名称,以及关闭横向展示. 3.下载SF Symbols. https://developer.apple.com/sf-symbols/ 右上角搜索 search ,可以找到很多系统自带图标.选择喜欢的图标,拷贝图标的名字. 插入一个Button,在Image中粘贴图标名称并选择,即可将Button变成想要的…...
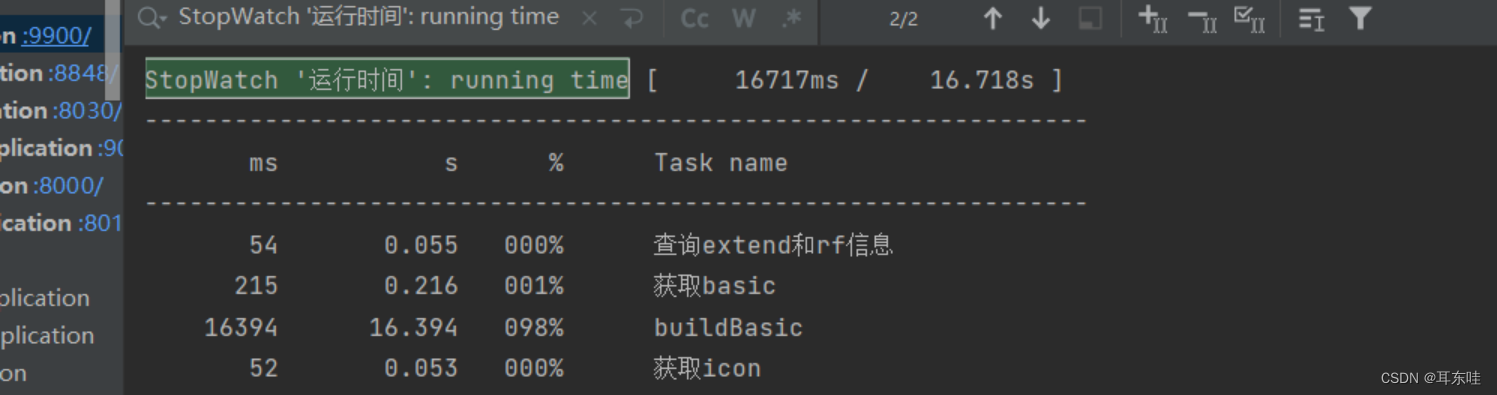
代码优化工具-测试程序执行时间-IDEAdebug+StopWatch
参考: [技巧]IDEA的debugStopWatch监测程序运行时间 添加链接描述 1创建类StopWatchExpand import lombok.extern.slf4j.Slf4j;import org.springframework.util.StopWatch;import java.text.NumberFormat;/*** 检测程序片段运行时间拓展** author sdevil507* cr…...
力扣每日一题---2594. 修车的最少时间
文章目录 思路解题方法复杂度Code 思路 请注意,能力值越低,修车越快,应该翻译成「排名」,排名越靠前,修车越快。)根据题意可以知道r * n * n < t 的,所以可以利用数学知识进行改变公式&#…...
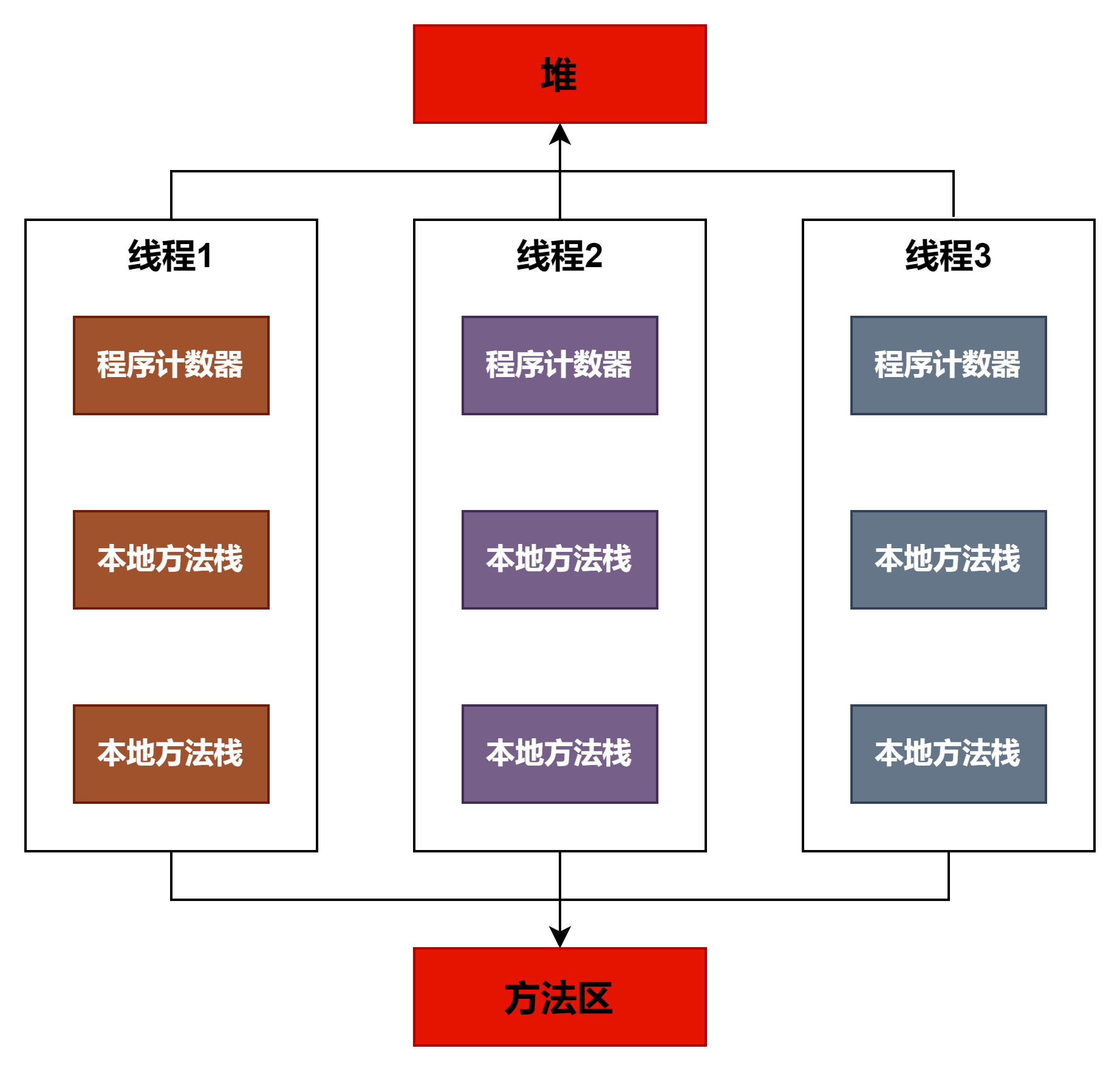
【jvm】运行时数据区
目录 一、运行时数据区一、作用二、说明三、线程共用与私有区域 一、运行时数据区 一、作用 1.内存是非常重要的系统资源,是硬盘和CPU 的中间仓库及桥梁,承载着操作系统和应用程序的实时运行。JVM内存布局规定了Java在运行过程中内存申请、分配、管理的策…...

SpringMVC相对路径和绝对路径
1.相对地址与绝对地址定义 在jsp,html中使用的地址,都是在前端页面中的地址,都是相对地址 地址分类:(1),绝对地址,带有协议名称的是绝对地址,http://www.baidu.com&…...
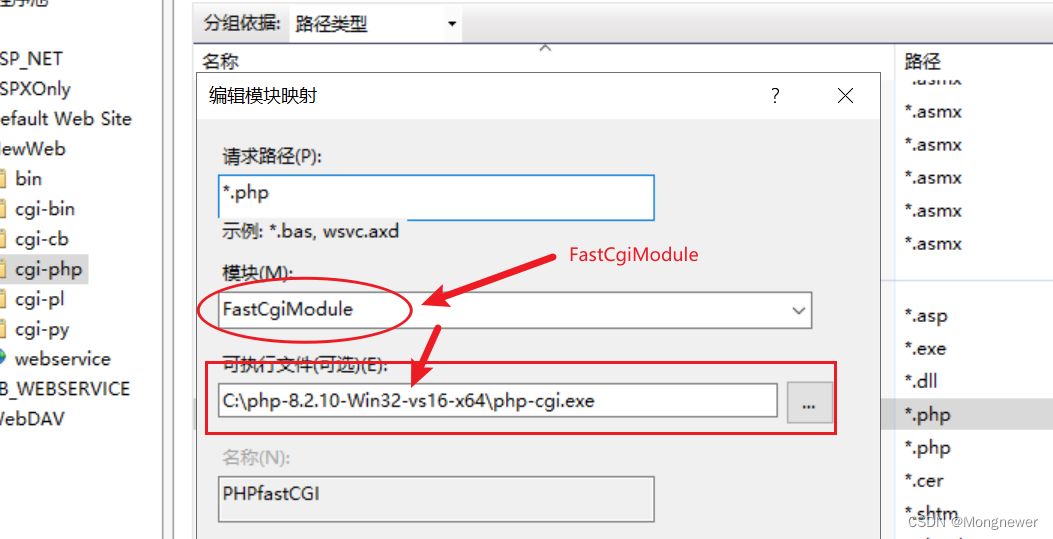
IIS perl python cbrother php脚本语言配置及简单测试样例程序
上篇笔记写了 IIS 配置 CGI, IIS CGI配置和CGI程序FreeBasic, VB6, VC 简单样例_Mongnewer的博客-CSDN博客 这篇在IIS上配置一些脚本语言。为了操作方便,每种语言在站点下分设文件夹。 1. IIS perl配置 Perl CGI方式是曾经流行的做法。先下载一个开源…...

Oracle Scheduler中日期表达式和PLSQL表达式的区别
参考文档: Database Administrator’s Guide 29.4.5.4 Differences Between PL/SQL Expression and Calendaring Syntax Behavior There are important differences in behavior between a calendaring expression and PL/SQL repeat interval. These differenc…...

Java设计模式:一、六大设计原则-06:依赖倒置原则
文章目录 一、定义:依赖倒置原则二、模拟场景:依赖倒置原则三、违背方案:依赖倒置原则3.1 工程结构3.2 抽奖系统**3.2.1 定义抽奖用户类**3.2.2 抽奖控制 3.3 单元测试 四、改善代码:依赖倒置原则4.1 工程结构4.2 抽奖控制改善4.2…...

信息系统数据同步解决方案
实施数据同步解决方案时,重要的是确保数据同步是安全的、可靠的,并且能够适应系统变化。定期测试和监控数据同步过程,以确保其稳定运行,并随着需求的变化进行适当的调整和优化。 应用场景:信息系统A和信息系统B实现员…...
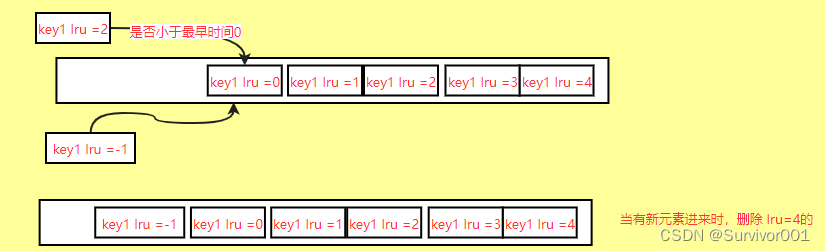
LRU算法 vs Redis近似LRU算法
LRU(Least Recently Use)算法,是用来判断一批数据中,最近最少使用算法。它底层数据结构由Hash和链表结合实现,使用Hash是为了保障查询效率为O(1),使用链表保障删除元素效率为O(1)。 LRU算法是用来判断最近最少使用到元素…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

AtCoder 第409场初级竞赛 A~E题解
A Conflict 【题目链接】 原题链接:A - Conflict 【考点】 枚举 【题目大意】 找到是否有两人都想要的物品。 【解析】 遍历两端字符串,只有在同时为 o 时输出 Yes 并结束程序,否则输出 No。 【难度】 GESP三级 【代码参考】 #i…...

Frozen-Flask :将 Flask 应用“冻结”为静态文件
Frozen-Flask 是一个用于将 Flask 应用“冻结”为静态文件的 Python 扩展。它的核心用途是:将一个 Flask Web 应用生成成纯静态 HTML 文件,从而可以部署到静态网站托管服务上,如 GitHub Pages、Netlify 或任何支持静态文件的网站服务器。 &am…...

ESP32 I2S音频总线学习笔记(四): INMP441采集音频并实时播放
简介 前面两期文章我们介绍了I2S的读取和写入,一个是通过INMP441麦克风模块采集音频,一个是通过PCM5102A模块播放音频,那如果我们将两者结合起来,将麦克风采集到的音频通过PCM5102A播放,是不是就可以做一个扩音器了呢…...

【Java_EE】Spring MVC
目录 Spring Web MVC 编辑注解 RestController RequestMapping RequestParam RequestParam RequestBody PathVariable RequestPart 参数传递 注意事项 编辑参数重命名 RequestParam 编辑编辑传递集合 RequestParam 传递JSON数据 编辑RequestBody …...

mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包
文章目录 现象:mysql已经安装,但是通过rpm -q 没有找mysql相关的已安装包遇到 rpm 命令找不到已经安装的 MySQL 包时,可能是因为以下几个原因:1.MySQL 不是通过 RPM 包安装的2.RPM 数据库损坏3.使用了不同的包名或路径4.使用其他包…...

鸿蒙DevEco Studio HarmonyOS 5跑酷小游戏实现指南
1. 项目概述 本跑酷小游戏基于鸿蒙HarmonyOS 5开发,使用DevEco Studio作为开发工具,采用Java语言实现,包含角色控制、障碍物生成和分数计算系统。 2. 项目结构 /src/main/java/com/example/runner/├── MainAbilitySlice.java // 主界…...
