【C++ 学习 ⑳】- 详解二叉搜索树
目录
一、概念
二、实现
2.1 - BST.h
2.2 - test.cpp
三、应用
四、性能分析
一、概念
二叉搜索树(BST,Binary Search Tree),又称二叉排序树或二叉查找树。
二叉搜索树是一棵二叉树,可以为空;如果不为空,满足以下性质:
-
非空左子树的所有键值小于其根节点的键值
-
非空右子树的所有键值大于其根节点的键值
-
左、右子树本身也都是二叉搜索树。

二、实现
2.1 - BST.h
#pragma once
#include <stack>
#include <iostream>
template<class K>
struct BSTNode
{BSTNode<K>* _left;BSTNode<K>* _right;K _key;
BSTNode(const K& key = K()): _left(nullptr), _right(nullptr), _key(key){ }
};
template<class K>
class BST
{typedef BSTNode<K> BSTNode;
public:/*---------- 构造函数和析构函数 ----------*/// 默认构造函数BST() : _root(nullptr){ }
// 拷贝构造函数(实现深拷贝)BST(const BST<K>& t){_root = Copy(t._root);}
// 析构函数~BST(){Destroy(_root);}
/*---------- 赋值运算符重载 ----------*/// 利用上面写好的拷贝构造函数实现深拷贝BST<K>& operator=(BST<K> tmp){std::swap(_root, tmp._root);return *this;}
/*---------- 插入 ----------*/// 非递归写法bool Insert(const K& key){if (_root == nullptr){_root = new BSTNode(key);return true;}
BSTNode* parent = nullptr;BSTNode* cur = _root;while (cur){parent = cur;if (key < cur->_key)cur = cur->_left;else if (key > cur->_key)cur = cur->_right;elsereturn false;}
cur = new BSTNode(key);if (key < parent->_key)parent->_left = cur;elseparent->_right = cur;return true;}
// 递归(Recursion)写法bool InsertRecursion(const K& key){return _InsertRecursion(_root, key);}
/*---------- 删除 ----------*/// 非递归写法bool Erase(const K& key){BSTNode* parent = nullptr;BSTNode* cur = _root;while (cur){if (key < cur->_key){parent = cur;cur = cur->_left;}else if (key > cur->_key){parent = cur;cur = cur->_right;}else{if (cur->_left == nullptr) // 左子树为空{if (parent == nullptr) // 或者 cur == _root{_root = cur->_right;}else{if (parent->_left == cur)parent->_left = cur->_right;elseparent->_right = cur->_right;}}else if (cur->_right == nullptr) // 右子树为空{if (parent == nullptr) // 或者 cur == _root{_root = cur->_left;}else{if (parent->_left == cur)parent->_left = cur->_left;elseparent->_right = cur->_left;}}else // 左、右子树非空{// 找到左子树中关键字最大的节点(或者找到右子树中关键字最小的节点)BSTNode* parentLeftMax = cur;BSTNode* leftMax = cur->_left;while (leftMax->_right){parentLeftMax = leftMax;leftMax = leftMax->_right;}// 让 leftMax 指向的节点代替 cur 指向的节点,然后删除 leftMax 指向的节点,// 这样就转换成了上面的情况std::swap(cur->_key, leftMax->_key);if (parentLeftMax->_left == leftMax) // 或者 parentLeftMax == curparentLeftMax->_left = leftMax->_left;elseparentLeftMax->_right = leftMax->_left;cur = leftMax;}delete cur;return true;}}return false;}
// 递归写法bool EraseRecursion(const K& key){return _EraseRecursion(_root, key);}
/*---------- 查找 ----------*/// 非递归写法bool Search(const K& key) const{BSTNode* cur = _root;while (cur){if (key < cur->_key)cur = cur->_left;else if (key > cur->_key)cur = cur->_right;elsereturn true;}return false;}
// 递归写法bool SearchRecursion(const K& key) const{return _SearchRecursion(_root, key);}
/*---------- 中序遍历 ----------*/// 非递归写法void InOrder() const{std::stack<BSTNode*> st;BSTNode* cur = _root;while (cur || !st.empty()){while (cur){st.push(cur);cur = cur->_left;}BSTNode* top = st.top();st.pop();std::cout << top->_key << " ";cur = top->_right;}std::cout << std::endl;}
// 递归写法void InOrderRecursion() const{_InOrderRecursion(_root);std::cout << std::endl;}
private:BSTNode* Copy(BSTNode* root){if (root == nullptr)return nullptr;
BSTNode* copyRoot = new BSTNode(root->_key);copyRoot->_left = Copy(root->_left);copyRoot->_right = Copy(root->_right);return copyRoot;}
void Destroy(BSTNode*& root){// 【注意:root 为 _root 或者某个节点的左或右指针的引用】if (root == nullptr)return;
Destroy(root->_left);Destroy(root->_right);delete root;root = nullptr;}
bool _InsertRecursion(BSTNode*& root, const K& key){// 【注意:root 为 _root 或者某个节点的左或右指针的引用】if (root == nullptr){root = new BSTNode(key);return true;}
if (key < root->_key)_InsertRecursion(root->_left, key);else if (key > root->_key)_InsertRecursion(root->_right, key);elsereturn false;}
bool _EraseRecursion(BSTNode*& root, const K& key){// 【注意:root 为 _root 或者某个节点的左或右指针的引用】if (root == nullptr)return false;
if (key < root->_key)_EraseRecursion(root->_left, key);else if (key > root->_key)_EraseRecursion(root->_right, key);else{BSTNode* tmp = root;if (root->_left == nullptr)root = root->_right;else if (root->_right == nullptr)root = root->_left;else{BSTNode* leftMax = root->_left;while (leftMax->_right){leftMax = leftMax->_right;}std::swap(leftMax->_key, root->_key);return _EraseRecursion(root->_left, key);}delete tmp;return true;}}
bool _SearchRecursion(BSTNode* root, const K& key) const{if (root == nullptr)return false;
if (key < root->_key)_SearchRecursion(root->_left, key);else if (key > root->_key)_SearchRecursion(root->_right, key);elsereturn true;}
void _InOrderRecursion(BSTNode* root) const{if (root == nullptr)return;
_InOrderRecursion(root->_left);std::cout << root->_key << " ";_InOrderRecursion(root->_right);}
private:BSTNode* _root;
};2.2 - test.cpp
#include "BST.h"
using namespace std;
void TestBST1()
{int arr[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };BST<int> t1;for (auto e : arr){t1.Insert(e);}t1.InOrder(); // 1 3 4 6 7 8 10 13 14
BST<int> t2(t1);t2.InOrder(); // 1 3 4 6 7 8 10 13 14
BST<int> t3;t3 = t1;t1.InOrder(); // 1 3 4 6 7 8 10 13 14
// 左子树为空t1.Erase(4);t1.InOrder(); // 1 3 6 7 8 10 13 14t1.Erase(6);t1.InOrder(); // 1 3 7 8 10 13 14// 右子树为空t1.Erase(14);t1.InOrder(); // 1 3 7 8 10 13// 左、右子树非空t1.Erase(8);t1.InOrder(); // 1 3 7 10 13
cout << t1.Search(8) << endl; // 0cout << t1.Search(7) << endl; // 1
}
void TestBST2()
{int arr[] = { 8, 3, 1, 10, 6, 4, 7, 14, 13 };BST<int> t;for (auto e : arr){t.InsertRecursion(e);}t.InOrderRecursion(); // 1 3 4 6 7 8 10 13 14
// 左子树为空t.EraseRecursion(4);t.InOrderRecursion(); // 1 3 6 7 8 10 13 14t.EraseRecursion(6);t.InOrderRecursion(); // 1 3 7 8 10 13 14// 右子树为空t.EraseRecursion(14);t.InOrderRecursion(); // 1 3 7 8 10 13// 左、右子树非空t.EraseRecursion(8);t.InOrderRecursion(); // 1 3 7 10 13
cout << t.SearchRecursion(8) << endl; // 0cout << t.SearchRecursion(7) << endl; // 1
}
int main()
{TestBST1();TestBST2();return 0;
}
三、应用
-
K 模型:结构体中只需要存储关键码 key,关键码即为需要搜索到的值。
例如,要判断一个单词是否拼写正确,我们首先把词库中的每个单词作为 key,构建一棵二叉搜索树,然后在这棵二叉搜索树中检索单词是否存在,若存在则表明拼写正确,不存在则表明拼写错误。
-
KV 模型:每个关键码 key,都有与之对应的值 value,即 <key, value> 的键值对。
这种模型在现实生活中也很常见:
-
比如英汉词典就是英文与中文的对应关系,通过英文可以快速找到与其对应的中文,英文单词与其对应的中文 <word, Chinese> 就构成一种键值对。
-
再比如统计单词次数,统计成功后,给定单词就可以快速找到其出现的次数,单词与其出现的次数 <word, count> 就构成一种键值对。
BST.h:#pragma once #include <iostream> template<class K, class V> struct BSTNode {BSTNode<K, V>* _left;BSTNode<K, V>* _right;K _key;V _value; BSTNode(const K& key = K(), const V& value = V()): _left(nullptr), _right(nullptr), _key(key), _value(value){ } }; template<class K, class V> class BST {typedef BSTNode<K, V> BSTNode; public:BST() : _root(nullptr){ } BST(const BST<K, V>& t){_root = Copy(t._root);} ~BST(){Destroy(_root);} BST<K, V>& operator=(BST<K, V> tmp){std::swap(_root, tmp._root);return *this;} bool Insert(const K& key, const V& value){return _Insert(_root, key, value);} bool Erase(const K& key){return _Erase(_root, key);} BSTNode* Search(const K& key) const{return _Search(_root, key);} void InOrder() const{_InOrder(_root);std::cout << std::endl;} private:BSTNode* Copy(BSTNode* root){if (root == nullptr)return nullptr; BSTNode* copyRoot = new BSTNode(root->_key, root->_value);copyRoot->_left = Copy(root->_left);copyRoot->_right = Copy(root->_right);return copyRoot;} void Destroy(BSTNode*& root){// 【注意:root 为 _root 或者某个节点的左或右指针的引用】if (root == nullptr)return; Destroy(root->_left);Destroy(root->_right);delete root;root = nullptr;} bool _Insert(BSTNode*& root, const K& key, const V& value){// 【注意:root 为 _root 或者某个节点的左或右指针的引用】if (root == nullptr){root = new BSTNode(key, value);return true;} if (key < root->_key)_Insert(root->_left, key, value);else if (key > root->_key)_Insert(root->_right, key, value);elsereturn false;} bool _Erase(BSTNode*& root, const K& key){// 【注意:root 为 _root 或者某个节点的左或右指针的引用】if (root == nullptr)return false; if (key < root->_key)_Erase(root->_left, key);else if (key > root->_key)_Erase(root->_right, key);else{BSTNode* tmp = root;if (root->_left == nullptr)root = root->_right;else if (root->_right == nullptr)root = root->_left;else{BSTNode* leftMax = root->_left;while (leftMax->_right){leftMax = leftMax->_right;}std::swap(leftMax->_key, root->_key);return _Erase(root->_left, key);}delete tmp;return true;}} BSTNode* _Search(BSTNode* root, const K& key) const{if (root == nullptr)return nullptr; if (key < root->_key)_Search(root->_left, key);else if (key > root->_key)_Search(root->_right, key);elsereturn root;} void _InOrder(BSTNode* root) const{if (root == nullptr)return; _InOrder(root->_left);std::cout << root->_key << " : " << root->_value << std::endl;_InOrder(root->_right);} private:BSTNode* _root; };test.cpp:#include "BST_KV.h" using namespace std; void TestBST1() {BST<string, string> t;t.Insert("insert", "插入");t.Insert("erase", "删除");t.Insert("search", "查找");t.Insert("left", "左边");t.Insert("right", "右边");// 输入英文单词,找到对应的中文string str;while (cin >> str){BSTNode<string, string>* ret = t.Search(str);if (ret)cout << str << "对应的中文是:" << ret->_value << endl;elsecout << "单词拼写错误,词库中没有此单词!" << endl;} } void TestBST2() {string arr[] = { "苹果", "西瓜", "苹果", "西瓜", "苹果", "苹果", "西瓜", "苹果", "香蕉", "苹果", "香蕉" };BST<string, int> t;// 统计每种水果出现的次数for (const auto& str : arr){BSTNode<string, int>* ret = t.Search(str);if (ret == nullptr)t.Insert(str, 1);elseret->_value += 1;}t.InOrder();// 苹果 : 6// 西瓜: 3// 香蕉 : 2 } int main() {// TestBST1();TestBST2();return 0; } -
四、性能分析
在二叉搜索树的插入和删除操作中,都必须先进行查找操作,所以查找的效率就代表了各个操作的性能。
对含 n 个节点的二叉搜索树,若每个节点查找的概率相等,则二叉搜树的平均查找长度是节点在二叉搜树树的深度的函数,即节点越深,比较次数越多。
但对于同一个关键码集合,如果各关键码插入的次序不同,可能得到不同结构的二叉搜索树,例如:
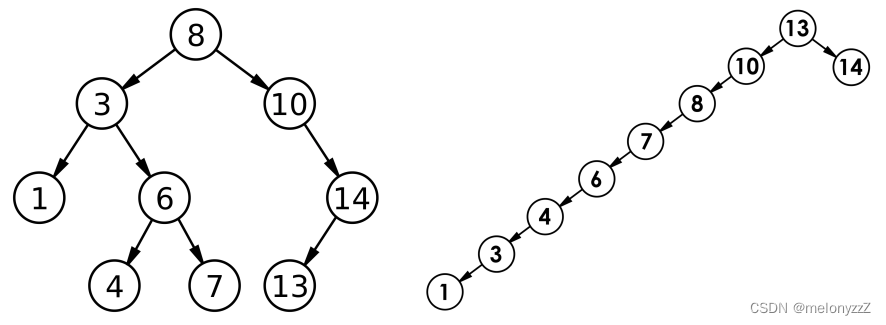
最好情况下,二叉搜索树为完全二叉树(或者接近完全二叉树),其平均比较次数为 。
最坏情况下,二叉搜索树退化为单支树(或者类似单支树),其平均比较次数为 。
如果退化成单支树,二叉搜树的性能就丢失了,那么能否改进,不论按照什么次序插入关键码,二叉搜索树的性能都能达到最优?
后续所要学习的 AVL 树和红黑树就可以解决上述问题。
相关文章:

【C++ 学习 ⑳】- 详解二叉搜索树
目录 一、概念 二、实现 2.1 - BST.h 2.2 - test.cpp 三、应用 四、性能分析 一、概念 二叉搜索树(BST,Binary Search Tree),又称二叉排序树或二叉查找树。 二叉搜索树是一棵二叉树,可以为空;如果不…...
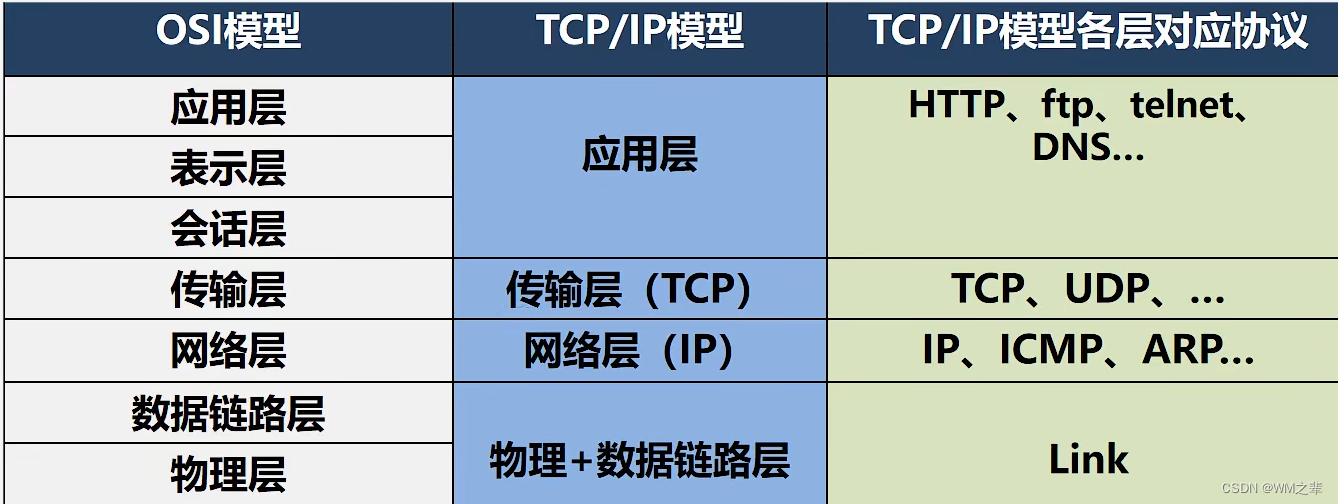
Java中网络的基本介绍。网络通信,网络,ip地址,域名,端口,网络通信协议,TCP/IP传输过程,网络通信协议模型,TCP协议,UDP协议
- 网络通信 概念:网络通信是指通过计算机网络进行信息传输的过程,包括数据传输、语音通话、视频会议等。在网络通信中,数据被分成一系列的数据包,并通过网络传输到目的地。在数据传输过程中,需要确保数据的完整性、准…...

【Qt】总体把握文本编码问题
在项目开发中,经常会遇到文本编码问题。文本编码知识非常基础,但对于新手来说,可能需要花费较长的时间去尝试,才能在脑海中建立对编码的正确认知。文本编码原理并不难,难的是在项目实践中掌握正确处理文本编码的方法。…...
之curl)
Linux命令(77)之curl
linux命令之curl 1.curl介绍 linux命令之curl是一款强大的http命令行工具,它支持文件的上传和下载,是综合传输工具。 2.curl用法 curl [参数] [url] curl参数 参数说明-C断点续传-o <filename>把输出写到filename文件中-x在给定的端口上使用HT…...

详解 sudo usermod -aG docker majn
这个命令涉及到几个 Linux 系统管理的基础概念,包括 sudo、usermod 和用户组管理。我们可以逐一地解析它们: sudo: sudo(superuser do)允许一个已经被授权的用户以超级用户或其他用户的身份执行一个命令。当使用 sudo 前缀一个命令…...
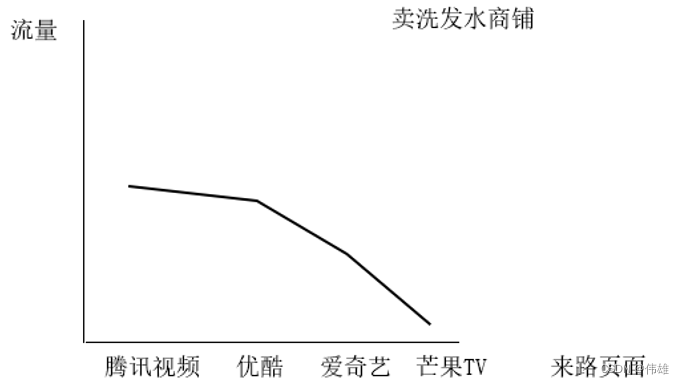
大数据课程L2——网站流量项目的算法分析数据处理
文章作者邮箱:yugongshiye@sina.cn 地址:广东惠州 ▲ 本章节目的 ⚪ 了解网站流量项目的算法分析; ⚪ 了解网站流量项目的数据处理; 一、项目的算法分析 1. 概述 网站流量统计是改进网站服务的重要手段之一,通过获取用户在网站的行为,可以分析出哪些内…...
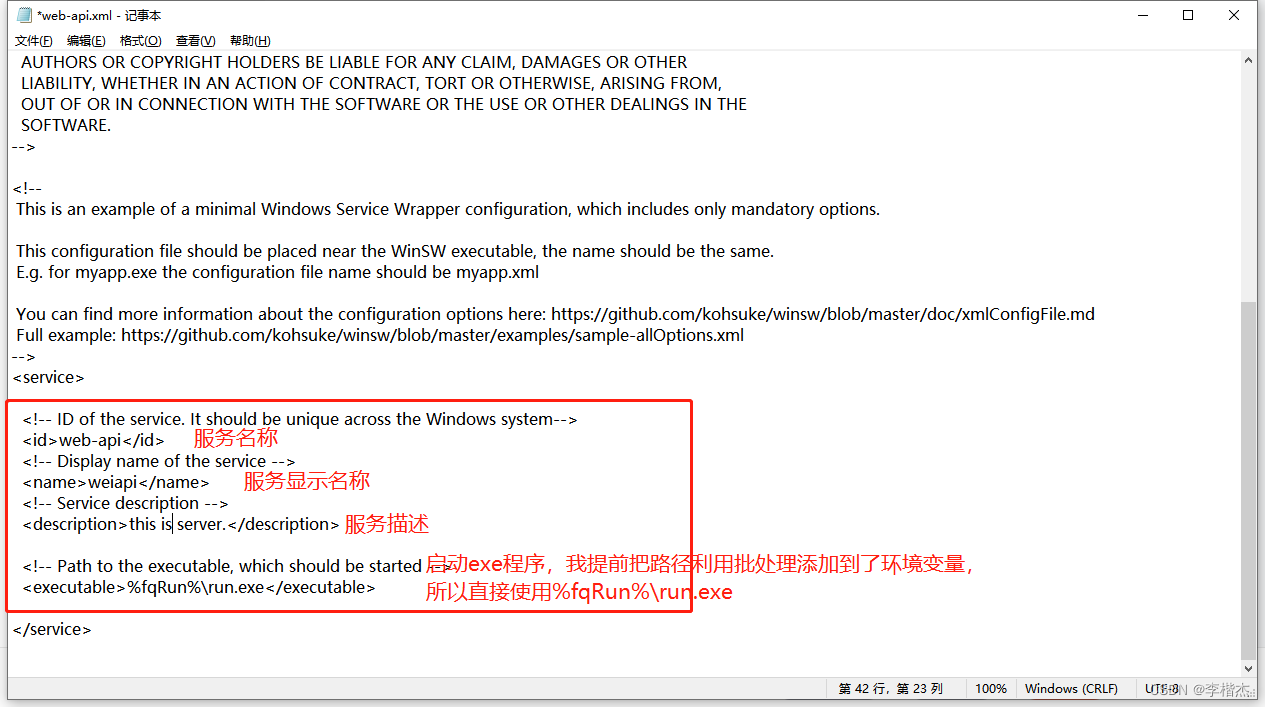
jar包或exe程序设置为windows服务
最近在使用java和python制作客户端时突发奇想,是否能够通过一种方法来讲jar包和exe程序打包成windows服务呢?简单了解了一下是可以的。 首先要用到的是winSW,制作windows服务的过程非常简单,仅需几步制作完成,也不需要…...
数据结构--- 树
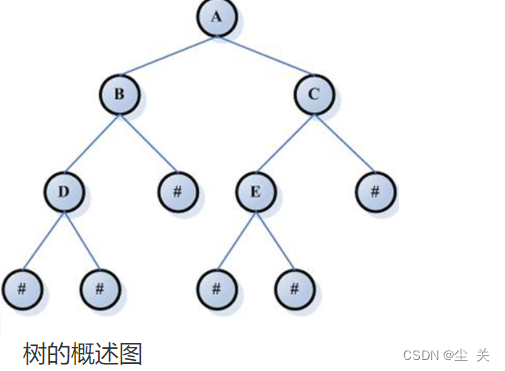
(一)知识补充 定义 树是一种数据结构,它是由n(n≥0)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。 它具有以下的特点: 每个节点有零个或多个子节点; 没有父节点的节点称为根节点;每一个非根…...
两个pdf文件合并为一个怎么操作?分享pdf合并操作步骤
不管是初入职场的小白,还是久经职场的高手,都必须深入了解pdf,特别是关于pdf的各种操作,如编辑、合并、压缩等操作,其中合并是这么多操作里面必需懂的技能之一,但是很多人还是不知道两个pdf文件合并为一个怎…...

Zookeeper简述
数新网络-让每个人享受数据的价值 官网现已全新升级—欢迎访问! 前 言 ZooKeeper是一个开源的、高可用的、分布式的协调服务,由Apache软件基金会维护。它旨在帮助管理和协调分布式系统和应用程序,提供了一个可靠的平台,用于处理…...
1、Flutter移动端App实战教程【环境配置、模拟器配置】
一、概述 Flutter是Google用以帮助开发者在IOS和Android 两个平台开发高质量原生UI的移动SDK,一份代码可以同时生成IOS和Android两个高性能、高保真的应用程序。 二、渲染机制 之所以说Flutter能够达到可以媲美甚至超越原生的体验,主要在于其拥有高性…...
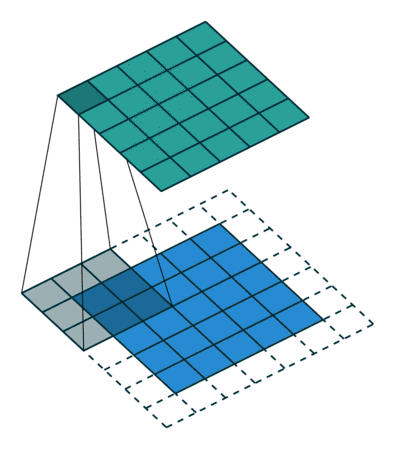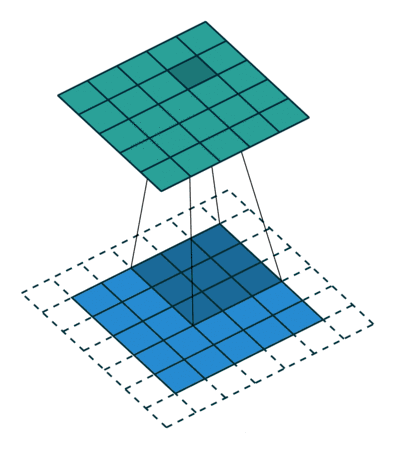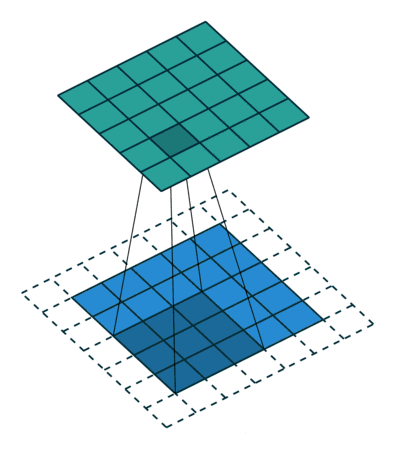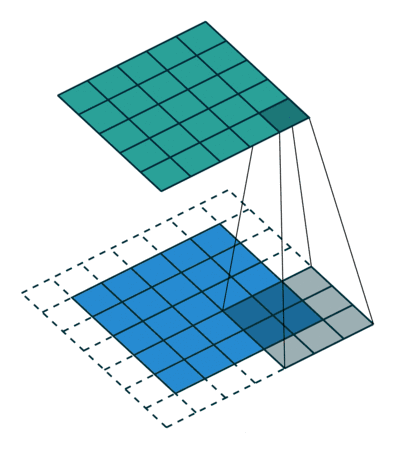
stride与padding对输出尺寸的计算
公式: 练习: 图1: input4,filter3,padding0,stride1 output2 图2: input5,filter3,padding0,stride2 output2 图3: input6,filter3&am…...
Excel VSTO开发2 -建立Excel VSTO项目
版权声明:本文为博主原创文章,转载请在显著位置标明本文出处以及作者网名,未经作者允许不得用于商业目的。 2 建立Excel VSTO项目 新建项目,选择Excel 2013和2016 VSTO外接程序。输入项目名称(本示例的项目名称为&am…...
chrome插件:一个基于webpack + react的chrome 插件项目模板
项目结构 $ tree -L 1 . ├── README.md ├── node_modules # npm依赖 ├── package.json # 详细依赖 ├── pnpm-lock.yaml ├── public # 里边包含dist,安装的时候安装这个目录即可 ├── src …...

Vue:组件缓存
组件缓存 keep-alive 文章目录 组件缓存 keep-alive一、keep-alive是什么二、keep-alive优点三、问题四、解决方案五、代码示例 六、回顾一下钩子七、总结 一、keep-alive是什么 keep-alive是Vue中的一个内置组件,会缓存不活动的组件实例。并不会销毁组件ÿ…...
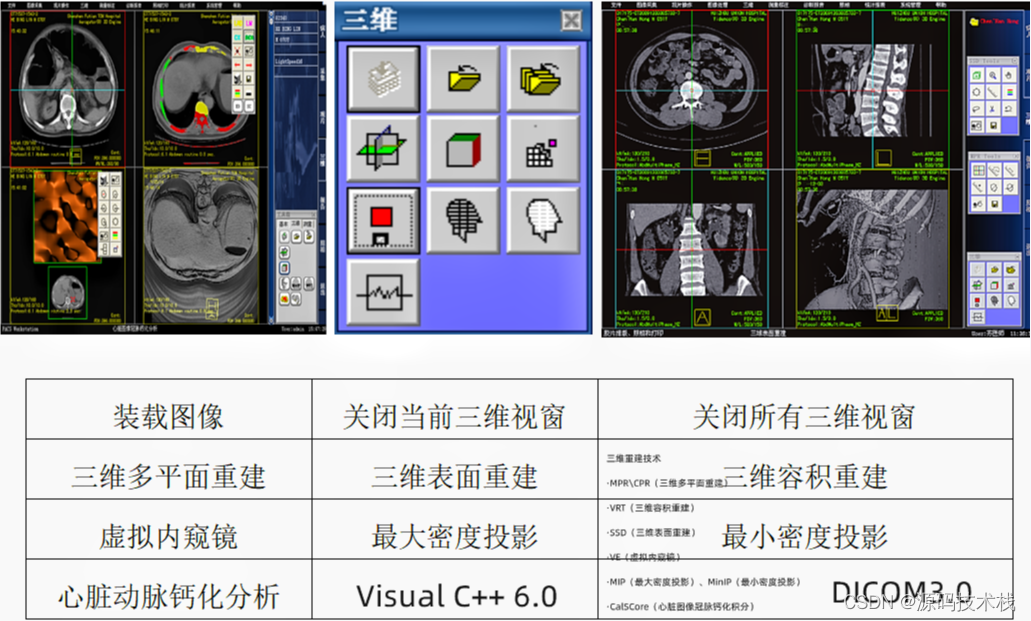
【C++】DICOM医学影像工作站PACS源码
PACS即影像存档与传输系统,是医学影像、数字化图像技术、计算机技术和网络通讯技术相结合的产物,是处理各种医学影像信息的采集、存储、报告、输出、管理、查询的计算机应用程序。 PACS是基于DICOM标准的医学影像管理系统,其模块覆盖了从影像…...

UDP的可靠性传输2
系列文章目录 第一章 UDP的可靠性传输-理论篇(一) 第二章 UDP的可靠性传输-理论篇(二) 文章目录 系列文章目录三、流量控制RTORTT流量控制1.如何控制流量2. 发送方何时在发送数据3.流程图 拥塞控制1.慢启动 总结1.拥塞控制和流量…...

《Java程序设计》实验报告
实验内容:面向对象程序设计 1、定一个名为Person的类,其中含有一个String类型的成员变量name和一个int类型的成员变量age, 分别为这两个变量定义访问方法和修改方法,另外再为该类定义一个名为speak的方法, 在其中输出n…...

数据可视化、BI和数字孪生软件:用途和特点对比
在现代企业和科技领域,数据起着至关重要的作用。为了更好地管理和理解数据,不同类型的软件工具应运而生,其中包括数据可视化软件、BI(Business Intelligence)软件和数字孪生软件。虽然它们都涉及数据,但在功…...
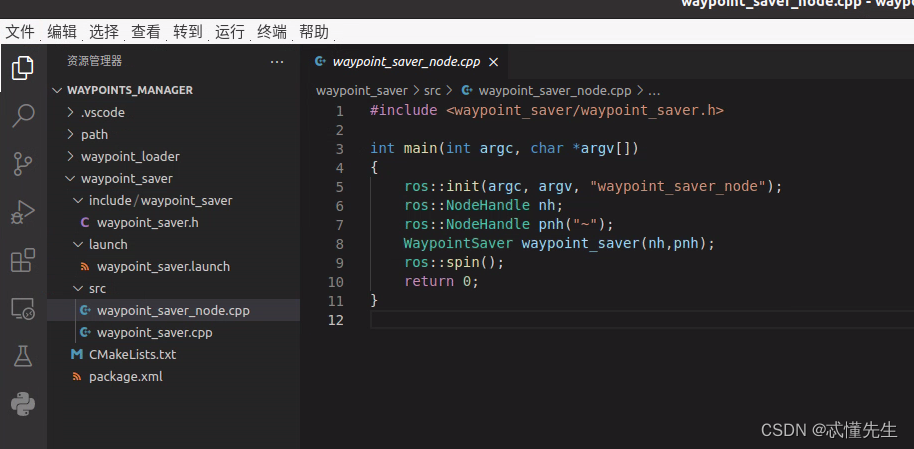
Ros noetic 机器人坐标记录运动路径和发布 实战教程(C)
前言: 承接上一篇博文本文将编写并记录上文中详细的工程项目,用于保存小车的运动路径,生成对应的csv,和加载所保存的路径到实际的Rviz中,本文将开源完整的工程项目,工程结构如下: 工程原码位于文章末尾: 路径存储: waypoint_saver 用于存储 waypoint 的节点 waypo…...

【Oracle APEX开发小技巧12】
有如下需求: 有一个问题反馈页面,要实现在apex页面展示能直观看到反馈时间超过7天未处理的数据,方便管理员及时处理反馈。 我的方法:直接将逻辑写在SQL中,这样可以直接在页面展示 完整代码: SELECTSF.FE…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

Python ROS2【机器人中间件框架】 简介
销量过万TEEIS德国护膝夏天用薄款 优惠券冠生园 百花蜂蜜428g 挤压瓶纯蜂蜜巨奇严选 鞋子除臭剂360ml 多芬身体磨砂膏280g健70%-75%酒精消毒棉片湿巾1418cm 80片/袋3袋大包清洁食品用消毒 优惠券AIMORNY52朵红玫瑰永生香皂花同城配送非鲜花七夕情人节生日礼物送女友 热卖妙洁棉…...

LeetCode - 199. 二叉树的右视图
题目 199. 二叉树的右视图 - 力扣(LeetCode) 思路 右视图是指从树的右侧看,对于每一层,只能看到该层最右边的节点。实现思路是: 使用深度优先搜索(DFS)按照"根-右-左"的顺序遍历树记录每个节点的深度对于…...

基于 TAPD 进行项目管理
起因 自己写了个小工具,仓库用的Github。之前在用markdown进行需求管理,现在随着功能的增加,感觉有点难以管理了,所以用TAPD这个工具进行需求、Bug管理。 操作流程 注册 TAPD,需要提供一个企业名新建一个项目&#…...

go 里面的指针
指针 在 Go 中,指针(pointer)是一个变量的内存地址,就像 C 语言那样: a : 10 p : &a // p 是一个指向 a 的指针 fmt.Println(*p) // 输出 10,通过指针解引用• &a 表示获取变量 a 的地址 p 表示…...

离线语音识别方案分析
随着人工智能技术的不断发展,语音识别技术也得到了广泛的应用,从智能家居到车载系统,语音识别正在改变我们与设备的交互方式。尤其是离线语音识别,由于其在没有网络连接的情况下仍然能提供稳定、准确的语音处理能力,广…...

Modbus RTU与Modbus TCP详解指南
目录 1. Modbus协议基础 1.1 什么是Modbus? 1.2 Modbus协议历史 1.3 Modbus协议族 1.4 Modbus通信模型 🎭 主从架构 🔄 请求响应模式 2. Modbus RTU详解 2.1 RTU是什么? 2.2 RTU物理层 🔌 连接方式 ⚡ 通信参数 2.3 RTU数据帧格式 📦 帧结构详解 🔍…...
