deepfm内容理解
对于CTR问题,被证明的最有效的提升任务表现的策略是特征组合(Feature Interaction);
两个问题:
如何更好地学习特征组合,进而更加精确地描述数据的特点;
如何更高效的学习特征组合。
DNN局限 :当我们使用DNN网络解决推荐问题的时候存在网络参数过于庞大的问题,这是因为在进行特征处理的时候我们需要使用one-hot编码来处理离散特征,这会导致输入的维度猛增。
为了解决DNN参数量过大的局限性,可以采用非常经典的Field思想,将OneHot特征转换为Dense Vector,通过增加全连接层就可以实现高阶的特征组合。
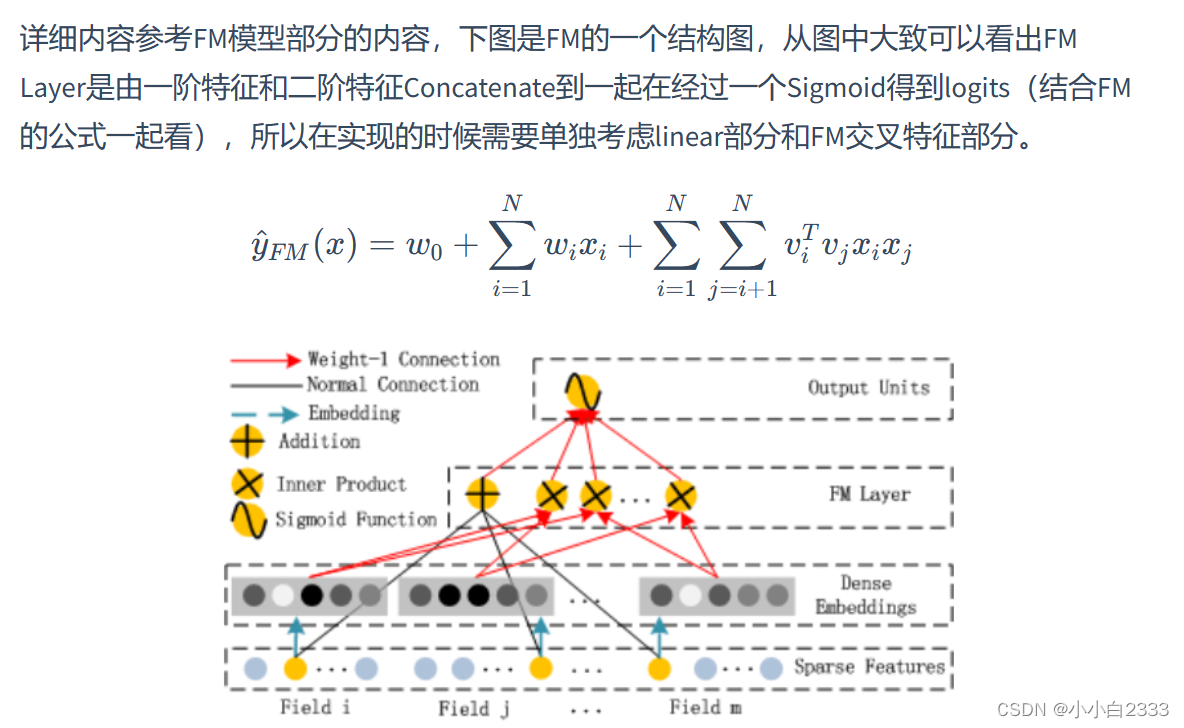
黑色的线 和 红色的线 进行concat
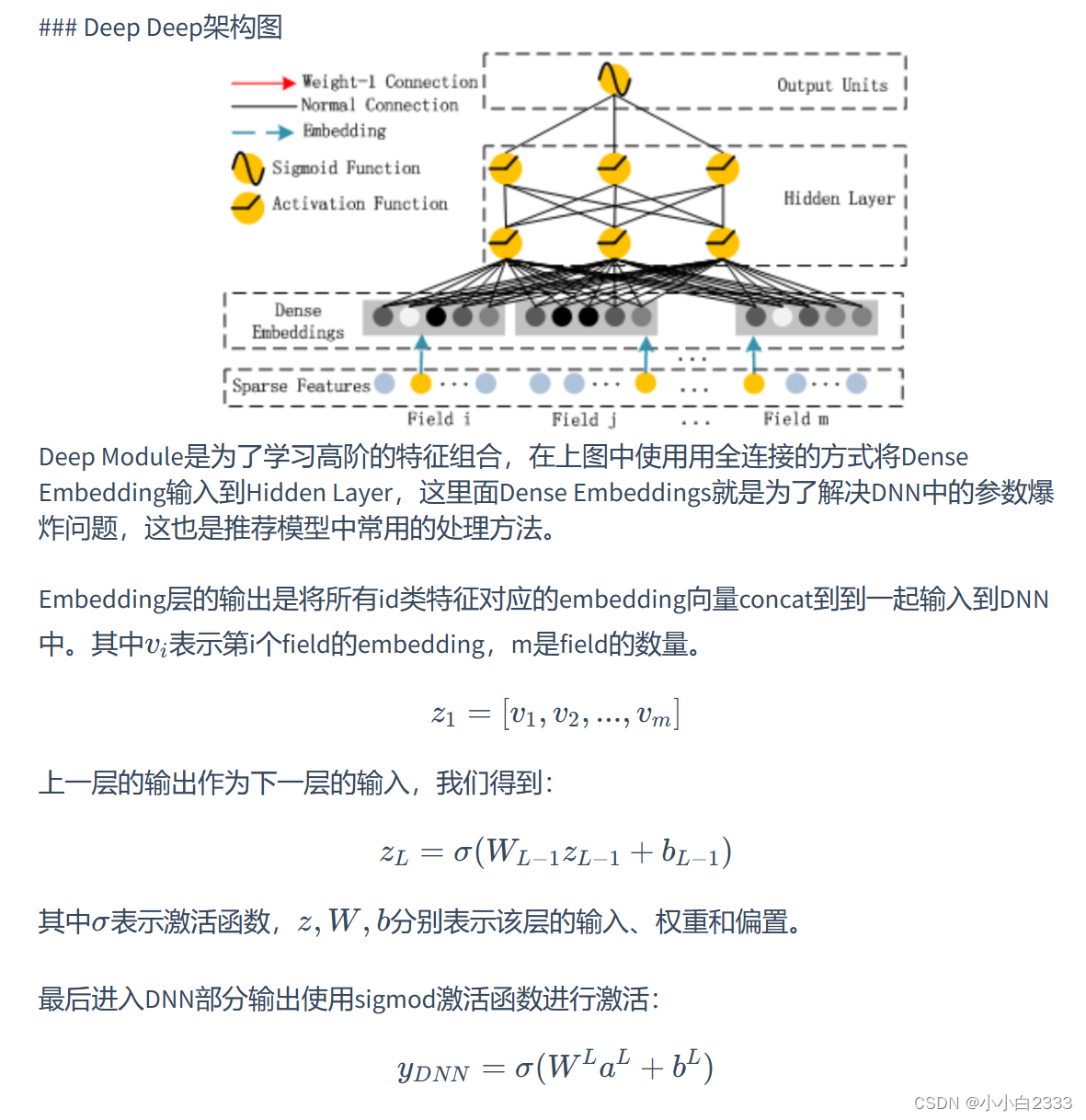
self定义
deep_features = deep_features
fm_features = fm_features #稀疏的特征
deep_dims = sum([fea.embed_dim for fea in deep_features]) #8
fm_dims = sum([fea.embed_dim for fea in fm_features]) #368 = 23*16 #稀疏的特征embedding化
linear = LR(fm_dims) # 1-odrder interaction 低阶信息 (fc): Linear(in_features=368, out_features=1, bias=True)
fm = FM(reduce_sum=True) # 2-odrder interaction #FM将一阶特征和二阶特征cancat
embedding = EmbeddingLayer(deep_features + fm_features)
mlp = MLP(deep_dims, **mlp_params)
forward
input_deep = embedding(x, deep_features, squeeze_dim=True) #[batch_size, deep_dims] torch.Size([10, 8])
input_fm = embedding(x, fm_features, squeeze_dim=False) #[batch_size, num_fields, embed_dim] torch.Size([10, 23, 16])
y_linear = linear(input_fm.flatten(start_dim=1)) #torch.Size([10, 1]) 对应的稀疏特征 经过线性层变为1
y_fm = fm(input_fm) #torch.Size([10, 1]) #对稀疏特征做一阶 二阶处理
y_deep = mlp(input_deep) #[batch_size, 1] #torch.Size([10, 1])
y = y_linear + y_fm + y_deep
# return torch.sigmoid(y.squeeze(1))
定义的一些函数:
import torch.nn as nn
class LR(nn.Module):
"""Logistic Regression Module. It is the one Non-linear
transformation for input feature.Args:
input_dim (int): input size of Linear module.
sigmoid (bool): whether to add sigmoid function before output.Shape:
- Input: `(batch_size, input_dim)`
- Output: `(batch_size, 1)`
"""def __init__(self, input_dim, sigmoid=False):
super().__init__()
self.sigmoid = sigmoid
self.fc = nn.Linear(input_dim, 1, bias=True)def forward(self, x):
if self.sigmoid:
return torch.sigmoid(self.fc(x))
else:
return self.fc(x)
class FM(nn.Module):
"""The Factorization Machine module, mentioned in the `DeepFM paper
<https://arxiv.org/pdf/1703.04247.pdf>`. It is used to learn 2nd-order
feature interactions.Args:
reduce_sum (bool): whether to sum in embed_dim (default = `True`).Shape:
- Input: `(batch_size, num_features, embed_dim)`
- Output: `(batch_size, 1)`` or ``(batch_size, embed_dim)`
"""def __init__(self, reduce_sum=True):
super().__init__()
self.reduce_sum = reduce_sumdef forward(self, x):
square_of_sum = torch.sum(x, dim=1)**2
sum_of_square = torch.sum(x**2, dim=1)
ix = square_of_sum - sum_of_square
if self.reduce_sum:
ix = torch.sum(ix, dim=1, keepdim=True)
return 0.5 * ix
参考资料:
推荐系统遇上深度学习(三)--DeepFM模型理论和实践 - 简书 (jianshu.com)
DeepFM (datawhalechina.github.io)
相关文章:

deepfm内容理解
对于CTR问题,被证明的最有效的提升任务表现的策略是特征组合(Feature Interaction); 两个问题: 如何更好地学习特征组合,进而更加精确地描述数据的特点; 如何更高效的学习特征组合。 DNN局限 :当我们使…...
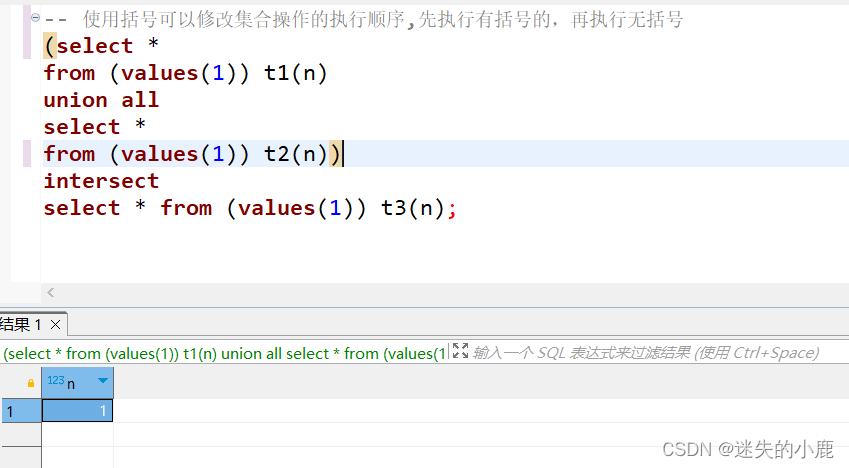
postgresql-集合运算
postgresql-集合运算 并集交集差集集合运算符的优先级 并集 create table excellent_emp( year int not null, emp_id integer not null, constraint pk_excellent_emp primary key(year,emp_id) );insert into excellent_emp values(2018,9); insert into excellent_emp value…...

[持续更新]计算机经典面试题基础篇Day2
[通用]计算机经典面试题基础篇Day2 1、单例模式是什么,线程安全吗 单例模式是一种设计模式,旨在确保一个类只有一个实例,并提供全局访问点。通过使用单例模式,可以避免多次创建相同的对象,节省内存资源,同…...

C++:类和对象(二)
本文主要介绍:构造函数、析构函数、拷贝构造函数、赋值运算符重载、const成员函数、取地址及const取地址操作符重载。 目录 一、类的六个默认成员函数 二、构造函数 1.概念 2.特性 三、析构函数 1.概念 2.特性 四、拷贝构造函数 1.概念 2.特征 五、赋值…...
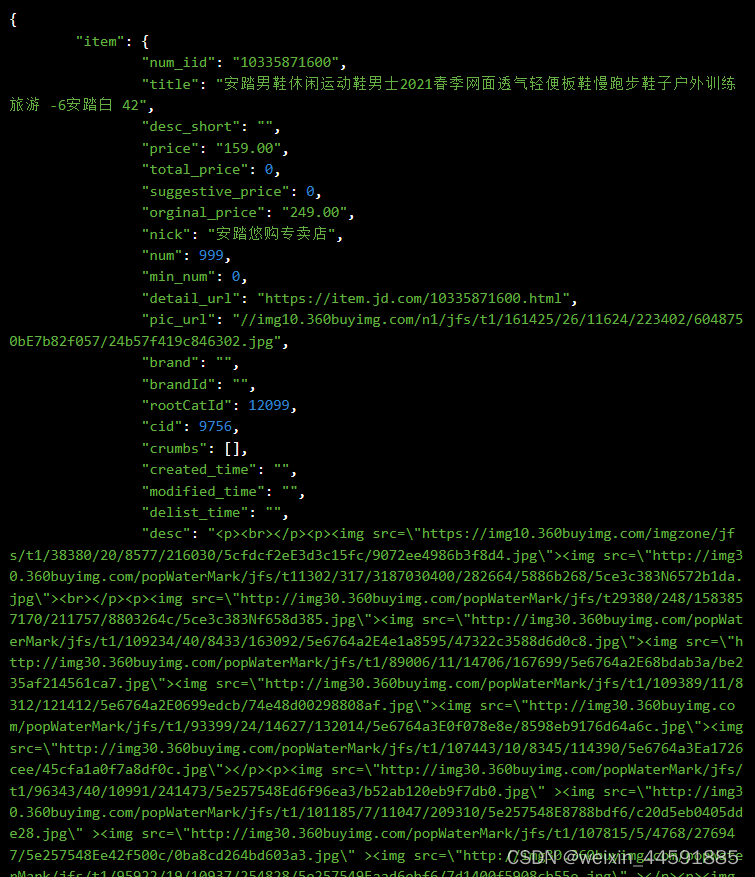
Java“牵手”京东商品详情数据,京东商品详情API接口,京东API接口申请指南
京东平台商品详情接口是开放平台提供的一种API接口,通过调用API接口,开发者可以获取京东商品的标题、价格、库存、月销量、总销量、库存、详情描述、图片等详细信息 。 获取商品详情接口API是一种用于获取电商平台上商品详情数据的接口,通过…...

Fluidd摄像头公网无法正常显示修复一例
Fluidd摄像头在内网正常显示,公网一直无法显示,经过排查发现由于url加了端口号引起的,摄像头url中正常填写的是/webcam?actionsnapshot,或者/webcam?actionstream。但是由于nginx跳转机制,会被301跳转到/webcam/?ac…...
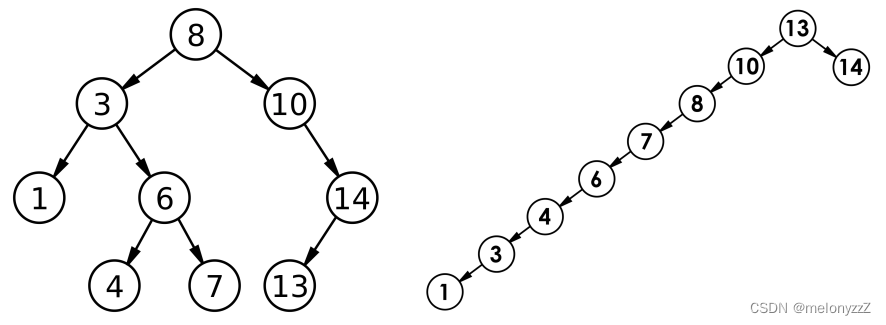
【C++ 学习 ⑳】- 详解二叉搜索树
目录 一、概念 二、实现 2.1 - BST.h 2.2 - test.cpp 三、应用 四、性能分析 一、概念 二叉搜索树(BST,Binary Search Tree),又称二叉排序树或二叉查找树。 二叉搜索树是一棵二叉树,可以为空;如果不…...
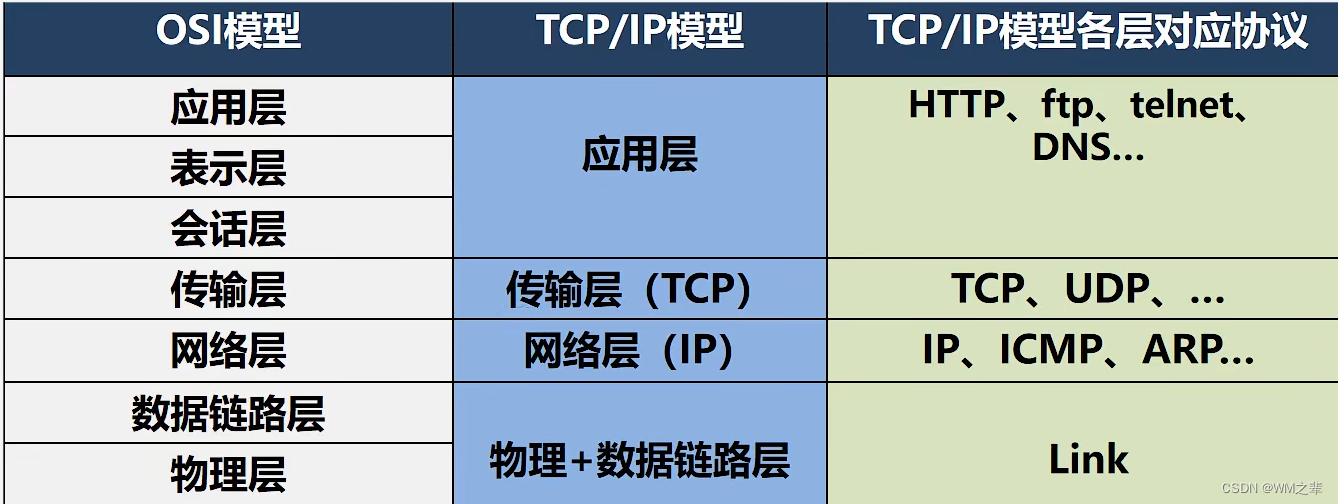
Java中网络的基本介绍。网络通信,网络,ip地址,域名,端口,网络通信协议,TCP/IP传输过程,网络通信协议模型,TCP协议,UDP协议
- 网络通信 概念:网络通信是指通过计算机网络进行信息传输的过程,包括数据传输、语音通话、视频会议等。在网络通信中,数据被分成一系列的数据包,并通过网络传输到目的地。在数据传输过程中,需要确保数据的完整性、准…...

【Qt】总体把握文本编码问题
在项目开发中,经常会遇到文本编码问题。文本编码知识非常基础,但对于新手来说,可能需要花费较长的时间去尝试,才能在脑海中建立对编码的正确认知。文本编码原理并不难,难的是在项目实践中掌握正确处理文本编码的方法。…...
之curl)
Linux命令(77)之curl
linux命令之curl 1.curl介绍 linux命令之curl是一款强大的http命令行工具,它支持文件的上传和下载,是综合传输工具。 2.curl用法 curl [参数] [url] curl参数 参数说明-C断点续传-o <filename>把输出写到filename文件中-x在给定的端口上使用HT…...

详解 sudo usermod -aG docker majn
这个命令涉及到几个 Linux 系统管理的基础概念,包括 sudo、usermod 和用户组管理。我们可以逐一地解析它们: sudo: sudo(superuser do)允许一个已经被授权的用户以超级用户或其他用户的身份执行一个命令。当使用 sudo 前缀一个命令…...
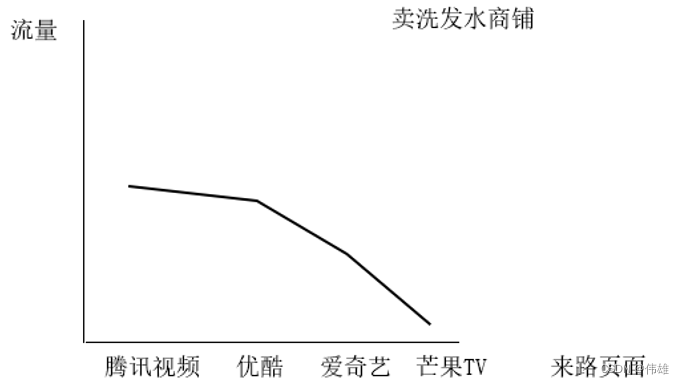
大数据课程L2——网站流量项目的算法分析数据处理
文章作者邮箱:yugongshiye@sina.cn 地址:广东惠州 ▲ 本章节目的 ⚪ 了解网站流量项目的算法分析; ⚪ 了解网站流量项目的数据处理; 一、项目的算法分析 1. 概述 网站流量统计是改进网站服务的重要手段之一,通过获取用户在网站的行为,可以分析出哪些内…...
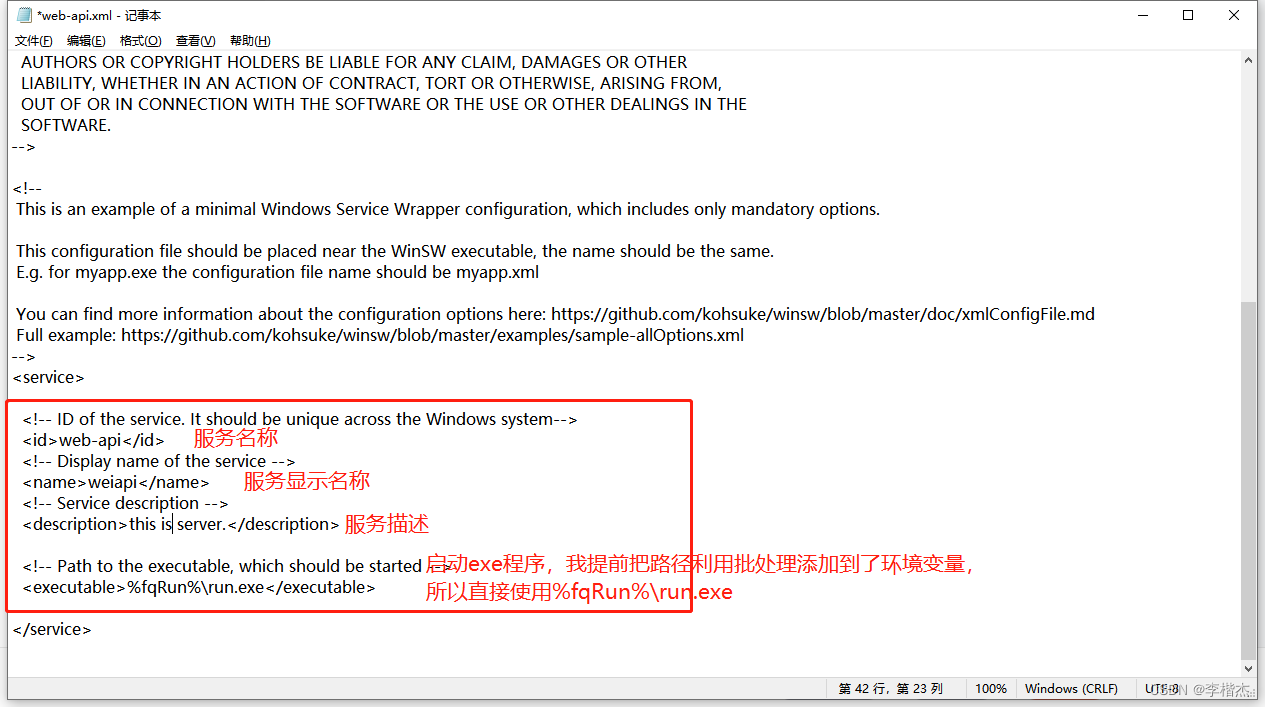
jar包或exe程序设置为windows服务
最近在使用java和python制作客户端时突发奇想,是否能够通过一种方法来讲jar包和exe程序打包成windows服务呢?简单了解了一下是可以的。 首先要用到的是winSW,制作windows服务的过程非常简单,仅需几步制作完成,也不需要…...
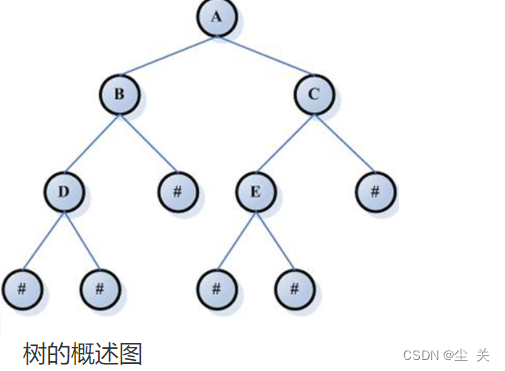
数据结构--- 树
(一)知识补充 定义 树是一种数据结构,它是由n(n≥0)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。 它具有以下的特点: 每个节点有零个或多个子节点; 没有父节点的节点称为根节点;每一个非根…...
两个pdf文件合并为一个怎么操作?分享pdf合并操作步骤
不管是初入职场的小白,还是久经职场的高手,都必须深入了解pdf,特别是关于pdf的各种操作,如编辑、合并、压缩等操作,其中合并是这么多操作里面必需懂的技能之一,但是很多人还是不知道两个pdf文件合并为一个怎…...

Zookeeper简述
数新网络-让每个人享受数据的价值 官网现已全新升级—欢迎访问! 前 言 ZooKeeper是一个开源的、高可用的、分布式的协调服务,由Apache软件基金会维护。它旨在帮助管理和协调分布式系统和应用程序,提供了一个可靠的平台,用于处理…...
1、Flutter移动端App实战教程【环境配置、模拟器配置】
一、概述 Flutter是Google用以帮助开发者在IOS和Android 两个平台开发高质量原生UI的移动SDK,一份代码可以同时生成IOS和Android两个高性能、高保真的应用程序。 二、渲染机制 之所以说Flutter能够达到可以媲美甚至超越原生的体验,主要在于其拥有高性…...
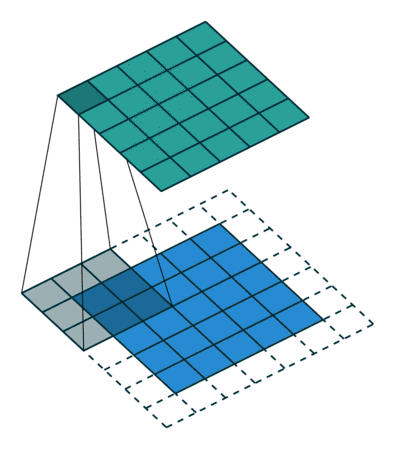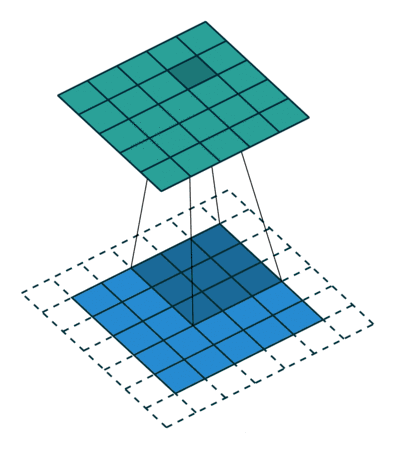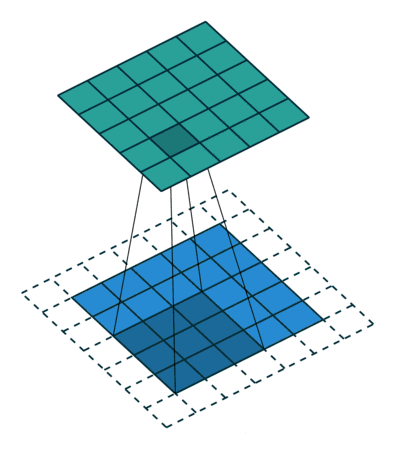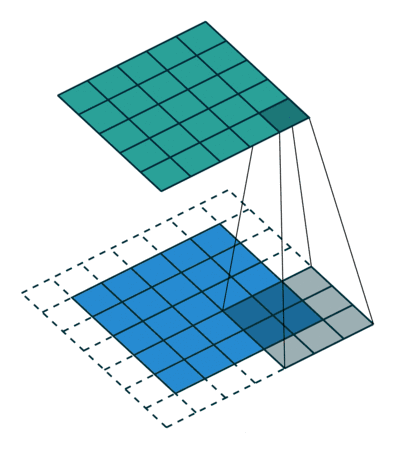
stride与padding对输出尺寸的计算
公式: 练习: 图1: input4,filter3,padding0,stride1 output2 图2: input5,filter3,padding0,stride2 output2 图3: input6,filter3&am…...
Excel VSTO开发2 -建立Excel VSTO项目
版权声明:本文为博主原创文章,转载请在显著位置标明本文出处以及作者网名,未经作者允许不得用于商业目的。 2 建立Excel VSTO项目 新建项目,选择Excel 2013和2016 VSTO外接程序。输入项目名称(本示例的项目名称为&am…...
chrome插件:一个基于webpack + react的chrome 插件项目模板
项目结构 $ tree -L 1 . ├── README.md ├── node_modules # npm依赖 ├── package.json # 详细依赖 ├── pnpm-lock.yaml ├── public # 里边包含dist,安装的时候安装这个目录即可 ├── src …...

Vim 调用外部命令学习笔记
Vim 外部命令集成完全指南 文章目录 Vim 外部命令集成完全指南核心概念理解命令语法解析语法对比 常用外部命令详解文本排序与去重文本筛选与搜索高级 grep 搜索技巧文本替换与编辑字符处理高级文本处理编程语言处理其他实用命令 范围操作示例指定行范围处理复合命令示例 实用技…...

Leetcode 3576. Transform Array to All Equal Elements
Leetcode 3576. Transform Array to All Equal Elements 1. 解题思路2. 代码实现 题目链接:3576. Transform Array to All Equal Elements 1. 解题思路 这一题思路上就是分别考察一下是否能将其转化为全1或者全-1数组即可。 至于每一种情况是否可以达到…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

【HarmonyOS 5.0】DevEco Testing:鸿蒙应用质量保障的终极武器
——全方位测试解决方案与代码实战 一、工具定位与核心能力 DevEco Testing是HarmonyOS官方推出的一体化测试平台,覆盖应用全生命周期测试需求,主要提供五大核心能力: 测试类型检测目标关键指标功能体验基…...

STM32+rt-thread判断是否联网
一、根据NETDEV_FLAG_INTERNET_UP位判断 static bool is_conncected(void) {struct netdev *dev RT_NULL;dev netdev_get_first_by_flags(NETDEV_FLAG_INTERNET_UP);if (dev RT_NULL){printf("wait netdev internet up...");return false;}else{printf("loc…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

vue3 定时器-定义全局方法 vue+ts
1.创建ts文件 路径:src/utils/timer.ts 完整代码: import { onUnmounted } from vuetype TimerCallback (...args: any[]) > voidexport function useGlobalTimer() {const timers: Map<number, NodeJS.Timeout> new Map()// 创建定时器con…...

Linux-07 ubuntu 的 chrome 启动不了
文章目录 问题原因解决步骤一、卸载旧版chrome二、重新安装chorme三、启动不了,报错如下四、启动不了,解决如下 总结 问题原因 在应用中可以看到chrome,但是打不开(说明:原来的ubuntu系统出问题了,这个是备用的硬盘&a…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...
