Python_操作记录
1、Pandas读取数据文件(以文本文件作为示例),sep表示间隔,header=None表示无标题行
df = pd.read_table("data/youcans3.dat", sep="\t", header=None)2、线性规划问题求解
1)问题定义,确定决策变量、目标函数和约束条件;
2)模型构建,由问题描述建立数学方程,并转化为标准形式的数学模型;
3)模型求解,用标准模型的优化算法对模型求解,得到优化结果。
很多Python的第三方包,都提供求解线性规划问题的算法,有的工具包还提供证书规划、非线性规划的算法,例如:
1)Scipy提供了了解简单线性或非线性规划问题,但是不能求解如背包问题的0-1规划问题,或整数规划问题,混合整数规划问题。
2)PuLP可以求解线性规划、整数规划、0-1规划、混合整数规划、二次规划和几何规划问题
2.1 PuLP库求解线性规划问题
import pulp
#1、定义一个规划问题,Demo表示问题名称,sense表示最大/最小参数(LpMinimize、LpMaximize)
m = pulp.LpProblem("Demo", sense=pulp.LpMaximize)
#定义决策变量(名称,上限,下限,参数)
#2、cat来设置变量类型,'Continuous'表示连续变量(默认值),'Integer'表示离散变量,'Binary'表示0/1变量
x1 = pulp.LpVariable('x1',lowBound=0,upBound=7,cat='Continuous')
x2 = pulp.LpVariable('x2',lowBound=0,upBound=7,cat='Continuous')
x3 = pulp.LpVariable('x3',lowBound=0,upBound=7,cat='Continuous')
#3、添加目标函数
m += 2*x1 + 3*x2 - 5*x3
#4、添加约束条件
m += (2*x1 - 5*x2 + x3 >= 10)
m += (x1 + 3*x2 + x3 <= 12)
m += (x1 + x2 + x3 == 7)
#5、求解
m.solve()
print("Satus:",pulp.LpStatus[m.status]) #输出求解状态
for v in m.variables():print(v.name,"=",v.varValue) #输出每个变量的最优值
print("F(x) = ",pulp.value(m.objective)) #输出最优解的目标函数值相关文章:

Python_操作记录
1、Pandas读取数据文件(以文本文件作为示例),sep表示间隔,headerNone表示无标题行 df pd.read_table("data/youcans3.dat", sep"\t", headerNone) 2、线性规划问题求解 1)问题定义,…...

常用激活函数整理
最近一边应付工作,一边在补足人工智能的一些基础知识,这个方向虽然新兴,但已是卷帙浩繁,有时不知从何入手,幸亏有个适合基础薄弱的人士学习的网站,每天学习一点,积跬步以至千里吧。有像我一样学…...

uniapp 地图跳转到第三方导航软件 直接打包成apk
// 判断是否存在导航软件judgeHasExistNavignation() {let navAppParam [{pname: com.baidu.BaiduMap,action: baidumap://}, // 百度{pname: com.autonavi.minimap,action: iosamap://}, // 高德{pname: com.tencent.map,action: tencentmap://}, // 腾讯];return navAppPara…...

CentOS 8 通过YUM方式升级最新内核
CentOS 8 通过YUM方式升级最新内核 查看当前内核 uname -r 4.18.0-193.6.3.el8_2.x86_64导入 ELRepo 仓库的公钥: rpm --import https://www.elrepo.org/RPM-GPG-KEY-elrepo.org安装升级内核相关的yum源仓库(安装 ELRepo 仓库的 yum 源) yum install https://www…...

java 版本企业招标投标管理系统源码+功能描述+tbms+及时准确+全程电子化
功能描述 1、门户管理:所有用户可在门户页面查看所有的公告信息及相关的通知信息。主要板块包含:招标公告、非招标公告、系统通知、政策法规。 2、立项管理:企业用户可对需要采购的项目进行立项申请,并提交审批,查看所…...

Python爬虫数据存哪里|数据存储到文件的几种方式
前言 大家早好、午好、晚好吖 ❤ ~欢迎光临本文章 爬虫请求解析后的数据,需要保存下来,才能进行下一步的处理,一般保存数据的方式有如下几种: 文件:txt、csv、excel、json等,保存数据量小。 关系型数据库…...
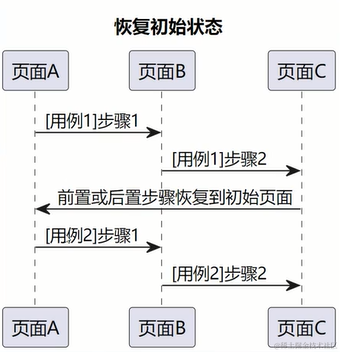
软件测试/测试开发丨Web自动化 测试用例流程设计
点此获取更多相关资料 本文为霍格沃兹测试开发学社学员学习笔记分享 原文链接:https://ceshiren.com/t/topic/27173 一、测试用例通用结构回顾 1.1、现有测试用例存在的问题 可维护性差可读性差稳定性差 1.2、用例结构设计 测试用例的编排测试用例的项目结构 1…...

git撤销修改命令
要撤销Git中尚未提交的所有修改,可以使用以下几种方法: 1、使用git checkout命令丢弃工作目录的修改,重置工作目录中所有文件的修改。 git checkout . 2、使用git reset命令重置暂存区和工作目录, 重置暂存区和工作目录,回到最后一次提交后的状态。 …...

EOCR-AR电机保护器自动复位的启用条件说明
为适用不同的现场使用需求,施耐德韩国公司推出了带有自动复位功能的模拟型电动机保护器-EOCR-AR。EOCR-AR电机保护器具有过电流、缺相、堵转保护功能,还可根据实际需要设置自动复位时间。 EOCR-AR自动复位的设置方法 如上图,R-TIME旋钮是自动…...
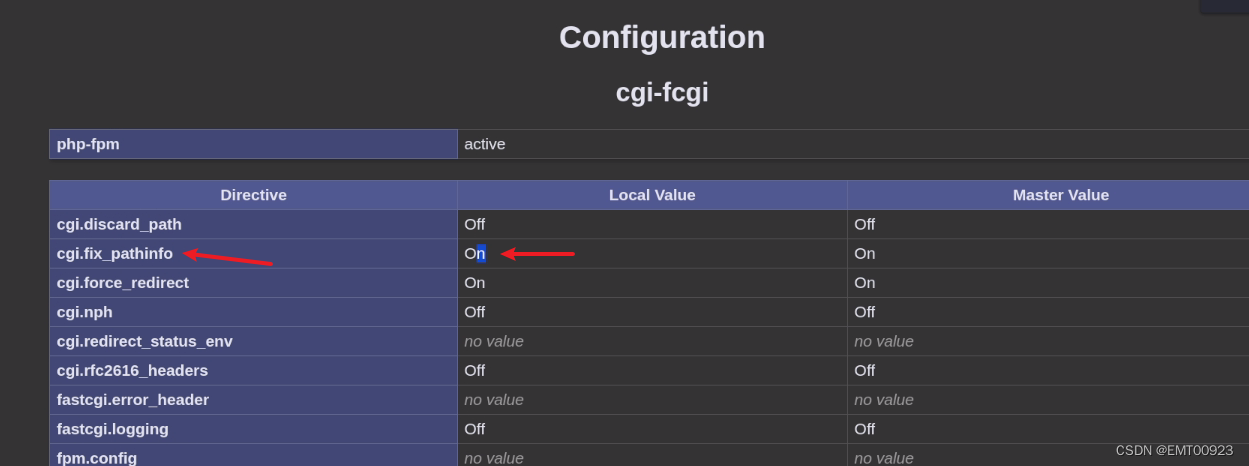
Apache nginx解析漏洞复现
文章目录 空字节漏洞安装环境漏洞复现 背锅解析漏洞安装环境漏洞复现 空字节漏洞 安装环境 将nginx解压后放到c盘根目录下: 运行startup.bat启动环境: 在HTML文件夹下有它的主页文件: 漏洞复现 nginx在遇到后缀名有php的文件时,…...
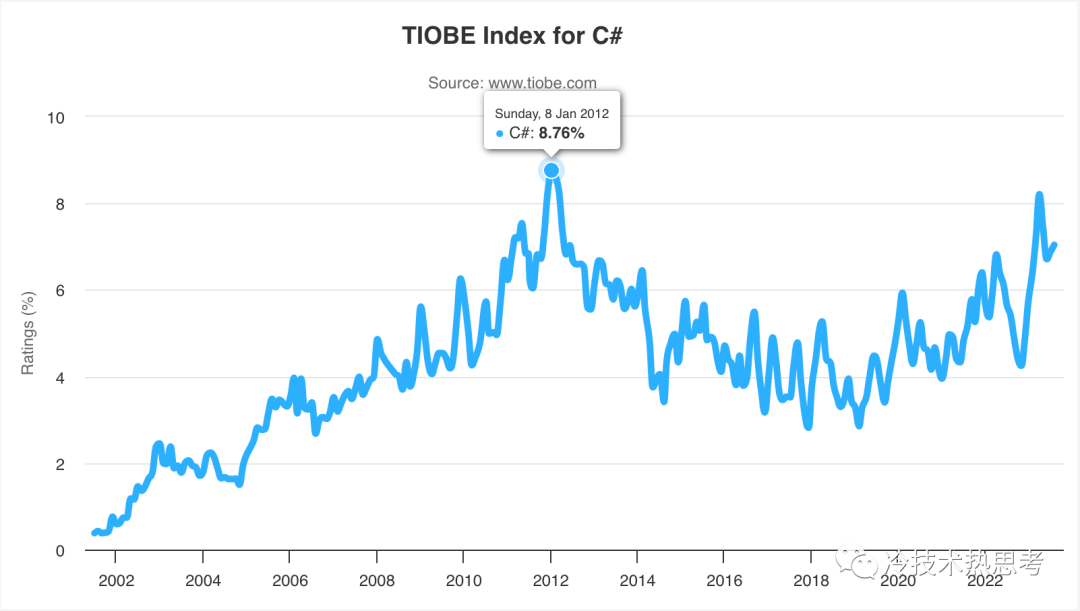
.NET之后,再无大创新
回想起来,2001年发布的.NET已经是距离最近的一次软件开发技术的整体创新了,后续的新技术就没有在各个端都这么成功的了。.NET是Windows平台下软件开发技术的巨大变革。在此之前,有VB、C(MFC)、JSP,在此之后…...

【大麦小米学量化】什么是量化交易?哪些人适合做量化交易?
系列文章目录 文章目录 系列文章目录学霸的梦想前言一、什么是量化交易?二、哪些人适合做量化交易?三、量化交易都需要掌握哪些技术和方法?总结 学霸的梦想 小米支棱着迷糊的眼睛,一脸懵逼的问大麦:“我说大麦哥哥&…...
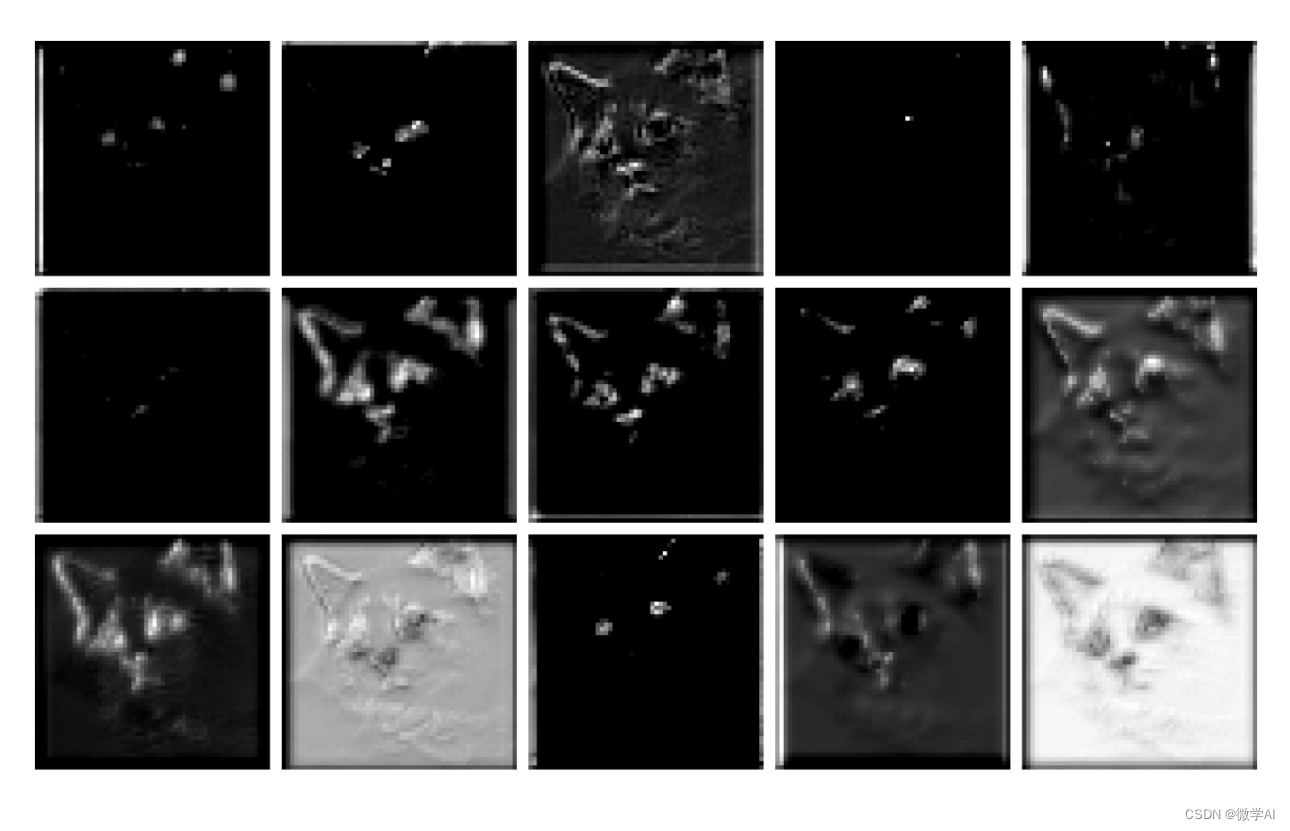
计算机视觉的应用12-卷积神经网络中图像特征提取的可视化研究,让大家理解特征提取的全过程
大家好,我是微学AI,今天给大家介绍一下计算机视觉的应用12-卷积神经网络中图像特征提取的可视化研究,让大家理解特征提取的全过程。 要理解卷积神经网络中图像特征提取的全过程,我们可以将其比喻为人脑对视觉信息的处理过程。就像…...
el-table中点击跳转到详情页的两种方法
跳转的两种写法: 1.使用keep-alive使组件缓存,防止刷新时参数丢失 keep-alive 组件用于缓存和保持组件的状态,而不是路由参数。它可以在组件切换时保留组件的状态,从而避免重新渲染和加载数据。 keep-alive 主要用于提高页面性能和用户体验,而…...
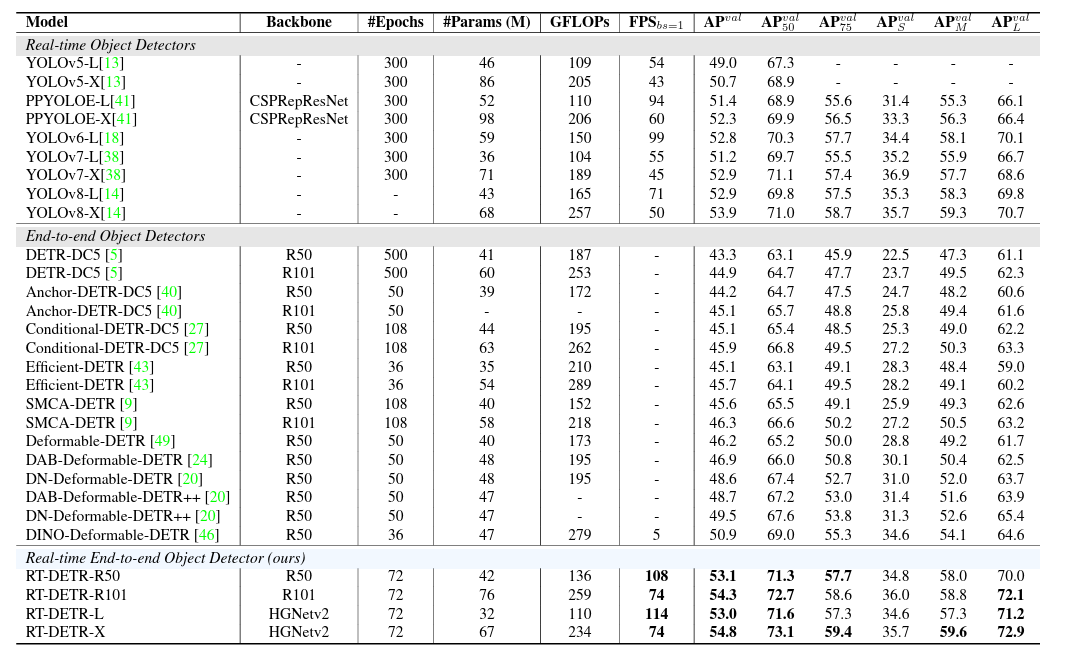
RT-DETR个人整理向理解
一、前言 在开始介绍RT-DETR这个网络之前,我们首先需要先了解DETR这个系列的网络与我们常提及的anchor-base以及anchor-free存在着何种差异。 首先我们先简单讨论一下anchor-base以及anchor-free两者的差异与共性: 1、两者差异:顾名思义&…...

易点易动库存管理系统与ERP系统打通,帮助企业实现低值易耗品管理
现今,企业管理日趋复杂,无论是核心经营还是辅助环节,都需要依靠信息化手段来提升效率。而低值易耗品作为企业日常运营中的必需品,其管理也面临诸多挑战。传统做法效率低下,容易出错。如何通过信息化手段实现低值易耗品的高效管理,成为许多企业必顾及的一个课题。 易点易动作为…...

【笔试强训选择题】Day34.习题(错题)解析
作者简介:大家好,我是未央; 博客首页:未央.303 系列专栏:笔试强训选择题 每日一句:人的一生,可以有所作为的时机只有一次,那就是现在!!!ÿ…...

“现代”“修饰”卷积神经网络,何谓现代
一、“现代” vs “传统” 现代卷积神经网络(CNNs)与传统卷积神经网络之间存在一些关键区别。这些区别主要涉及网络的深度、结构、训练技巧和应用领域等方面。以下是现代CNNs与传统CNNs之间的一些区别: 深度: 传统CNNs࿱…...

XHTML基础知识了解
XHTML是一种严格符合XML规范的标记语言,它的基本语法和HTML类似,但是更加严谨和规范。XHTML的代码结构非常清晰,方便浏览器和搜索引擎解析。下面是一些XHTML的基础知识和代码示例: 声明文档类型(DTD) 在X…...
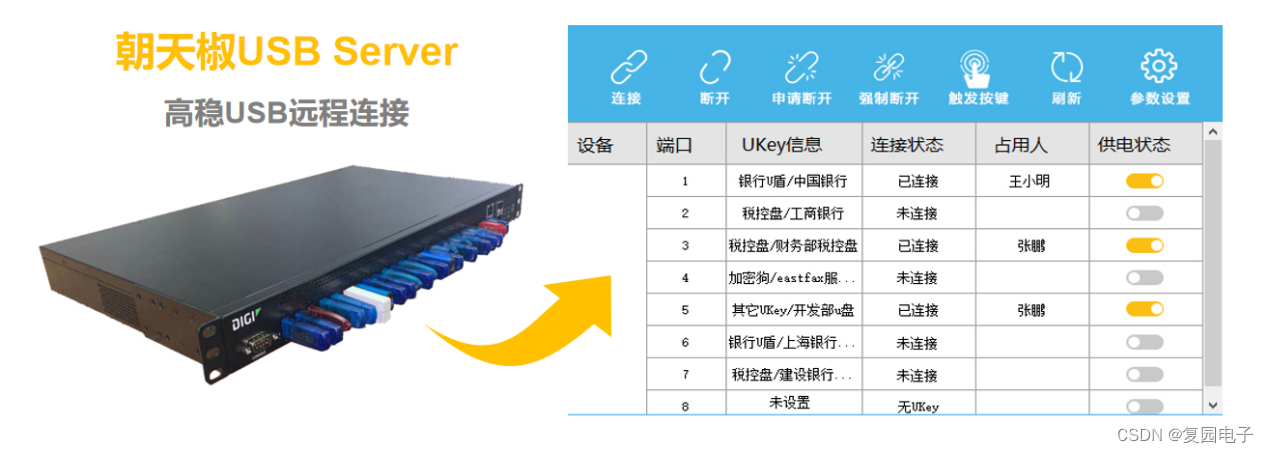
USB Server集中管控加密狗,浙江省电力设计院正在用
近日,软件加密狗的分散管理和易丢失性,给拥有大量加密狗的浙江省电力设计院带来了一系列的问题。好在浙江省电力设计院带及时使用了朝天椒USB Server方案,实现了加密狗的集中安全管控,避免了加密狗因为管理不善和遗失可能带来的巨…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

【android bluetooth 框架分析 04】【bt-framework 层详解 1】【BluetoothProperties介绍】
1. BluetoothProperties介绍 libsysprop/srcs/android/sysprop/BluetoothProperties.sysprop BluetoothProperties.sysprop 是 Android AOSP 中的一种 系统属性定义文件(System Property Definition File),用于声明和管理 Bluetooth 模块相…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

Android Bitmap治理全解析:从加载优化到泄漏防控的全生命周期管理
引言 Bitmap(位图)是Android应用内存占用的“头号杀手”。一张1080P(1920x1080)的图片以ARGB_8888格式加载时,内存占用高达8MB(192010804字节)。据统计,超过60%的应用OOM崩溃与Bitm…...

laravel8+vue3.0+element-plus搭建方法
创建 laravel8 项目 composer create-project --prefer-dist laravel/laravel laravel8 8.* 安装 laravel/ui composer require laravel/ui 修改 package.json 文件 "devDependencies": {"vue/compiler-sfc": "^3.0.7","axios": …...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

SiFli 52把Imagie图片,Font字体资源放在指定位置,编译成指定img.bin和font.bin的问题
分区配置 (ptab.json) img 属性介绍: img 属性指定分区存放的 image 名称,指定的 image 名称必须是当前工程生成的 binary 。 如果 binary 有多个文件,则以 proj_name:binary_name 格式指定文件名, proj_name 为工程 名&…...

CSS | transition 和 transform的用处和区别
省流总结: transform用于变换/变形,transition是动画控制器 transform 用来对元素进行变形,常见的操作如下,它是立即生效的样式变形属性。 旋转 rotate(角度deg)、平移 translateX(像素px)、缩放 scale(倍数)、倾斜 skewX(角度…...

【Android】Android 开发 ADB 常用指令
查看当前连接的设备 adb devices 连接设备 adb connect 设备IP 断开已连接的设备 adb disconnect 设备IP 安装应用 adb install 安装包的路径 卸载应用 adb uninstall 应用包名 查看已安装的应用包名 adb shell pm list packages 查看已安装的第三方应用包名 adb shell pm list…...

WebRTC从入门到实践 - 零基础教程
WebRTC从入门到实践 - 零基础教程 目录 WebRTC简介 基础概念 工作原理 开发环境搭建 基础实践 三个实战案例 常见问题解答 1. WebRTC简介 1.1 什么是WebRTC? WebRTC(Web Real-Time Communication)是一个支持网页浏览器进行实时语音…...
