C++函数内联详解
本文旨在讲解C++中的函数内联相关知识,读完这篇文章,希望读者们会对函数内联有更深一步的认识!
内联函数的定义
在计算机科学中, 内联函数 (有时称作 在线函数 或 编译时期展开函数 )是一种编程语言结构,用来建议 编译器 对一些特殊 函数 进行内联扩展(有时称作在线扩展 ;也就是说建议编译器将指定的函数体插入并取代每一处调用该函数的地方( 上下文 ),从而节省了每次调用函数带来的额外时间开支)
C++引进内联函数的原因
C++语言支持内联函数,其目的是为了提高函数的执行效率(速度)。
宏定义的缺陷
在C程序中,常常使用宏定义来提高代码执行效率,宏定义本身不是一种函数,它只是一种简单的替代,其省去了参数压栈,生成汇编语言的CALL调用,返回参数,执行return等过程,从而提高了速度,使用宏定义的最大缺点是容易出错,预处理器在拷贝宏代码时常常会产生意想不到的边界效应!通过阅读下面代码可以发现宏定义的一些缺点!
1.代码容易出错
#define Add(x,y) x+y
int main()
{int result = 3 * Add(1, 2);cout << result << endl; //结果输入5!
}对于上述代码,初学者很容易将宏函数代码写错,没有加上括号,从而导致结果与自己预期的结果有出入!
2.宏定义不可调试
宏的另一个缺点就是不可调试,但是内联函数可以调试,内联函数不是像宏一样进行代码的展开么?怎么能够调试呢?其实内联函数的“可调试”不是说它展开后还可以调试,而是在程序的调试版本(Debug)版本里它根本没有真正的内联,编译器像普通函数那样为它生成含有调试信息的可执行代码,在程序的发行(Release)版本里,编译器才会实现真正的内联,所以我们可以通过release版本来观察其内联的实现过程!
判断函数成为内联函数

可以通过简单的调试,将代码转化为汇编代码,然后通过观察底层的实现,因为调用函数栈帧会使用Call指令,这是一种简单的观察方法!
内联函数的编程风格
注:内联函数的定义和声明不能分离!
关键字Inline必须与函数定义体放在一起才能使函数实现真正的内联,仅把inline放在函数声明的前面不起任何作用!
例如如下代码!
如下风格的Add函数不能成为内联函数!
inline void Add(int x,int y); //inline仅与函数放在声明放在一起
void Add(int x,int y)
{********
}如下风格的Add函数可以成为内联函数!void Add(int x,int y);
inline void Add(int x,int y) //inline与函数定义体放在一起!
{********
}上述不能成为内联函数的情况编译器会报出如下错误!错误如下:
 编译器不能链接Add函数,这是为什么呢?因为定义时把Add函数定义为内联类型,其作用只是单纯的展开函数,其不会在符号表调用相关字符,地址等,所以当引用Add函数时,虽然编译器认识这个函数,但是它不知道下一步该干什么(如何链接到Add函数)!
编译器不能链接Add函数,这是为什么呢?因为定义时把Add函数定义为内联类型,其作用只是单纯的展开函数,其不会在符号表调用相关字符,地址等,所以当引用Add函数时,虽然编译器认识这个函数,但是它不知道下一步该干什么(如何链接到Add函数)!
所以说,inline是一种“用于实现的关键字”,而不是一种“用于声明的关键字”,一般情况下,用户可以阅读函数声明的声明,但看不见函数的定义,尽管大多数教科书中在内联函数的声明和定义都加上了inline关键字,但是根据C++程序设计风格,inline不应出现在函数的声明中,因为用户没有必要知道函数是否需要内联!
内联函数的特性
1. inline是一种以空间换时间的做法,如果编译器将函数当成内联函数处理,在编译阶段,会用函数体替换函数调用,缺陷:可能会使目标文件变大,优势:少了调用开销,提高程序运行效率。
2. inline对于编译器而言只是一个建议,不同编译器关于inline实现机制可能不同,一般建议:将函数规模较小(即函数不是很长,具体没有准确的说法,取决于编译器内部实现)、不是递归、且频繁调用的函数采用inline修饰,否则编译器会忽略inline特性。
慎用内联函数
内联能提高函数的执行效率,为什么不把所有的函数都定义为内联函数呢?
如果所有的函数都是内联函数,还用得着“内联”这个关键字么?
内联并不是万能的!它以空间换时间为代价,仅仅省去了函数调用的开销,从而提高了程序的执行效率,注意:这里的“函数的调用开销”并不包括执行函数体所需要的开销,而是仅指参数压栈,跳转,退栈和返回操作,如果执行函数体内的代码时间比调用函数开销要大的多,那么内联的效率收入会很小,另一方面,每一处内联函数的调用都需要拷贝代码,使得程序的总代码量增大,消耗更多的内存空间!
以下情况不宜使用内联:
1.函数体内的代码较长,使用内联会使执行代码膨胀!
2.函数体内存在过多的循环或控制结构,那么执行函数体内的代码的时间会比函数调用开销大的多,因此内联的意义并不大!
至此,有关内联函数的介绍完毕,一些专业术语查自(高质量程序设计指南C/C++),希望读完这篇文章,能使读者对内联函数有更深一步的认识!

相关文章:

C++函数内联详解
本文旨在讲解C中的函数内联相关知识,读完这篇文章,希望读者们会对函数内联有更深一步的认识! 内联函数的定义 在计算机科学中, 内联函数 (有时称作 在线函数 或 编译时期展开函数 )是一种编程语言结构&…...

Revit SDK 介绍:NewForm 新建体量
前言 这个例子介绍如何新建体量。 内容 图形生成效果。 用 Extrusion 创建体量 // 创建一个轮廓 ReferenceArray ref_ar new ReferenceArray(); // 创建三条直线,并放入轮廓 Autodesk.Revit.DB.XYZ ptA new Autodesk.Revit.DB.XYZ(10, 10, 0); Autodesk.Rev…...

Ubuntu离线或在线安装Python解释器
这里以安装Python3.5.7为例。 首先进入官网,下载Python-3.5.7.tgz,或者使用以下命令下载(需要联网): wget https://www.python.org/ftp/python/3.5.7/Python-3.5.7.tgz下载完成后,使用以下命令进行解压缩…...

微信小程序隐私协议相关接口实际使用方式
<view wx:if"{{showPrivacy}}" class"privacy"><view class"popup"><view>隐私弹窗内容....</view><view bindtap"openPrivacyAgreement">点击查看隐私协议</view><button id"disagreeBt…...

MySQL--MySQL表的增删改查(进阶)
check 聚合查找 count sum average max min 我们这里先构造出多张表 查询lisi同学的成绩 来自student和来自score c 增加名字这一条件 查询所有同学的总成绩以及个人信息 来自score和来自student 查询所有同学的各科成绩以及个人信息 来自student,course和…...

Golang 中的静态类型和动态类型
定义说明 静态类型(static type):在编码时就能确定的类型,通过变量定义可以确定的类型;动态类型(concrete type):在运行时才能确定具体的数据类型; 动态静态类型如何理…...

docker的数据卷、docker数据持久化
目录 前言docker数据持久化的2种方式数据卷 bind mount ,即-v参数匿名数据卷 docker manager volume-v参数和匿名卷的区别docker volume 命令的使用数据卷容器孤儿volume总结 前言 环境:centos7.9 docker version 20.10.14 本篇我们来介绍docker的数据卷…...
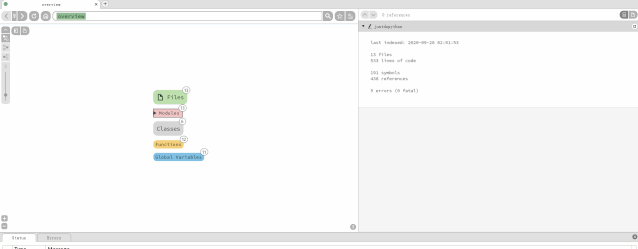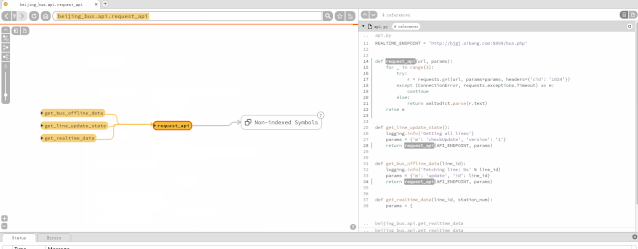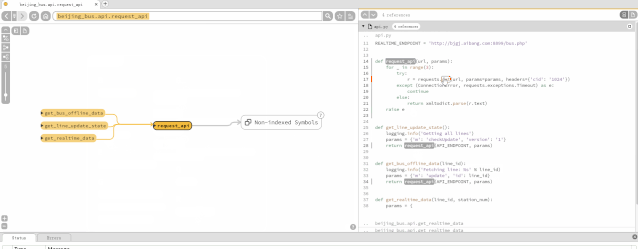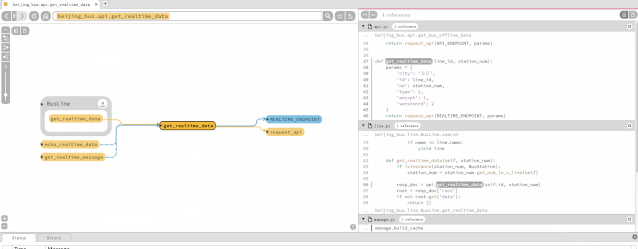
阅读源码工具Sourcetrail
收费工具Source Insight、Understand Sourcetrail开源工具 一、下载安装 接下来就是download,在GitHub的release页面选择自己系统对应的发布版本下载安装: 安装好后,运行程序,会出现这样的界面: 二、应用 选择“New…...

KMP 算法详解
KMP算法详解 1 KMP算法解决的问题 2 前缀问题 3 KMP 算法 1 KMP算法解决的问题 字符串str1和str2,str1是否包含str2,如果包含返回str2在str1中开始的位置。并做到时间复杂度为 O ( n ) O(n) O(n) 2 前缀问题 求一个字符串中每个字符前缀和后缀相…...

[matconvnet]matconvnet-1.0-beta-25在cuda11.1以上编译问题总结
首先可以肯定是matconvnet-1.0-beta-25不支持cuda11.1及其以上版本,因为cudnn版本问题导致源码api接口不一样,会下面类似报错 E:\Matlab\R2020a\matconvnet-1.0-beta25\matlab\src\bits\datacu.hpp(89): error: identifier "cudnnConvolutionFwdPr…...

自动化驱动程序管理
在部署操作系统时,每次都从下载和分发所需的驱动程序中实现真正的独立性可能是一场艰苦的战斗。特别是具有硬件多样化的环境,并且需要支持新的硬件类型时。借助 OS Deployer,可以对所有端点使用一个映像,无论品牌和型号如何&#…...
区块哈希介绍)
智能合约编写高级篇(二)区块哈希介绍
本文档从区块哈希基本概念出发,详细介绍了中移链的区块哈希交易接口和应用方向。适用于EOS区块链智能合约高级开发人员,熟悉如何获取当前发生交易所在的区块号和区块哈希前缀,并通过Tapos机制验证交易的有效性。 01 概述 (一&…...
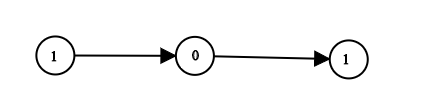
二进制链表转整数
给你一个单链表的引用结点 head。链表中每个结点的值不是 0 就是 1。已知此链表是一个整数数字的二进制表示形式。 请你返回该链表所表示数字的 十进制值 。 示例 1: 输入:head [1,0,1] 输出:5 解释:二进制数 (101) 转化为十进…...

Python爬虫进阶:使用Scrapy库进行数据提取和处理
在我们的初级教程中,我们介绍了如何使用Scrapy创建和运行一个简单的爬虫。在这篇文章中,我们将深入了解Scrapy的强大功能,学习如何使用Scrapy提取和处理数据。 一、数据提取:Selectors和Item 在Scrapy中,提取数据主要…...

五)Stable Diffussion使用教程:文生图之高清修复
上一篇我们说到图生图,这一篇来说说高清修复。 上一篇我们通过一个例子实现了图生图的功能,使用一张图片生成了另一种风格的图片。 然而,我们生成的图片质量不尽如人意。 虽然我们之前也提到设置分辨率、精炼提示词去提升画面质量等等,但是实际用下来发现,分辨率拉得太…...

SQL SERVER 如何实现UNDO REDO 和PostgreSQL 有近亲关系吗
开头还是介绍一下群,如果感兴趣PolarDB ,MongoDB ,MySQL ,PostgreSQL ,SQL Server,Redis ,Oracle ,Oceanbase 等有问题,有需求都可以加群群内有各大数据库行业大咖,CTO,可以解决你的问题。加群请加微信号 l…...
SpringBoot原理-自动配置-原理分析-源码跟踪
自动配置原理 SpringBootApplication 该注解标识在SpringBoot项目的启动类上,是SpringBoot中最为重要的注解,该注解由三个部分组成。 SpringBootConfiguration:该注解与Configuration注解作用一样,用来声明当前类为一个配置类Comp…...

安全基础 --- 原型链污染
原型链 大部分面向对象的编程语言,都是通过“类”(class)实现对象的继承。传统上,JavaScript 语言的继承不通过 class,而是通过“原型对象”(prototype)实现 1、prototype 属性的作用 JavaScri…...

c++中的常用知识点总结
命名空间 使用命名空间之后,调用代码时可以省去也可以不省去相关的前缀。 #include <iostream>using namespace std;//使用c自己的命名空间 int main() {int num1 10;std::cout << "Hello, World!" << std::endl;cout<<num1&l…...

Leetcode:349. 两个数组的交集【题解超详细】
题目 给定两个数组 nums1 和 nums2 ,返回 它们的交集 。输出结果中的每个元素一定是 唯一 的。我们可以 不考虑输出结果的顺序 。 难度:简单 题目链接:349.两个数组的交集 示例 1: 输入:nums1 [1,2,2,1], nums2 [2,…...

KubeSphere 容器平台高可用:环境搭建与可视化操作指南
Linux_k8s篇 欢迎来到Linux的世界,看笔记好好学多敲多打,每个人都是大神! 题目:KubeSphere 容器平台高可用:环境搭建与可视化操作指南 版本号: 1.0,0 作者: 老王要学习 日期: 2025.06.05 适用环境: Ubuntu22 文档说…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...

【Zephyr 系列 10】实战项目:打造一个蓝牙传感器终端 + 网关系统(完整架构与全栈实现)
🧠关键词:Zephyr、BLE、终端、网关、广播、连接、传感器、数据采集、低功耗、系统集成 📌目标读者:希望基于 Zephyr 构建 BLE 系统架构、实现终端与网关协作、具备产品交付能力的开发者 📊篇幅字数:约 5200 字 ✨ 项目总览 在物联网实际项目中,**“终端 + 网关”**是…...

工业自动化时代的精准装配革新:迁移科技3D视觉系统如何重塑机器人定位装配
AI3D视觉的工业赋能者 迁移科技成立于2017年,作为行业领先的3D工业相机及视觉系统供应商,累计完成数亿元融资。其核心技术覆盖硬件设计、算法优化及软件集成,通过稳定、易用、高回报的AI3D视觉系统,为汽车、新能源、金属制造等行…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

html-<abbr> 缩写或首字母缩略词
定义与作用 <abbr> 标签用于表示缩写或首字母缩略词,它可以帮助用户更好地理解缩写的含义,尤其是对于那些不熟悉该缩写的用户。 title 属性的内容提供了缩写的详细说明。当用户将鼠标悬停在缩写上时,会显示一个提示框。 示例&#x…...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...
