动态规划之子数组系列
子数组系列
- 1. 环形⼦数组的最⼤和
- 2. 乘积最大子数组
- 3. 等差数列划分
- 4. 最长湍流子数组
- 5. 单词拆分
- 6. 环绕字符串中唯⼀的子字符串
1. 环形⼦数组的最⼤和
1.题目链接:环形⼦数组的最⼤和
2.题目描述:给定一个长度为 n 的环形整数数组 nums ,返回 nums 的非空 子数组 的最大可能和 。
环形数组 意味着数组的末端将会与开头相连呈环状。形式上, nums[i] 的下一个元素是 nums[(i + 1) % n] , nums[i] 的前一个元素是 nums[(i - 1 + n) % n] 。
子数组 最多只能包含固定缓冲区 nums 中的每个元素一次。形式上,对于子数组 nums[i], nums[i + 1], …, nums[j] ,不存在 i <= k1, k2 <= j 其中 k1 % n == k2 % n 。
示例 1:
输入:nums = [1,-2,3,-2]
输出:3
解释:从子数组 [3] 得到最大和 3
示例 2:
输入:nums = [5,-3,5]
输出:10
解释:从子数组 [5,5] 得到最大和 5 + 5 = 10
示例 3:
输入:nums = [3,-2,2,-3]
输出:3
解释:从子数组 [3] 和 [3,-2,2] 都可以得到最大和 3
提示:
n == nums.length
1 <= n <= 3 * 10^4
-3 * 10^4 <= nums[i] <= 3 * 10^4
3.问题分析:这道题对于一个数组来说,逻辑上首尾是相连的,求子数组的最大和;直接求肯定是求不出来的,还记得清上篇多状态中有道打家劫舍II也是对于环形数组求解,那道题中一个房子如果偷的话,那么相邻的房子就不能再偷,我们对首尾进行详细分析,对[0, n - 2]和[1, n - 1]区间分别进行操作;这道题和那道题没关系哈,提出来只是让大家回忆一下,接下来就是这道题的思路;说难也不难,但是确实不好太想到,首先会有两种结果1. 结果在数组的内部,包括整个数组;2. 结果在数组⾸尾相连的⼀部分上。整个数组的总和sum是不变的,如果结果在数组⾸尾相连的⼀部分上,那么数组中间就会空出来一部分选不上,中间没选上的数组和就是子数组和的最小值;所以这道题求一个最大子数组和与一个最小子数组和,然后用sum减去最小子数组和与所求最大子数组和作比较,返回最大的那一个即可。
- 状态表示:f[i] 表⽰:以 i 做结尾的所有⼦数组中和的最大值;g[i] 表⽰:以 i 做结尾的所有⼦数组中和的最⼩值。
- 状态转移方程:f[i] 的所有可能可以分为以下两种:1.⼦数组的⻓度为 1 :此时 f[i] = nums[i] ;2.⼦数组的⻓度⼤于 1 :此时 f[i] 应该等于 以 i - 1 做结尾的所有⼦数组中和的最⼤值再加上 nums[i] ,也就是 f[i - 1] + nums[i] 。由于要的是最⼤值,因此应该是两种情况下的最⼤值,因此可得转移⽅程:
f[i] = max(nums[i], f[i - 1] + nums[i]);g[i]的分析与f[i]基本相同,可得g[i]的状态转移方程为g[i] = min(nums[i], g[i - 1] + nums[i])。 - 初始化:要求f[i],那么就需要知道f[i - 1]的值,所以只需要处理i - 1越界这种情况,通常增加一个辅助结点即可,增加辅助结点后要记得nums[i - 1]要减1 ;初始化为 f[0] = g[0] = 0 。
- 填表顺序:从左往右。
- 返回值:找出f[i]中最大,g[i]中最小,用sum - min(g[i]),返回减去的值和f[i]中的最大值。有个特殊情况,就是当相减的数为0(即数组中的数全为负数),此时应该返回f[i]中的最大值,否则就返回减去的值和f[i]中的最大值。
4.代码如下:
class Solution
{
public:int maxSubarraySumCircular(vector<int>& nums) {int n = nums.size();vector<int> f(n + 1), g(n + 1);int sum = 0;int fmax = INT_MIN; //f数组中的最大值int gmin = INT_MAX; //g数组中的最小值for (int i = 1; i <= n; ++i){f[i] = max(f[i - 1] + nums[i - 1], nums[i - 1]);fmax = max(fmax, f[i]);g[i] = min(g[i - 1] + nums[i - 1], nums[i - 1]);gmin = min(gmin, g[i]);sum += nums[i - 1];}gmin = sum - gmin;return gmin == 0 ? fmax : max(fmax, gmin);}
};
2. 乘积最大子数组
1.题目链接:添加链接描述
2.题目描述:给你一个整数数组 nums ,请你找出数组中乘积最大的非空连续子数组(该子数组中至少包含一个数字),并返回该子数组所对应的乘积。
测试用例的答案是一个 32位 整数。
子数组 是数组的连续子序列。
示例 1:
输入: nums = [2,3,-2,4]
输出: 6
解释: 子数组 [2,3] 有最大乘积 6。
示例 2:
输入: nums = [-2,0,-1]
输出: 0
解释: 结果不能为 2, 因为 [-2,-1] 不是子数组。
提示:
1 <= nums.length <= 2 * 10^4
-10 <= nums[i] <= 10
nums 的任何前缀或后缀的乘积都 保证 是一个 32-位 整数
3.问题分析:如果用一个dp表来表示乘积最大的子数组,就会发现当出现负数时一个dp表是不能表示出来的,负数乘负数可能会是最大的乘积。所以可以用两个dp表来表示,一个表为f:表示前i个元素,子数组乘积的最大值;另一个表为g:表示前i个元素中,子数组乘积的最小值。
- 状态表示:如上所述,f表:表示前i个元素,子数组乘积的最大值;g表:表示前i个元素中,子数组乘积的最小值。
- 状态转移方程:对于 f[i] ,也就是「以 i 为结尾的所有⼦数组的最⼤乘积」,对于所有⼦数组,可以分为下⾯三种形式:
1.⼦数组的⻓度为 1 ,也就是 nums[i] ;2.⼦数组的⻓度⼤于 1 ,但 nums[i] > 0 ,此时需要的是 i - 1 为结尾的所有⼦数组的最⼤乘积 f[i - 1] ,再乘上 nums[i] ,也就是 nums[i] * f[i - 1] ;3.⼦数组的⻓度⼤于 1 ,但 nums[i] < 0 ,此时需要的是 i - 1 为结尾的所有⼦数组的最⼩乘积 g[i - 1] ,再乘上 nums[i] ,也就是 nums[i] * g[i - 1] ;综上所述, f[i] = max(nums[i], max(nums[i] * f[i - 1], nums[i] * g[i - 1]) )。
对于 g[i] ,也就是以 i 为结尾的所有⼦数组的最⼩乘积,分析结果如同f[i]。 - 初始化:要求 i 结尾的需要知道i - 1位置的值,所以可以增加一个辅助结点,求的是乘积的结果,所以f[0] = 1; g[0] = 1。
- 填表顺序:从左往右。
- 返回值:返回f表中最大的元素。
4.代码如下:
class Solution
{
public:int maxProduct(vector<int>& nums) {int n = nums.size();vector<int> f(n + 1), g(n + 1);f[0] = g[0] = 1;int ret = INT_MIN;for (int i = 1; i <= n; ++i){int x = nums[i - 1], y = f[i - 1] * nums[i - 1], z = g[i - 1] * nums[i - 1];f[i] = max(x, max(y, z));g[i] = min(x, min(y, z));ret = max(ret, f[i]);}return ret;}
};
3. 等差数列划分
1.题目链接:等差数列划分
2.题目描述:
如果一个数列 至少有三个元素 ,并且任意两个相邻元素之差相同,则称该数列为等差数列。
例如,[1,3,5,7,9]、[7,7,7,7] 和 [3,-1,-5,-9] 都是等差数列。
给你一个整数数组 nums ,返回数组 nums 中所有为等差数组的 子数组个数。
子数组 是数组中的一个连续序列。

3.算法流程:
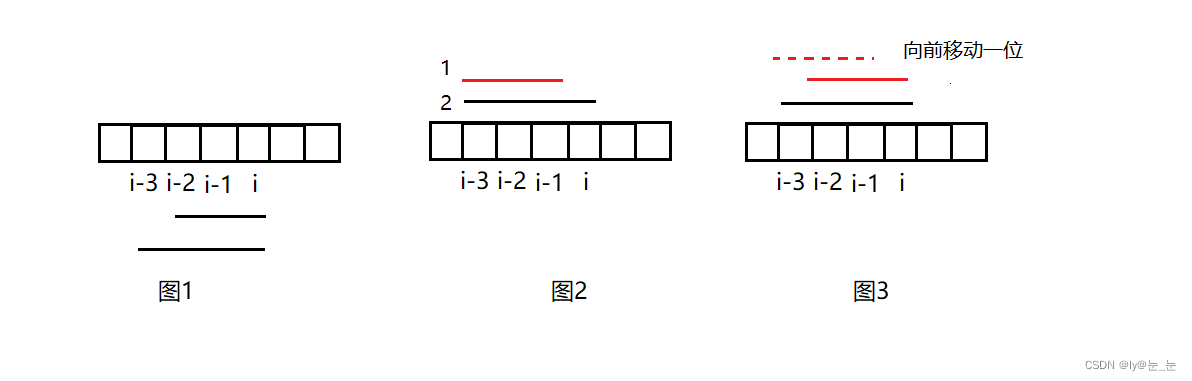
- 状态表示
这道题以某一个位置为结尾进行分析(如图1),dp[i] 表示以 i 位置的元素为结尾的等差数列有多少种。 - 状态转移方程
1.如图2,假设上述4个位置构成等差数列,红线1表示以i-1为结尾的等差数列的数量;将红线1向后移动一格,那么这条红线是不是就可以代表以i为结尾的等差数列,但是刚好少了黑线2这种情况,所以以i为结尾的等差数列个数等于(红线1)以i-1为结尾的等差数列个数+1(黑线2这种多出来的情况),即dp[i] = dp[i - 1] + 1(如果是等差数列的话)。
2.如果以i为结尾的元素不构成等差数列,那么这个位置的dp[i]=0,因为dp表示以i位置的元素为结尾的等差数列的个数。
之后将以所有元素为结尾的等差数列加起来即为所求。 - 初始化
前两个位置的元素⽆法构成等差数列,因此 dp[0] = dp[1] = 0 。 - 填表顺序:从左往右。
- 返回值:要求的是所有的等差数列的个数,因此需要返回整个 dp 表⾥⾯的元素之和。
4.代码如下:
class Solution
{
public:int numberOfArithmeticSlices(vector<int>& nums) {int n = nums.size();vector<int> dp(n);int ret = 0;for (int i = 2; i < n; ++i){if ((nums[i] - nums[i-1]) == (nums[i-1] - nums[i-2]))dp[i] = dp[i-1] + 1;ret += dp[i];}return ret;}
};
4. 最长湍流子数组
1.题目链接:最长湍流子数组
2.题目描述:给定一个整数数组 arr ,返回 arr 的 最大湍流子数组的长度 。
如果比较符号在子数组中的每个相邻元素对之间翻转,则该子数组是 湍流子数组 。
更正式地来说,当 arr 的子数组 A[i], A[i+1], …, A[j] 满足仅满足下列条件时,我们称其为湍流子数组:
若 i <= k < j :当 k 为奇数时, A[k] > A[k+1],且当 k 为偶数时,A[k] < A[k+1];
或 若 i <= k < j :当 k 为偶数时,A[k] > A[k+1] ,且当 k 为奇数时, A[k] < A[k+1]。
示例 1:
输入:arr = [9,4,2,10,7,8,8,1,9]
输出:5
解释:arr[1] > arr[2] < arr[3] > arr[4] < arr[5]
示例 2:
输入:arr = [4,8,12,16]
输出:2
示例 3:
输入:arr = [100]
输出:1
3.问题分析:这道题需要找最长交错的子数组,交错就是 i 位置的比 i - 1 的值要大(小),i + 1位置的比 i 位置要小(大),可以说要求交错的最长子数组。首先想用一个dp表来解决,会发现数组中的值一会比前一个大,一会又比前一个小,用一个dp表表示不了,再用两个dp表来试试,数组中的元素一会大一会小,那么就用f[i]来表示 i 位置的元素比 i - 1 中的元素大,所存的最长子数组;用g[i]来表示 i 位置的元素比 i - 1 中的元素小,所存的最长子数组,这样表示这道题就会很容易求出来。
- 状态表示:
f[i]来表示 i 位置的元素比 i - 1 中的元素大,所存的最长子数组;用g[i]来表示 i 位置的元素比 i - 1 中的元素小,所存的最长子数组。 - 状态转移方程:1.arr[i] > arr[i - 1] :如果 i 位置的元素⽐ i - 1 位置的元素⼤,说明接下来应该去找 i -1 位置结尾,并且 i - 1 位置元素⽐前⼀个元素⼩的序列,那就是 g[i - 1] 。更新 f[i] 位置的值:
f[i] = g[i - 1] + 1; 2.arr[i] < arr[i - 1] :如果 i 位置的元素⽐ i - 1 位置的元素⼩,说明接下来应该去找 i - 1 位置结尾,并且 i - 1 位置元素⽐前⼀个元素⼤的序列,那就是f[i - 1] 。更新 g[i] 位置的值:g[i] = f[i - 1] + 1; arr[i] == arr[i - 1] :不构成湍流数组。 - 初始化:两个dp表中所有的值可以初始化为1.因为最短的长度为1;然后从 i = 1开始遍历,i - 1>= 0,dp表是不会越界的,所以这道题就不用增加辅助结点。
- 填表顺序:从左往右,依次填写。
- 返回值:返回两个dp表中的最大值。
4.代码如下:
class Solution
{
public:int maxTurbulenceSize(vector<int>& arr) {int n = arr.size();vector<int> f(n, 1), g(n, 1);int ret = 1;for (int i = 1; i < n; ++i){if (arr[i] > arr[i - 1])f[i] = g[i - 1] + 1;else if (arr[i] < arr[i - 1])g[i] = f[i - 1] + 1;ret = max(ret, max(f[i], g[i]));}return ret;}
};
5. 单词拆分
1.题目链接:单词拆分
2.题目描述:给你一个字符串 s 和一个字符串列表 wordDict 作为字典。请你判断是否可以利用字典中出现的单词拼接出 s 。
注意:不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。
示例 1:
输入: s = “leetcode”, wordDict = [“leet”, “code”]
输出: true 解释: 返回 true
因为 “leetcode” 可以由 “leet” 和 “code” 拼接成。
示例 2:
输入: s = “applepenapple”, wordDict = [“apple”, “pen”] 输出: true 解释: 返回
true 因为 “applepenapple” 可以由 “apple” “pen” “apple” 拼接成。
注意,你可以重复使用字典中的单词。
示例 3:
输入: s = “catsandog”, wordDict = [“cats”, “dog”, “sand”, “and”, “cat”]
输出: false
提示:
1 <= s.length <= 300
1 <= wordDict.length <= 1000
1 <= wordDict[i].length <= 20 s 和 wordDict[i] 仅由小写英文字母组成 wordDict 中的所有字符串互不相同
3.问题分析:要利用字典中出现的单词拼接出 s ,那么就可以认为从s中的0位置拿一个子数组与字典中的元素匹配,然后再向后拿一个子数组匹配,如果s中的每个子数组都可以在字典中找到,那么可以利用字典中出现的单词拼接出 s 。
- 状态标识:dp[i] 表⽰: [0, i] 区间内的字符串,能否被字典中的单词拼接⽽成。
- 状态转移方程:对于 dp[i] ,为了确定当前的字符串能否由字典⾥⾯的单词构成,根据最后⼀个单词的起始位置 j ,可以将其分解为前后两部分: 前⾯⼀部分 [0, j - 1] 区间的字符串; 后⾯⼀部分 [j, i] 区间的字符串。其中前⾯部分我们可以在 dp[j - 1] 中找到答案,后⾯部分的⼦串可以在字典⾥⾯找到。因此, 当dp[j - 1] = true,并且后⾯部分的⼦串 s.substr(j, i - j + 1) 能够在字典中找到,那么 dp[i] = true 。
- 初始化:增加一个辅助结点,dp[0]表示0个字符能否被拼接而成,0个字符串也就是空串,所以dp[0] = true,因为增加了一个辅助结点,所以遍历s是要减1 。
- 填表顺序:从左往右
- 返回值:返回 dp[n] 位置的布尔值。
4.代码如下:
class Solution
{
public:bool wordBreak(string s, vector<string>& wordDict){//将字典⾥⾯的单词存在哈希表⾥⾯unordered_set<string> hash;for (auto& s : wordDict) hash.insert(s);int n = s.size();vector<bool> dp(n + 1);dp[0] = true; // 保证后续填表是正确的for (int i = 1; i <= n; i++) // 填 dp[i]{for (int j = i; j >= 1; j--) //最后⼀个单词的起始位置{if (dp[j - 1] && hash.count(s.substr(j - 1, i - j + 1))) //添加辅助结点,对应的位置为j - 1{dp[i] = true;break;}}}return dp[n];}
};
6. 环绕字符串中唯⼀的子字符串
1.题目链接:环绕字符串中唯⼀的子字符串
2.问题描述:
定义字符串 base 为一个 “abcdefghijklmnopqrstuvwxyz” 无限环绕的字符串,所以 base 看起来是这样的:
“…zabcdefghijklmnopqrstuvwxyzabcdefghijklmnopqrstuvwxyzabcd…”.
给你一个字符串 s ,请你统计并返回 s 中有多少 不同非空子串 也在 base 中出现。
示例 1:
输入:s = “a”
输出:1
解释:字符串 s 的子字符串 “a” 在 base 中出现。
示例 2:
输入:s = “cac”
输出:2
解释:字符串 s 有两个子字符串 (“a”, “c”) 在 base 中出现。
示例 3:
输入:s = “zab”
输出:6
解释:字符串 s 有六个子字符串 (“z”, “a”, “b”, “za”, “ab”, and “zab”) 在 base 中出现。
提示:
1 <= s.length <= 10^5
s 由小写英文字母组成
3.问题分析:这道题其实可以说寻找递增子数组的个数,比如如果只有a到y,(并且元素不重复)用一个dp表,i 位置表示的是以 i 结尾子数组的个数,将每块相连的递增子数组个数相加即将dp表中的元素求和;现在再加一个z,并且z到a可以看作是连接的,那么就加个if语句将这种情况判断一下即可;然后再加一个条件元素可以重复,但是题中所求子数组是不能重复,dp表是的是以i为结尾子数组的个数,比如aababc(“a”,“b”,“c”,“ab”,“bc”,“abc”),对于后面的abc来说已经包含前面的ab了,所以只用求出以某个结尾的最大子数组的个数,用一个哈希数组可以来解决,如果s[i]的元素一样,那么就保留dp[i]中的最大值。
- 状态表示:dp[i] 表⽰:以 i 位置的元素为结尾的所有⼦串⾥⾯,有多少个在 base 中出现过。
- 状态转移方程:就是寻找递增子数组的个数,如等差数列划分,
即dp[i] = dp[i - 1] + 1(如果是等差数列的话)。 - 初始化:这道题的长度可以为1,而等差序列划分最少要为3,所以将dp表都初始化为1.
- 填表顺序:从左往右。
- 返回值:返回哈希数组中元素的和。
代码如下:
class Solution
{
public:int findSubstringInWraproundString(string s){int n = s.size();// 1. 利⽤ dp 求出每个位置结尾的最⻓连续⼦数组的⻓度vector<int> dp(n, 1);for (int i = 1; i < n; i++)if (s[i] - 1 == s[i - 1] || (s[i - 1] == 'z' && s[i] == 'a'))dp[i] = dp[i - 1] + 1;// 2. 计算每⼀个字符结尾的最⻓连续⼦数组的⻓度int hash[26] = { 0 };for (int i = 0; i < n; i++)hash[s[i] - 'a'] = max(hash[s[i] - 'a'], dp[i]);// 3. 将结果累加起来int sum = 0;for (auto x : hash) sum += x;return sum;}
};
相关文章:

动态规划之子数组系列
子数组系列 1. 环形⼦数组的最⼤和2. 乘积最大子数组3. 等差数列划分4. 最长湍流子数组5. 单词拆分6. 环绕字符串中唯⼀的子字符串 1. 环形⼦数组的最⼤和 1.题目链接:环形⼦数组的最⼤和 2.题目描述:给定一个长度为 n 的环形整数数组 nums ,…...
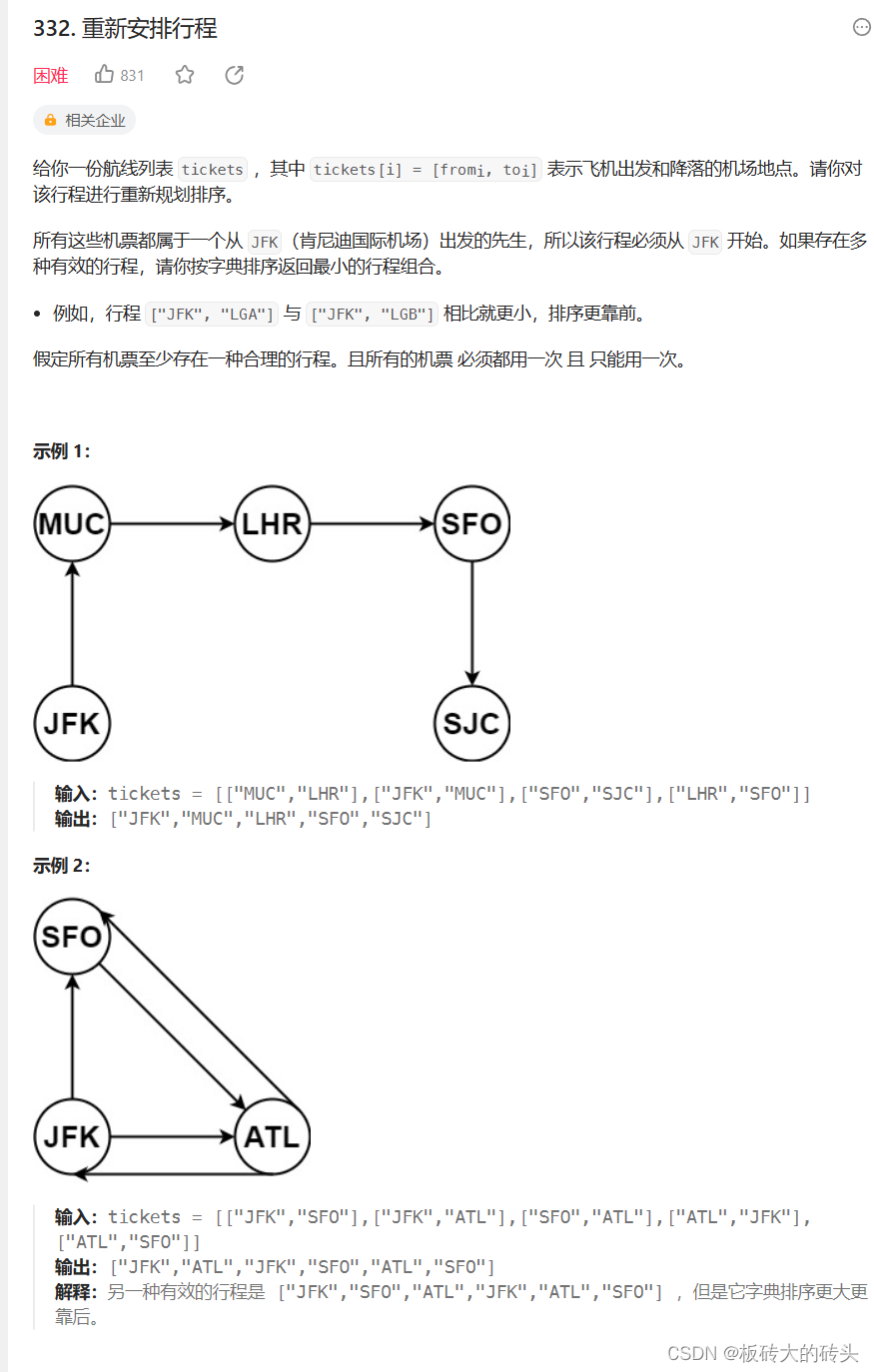
LeetCode(力扣)332.重新安排行程Python
LeetCode332.重新安排行程 题目链接代码 题目链接 https://leetcode.cn/problems/reconstruct-itinerary/ 代码 class Solution:def backtracking(self, tickets, used, cur, result, path):if len(path) len(tickets) 1:result.append(path[:])return Truefor i, ticket…...
的问题))
Pytho 从列表中创建字典 (dict.fromkeys()的问题)
问题起因:想在代码中通过已有的列表创建一个字典,但是又不想写循环,更不想手动填,所以用到了字典对象的fromkeys()方法 。 先以一个简单的例子介绍一下该方法: a ["A", "B", "C", &qu…...

第14节-PhotoShop基础课程-图框工具
文章目录 前言1.矩形画框2.椭圆画框 前言 图框 上面两张图,生成下面一幅图,这个就是图框工具的作用 图框工具ICON 1.矩形画框 2.椭圆画框...

使用 Nacos 在 Spring Boot 项目中实现服务注册与配置管理
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🦄 博客首页——🐅🐾猫头虎的博客🎐 🐳 《面试题大全专栏》 🦕 文章图文…...

package.json中workspaces详解与monorepo
参考package.json配置详解,让你一看就会(下) - 掘金...

Spring Boot + Vue的网上商城之商品信息展示
Spring Boot Vue的网上商城之商品信息展示 当实现一个Spring Boot Vue的网上商城的商品信息展示时,可以按照以下步骤进行: 后端实现: 创建一个Spring Boot项目,并添加所需的依赖,包括Spring Web和Spring Data JPA。…...
深度优先搜索遍历与广度优先搜索遍历
目录 一.深度优先搜索遍历 1.深度优先遍历的方法 2.采用邻接矩阵表示图的深度优先搜索遍历 3.非连通图的遍历 二.广度优先搜索遍历 1.广度优先搜索遍历的方法 2.非连通图的广度遍历 3.广度优先搜索遍历的实现 4.按广度优先非递归遍历连通图 一.深度优先搜索遍历 1.深…...

java 中 返回一个空Map
原文链接:Map用法总结 Constructs an empty HashMap with the default initial capacity (16) (mutable) // Constructs an empty HashMap with the default initial capacity (16) and the default load fact // Since:1.2 Map<String, …...

sql 执行插入多条语句中 n个insert 与 一个insert+多个values 性能上有和区别 -- chatGPT
在 SQL 中,你可以使用多种方式来插入多条记录。其中两种常见的方式是: 1. **多个 INSERT 语句**:每个 INSERT 语句都插入一行记录。 sql INSERT INTO table_name (column1, column2, ...) VALUES (value1_1, value1_2, ...); INSERT INTO …...

数学建模国赛C蔬菜类商品的自动定价与补货决策C
数学建模国赛C蔬菜类商品的自动定价与补货决策C 完整思路和代码请私信~~~ 1.拟解决问题 这是一个关于生鲜商超蔬菜商品管理的复杂问题,需要综合考虑销售、补货、定价等多个方面。以下是对这些问题的总结: 问题 1: 蔬菜销售分析 需要分析蔬菜各品类和…...
的重要性)
在程序开发中,接口(interface)的重要性
开了很多人写的程序,都适用了接口,也适用了注入,也没有感到什么不妥。如果只是为了注入而写接口,其实我感觉大可不必,特别是把接口和实体写在一个项目项目中的。 我不知道其他人怎么看接口这一层,接口最大的…...

MyBatis关联关系映射详解
前言 在使用MyBatis进行数据库操作时,关联关系映射是一个非常重要的概念。它允许我们在数据库表之间建立关联,并通过对象之间的关系来进行数据查询和操作。本文将详细介绍MyBatis中的关联关系映射,包括一对一、一对多和多对多关系的处理方法…...
常用电子元器件基础知识
目录 一、电阻 二、电容 三、电感 四、保险丝 五、二极管 一、电阻 概念:顾名思义,就是增加电流通过的阻力的。 就像是在水渠中放入东西,能阻止水的顺利通过也是一个道理。 基于电阻的电气特性,电阻在电路中主要有以下四个…...
git撤销还未push的的提交
怎样撤销掉上图中的提交呢 使用以下代码即可提交 git reset --soft HEAD^...

MySQL--数据库基础
数据库分类 数据库大体可以分为 关系型数据库 和 非关系型数据库 常用数据类型 数值类型: 分为整型和浮点型: 字符串类型 日期类型...
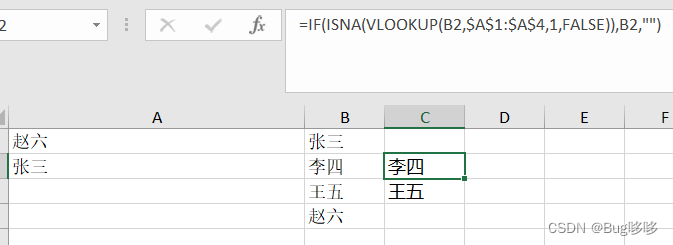
Excel相关笔记
1、找出B列中A列没有的数据并放在C列 公式:IF(ISNA(VLOOKUP(B1,$A 1 : 1: 1:A$4,1,FALSE)),B1,“”)...
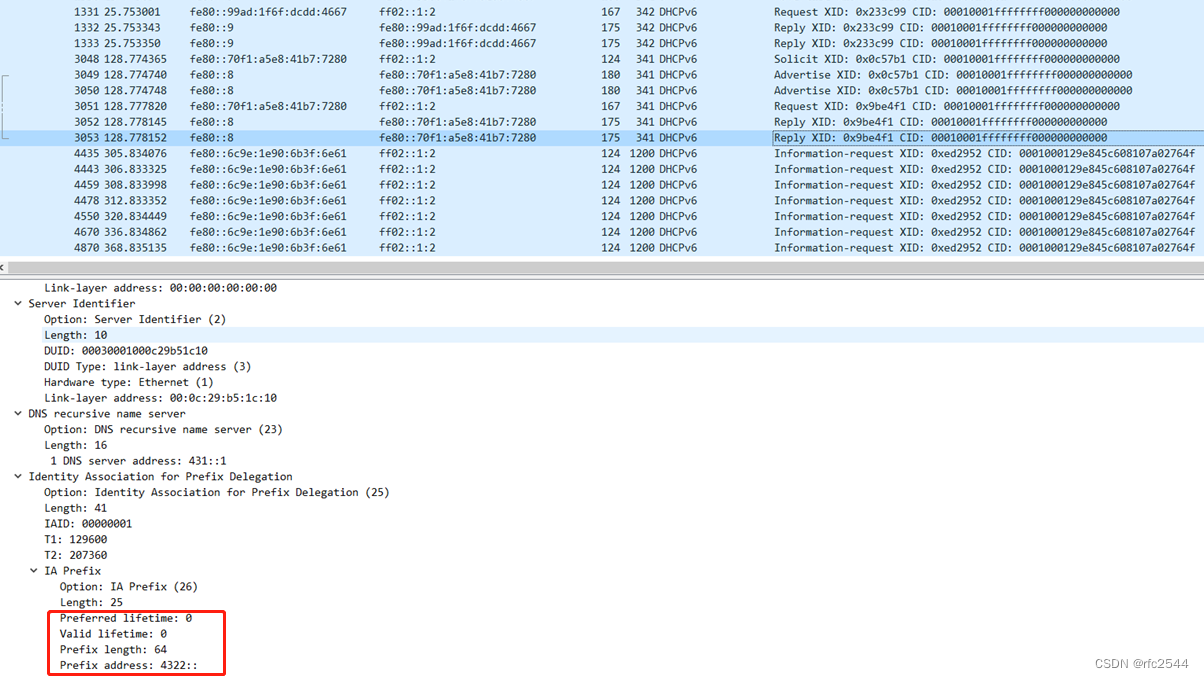
RouterOS-配置PPPoEv4v6 Server
1 接口 ether3 出接口 ether4 内网接口 2 出接口 出接口采用PPPoE拨号SLAAC获取前缀,手动配置后缀 2.1 选择出接口interface,配置PPPoE client模式 2.2 配置PPPoE client用户名和密码 2.3 从PPPoE client获取前缀地址池 2.4 给出接口选择前缀并配置…...

PhpStorm软件安装包分享(附安装教程)
目录 一、软件简介 二、软件下载 一、软件简介 PhpStorm是一款由JetBrains开发的专业PHP集成开发环境(IDE),旨在提供全面的PHP开发支持。它是基于IntelliJ IDEA平台构建的,具有强大的功能和工具,可以帮助开发人员提高…...

JavaScript设计模式(三)——单例模式、装饰器模式、适配器模式
个人简介 👀个人主页: 前端杂货铺 🙋♂️学习方向: 主攻前端方向,正逐渐往全干发展 📃个人状态: 研发工程师,现效力于中国工业软件事业 🚀人生格言: 积跬步…...

wordpress后台更新后 前端没变化的解决方法
使用siteground主机的wordpress网站,会出现更新了网站内容和修改了php模板文件、js文件、css文件、图片文件后,网站没有变化的情况。 不熟悉siteground主机的新手,遇到这个问题,就很抓狂,明明是哪都没操作错误&#x…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

CVE-2020-17519源码分析与漏洞复现(Flink 任意文件读取)
漏洞概览 漏洞名称:Apache Flink REST API 任意文件读取漏洞CVE编号:CVE-2020-17519CVSS评分:7.5影响版本:Apache Flink 1.11.0、1.11.1、1.11.2修复版本:≥ 1.11.3 或 ≥ 1.12.0漏洞类型:路径遍历&#x…...

面向无人机海岸带生态系统监测的语义分割基准数据集
描述:海岸带生态系统的监测是维护生态平衡和可持续发展的重要任务。语义分割技术在遥感影像中的应用为海岸带生态系统的精准监测提供了有效手段。然而,目前该领域仍面临一个挑战,即缺乏公开的专门面向海岸带生态系统的语义分割基准数据集。受…...

使用Spring AI和MCP协议构建图片搜索服务
目录 使用Spring AI和MCP协议构建图片搜索服务 引言 技术栈概览 项目架构设计 架构图 服务端开发 1. 创建Spring Boot项目 2. 实现图片搜索工具 3. 配置传输模式 Stdio模式(本地调用) SSE模式(远程调用) 4. 注册工具提…...

RabbitMQ入门4.1.0版本(基于java、SpringBoot操作)
RabbitMQ 一、RabbitMQ概述 RabbitMQ RabbitMQ最初由LShift和CohesiveFT于2007年开发,后来由Pivotal Software Inc.(现为VMware子公司)接管。RabbitMQ 是一个开源的消息代理和队列服务器,用 Erlang 语言编写。广泛应用于各种分布…...

【Veristand】Veristand环境安装教程-Linux RT / Windows
首先声明,此教程是针对Simulink编译模型并导入Veristand中编写的,同时需要注意的是老用户编译可能用的是Veristand Model Framework,那个是历史版本,且NI不会再维护,新版本编译支持为VeriStand Model Generation Suppo…...
