对Transformer中的Attention(注意力机制)的一点点探索
摘要:本文试图对 Transformer 中的 Attention 机制进行一点点探索。并就 6 个问题深入展开。
✅ NLP 研 1 选手的学习笔记
简介:小王,NPU,2023级,计算机技术
研究方向:文本生成、摘要生成
文章目录
- 一、为啥要写这篇博客?
- 二、一些灵魂问题,能回答上吗?
- 1. Attention 的输入是什么?输出是什么?
- 2. Attention 中的输入(input)与 “Q、K、V” 是啥关系?
- 3. Attention 中的 Q、K、V 分别有什么含义?
- 4. Attention 的计算流程是怎么样的?
- 5. 多头 Attention 有什么用?
- 6. 请介绍一下 Cross-Attention?
- 三、补充说明
一、为啥要写这篇博客?
● 调侃:因为最近在做关于 Transformer 模型的魔改,但好久没有弄这个了,已经有点记不清 Attention 的细节,今天来重温一下。借助 6 个问题来重点深入分析 Attention 机制。
● 下面这一段代码是 T5-base 的 Attention 的源码,后面我将对其进行细抠和分析。因为很多变量其实我们用不到,太冗长了,我在后面贴了一段删减版的 T5Attention 代码(不影响实际效果)。
class T5Attention(nn.Module):def __init__(self, config: T5Config, has_relative_attention_bias=False):super().__init__()self.is_decoder = config.is_decoderself.has_relative_attention_bias = has_relative_attention_biasself.relative_attention_num_buckets = config.relative_attention_num_bucketsself.relative_attention_max_distance = config.relative_attention_max_distanceself.d_model = config.d_modelself.key_value_proj_dim = config.d_kvself.n_heads = config.num_headsself.dropout = config.dropout_rateself.inner_dim = self.n_heads * self.key_value_proj_dim# Mesh TensorFlow initialization to avoid scaling before softmaxself.q = nn.Linear(self.d_model, self.inner_dim, bias=False)self.k = nn.Linear(self.d_model, self.inner_dim, bias=False)self.v = nn.Linear(self.d_model, self.inner_dim, bias=False)self.o = nn.Linear(self.inner_dim, self.d_model, bias=False)if self.has_relative_attention_bias:self.relative_attention_bias = nn.Embedding(self.relative_attention_num_buckets, self.n_heads)self.pruned_heads = set()self.gradient_checkpointing = Falsedef prune_heads(self, heads):if len(heads) == 0:returnheads, index = find_pruneable_heads_and_indices(heads, self.n_heads, self.key_value_proj_dim, self.pruned_heads)# Prune linear layersself.q = prune_linear_layer(self.q, index)self.k = prune_linear_layer(self.k, index)self.v = prune_linear_layer(self.v, index)self.o = prune_linear_layer(self.o, index, dim=1)# Update hyper paramsself.n_heads = self.n_heads - len(heads)self.inner_dim = self.key_value_proj_dim * self.n_headsself.pruned_heads = self.pruned_heads.union(heads)@staticmethoddef _relative_position_bucket(relative_position, bidirectional=True, num_buckets=32, max_distance=128):"""Adapted from Mesh Tensorflow:https://github.com/tensorflow/mesh/blob/0cb87fe07da627bf0b7e60475d59f95ed6b5be3d/mesh_tensorflow/transformer/transformer_layers.py#L593Translate relative position to a bucket number for relative attention. The relative position is defined asmemory_position - query_position, i.e. the distance in tokens from the attending position to the attended-toposition. If bidirectional=False, then positive relative positions are invalid. We use smaller buckets forsmall absolute relative_position and larger buckets for larger absolute relative_positions. All relativepositions >=max_distance map to the same bucket. All relative positions <=-max_distance map to the same bucket.This should allow for more graceful generalization to longer sequences than the model has been trained onArgs:relative_position: an int32 Tensorbidirectional: a boolean - whether the attention is bidirectionalnum_buckets: an integermax_distance: an integerReturns:a Tensor with the same shape as relative_position, containing int32 values in the range [0, num_buckets)"""relative_buckets = 0if bidirectional:num_buckets //= 2relative_buckets += (relative_position > 0).to(torch.long) * num_bucketsrelative_position = torch.abs(relative_position)else:relative_position = -torch.min(relative_position, torch.zeros_like(relative_position))# now relative_position is in the range [0, inf)# half of the buckets are for exact increments in positionsmax_exact = num_buckets // 2is_small = relative_position < max_exact# The other half of the buckets are for logarithmically bigger bins in positions up to max_distancerelative_position_if_large = max_exact + (torch.log(relative_position.float() / max_exact)/ math.log(max_distance / max_exact)* (num_buckets - max_exact)).to(torch.long)relative_position_if_large = torch.min(relative_position_if_large, torch.full_like(relative_position_if_large, num_buckets - 1))relative_buckets += torch.where(is_small, relative_position, relative_position_if_large)return relative_bucketsdef compute_bias(self, query_length, key_length, device=None):"""Compute binned relative position bias"""if device is None:device = self.relative_attention_bias.weight.devicecontext_position = torch.arange(query_length, dtype=torch.long, device=device)[:, None]memory_position = torch.arange(key_length, dtype=torch.long, device=device)[None, :]relative_position = memory_position - context_position # shape (query_length, key_length)relative_position_bucket = self._relative_position_bucket(relative_position, # shape (query_length, key_length)bidirectional=(not self.is_decoder),num_buckets=self.relative_attention_num_buckets,max_distance=self.relative_attention_max_distance,)values = self.relative_attention_bias(relative_position_bucket) # shape (query_length, key_length, num_heads)values = values.permute([2, 0, 1]).unsqueeze(0) # shape (1, num_heads, query_length, key_length)return valuesdef forward(self,hidden_states,mask=None,key_value_states=None,position_bias=None,past_key_value=None,layer_head_mask=None,query_length=None,use_cache=False,output_attentions=False,):"""Self-attention (if key_value_states is None) or attention over source sentence (provided by key_value_states)."""# Input is (batch_size, seq_length, dim)# Mask is (batch_size, key_length) (non-causal) or (batch_size, key_length, key_length)# past_key_value[0] is (batch_size, n_heads, q_len - 1, dim_per_head)batch_size, seq_length = hidden_states.shape[:2]real_seq_length = seq_lengthif past_key_value is not None:assert (len(past_key_value) == 2), f"past_key_value should have 2 past states: keys and values. Got { len(past_key_value)} past states"real_seq_length += past_key_value[0].shape[2] if query_length is None else query_lengthkey_length = real_seq_length if key_value_states is None else key_value_states.shape[1]def shape(states):"""projection"""return states.view(batch_size, -1, self.n_heads, self.key_value_proj_dim).transpose(1, 2)def unshape(states):"""reshape"""return states.transpose(1, 2).contiguous().view(batch_size, -1, self.inner_dim)def project(hidden_states, proj_layer, key_value_states, past_key_value):"""projects hidden states correctly to key/query states"""if key_value_states is None:# self-attn# (batch_size, n_heads, seq_length, dim_per_head)hidden_states = shape(proj_layer(hidden_states))elif past_key_value is None:# cross-attn# (batch_size, n_heads, seq_length, dim_per_head)hidden_states = shape(proj_layer(key_value_states))if past_key_value is not None:if key_value_states is None:# self-attn# (batch_size, n_heads, key_length, dim_per_head)hidden_states = torch.cat([past_key_value, hidden_states], dim=2)else:# cross-attnhidden_states = past_key_valuereturn hidden_states# get query statesquery_states = shape(self.q(hidden_states)) # (batch_size, n_heads, seq_length, dim_per_head)# get key/value stateskey_states = project(hidden_states, self.k, key_value_states, past_key_value[0] if past_key_value is not None else None)value_states = project(hidden_states, self.v, key_value_states, past_key_value[1] if past_key_value is not None else None)# compute scoresscores = torch.matmul(query_states, key_states.transpose(3, 2)) # equivalent of torch.einsum("bnqd,bnkd->bnqk", query_states, key_states), compatible with onnx op>9if position_bias is None:if not self.has_relative_attention_bias:position_bias = torch.zeros((1, self.n_heads, real_seq_length, key_length), device=scores.device, dtype=scores.dtype)if self.gradient_checkpointing and self.training:position_bias.requires_grad = Trueelse:position_bias = self.compute_bias(real_seq_length, key_length, device=scores.device)# if key and values are already calculated# we want only the last query position biasif past_key_value is not None:position_bias = position_bias[:, :, -hidden_states.size(1) :, :]if mask is not None:mask = mask.to('cuda')position_bias = position_bias + mask # (batch_size, n_heads, seq_length, key_length)if self.pruned_heads:mask = torch.ones(position_bias.shape[1])mask[list(self.pruned_heads)] = 0position_bias_masked = position_bias[:, mask.bool()]else:position_bias_masked = position_biasscores += position_bias_maskedattn_weights = nn.functional.softmax(scores.float(), dim=-1).type_as(scores) # (batch_size, n_heads, seq_length, key_length)attn_weights = nn.functional.dropout(attn_weights, p=self.dropout, training=self.training) # (batch_size, n_heads, seq_length, key_length)# Mask heads if we want toif layer_head_mask is not None:attn_weights = attn_weights * layer_head_maskattn_output = unshape(torch.matmul(attn_weights, value_states)) # (batch_size, seq_length, dim)attn_output = self.o(attn_output)present_key_value_state = (key_states, value_states) if (self.is_decoder and use_cache) else Noneoutputs = (attn_output,) + (present_key_value_state,) + (position_bias,)if output_attentions:outputs = outputs + (attn_weights,)return outputs
● 删减版的 T5Attention 代码(不影响后文讲解),后文说的 “代码” 都是说的这个:
class T5Attention(nn.Module):def __init__(self, config: T5Config):super().__init__()self.is_decoder = config.is_decoderself.d_model = config.d_modelself.key_value_proj_dim = config.d_kvself.n_heads = config.num_headsself.dropout = config.dropout_rateself.inner_dim = self.n_heads * self.key_value_proj_dim# Mesh TensorFlow initialization to avoid scaling before softmaxself.q = nn.Linear(self.d_model, self.inner_dim, bias=False)self.k = nn.Linear(self.d_model, self.inner_dim, bias=False)self.v = nn.Linear(self.d_model, self.inner_dim, bias=False)self.o = nn.Linear(self.inner_dim, self.d_model, bias=False)def forward(self,hidden_states,key_value_states=None,position_bias=None,past_key_value=None,layer_head_mask=None,query_length=None,use_cache=False,output_attentions=False,):def shape(states):return states.view(batch_size, -1, self.n_heads, self.key_value_proj_dim).transpose(1, 2)def unshape(states):return states.transpose(1, 2).contiguous().view(batch_size, -1, self.inner_dim)# Input is (batch_size, seq_length, dim)batch_size, seq_length = hidden_states.shape[:2]# get query statesquery_states = shape(self.q(hidden_states)) # (batch_size, n_heads, seq_length, dim_per_head)# get key/value stateskey_states = shape(self.k(hidden_states)) # (batch_size, n_heads, seq_length, dim_per_head)value_states = shape(self.v(hidden_states)) # (batch_size, n_heads, seq_length, dim_per_head)# compute scoresscores = torch.matmul(query_states, key_states.transpose(3, 2)) # equivalent of torch.einsum("bnqd,bnkd->bnqk", query_states, key_states), compatible with onnx op>9attn_weights = nn.functional.softmax(scores.float(), dim=-1).type_as(scores) # (batch_size, n_heads, seq_length, key_length)attn_weights = nn.functional.dropout(attn_weights, p=self.dropout, training=self.training) # (batch_size, n_heads, seq_length, key_length)attn_output = unshape(torch.matmul(attn_weights, value_states)) # (batch_size, seq_length, dim)attn_output = self.o(attn_output)return attn_output
二、一些灵魂问题,能回答上吗?
- Attention 的输入(input)是什么?输出(output)是什么?
- Attention 中的输入(input)与 “Q、K、V” 是啥关系?
- Attention 中的 Q、K、V 分别有什么含义?
- Attention 的计算流程是怎么样的?
- 多头 Attention 有什么用?
- 请介绍一下 Cross-Attention?
注:后面所有模型的 config 均是 T5 模型的默认配置,写出来是为了方便解释。
1. Attention 的输入是什么?输出是什么?
答:Attention 的输入(input)是文本特征 hidden_states,形式上是一个批次(batch_size)的特征张量。假如批次(batch_size)是 4,最大文本处理长度(max_length)为 512,特征维度(d_model)为 768,则输入 hidden_states 的形状即为 (4, 512, 768)。输出也是一个张量,形状和输出一样。
2. Attention 中的输入(input)与 “Q、K、V” 是啥关系?
答:我首先解释一下 “输入(input)与它们仨的关系”。将上面的代码截取出下面一段。因为 self.q、self.k 和 self.v 分别是三个不同的 nn.Linear(self.d_model, self.inner_dim, bias=False),即线性层,其中 self.d_model 为通用特征维度 768 (就是各个 Attention 模块传递的时候需要统一的特征维度);self.inner_dim 为 Attention 内部特征维度 768(就是该 Attention 模块内部用到的特征维度)。故 nn.Linear(self.d_model, self.inner_dim, bias=False) 即为 768×768 的神经网络,并包含偏置 nn.Linear(768, 768, bias=False)。
所以,输入(input)和 “Q、K、V” 之间存在一种映射关系。输入(input)通过三个不同的 768×768 的神经网络,映射成了三个不一样的特征张量,而这三个不一样的特征张量的形状依然为 (4, 512, 768) (这里承接了第一问的 “假如”,后面几问都是这样的)。
# get query states
query_states = shape(self.q(hidden_states)) # (batch_size, n_heads, seq_length, dim_per_head)# get key/value states
key_states = shape(self.k(hidden_states)) # (batch_size, n_heads, seq_length, dim_per_head)
value_states = shape(self.v(hidden_states)) # (batch_size, n_heads, seq_length, dim_per_head)
这里外带解释一下 shape() 是用来干嘛的。它是一个 “形状转换器”,把一个张量转换为 “多头张量”,并不改变里面的内容,只改变形状。通俗一点来讲就是把一个张量扩充一个维度,并将张量中的所有项分摊到这个维度中。
def shape(states):return states.view(batch_size, -1, self.n_heads, self.key_value_proj_dim).transpose(1, 2)
举个例子:假如输入(input)是一个形状为 (4, 512, 768) 的张量,即 hidden_states = Tensor{(4, 512, 768)}。假如 Q = self.q(hidden_states) = Tensor{(4, 512, 768)}(注意 self.q(hidden_states) ≠ hidden_states)。然后 query_states = shape(Q) = Q.view(batch_size, -1, self.n_heads, self.key_value_proj_dim).transpose(1, 2) = Q.view(4, -1, 12, 64).transpose(1, 2) = Tensor{(4, 512, 12, 64)}.transpose(1, 2) = Tensor{(4, 12, 512, 64)}
其中,self.n_heads 表示多头注意力机制中头的数量,T5 模型默认是 12。self.key_value_proj_dim 表示每个头里面的特征维度,T5 模型默认是 64。
3. Attention 中的 Q、K、V 分别有什么含义?
答:为了便于解释,下面以李宏毅课程中的 self-attention 例子来展开,先走一遍计算流程:
假如输入(input)是一句只有四个字的句子:“你好世界”,那我们进行分词(tokenizer)后会得到 [“你”, “好”, “世”, “界”]。(为了便于解释,后面我省去了 Embedding 操作,直接进行 Attention)接着呢, q 1 q^1 q1 = self.q(“你”), k 1 k^1 k1 = self.k(“你”), v 1 v^1 v1 = self.v(“你”); q 2 q^2 q2 = self.k(“好”), k 2 k^2 k2 = self.k(“好”), v 2 v^2 v2 = self.v(“好”);依次类推…
接着再计算 α 1 , 1 \alpha_{1,1} α1,1= q 1 × k 1 q^1\times k^1 q1×k1; α 1 , 2 \alpha_{1,2} α1,2= q 1 × k 2 q^1\times k^2 q1×k2;依次类推…(需注意的是 α x , 随意 \alpha_{x,随意} αx,随意 均是对第 x x x 个字进行处理。另外,常规的 Attention 还有除以 d \sqrt{d} d 的操作,这里为了方便讲解,省去了。后面的公式会再加上的)
然后将 α 1 , 1 \alpha_{1,1} α1,1、 α 1 , 2 \alpha_{1,2} α1,2、 α 1 , 3 \alpha_{1,3} α1,3 和 α 1 , 4 \alpha_{1,4} α1,4 进行归一化,即代码里面的 nn.functional.softmax() 操作,得到 α ^ 1 , 1 \hat \alpha_{1,1} α^1,1 = α 1 , 1 ∑ i n = 4 α 1 , i \frac{\alpha_{1,1}}{\sum_{i}^{n=4}\alpha_{1,i}} ∑in=4α1,iα1,1; α ^ 1 , 2 \hat \alpha_{1,2} α^1,2 = α 1 , 2 ∑ i n = 4 α 1 , i \frac{\alpha_{1,2}}{\sum_{i}^{n=4}\alpha_{1,i}} ∑in=4α1,iα1,2;依次类推…
接着计算 b 1 b^1 b1 = ∑ j n = 4 α ^ 1 , j × v j \sum_{j}^{n=4}\hat \alpha_{1,j}\times v^j ∑jn=4α^1,j×vj = α ^ 1 , 1 × v 1 + α ^ 1 , 2 × v 2 + α ^ 1 , 3 × v 3 + α ^ 1 , 4 × v 4 \hat \alpha_{1,1} \times v^1 + \hat \alpha_{1,2} \times v^2 + \hat \alpha_{1,3} \times v^3+ \hat \alpha_{1,4} \times v^4 α^1,1×v1+α^1,2×v2+α^1,3×v3+α^1,4×v4

以上的计算是针对 b 1 b^1 b1 的计算。接下来还要进行 b 2 b^2 b2、 b 3 b^3 b3 和 b 4 b^4 b4 的计算。计算过程都差不多,接下来就只介绍 b 1 b^1 b1 的计算了:(注意,上面图中的 α ^ \hat \alpha α^ 和下图中的 α ′ \alpha' α′ 表示都是同一个意思。还有就是下图的 a 1 a_1 a1、 a 2 a_2 a2、 a 3 a_3 a3 和 a 4 a_4 a4 可以分别理解为 “你”、“好”、“世” 和 “界” 四个字)
α 2 , 1 \alpha_{2,1} α2,1= q 2 × k 1 q^2\times k^1 q2×k1; α 2 , 2 \alpha_{2,2} α2,2= q 2 × k 2 q^2\times k^2 q2×k2;依次类推…
α ^ 2 , 1 \hat \alpha_{2,1} α^2,1 = α 2 , 1 ∑ i n = 4 α 2 , i \frac{\alpha_{2,1}}{\sum_{i}^{n=4}\alpha_{2,i}} ∑in=4α2,iα2,1; α ^ 2 , 2 \hat \alpha_{2,2} α^2,2 = α 2 , 2 ∑ i n = 4 α 2 , i \frac{\alpha_{2,2}}{\sum_{i}^{n=4}\alpha_{2,i}} ∑in=4α2,iα2,2;依次类推…
b 2 b^2 b2 = ∑ j n = 4 α ^ 2 , j × v j \sum_{j}^{n=4}\hat \alpha_{2,j}\times v^j ∑jn=4α^2,j×vj = α ^ 2 , 1 × v 1 + α ^ 2 , 2 × v 2 + α ^ 2 , 3 × v 3 + α ^ 2 , 4 × v 4 \hat \alpha_{2,1} \times v^1 + \hat \alpha_{2,2} \times v^2 + \hat \alpha_{2,3} \times v^3+ \hat \alpha_{2,4} \times v^4 α^2,1×v1+α^2,2×v2+α^2,3×v3+α^2,4×v4

最后,经过一些计算,得到的 b 1 b^{1} b1、 b 2 b^2 b2、 b 3 b^3 b3 和 b 4 b^4 b4 即分别是 “你”、“好”、“世” 和 “界” 的输出(output)。
乍一看,好像就那样,不就是把每个字进行三次不同的神经网络映射,然后每个字得到三个不同的副本“Q、K、V”,接着将每个字的 “副本Q” 与 自身以及其他字的 “副本K” 进行相乘,再将结果归一化,得到 “注意力分布”,然后再将这个 “注意力分布” 与自身以及其他字的 “副本V” 进行相乘,即得到每个字的 “注意力分数”。
OK,讲完计算流程后,现在咱们来一起深剖 Q、K、V 的含义 !
我们这样想,假如我现在来计算 [“你”, “好”, “世”, “界”] 中 “世” 字的 “注意力分数”。那么,Q 就代表我们读到的该字的一种 “基本意义”,我们能自然而然的想到 “世界、世代、世纪、出世、逝世、人世间” 等等;而 K 则代表在整个句子(或整篇文章)里面该字更倾向的含义——> “世界、人世间”等等(因为每个字的 K 会与其他字的 Q 进行联系计算,梯度更新时,K 的网络会进行更新,就会稍微加深 “联系”);最后,V 就要抽象一点理解了,我们可以把它理解为某一个人(不同人,他的阅历不同,看到这个字就会有不同的感受)的脑海里对于这个字的 “感觉”,可能是 “平淡的”,也可能是 “温暖的”、“喜爱的”、“反感的” 等等,或许还会有薛之谦的 “世界和平” 的感觉,反正代表了一种引申意。(这段解释只是笔者个人理解后的想法哈,在后面的 Cross-Attention 机制我会换一种观点来理解)
我没做过实验,但是我推断,当对某一文本数据集进行学习时,“Q、K、V” 的三个网络,应该 “V的网络” 更新得最慢,因为它更像是一种 “底层价值观网络”。而 “Q的网络” 更新得最快,因为不同的句子,相同的字出现不同的含义的频率很高。
最后,我在这里埋一个伏笔,“注意力分布” 就是 Q的各个字 与 K的各个字 之间两两的一种 “关联性分数”,关联性越强,分数越高。我会在后面的计算流程再一次提到这一点。
OK,理解完 Q、K、V 的含义后,我们再简单来举个例子,假如我们输入下面这句话给 T5 模型(输入给 ChatGPT 也是一样的),最后模型的输出会是什么呢?怎么推理的呢?
我刚买了一个苹果,感觉它非常好吃。请问刚刚我吃了什么?
显然,T5 模型的注意力会更多地放在 “苹果” 和 “它” 两字上面,它俩的 “q 和 k” 相乘的 “注意力分布” 将会很大,因为 “它” 被我吃了,而 “它” 与 “苹果” 联系性最强,故答案是 “苹果”。
4. Attention 的计算流程是怎么样的?
答:虽然我在 “3. Attention 中的 Q、K、V 分别有什么含义?” 里已经介绍过了 Attention 的计算流程,但那只是一部分。完整的计算流程还得看代码(超简化版,包含所有的关键步骤):
def forward(self, hidden_states, key_value_states=None, position_bias=None, past_key_value=None, layer_head_mask=None, query_length=None, use_cache=False, output_attentions=False,):def shape(states): # 作用: 将某一个张量的形状从 (batch_size, seq_length, d_model) 转化为 (batch_size, n_heads, seq_length, dim_per_head)return states.view(batch_size, -1, self.n_heads, self.key_value_proj_dim).transpose(1, 2)def unshape(states): # 作用: 将某一个张量的形状从 (batch_size, n_heads, seq_length, dim_per_head) 转化为 (batch_size, seq_length, d_model)return states.transpose(1, 2).contiguous().view(batch_size, -1, self.inner_dim)batch_size, seq_length = hidden_states.shape[:2] # hidden_states 是一个张量 {Tensor(4, 512, 768)}query_states = shape(self.q(hidden_states)) # 计算出 Q, 并转化为多头, 得到 {Tensor(4, 12, 512, 64)}key_states = shape(self.k(hidden_states)) # 计算出 K, 并转化为多头, 得到 {Tensor(4, 12, 512, 64)}value_states = shape(self.v(hidden_states)) # 计算出 V, 并转化为多头, 得到 {Tensor(4, 12, 512, 64)}scores = torch.matmul(query_states, key_states.transpose(3, 2)) # 计算 “注意力分布” {Tensor()}, {Tensor(4, 12, 512, 64)} × {Tensor(4, 12, 64, 512)} → {Tensor(4, 12, 512, 512)}attn_weights = nn.functional.softmax(scores.float(), dim=-1).type_as(scores) # softmax操作(即归一化操作)attn_weights = nn.functional.dropout(attn_weights, p=self.dropout, training=self.training) # dropout操作(防止过拟合)attn_output = unshape(torch.matmul(attn_weights, value_states)) # 先进行矩阵相乘 {Tensor(4, 12, 512, 512)} × {Tensor(4, 12, 512, 64)} → {Tensor(4, 12, 512, 64)}, 再将多头特征融合起来. {Tensor(4, 12, 512, 64)} → {Tensor(4, 512, 768)}attn_output = self.o(attn_output) # 最后经过一个线性层, 得到的结果仍然是一个张量 {Tensor(4, 512, 768)}return attn_output
注意!!!! 我为了便于解释,并着重讲解 Attention 机制,上面的代码便省略了 掩码(Mask)的操作 以及 相对位置信息的嵌入(position_bias),后面有机会,我再写篇博客讲讲它们。
简单来说,Attention 的所有计算都是在矩阵的基础上(也可以说是在张量的基础上进行的),并没有像我之前写的那样一个一个地计算: α 1 , 1 \alpha_{1,1} α1,1= q 1 × k 1 q^1\times k^1 q1×k1、 α 1 , 2 \alpha_{1,2} α1,2= q 1 × k 2 q^1\times k^2 q1×k2,但是计算结果都是一样的,只不过矩阵计算更方便,也能够加快计算速度(其中 d \sqrt{d} d 一般就是模型默认的特征维度 d_model,即 768):
a = q × k ⊺ d = [ q 1 q 2 q 3 q 4 ] × [ k 1 k 2 k 3 k 4 ] d = [ a 1 , 1 a 1 , 2 ⋯ a 1 , 4 a 2 , 1 a 2 , 2 ⋯ a 2 , 4 ⋮ ⋮ ⋱ ⋮ a 4 , 1 a 4 , 2 ⋯ a 4 , 4 ] \boldsymbol{a}=\frac{\boldsymbol{q}\times \boldsymbol{k}^{\intercal}}{\sqrt{d}}=\frac{\\ \left[ \begin{matrix} q_1 \\ q_2 \\ q_3 \\ q_4\end{matrix}\right] \times \left[ \begin{matrix} k_1\,\, k_2 \,\,k_3 \,\,k_4\end{matrix}\right] \\}{\sqrt{d}} = \left[ \begin{matrix} a_{1,1}& a_{1,2}& \cdots& a_{1,4}\\ a_{2,1}& a_{2,2}& \cdots& a_{2,4}\\ \vdots& \vdots& \ddots& \vdots\\ a_{4,1}& a_{4,2}& \cdots& a_{4,4}\\ \end{matrix} \right] a=dq×k⊺=d q1q2q3q4 ×[k1k2k3k4]= a1,1a2,1⋮a4,1a1,2a2,2⋮a4,2⋯⋯⋱⋯a1,4a2,4⋮a4,4
α = softmax ( a ) = [ a 1 , 1 ′ a 1 , 2 ′ ⋯ a 1 , 4 ′ a 2 , 1 ′ a 2 , 2 ′ ⋯ a 2 , 4 ′ ⋮ ⋮ ⋱ ⋮ a 4 , 1 ′ a 4 , 2 ′ ⋯ a 4 , 4 ′ ] , a i , j ′ = exp ( a i , j ) ∑ j = 1 n = 4 exp ( a i , j ) \boldsymbol{\alpha }=\text{softmax} \left( \boldsymbol{a} \right) =\left[ \begin{matrix} a'_{1,1}& a'_{1,2}& \cdots& a'_{1,4}\\ a'_{2,1}& a'_{2,2}& \cdots& a'_{2,4}\\ \vdots& \vdots& \ddots& \vdots\\ a'_{4,1}& a'_{4,2}& \cdots& a'_{4,4}\\ \end{matrix} \right] ,\quad a'_{i,j}=\frac{\exp \left( a_{i,j} \right)}{\sum_{j=1}^{n=4}{\exp}\left( a_{i,j} \right)} α=softmax(a)= a1,1′a2,1′⋮a4,1′a1,2′a2,2′⋮a4,2′⋯⋯⋱⋯a1,4′a2,4′⋮a4,4′ ,ai,j′=∑j=1n=4exp(ai,j)exp(ai,j)
b = α × v = [ a 1 , 1 ′ a 1 , 2 ′ ⋯ a 1 , 4 ′ a 2 , 1 ′ a 2 , 2 ′ ⋯ a 2 , 4 ′ ⋮ ⋮ ⋱ ⋮ a 4 , 1 ′ a 4 , 2 ′ ⋯ a 4 , 4 ′ ] × [ v 1 v 2 v 3 v 4 ] = [ b 1 b 2 b 3 b 4 ] \boldsymbol{b}=\boldsymbol{\alpha }\times \boldsymbol{v} = \left[ \begin{matrix} a'_{1,1}& a'_{1,2}& \cdots& a'_{1,4}\\ a'_{2,1}& a'_{2,2}& \cdots& a'_{2,4}\\ \vdots& \vdots& \ddots& \vdots\\ a'_{4,1}& a'_{4,2}& \cdots& a'_{4,4}\\ \end{matrix} \right] \times \left[ \begin{matrix} v_1 \\ v_2 \\ v_3 \\ v_4\end{matrix}\right] = \left[ \begin{matrix} b_1 \\ b_2 \\ b_3\\b_4\end{matrix}\right] b=α×v= a1,1′a2,1′⋮a4,1′a1,2′a2,2′⋮a4,2′⋯⋯⋱⋯a1,4′a2,4′⋮a4,4′ × v1v2v3v4 = b1b2b3b4
代码里在计算出上述的 b \boldsymbol{b} b 后,其实还有 dropout 的操作,这是为了防止过拟合。另外最后还要经过一个线性层得到最终的输出 output \text{output} output = self.o( b \boldsymbol{b} b ),其中 self.o() = nn.Linear(768, 768, bias=False)。至于为什么要加这个线性层呢?或许这就是神经网络的玄学了,层数多一点,记忆的东西更深刻一点?…
OK,在这里我揭晓刚刚埋的伏笔。从矩阵 α \boldsymbol{\alpha } α 的形状可以看出,它是 4×4 的,也就是说,它就是 Q版本的[“你”, “好”, “世”, “界”] 与 K版本的[“你”, “好”, “世”, “界”] 的各个字之间两两的一种 “关联性分数”。如果 Q版本的[“你”, “好”, “世”, “界”] "世"字 对 K版本的[“你”, “好”, “世”, “界”]的"界"字 在模型看来很有关系,那么 a 3 , 4 ′ a'_{3,4} a3,4′ 相较其他 “注意力分布”的分数 将会比较大。
5. 多头 Attention 有什么用?
答:先讲讲多头 Attention 的计算流程吧:就是我们把原本一个句子(比如刚刚说的“你好世界”)中的某个字(比如“世”字)的 768 维的特征(即 [1.2563, -5.2934, 0.0567, -0.8004, 3.0503, …, 0.2502] ←我随便写的,总共 768 个表示特征的数字)分成 N 个子特征(假如 N = 12,则子特征的维度即为 head_d_model = 768/12 = 64),就得到了 N 个包含 768/N 个特征数的子特征。
这个原理和 计算机视觉(CV)领域的卷积神经核的原理 类似吧,我感觉,都是为了让特征的计算更 “细腻” 或者更 “粗糙” 。不同的卷积核大小,3×3 或者 5×5 或者 1×1 等等,卷积得到的特征是不一样的,显然,卷积核尺寸越大卷积得到的特征越 “精”;卷积核尺寸越小卷积得到的特征越 “泛”。那么,多头的头数越多,那么文本在进行 “注意力分布” 计算时,某一字就能被划分成更多层的含义(比如 12 层含义),然后与另一个同样具有多层含义的字进行乘积计算,这样得到的多个特征会更 “全面” 一点。
6. 请介绍一下 Cross-Attention?
答:Cross-Attention 即是交叉注意力机制。之前讲的所有例子其实都是 Self-Attention 机制,也就是某一段文本与其自身进行 “自注意力” 的计算,并没有涉及到一段文本与另一段文本的 “交叉注意力” 的计算。
我们先来理一下 Cross-Attention 的计算流程:
假如我们用下面的 句子① 对 句子② 进行 Cross-Attention(注意!!!!先后关系很重要,谁在前就是前者,谁在后就是后者,谁对的谁,顺序很重要)。
① 李华英语考试不及格,告诉妈妈他出去找同学玩了。
② 小明去超市门口和李华汇合,他俩说了好多话。
那么, q \boldsymbol q q 就是 句子① 经过 self.q() 得到的, k \boldsymbol k k 和 v \boldsymbol v v 就是 句子② 分别经过 self.k() 和 self.v() 得到的。其中,句子① 的长度为 23,句子② 的长度为 21。那么:
a = q × k ⊺ d = [ q 1 q 2 ⋮ q 23 ] × [ k 1 k 2 ⋯ k 21 ] d = [ a 1 , 1 a 1 , 2 ⋯ a 1 , 21 a 2 , 1 a 2 , 2 ⋯ a 2 , 21 ⋮ ⋮ ⋱ ⋮ a 23 , 1 a 23 , 2 ⋯ a 23 , 21 ] ∈ R 23 × 21 \boldsymbol{a}=\frac{\boldsymbol{q}\times \boldsymbol{k}^{\intercal}}{\sqrt{d}}=\frac{\\ \left[ \begin{matrix} q_1 \\ q_2 \\ \vdots \\ q_{23}\end{matrix}\right] \times \left[ \begin{matrix} k_1\,\, k_2 \,\, \cdots \,\,k_{21}\end{matrix}\right] \\}{\sqrt{d}} = \left[ \begin{matrix} a_{1,1}& a_{1,2}& \cdots& a_{1,21}\\ a_{2,1}& a_{2,2}& \cdots& a_{2,21}\\ \vdots& \vdots& \ddots& \vdots\\ a_{23,1}& a_{23,2}& \cdots& a_{23,21}\\ \end{matrix} \right] \in \mathbb{R}^{23 \times 21} a=dq×k⊺=d q1q2⋮q23 ×[k1k2⋯k21]= a1,1a2,1⋮a23,1a1,2a2,2⋮a23,2⋯⋯⋱⋯a1,21a2,21⋮a23,21 ∈R23×21
α = softmax ( a ) = [ a 1 , 1 ′ a 1 , 2 ′ ⋯ a 1 , 21 ′ a 2 , 1 ′ a 2 , 2 ′ ⋯ a 2 , 21 ′ ⋮ ⋮ ⋱ ⋮ a 23 , 1 ′ a 23 , 2 ′ ⋯ a 23 , 21 ′ ] , a i , j ′ = exp ( a i , j ) ∑ j = 1 n = 21 exp ( a i , j ) \boldsymbol{\alpha }=\text{softmax} \left( \boldsymbol{a} \right) =\left[ \begin{matrix} a'_{1,1}& a'_{1,2}& \cdots& a'_{1,21}\\ a'_{2,1}& a'_{2,2}& \cdots& a'_{2,21}\\ \vdots& \vdots& \ddots& \vdots\\ a'_{23,1}& a'_{23,2}& \cdots& a'_{23,21}\\ \end{matrix} \right] ,\quad a'_{i,j}=\frac{\exp \left( a_{i,j} \right)}{\sum_{j=1}^{n=21}{\exp}\left( a_{i,j} \right)} α=softmax(a)= a1,1′a2,1′⋮a23,1′a1,2′a2,2′⋮a23,2′⋯⋯⋱⋯a1,21′a2,21′⋮a23,21′ ,ai,j′=∑j=1n=21exp(ai,j)exp(ai,j)
b = α × v = [ a 1 , 1 ′ a 1 , 2 ′ ⋯ a 1 , 21 ′ a 2 , 1 ′ a 2 , 2 ′ ⋯ a 2 , 21 ′ ⋮ ⋮ ⋱ ⋮ a 23 , 1 ′ a 23 , 2 ′ ⋯ a 23 , 21 ′ ] × [ v 1 v 2 ⋮ v 21 ] = [ b 1 b 2 ⋮ b 23 ] ∈ R 23 × 1 \boldsymbol{b}=\boldsymbol{\alpha }\times \boldsymbol{v} = \left[ \begin{matrix} a'_{1,1}& a'_{1,2}& \cdots& a'_{1,21}\\ a'_{2,1}& a'_{2,2}& \cdots& a'_{2,21}\\ \vdots& \vdots& \ddots& \vdots\\ a'_{23,1}& a'_{23,2}& \cdots& a'_{23,21}\\ \end{matrix} \right] \times \left[ \begin{matrix} v_1 \\ v_2 \\ \vdots\\ v_{21}\end{matrix}\right] = \left[ \begin{matrix} b_1 \\ b_2 \\ \vdots \\b_{23}\end{matrix}\right] \in \mathbb{R}^{23 \times 1} b=α×v= a1,1′a2,1′⋮a23,1′a1,2′a2,2′⋮a23,2′⋯⋯⋱⋯a1,21′a2,21′⋮a23,21′ × v1v2⋮v21 = b1b2⋮b23 ∈R23×1
最后再进行 dropout 操作并经过最后一个线性层 self.o() 即得到输出。(注意!!!!虽然我在图中写的是 R 23 × 1 \mathbb{R}^{23 \times 1} R23×1,但其实更严谨的写法是 R 23 × 768 \mathbb{R}^{23 \times 768} R23×768,因为 b 1 b_1 b1、 b 2 b_2 b2、 b 3 b_3 b3 和 b 4 b_4 b4 其实都是 768 维的向量。如果再加上 batch_size (= 4 的话),那么就是 R 4 × 23 × 768 \mathbb{R}^{4\times 23 \times 768} R4×23×768)
OK,计算过程理完了。那 Cross-Attention 机制的精髓在哪里呢? 就在对 “Q、K、V” 的分配里。如果是句子①对句子②进行 Cross-Attention(谁对谁,前者后者关系很重要),那么 Q 就是 句子① 经过 self.q() 的映射;K 是 句子② 经过 self.k() 的映射;V 是 句子② 经过 self.v() 的映射。为啥单单 Q 来自于句子①?因为我们是要用句子① 对照着 句子② 进行分析,那么句子①更像是一种查询(Query),而句子②更像是一种 “字典”,这个字典包含了众多的 “键(Key)-值(Value)-对”。我们带着查询(Query),也可以说是带着一种 “询问”,来翻这个 “字典”,一一比对这个 “字典” 里面的各个 “键(Key)”,然后琢磨琢磨其 “值(Value)”——在这里,值(Value)可以理解为字典中对某一个字的详细阐释。(这段解释也只是笔者个人理解后的想法哈,和前面的 (Self-)Attention 机制的理解有点不同)
另外,当我们想用 句子② 对 句子① 进行 Cross-Attention,也可以。只不过中间得到的 “注意力分布矩阵” 的大小会发生变化,变为 R 21 × 23 \mathbb{R}^{21 \times 23} R21×23,最后 b \boldsymbol{b} b 的大小也会变为 R 21 × 1 \mathbb{R}^{21 \times 1} R21×1。
最后,我们再来看看 Cross-Attention 的代码吧,还是用上 T5 模型的代码进行演示(简化版):
def forward(self, hidden_states, key_value_states=None, position_bias=None, past_key_value=None, layer_head_mask=None, query_length=None, use_cache=False, output_attentions=False,):def shape(states): # 作用: 将某一个张量的形状从 (batch_size, seq_length, d_model) 转化为 (batch_size, n_heads, seq_length, dim_per_head)return states.view(batch_size, -1, self.n_heads, self.key_value_proj_dim).transpose(1, 2)def unshape(states): # 作用: 将某一个张量的形状从 (batch_size, n_heads, seq_length, dim_per_head) 转化为 (batch_size, seq_length, d_model)return states.transpose(1, 2).contiguous().view(batch_size, -1, self.inner_dim)batch_size, seq_length = hidden_states.shape[:2] # hidden_states 是一个张量 {Tensor(4, 512, 768)}query_states = shape(self.q(hidden_states)) # 计算出 Q, 并转化为多头, 得到 {Tensor(4, 12, 512, 64)}key_states = shape(self.k(key_value_states)) # 计算出 K, 并转化为多头, 得到 {Tensor(4, 12, 512, 64)}value_states = shape(self.v(key_value_states)) # 计算出 V, 并转化为多头, 得到 {Tensor(4, 12, 512, 64)}scores = torch.matmul(query_states, key_states.transpose(3, 2)) # 计算 “注意力分布” {Tensor()}, {Tensor(4, 12, 512, 64)} × {Tensor(4, 12, 64, 512)} → {Tensor(4, 12, 512, 512)}attn_weights = nn.functional.softmax(scores.float(), dim=-1).type_as(scores) # softmax操作(即归一化操作)attn_weights = nn.functional.dropout(attn_weights, p=self.dropout, training=self.training) # dropout操作(防止过拟合)attn_output = unshape(torch.matmul(attn_weights, value_states)) # 先进行矩阵相乘 {Tensor(4, 12, 512, 512)} × {Tensor(4, 12, 512, 64)} → {Tensor(4, 12, 512, 64)}, 再将多头特征融合起来. {Tensor(4, 12, 512, 64)} → {Tensor(4, 512, 768)}attn_output = self.o(attn_output) # 最后经过一个线性层, 得到的结果仍然是一个张量 {Tensor(4, 512, 768)}return attn_output
与之前 (Self-)Attention 机制的代码差不多,只有 key_states 和 value_states 不同。
三、补充说明
● 若有写得 不对/不妥 的地方,或有疑问,欢迎评论交流。
● 前面买了一些坑,比如。省略了 掩码(Mask)的操作、 d \sqrt d d 以及 相对位置信息的嵌入(position_bias) 的说明,后面写博客再补上吧,今天就写到这里…
● 调侃:感觉…刚上研究生,感觉我好懒,花了三天,才断断续续写完这篇博客哈哈哈哈哈[/手动狗头]…
⭐️ ⭐️ ⭐️
相关文章:

对Transformer中的Attention(注意力机制)的一点点探索
摘要:本文试图对 Transformer 中的 Attention 机制进行一点点探索。并就 6 个问题深入展开。 ✅ NLP 研 1 选手的学习笔记 简介:小王,NPU,2023级,计算机技术 研究方向:文本生成、摘要生成 文章目录 一、为啥…...

车内信息安全技术-安全技术栈-软件安全
操作系统 1.隔离技术 信息安全中的隔离技术通常指的是将不同安全级别的信息或数据隔离开来,以保护敏感信息不受未授权的访问或泄露。在操作系统中,常见的隔离技术包括:虚拟化技术:通过虚拟化软件,将物理计算机分割成多个独立的虚拟计算机,每个虚拟计算机都可以运行独立的…...

Redis常见命令
命令可以查看的文档 http://doc.redisfans.com/ https://redis.io/commands/ 官方文档(英文) http://www.redis.cn/commands.html 中文 https://redis.com.cn/commands.html 个人推荐这个 https://try.redis.io/ redis命令在线测试工具 https://githubfa…...
Android Studio实现一笔画完小游戏
文章目录 一、项目概述二、开发环境三、详细设计3.1、数据库设计3.2、普通模式3.3、随机模式3.4、关卡列表 四、运行演示五、项目总结六、源码获取 一、项目概述 Android一笔画完是一种益智游戏,玩家需要从起点开始通过一条连续的线,将图形中所有的方块…...

【Python 程序设计】数据人员入门【02/8】
一、说明 介绍如何管理 Python 依赖项和一些虚拟环境最佳实践。 以下文章是有关 Python 数据工程系列文章的一部分,旨在帮助数据工程师、数据科学家、数据分析师、机器学习工程师或其他刚接触 Python 的人掌握基础知识。迄今为止,本初学者指南包括&#…...
学习笔记——树上哈希
普通子树哈希 树上的很多东西都是转化成链上问题的,比如树上哈希 树上哈希,主要是用于树的同构这个东西上的 什么是树的同构? 如图,不考虑节点编号,三棵树是同构的 将树转化成链,一般有两种方式…...
Opencv快速入门教程,Python计算机视觉基础
快速入门 OpenCV 是 Intel 开源计算机视觉库。它由一系列 C 函数和少量 C 类构成, 实现了图像处理和计算机视觉方面的很多通用算法。 OpenCV 拥有包括 300 多个 C 函数的跨平台的中、高层 API。它不依赖于其它的外部库——尽管也 可以使用某些外部库。 OpenCV 对非…...

laravel 报错误信息 Carbon\Exceptions\InvalidFormatException
Carbon\Exceptions\InvalidFormatException Unexpected data found. at vendor\nesbot\carbon\src\Carbon\Traits\Creator.php:687 683▕ return $instance; 684▕ } 685▕ 686▕ if (static::isStrictModeEnabled()) { ➜ 687…...
UI自动化之混合框架
什么是混合框架,混合框架就是将数据驱动与关键字驱动结合在一起,主要用来回归业务主流程,将核心流程串联起来。 上一篇我们写到了关键字驱动框架,关键字驱动框架是针对一个业务场景的单条测试用例的。 我们以163邮箱的登录到创建…...
)
SQL创建用户-非DM8.2环境(达梦数据库)
DM8:达梦数据库SQL创建用户-非DM8.2环境 环境介绍 环境介绍 在没有图形化界面,或者想快速创建用户,可以使用一下SQL语句;将其中的 CESHI 替换为要创建的用户名即可,默认创建了数据表空间,索引表空间,文件大…...

Thread类中run和start的区别
答:调用线程类中的 start 方法,才开始创建并启动线程,而线程被回收,则是要执行完线程的入口方法(对于主线程来说,则是要执行完 main 方法),这里要回收线程则是要将(&…...

ElementUI浅尝辄止35:Checkbox 多选框
一组备选项中进行多选 1.如何使用? 单独使用可以表示两种状态之间的切换,写在标签中的内容为 checkbox 按钮后的介绍。 //在el-checkbox元素中定义v-model绑定变量,单一的checkbox中,默认绑定变量的值会是Boolean,选…...

讲讲如何用IDEA开发java项目——本文来自AI创作助手
使用IDEA开发Java项目,您可以按照以下步骤进行操作: 下载并安装IntelliJ IDEA 您可以从JetBrains官网下载并安装最新版的IntelliJ IDEA。 创建项目 启动IDEA,在欢迎界面中选择“Create New Project”或者在主菜单中选择“File”->“Ne…...
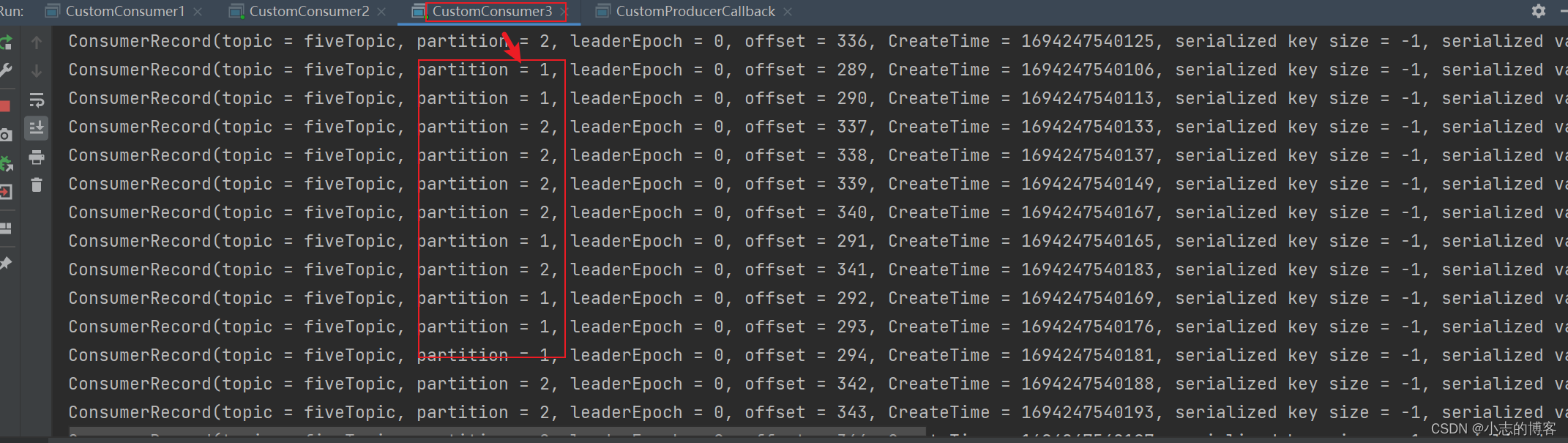
Kafka3.0.0版本——消费者(Range分区分配策略以及再平衡)
目录 一、Range分区分配策略原理1.1、Range分区分配策略原理的示例一1.2、Range分区分配策略原理的示例二1.3、Range分区分配策略原理的示例注意事项 二、Range 分区分配策略代码案例2.1、创建带有4个分区的fiveTopic主题2.2、创建三个消费者 组成 消费者组2.3、创建生产者2.4、…...

WeiTools
目录 1.1 WeiTools 1.2 getTime 1.3 getImageView 1.4 StringEncode 1.4.1 // TODO Auto-generated catch block WeiTools package com.shrimp.xiaoweirobot.tools;...
)
目标检测数据集:医学图像检测数据集(自己标注)
1.专栏介绍 ✨✨✨✨✨✨目标检测数据集✨✨✨✨✨✨ 本专栏提供各种场景的数据集,主要聚焦:工业缺陷检测数据集、小目标数据集、遥感数据集、红外小目标数据集,该专栏的数据集会在多个专栏进行验证,在多个数据集进行验证mAP涨点明显,尤其是小目标、遮挡物精度提升明显的…...
【系统设计系列】数据库
系统设计系列初衷 System Design Primer: 英文文档 GitHub - donnemartin/system-design-primer: Learn how to design large-scale systems. Prep for the system design interview. Includes Anki flashcards. 中文版: https://github.com/donnemarti…...
mp4压缩视频不改变画质?跟我这样压缩视频大小
在当今数字化时代,视频文件变得越来越普遍,然而,这些文件通常都很大,给存储和传输带来了困难,为了解决这个问题,许多人都希望将视频压缩得更小,而又不牺牲画质,下面就来看看具体应该…...

AQS同步队列和等待队列的同步机制
理解AQS必须要理解同步队列和等待队列之间的同步机制,简单来说流程是: 获取锁失败的线程进入同步队列,成功的占用锁,占锁线程调用await方法进入条件等待队列,其他占锁线程调用signal方法,条件等待队列线程进…...

vue3实现无限循环滚动的方法;el-table内容无限循环滚动的实现
需求:vue3实现一个div内的内容无限循环滚动 方法一: <template><div idcontainer><div class"item" v-foritem in 5>测试内容{{{ item }}</div></div> </template><script setup> //封装一个方法…...

conda相比python好处
Conda 作为 Python 的环境和包管理工具,相比原生 Python 生态(如 pip 虚拟环境)有许多独特优势,尤其在多项目管理、依赖处理和跨平台兼容性等方面表现更优。以下是 Conda 的核心好处: 一、一站式环境管理:…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

第25节 Node.js 断言测试
Node.js的assert模块主要用于编写程序的单元测试时使用,通过断言可以提早发现和排查出错误。 稳定性: 5 - 锁定 这个模块可用于应用的单元测试,通过 require(assert) 可以使用这个模块。 assert.fail(actual, expected, message, operator) 使用参数…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现录音机应用
1. 项目配置与权限设置 1.1 配置module.json5 {"module": {"requestPermissions": [{"name": "ohos.permission.MICROPHONE","reason": "录音需要麦克风权限"},{"name": "ohos.permission.WRITE…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

学习STC51单片机32(芯片为STC89C52RCRC)OLED显示屏2
每日一言 今天的每一份坚持,都是在为未来积攒底气。 案例:OLED显示一个A 这边观察到一个点,怎么雪花了就是都是乱七八糟的占满了屏幕。。 解释 : 如果代码里信号切换太快(比如 SDA 刚变,SCL 立刻变&#…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

Spring AI Chat Memory 实战指南:Local 与 JDBC 存储集成
一个面向 Java 开发者的 Sring-Ai 示例工程项目,该项目是一个 Spring AI 快速入门的样例工程项目,旨在通过一些小的案例展示 Spring AI 框架的核心功能和使用方法。 项目采用模块化设计,每个模块都专注于特定的功能领域,便于学习和…...
