【补】代码随想录算法训练营day38|动态规划 |509. 斐波那契数|70. 爬楼梯|746. 使用最小花费爬楼梯
动态规划,英文:Dynamic Programming,简称DP,如果某一问题有很多重叠子问题,使用动态规划是最有效的。所以动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心,贪心没有状态推导,而是从局部直接选最优的。
动态规划的解题步骤
状态转移公式(递推公式)是很重要,但动规不仅仅只有递推公式。
对于动态规划问题,我将拆解为如下五步曲,这五步都搞清楚了,才能说把动态规划真的掌握了!
- 确定dp数组(dp table)以及下标的含义
- 确定递推公式
- dp数组如何初始化
- 确定遍历顺序
- 举例推导dp数组
一些同学可能想为什么要先确定递推公式,然后在考虑初始化呢?
因为一些情况是递推公式决定了dp数组要如何初始化!
动态规划应该如何debug
找问题的最好方式就是把dp数组打印出来,看看究竟是不是按照自己思路推导的!
一些同学对于dp的学习是黑盒的状态,就是不清楚dp数组的含义,不懂为什么这么初始化,递推公式背下来了,遍历顺序靠习惯就是这么写的,然后一鼓作气写出代码,如果代码能通过万事大吉,通过不了的话就凭感觉改一改。
这是一个很不好的习惯!
做动规的题目,写代码之前一定要把状态转移在dp数组的上具体情况模拟一遍,心中有数,确定最后推出的是想要的结果。
然后再写代码,如果代码没通过就打印dp数组,看看是不是和自己预先推导的哪里不一样。
如果打印出来和自己预先模拟推导是一样的,那么就是自己的递归公式、初始化或者遍历顺序有问题了。
如果和自己预先模拟推导的不一样,那么就是代码实现细节有问题。
这样才是一个完整的思考过程,而不是一旦代码出问题,就毫无头绪的东改改西改改,最后过不了,或者说是稀里糊涂的过了。
这也是我为什么在动规五步曲里强调推导dp数组的重要性。
举个例子哈:在「代码随想录」刷题小分队微信群里,一些录友可能代码通过不了,会把代码抛到讨论群里问:我这里代码都已经和题解一模一样了,为什么通过不了呢?
发出这样的问题之前,其实可以自己先思考这三个问题:
- 这道题目我举例推导状态转移公式了么?
- 我打印dp数组的日志了么?
- 打印出来了dp数组和我想的一样么?
如果这灵魂三问自己都做到了,基本上这道题目也就解决了,或者更清晰的知道自己究竟是哪一点不明白,是状态转移不明白,还是实现代码不知道该怎么写,还是不理解遍历dp数组的顺序。
然后在问问题,目的性就很强了,群里的小伙伴也可以快速知道提问者的疑惑了。
注意这里不是说不让大家问问题哈, 而是说问问题之前要有自己的思考,问题要问到点子上!
509. 斐波那契数
力扣题目链接
斐波那契数,通常用 F(n) 表示,形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是: F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1 给你n ,请计算 F(n) 。
示例 1:
- 输入:2
- 输出:1
- 解释:F(2) = F(1) + F(0) = 1 + 0 = 1
示例 2:
- 输入:3
- 输出:2
- 解释:F(3) = F(2) + F(1) = 1 + 1 = 2
示例 3:
- 输入:4
- 输出:3
- 解释:F(4) = F(3) + F(2) = 2 + 1 = 3
提示:
动规五部曲:
这里我们要用一个一维dp数组来保存递归的结果
- 确定dp数组以及下标的含义
dp[i]的定义为:第i个数的斐波那契数值是dp[i]
- 确定递推公式
为什么这是一道非常简单的入门题目呢?
因为题目已经把递推公式直接给我们了:状态转移方程 dp[i] = dp[i - 1] + dp[i - 2];
- dp数组如何初始化
题目中把如何初始化也直接给我们了,如下:
dp[0] = 0;
dp[1] = 1;
1.确定遍历顺序
从递归公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,dp[i]是依赖 dp[i - 1] 和 dp[i - 2],那么遍历的顺序一定是从前到后遍历的
2.举例推导dp数组
按照这个递推公式dp[i] = dp[i - 1] + dp[i - 2],我们来推导一下,当N为10的时候,dp数组应该是如下的数列:
0 1 1 2 3 5 8 13 21 34 55
如果代码写出来,发现结果不对,就把dp数组打印出来看看和我们推导的数列是不是一致的。
以上我们用动规的方法分析完了,代码如下:
class Solution {public int fib(int n) {if(n<=1) return n;int[] dp=new int[n+1];dp[0]=0;dp[1]=1;for(int i=2;i<=n;i++){dp[i]=dp[i-1]+dp[i-2];}return dp[n];}
}
- 时间复杂度:O(n)
- 空间复杂度:O(n)
当然可以发现,我们只需要维护两个数值就可以了,不需要记录整个序列。
代码如下:
class Solution {public int fib(int n) {if (n < 2) return n;int a = 0, b = 1, c = 0;for (int i = 1; i < n; i++) {c = a + b;a = b;b = c;}return c;}
}
- 时间复杂度:O(n)
- 空间复杂度:O(1)
70. 爬楼梯
力扣题目链接
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
示例 1:
- 输入: 2
- 输出: 2
- 解释: 有两种方法可以爬到楼顶。
- 1 阶 + 1 阶
- 2 阶
示例 2:
- 输入: 3
- 输出: 3
- 解释: 有三种方法可以爬到楼顶。
- 1 阶 + 1 阶 + 1 阶
- 1 阶 + 2 阶
- 2 阶 + 1 阶
我们来分析一下,动规五部曲:
定义一个一维数组来记录不同楼层的状态
1.确定dp数组以及下标的含义
dp[i]: 爬到第i层楼梯,有dp[i]种方法
2.确定递推公式
dp[i] 可以有两个方向推出来。
首先是dp[i - 1],上i-1层楼梯,有dp[i - 1]种方法,那么再一步跳一个台阶不就是dp[i]了么。
还有就是dp[i - 2],上i-2层楼梯,有dp[i - 2]种方法,那么再一步跳两个台阶不就是dp[i]了么。
那么dp[i]就是 dp[i - 1]与dp[i - 2]之和!
所以dp[i] = dp[i - 1] + dp[i - 2] 。
3.dp数组如何初始化
再回顾一下dp[i]的定义:爬到第i层楼梯,有dp[i]种方法。
本题其实就不应该讨论dp[0]的初始化!
我相信dp[1] = 1,dp[2] = 2,这个初始化大家应该都没有争议的。
所以我的原则是:不考虑dp[0]如何初始化,只初始化dp[1] = 1,dp[2] = 2,然后从i = 3开始递推,这样才符合dp[i]的定义。
4.确定遍历顺序
从递推公式dp[i] = dp[i - 1] + dp[i - 2];中可以看出,遍历顺序一定是从前向后遍历的
5.举例推导dp数组
举例当n为5的时候,dp table(dp数组)应该是这样的
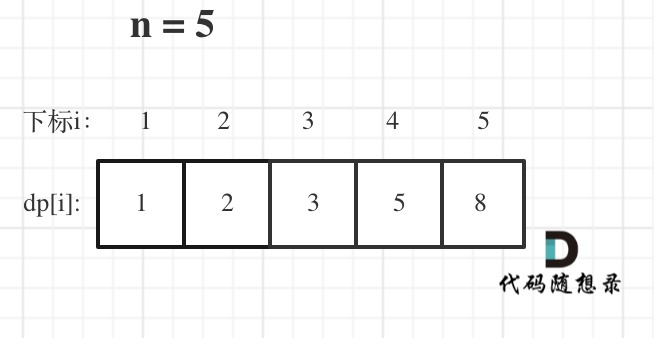
如果代码出问题了,就把dp table 打印出来,看看究竟是不是和自己推导的一样。
此时大家应该发现了,这不就是斐波那契数列么!
唯一的区别是,没有讨论dp[0]应该是什么,因为dp[0]在本题没有意义!
以上五部分析完之后,C++代码如下:
class Solution {public int climbStairs(int n) {if(n<=1) return n;int[] dp=new int[n+1];dp[1]=1;dp[2]=2;for(int i=3;i<=n;i++){dp[i]=dp[i-2]+dp[i-1];}return dp[n];}
}- 时间复杂度:O(n)
- 空间复杂度:O(n)
当然依然也可以,优化一下空间复杂度,代码如下:
class Solution {public int climbStairs(int n) {if(n<=1) return n;int a=1;int b=2;int sum=0;for(int i=3;i<=n;i++){sum=a+b;a=b;b=sum;}return b;}
}
- 时间复杂度: O ( n ) O(n) O(n)
- 空间复杂度: O ( 1 ) O(1) O(1)
746. 使用最小花费爬楼梯
力扣题目链接
数组的每个下标作为一个阶梯,第 i 个阶梯对应着一个非负数的体力花费值 cost[i](下标从 0 开始)。
每当你爬上一个阶梯你都要花费对应的体力值,一旦支付了相应的体力值,你就可以选择向上爬一个阶梯或者爬两个阶梯。
请你找出达到楼层顶部的最低花费。在开始时,你可以选择从下标为 0 或 1 的元素作为初始阶梯。
示例 1:
- 输入:cost = [10, 15, 20]
- 输出:15
- 解释:最低花费是从 cost[1] 开始,然后走两步即可到阶梯顶,一共花费 15 。
示例 2:
- 输入:cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1]
- 输出:6
- 解释:最低花费方式是从 cost[0] 开始,逐个经过那些 1 ,跳过 cost[3] ,一共花费 6 。
提示:
- cost 的长度范围是 [2, 1000]。
- cost[i] 将会是一个整型数据,范围为 [0, 999] 。
思路
(在力扣修改了题目描述下,我又重新修改了题解)
修改之后的题意就比较明确了,题目中说 “你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯” 也就是相当于 跳到 下标 0 或者 下标 1 是不花费体力的, 从 下标 0 下标1 开始跳就要花费体力了。
1.确定dp数组以及下标的含义
使用动态规划,就要有一个数组来记录状态,本题只需要一个一维数组dp[i]就可以了。
dp[i]的定义:到达第i台阶所花费的最少体力为dp[i]。
2.确定递推公式
可以有两个途径得到dp[i],一个是dp[i-1] 一个是dp[i-2]。
dp[i - 1] 跳到 dp[i] 需要花费 dp[i - 1] + cost[i - 1]。
dp[i - 2] 跳到 dp[i] 需要花费 dp[i - 2] + cost[i - 2]。
那么究竟是选从dp[i - 1]跳还是从dp[i - 2]跳呢?
一定是选最小的,所以dp[i] = min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);
3.dp数组如何初始化
新题目描述中明确说了 “你可以选择从下标为 0 或下标为 1 的台阶开始爬楼梯。” 也就是说 到达 第 0 个台阶是不花费的,但从 第0 个台阶 往上跳的话,需要花费 cost[0]。
所以初始化 dp[0] = 0,dp[1] = 0;
4.确定遍历顺序
因为是模拟台阶,而且dp[i]由dp[i-1]dp[i-2]推出,所以是从前到后遍历cost数组就可以了。
5.举例推导dp数组
拿示例2:cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1] ,来模拟一下dp数组的状态变化,如下:
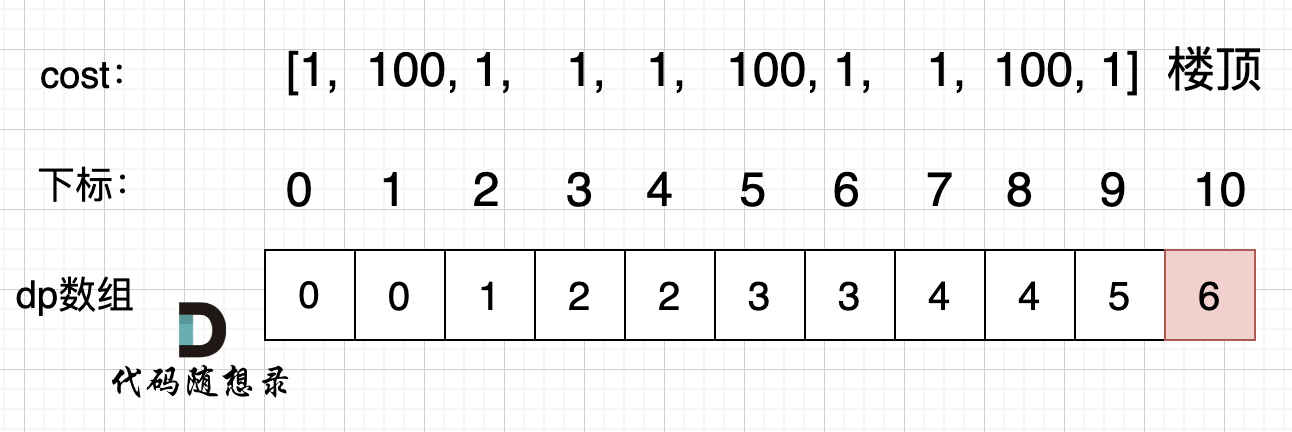
如果大家代码写出来有问题,就把dp数组打印出来,看看和如上推导的是不是一样的。
以上分析完毕,整体代码如下:
class Solution {public int minCostClimbingStairs(int[] cost) {int[] dp=new int[cost.length+1];dp[0]=0;dp[1]=0;for(int i=2;i<=cost.length;i++){dp[i]=Math.min(dp[i-1]+cost[i-1],dp[i-2]+cost[i-2]);}return dp[cost.length];}
}
- 时间复杂度:O(n)
- 空间复杂度:O(n)
还可以优化空间复杂度,因为dp[i]就是由前两位推出来的,那么也不用dp数组了,C++代码如下:
class Solution {public int minCostClimbingStairs(int[] cost) {int dp0=0;int dp1=0;for(int i=2;i<=cost.length;i++){int dpi=Math.min(dp1+cost[i-1],dp0+cost[i-2]);dp0=dp1;dp1=dpi;}return dp1;}
}
- 时间复杂度:O(n)
- 空间复杂度:O(1)
当然如果在面试中,能写出版本一就行,除非面试官额外要求 空间复杂度,那么再去思考版本二,因为版本二还是有点绕。版本一才是正常思路。
相关文章:

【补】代码随想录算法训练营day38|动态规划 |509. 斐波那契数|70. 爬楼梯|746. 使用最小花费爬楼梯
动态规划,英文:Dynamic Programming,简称DP,如果某一问题有很多重叠子问题,使用动态规划是最有效的。所以动态规划中每一个状态一定是由上一个状态推导出来的,这一点就区分于贪心,贪心没有状态推…...
C语言sizeof()计算空间大小为8的问题
在练习数据结构过程中,定义指针p,并且申请了10个char类型空间,但在计算p所指空间大小时候,发现了一些奇怪的现象。 #include <stdio.h> #include <stdlib.h>int main(){char s[12];printf("the size of memory …...
时序分解 | MATLAB实现基于LMD局部均值分解的信号分解分量可视化
时序分解 | MATLAB实现基于LMD局部均值分解的信号分解分量可视化 目录 时序分解 | MATLAB实现基于LMD局部均值分解的信号分解分量可视化效果一览基本介绍程序设计参考资料 效果一览 基本介绍 LMD局部均值分解 直接替换Excel即可运行包含频谱图相关系数图 Matlab语言 1.算法新颖…...

景区AR虚拟三维场景沉浸式体验成为新兴的营销手段
科技的迅速崛起正在改变我们的世界,旅游业也在这股浪潮中掀起了一场全新的变革。增强现实(AR)技术正成为旅行中的一股强大力量,通过增添趣味和交互性,为旅程注入了前所未有的活力。本文将带您深入了解AR如何为旅游带来全新的体验,…...
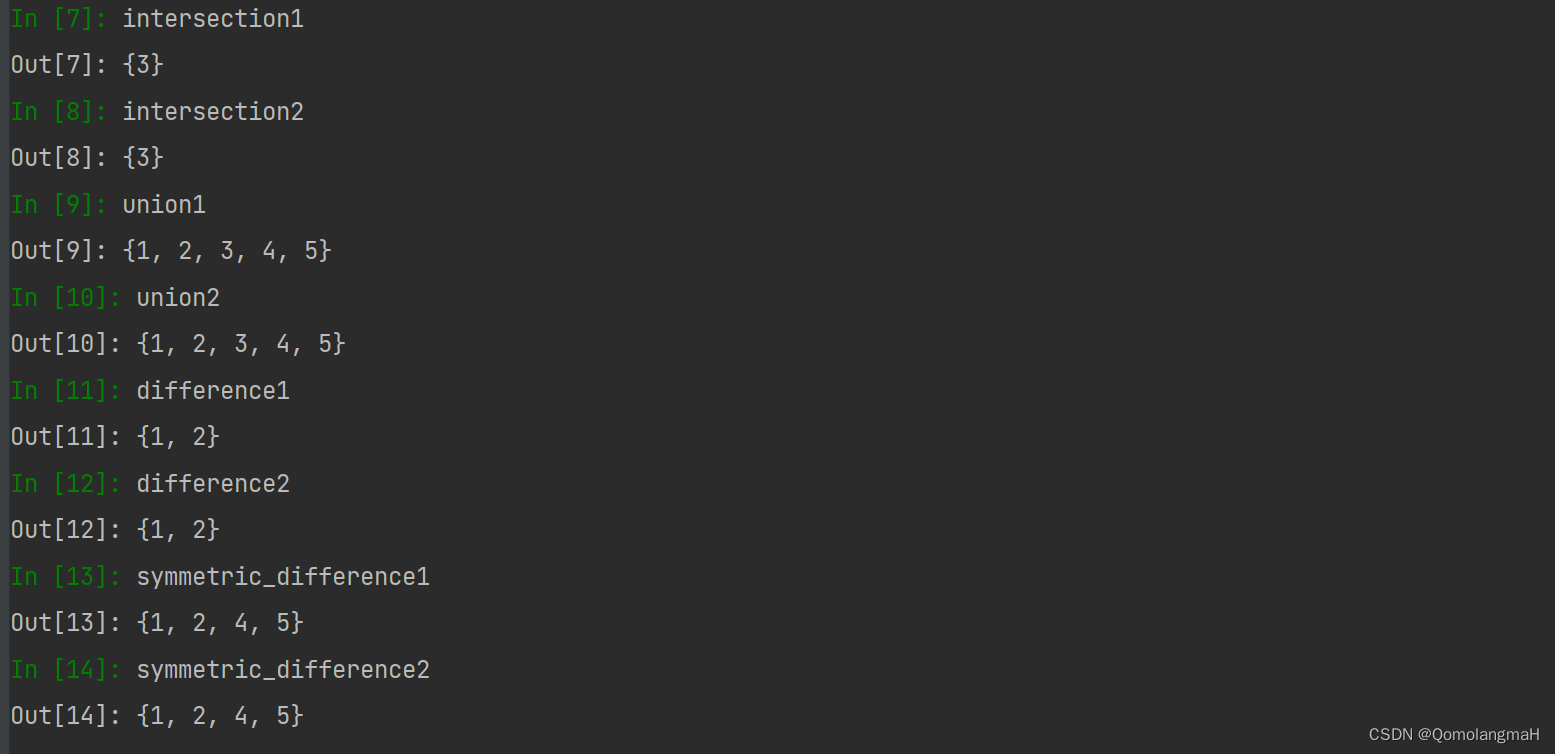
【深度学习】 Python 和 NumPy 系列教程(五):Python容器:3、集合Set详解(初始化、访问元素、常用操作、常用函数)
目录 一、前言 二、实验环境 三、Python容器(Containers) 0、容器介绍 1、列表(List) 2、元组(Tuple) 3、集合(Set) 1. 初始化 2. 访问集合元素 3. 常用操作 a. 添加单个…...

单片机C语言实例:6、定时器的应用
一、定时器0控制LED闪烁 实例程序1: #include<reg52.h> //包含头文件,一般情况不需要改动,头文件包含特殊功能寄存器的定义sbit LED P1^2; //定义LED端口/*------------------------------------------------定时器初始化子程序 …...

ChatGPT Prompting开发实战(五)
一、如何编写有效的prompt 对于大语言模型来说,编写出有效的prompt能够帮助模型更好地理解用户的意图(intents),生成针对用户提问来说是有效的答案,避免用户与模型之间来来回回对话多次但是用户不能从LLM那里得到有意义的反馈。本文通过具体…...

MySQL——DQL union合并、limit限制与DDL建表和删表
一、Union 合并 union:是实现两个查询结果的合并。 例如:当我们查询员工名字为manager 和 salesman的员工名字和 工作? select e.ename,e.job from emp e where e.jobmanager or e.job salesman; select e.ename,e.job from emp e where e.job in(man…...
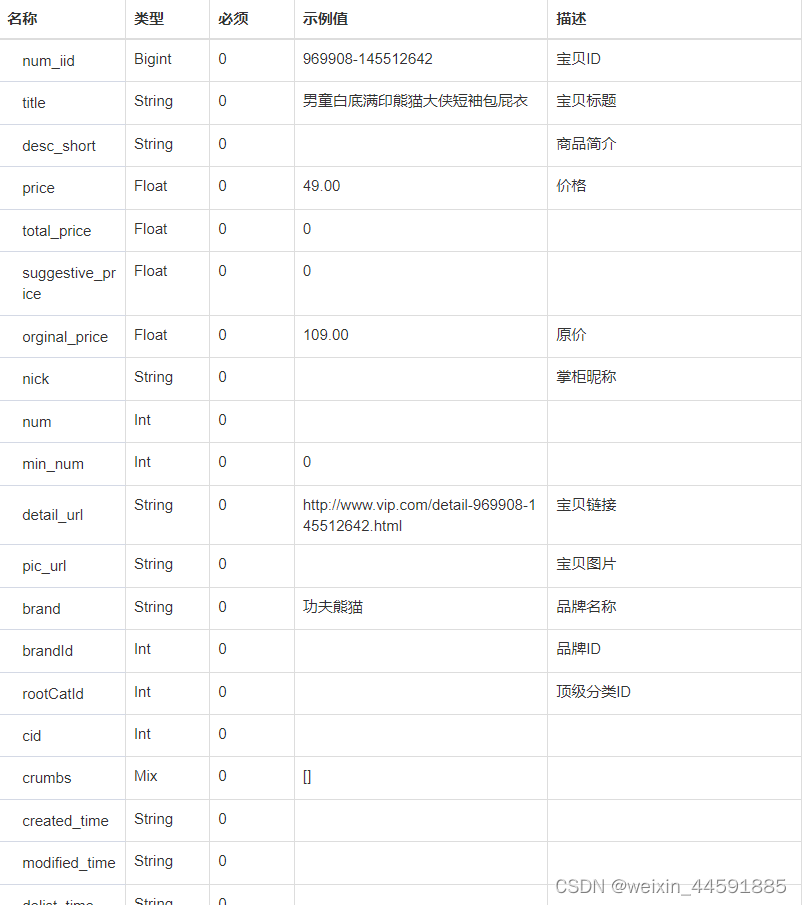
Java“牵手”唯品会商品列表数据,关键词搜索唯品会商品数据接口,唯品会API申请指南
唯品会商城是一个网上购物平台,售卖各类商品,包括服装、鞋类、家居用品、美妆产品、电子产品等。要获取唯品会商品列表和商品详情页面数据,您可以通过开放平台的接口或者直接访问唯品会商城的网页来获取商品详情信息。以下是两种常用方法的介…...
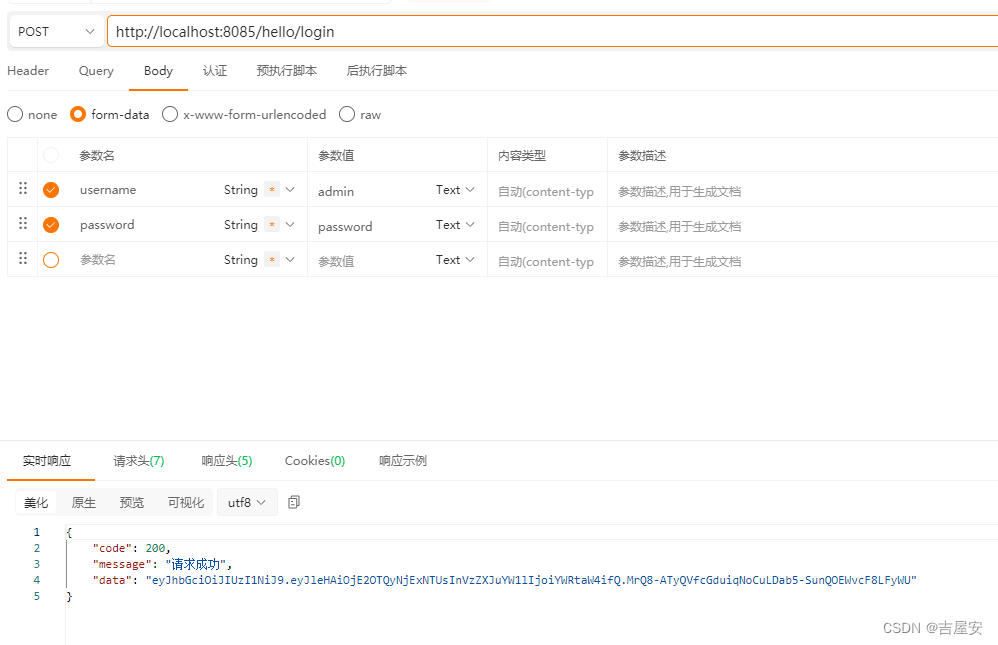
Springboot整合JWT完成验证登录
目录 一、引入依赖二、JwtUtil 代码解读三、LoginController 代码解读四、整体代码五、结果展示 一、引入依赖 <dependency><groupId>io.jsonwebtoken</groupId><artifactId>jjwt</artifactId><version>0.9.1</version></depende…...

centos7 下使用docker安装常见的软件:Redis
关于docker的基础知识,请见《别在说自己不知道docker了,全文通俗易懂的给你说明白docker的基础与底层原理》 在自己学习的过程中经常会需要动手安装一下常见的工具,本篇就手把手带你用docker安装一遍。 jdk安装 如果先要更换之前的jdk从第…...
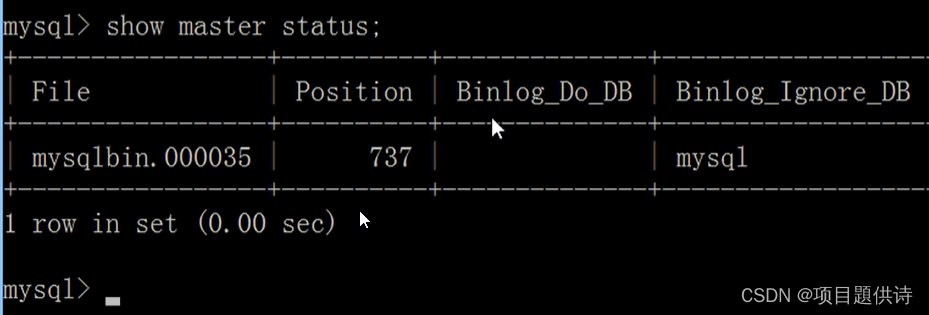
sql:SQL优化知识点记录(十五)
(1)MySQL主从复制 我们这里配置一Windows上的MySql做主机,Linux上的MySql做从机,搭建一主一从 测试以下是否能够拼通:从Linux上:167,连接Windows的165 从Windows的165 连接Linux上:…...

vue3+ts 分享海报
安装依赖1. npm install html2canvas --save<div class"flex-box"><div><div v-for"(item,index ) in from.list" :key"index" click"actvieFuntion(index)"><div>{{item}}</div><div :class"…...
Ubuntu23.10将推出全磁盘加密功能,提高系统安全性
Canonical 宣布其即将推出的 Ubuntu 23.10(Mantic Minotaur)将引入基于 TPM 的全磁盘加密的初步支持。这个特性将利用系统可信平台模块(TPM),在系统级别上进行全磁盘加密,从而提高系统的安全性。 但需要注…...

防火墙的设置主要是为了防范什么
防火墙的设置主要是为了防范网络攻击和数据泄露。随着互联网的普及和信息化的加速,网络安全问题越来越受到人们的关注。其中,防火墙是一种常见的网络安全设备,其设置的重要性也日益凸显。 防火墙的设置主要是为了防范什么 防火墙的设置主要目…...

Vim9和其他软件的文本复制、粘贴
大家都知道:在Vim9中使用y和p命令来进行文本的复制和粘贴,今天我来说一说Vim和其他软件之间的文本复制、粘贴操作。 Vim9和其他软件进行复制、粘贴,其原理就是通过系统剪贴板作为中介来执行操作。 一、从Vim9复制文本内容 按住鼠标左键滑出…...
MySQL学习5:事务、存储引擎
事务 简介 事务是一组数据库操作的执行单元,它要么完全执行,要么完全不执行。事务是确保数据库中的数据一致性和完整性的重要机制之一。 事务具有以下四个特性(称为ACID特性): 原子性(Atomicity…...

redis如何保证接口的幂等性
背景 如何防止接口中同样的数据提交,以及如何保证消息不被重复消费,这些都是shigen在学习的过程中遇到的问题。今天,趁着在学习redis的间隙,我写了一篇文章进行简单的实现。 注意:仅使用于单机的场景,对于…...

避坑之路 —— 前后端 json 的注意问题
当我们在进行开发项目的时候,在前后端需要进行数据之间的传输,那么就会需要到json。而json算是字符串中的一种 1.先说一下前端的, 其实这两种都是表示前端希望能收到后端json这样的数据格式,那么我们在后端就需要注意将数据进行转换为json进…...

[构建 Vue 组件库] 小尾巴 UI 组件库 —— 横向商品卡片(仿淘宝)
文章归档于:https://www.yuque.com/u27599042/row3c6 组件库地址 npm:https://www.npmjs.com/package/xwb-ui?activeTabreadmegitee:https://gitee.com/tongchaowei/xwb-ui 下载 npm i xwb-ui配置 按需导入 import {组件名 } from xwb-…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

应用升级/灾备测试时使用guarantee 闪回点迅速回退
1.场景 应用要升级,当升级失败时,数据库回退到升级前. 要测试系统,测试完成后,数据库要回退到测试前。 相对于RMAN恢复需要很长时间, 数据库闪回只需要几分钟。 2.技术实现 数据库设置 2个db_recovery参数 创建guarantee闪回点,不需要开启数据库闪回。…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

IT供电系统绝缘监测及故障定位解决方案
随着新能源的快速发展,光伏电站、储能系统及充电设备已广泛应用于现代能源网络。在光伏领域,IT供电系统凭借其持续供电性好、安全性高等优势成为光伏首选,但在长期运行中,例如老化、潮湿、隐裂、机械损伤等问题会影响光伏板绝缘层…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...

Kafka入门-生产者
生产者 生产者发送流程: 延迟时间为0ms时,也就意味着每当有数据就会直接发送 异步发送API 异步发送和同步发送的不同在于:异步发送不需要等待结果,同步发送必须等待结果才能进行下一步发送。 普通异步发送 首先导入所需的k…...
提供了哪些便利?)
现有的 Redis 分布式锁库(如 Redisson)提供了哪些便利?
现有的 Redis 分布式锁库(如 Redisson)相比于开发者自己基于 Redis 命令(如 SETNX, EXPIRE, DEL)手动实现分布式锁,提供了巨大的便利性和健壮性。主要体现在以下几个方面: 原子性保证 (Atomicity)ÿ…...

第7篇:中间件全链路监控与 SQL 性能分析实践
7.1 章节导读 在构建数据库中间件的过程中,可观测性 和 性能分析 是保障系统稳定性与可维护性的核心能力。 特别是在复杂分布式场景中,必须做到: 🔍 追踪每一条 SQL 的生命周期(从入口到数据库执行)&#…...

Vue3中的computer和watch
computed的写法 在页面中 <div>{{ calcNumber }}</div>script中 写法1 常用 import { computed, ref } from vue; let price ref(100);const priceAdd () > { //函数方法 price 1price.value ; }//计算属性 let calcNumber computed(() > {return ${p…...

Qt的学习(二)
1. 创建Hello Word 两种方式,实现helloworld: 1.通过图形化的方式,在界面上创建出一个控件,显示helloworld 2.通过纯代码的方式,通过编写代码,在界面上创建控件, 显示hello world; …...
