【Linux】管道
管道命令
#include <unistd.h>
int pipe(int pipefd[2]);
在Linux中,管道(pipe)的返回值是一个整数数组,包含两个文件描述符。这两个文件描述符分别代表管道的读端和写端。
当成功创建一个管道时,pipe()系统调用会返回0,并将文件描述符存储在提供的数组中。文件描述符是非负整数,通常是从3开始递增的。文件描述符中,索引为0的表示标准输入(stdin),索引为1的表示标准输出(stdout),索引为2的表示标准错误输出(stderr)。
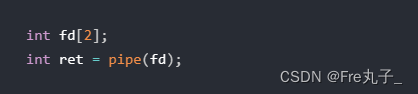
例如,如果使用以下代码创建了一个管道:
若创建成功,
ret的值将为0,fd数组的第一个元素fd[0]将为读端的文件描述符,fd数组的第二个元素fd[1]将为写端的文件描述符。
需要注意的是,创建管道失败时,pipe()系统调用会返回-1,并设置适当的错误码。在这种情况下,通过检查错误码可以确定具体的失败原因。
管道介绍
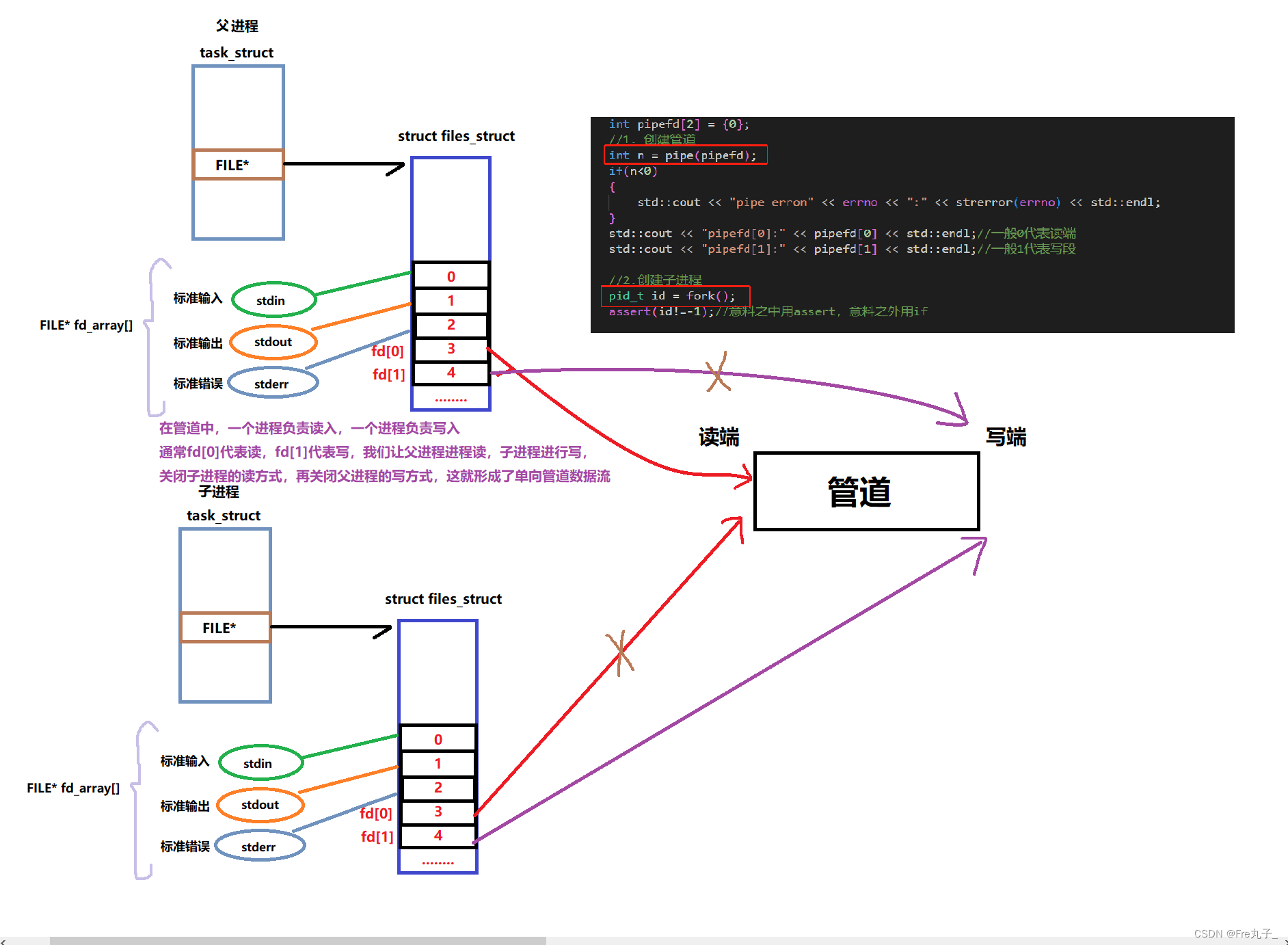
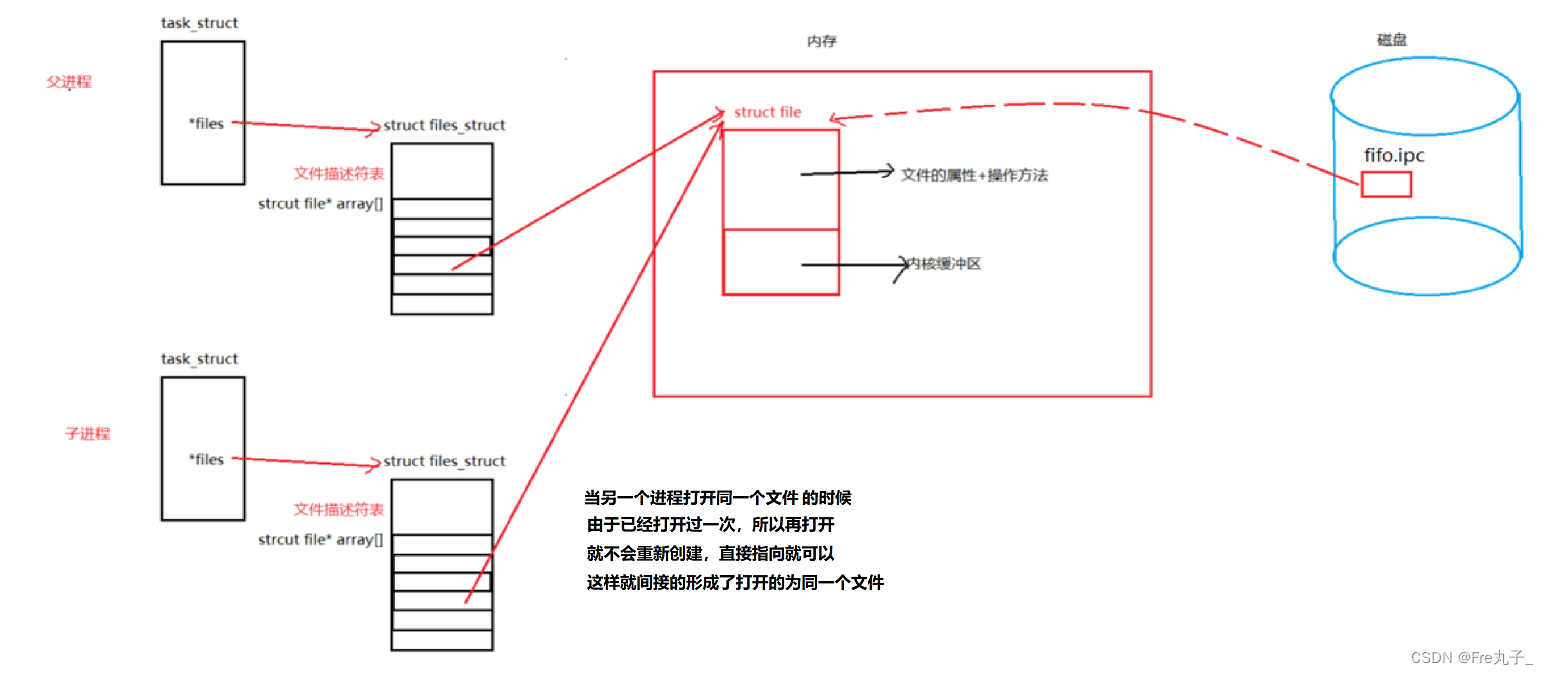
管道是一种单向数据流,它有一个读端和一个写端。
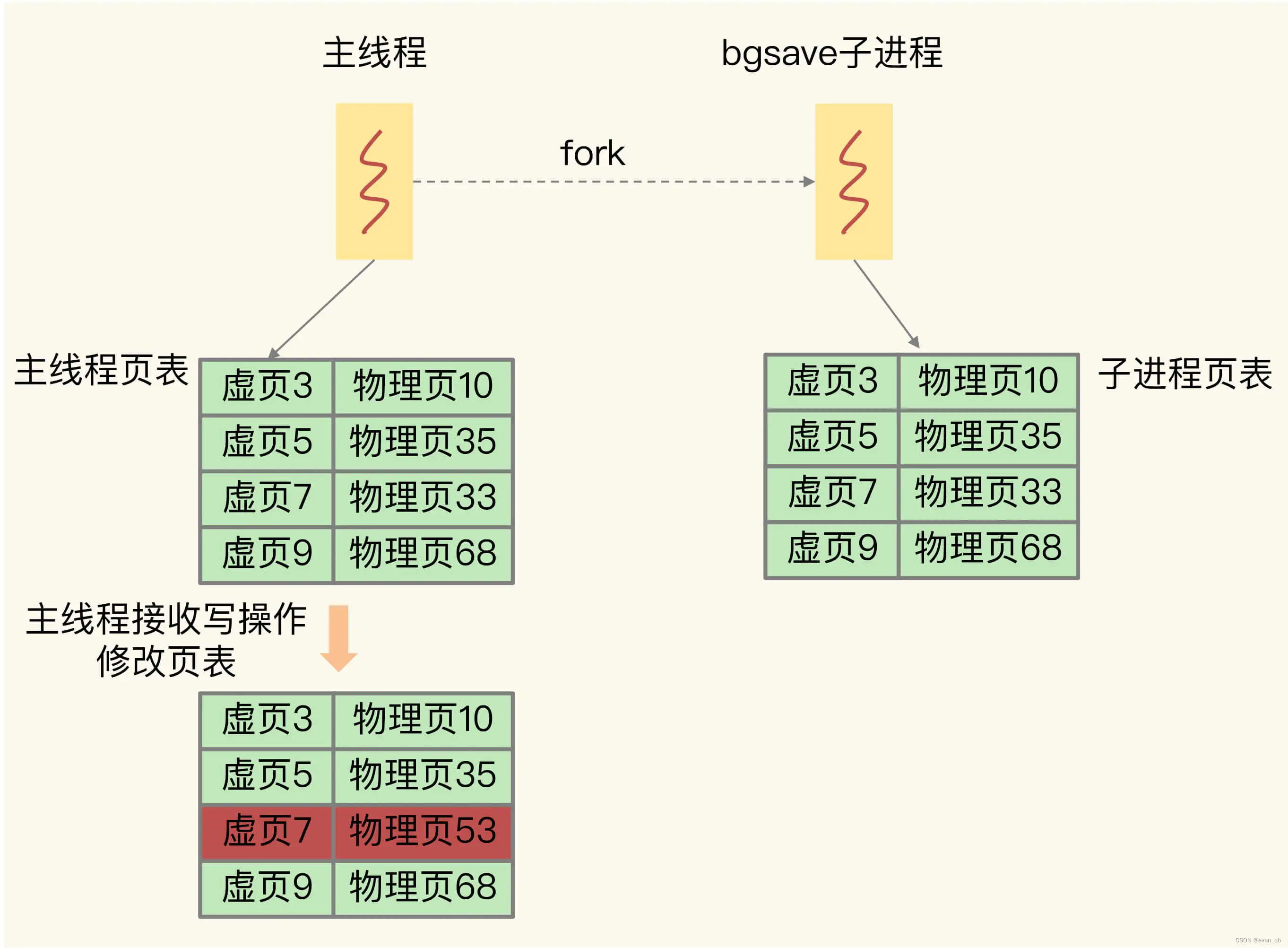
当父进程创建一个管道后,它会得到两个文件描述符,一个用于读取管道数据,一个用于写入管道数据。接着,父进程会创建一个子进程。子进程继承了父进程的文件描述符。
在Linux中,管道被称为半双工(half-duplex),这意味着它只能进行单向数据流的传输。具体而言,管道可以提供两个方向的数据流,一个是从写端到读端的方向,另一个是从读端到写端的方向。但是,不能同时在这两个方向上进行读写操作。
当父进程创建一个管道后,可以通过写端向管道中写入数据,然后通过读端从管道中读取数据。但是,父进程不能同时使用同一个管道进行读写操作。同样,子进程也可以使用同一个管道进行读写操作,但是也不能同时进行。
管道的特点
- 管道是单向同行的,也叫半双工
- 管道的本质是文件,因为fd的生命周期随进程,管道的生命周期也是随进程的
- 管道通信,通常用来进行具有“血缘”关系的进程,进行进程间通信。常用于父子通信。
- 在管道通信中,写入的次数和读取的次数,不是严格匹配的。
具有一定的协同能力,让read和write能按照一定的步骤进行通信
管道的四种场景
- 如果我们read读取完毕了所有管道数据,如果读端没有写入,那么写端就会一直等待
- 如果我们write端写满后,我们就会停止写入,直到读端读取数据后才可以正常写入
- 如果我们关闭了写端,当读端将写端最后的数据读取完再度取是就会返回0,表示已经读到了文件结尾。
- 如果写端一直写,读端关闭那么系统将直接通过kill -13进行终止
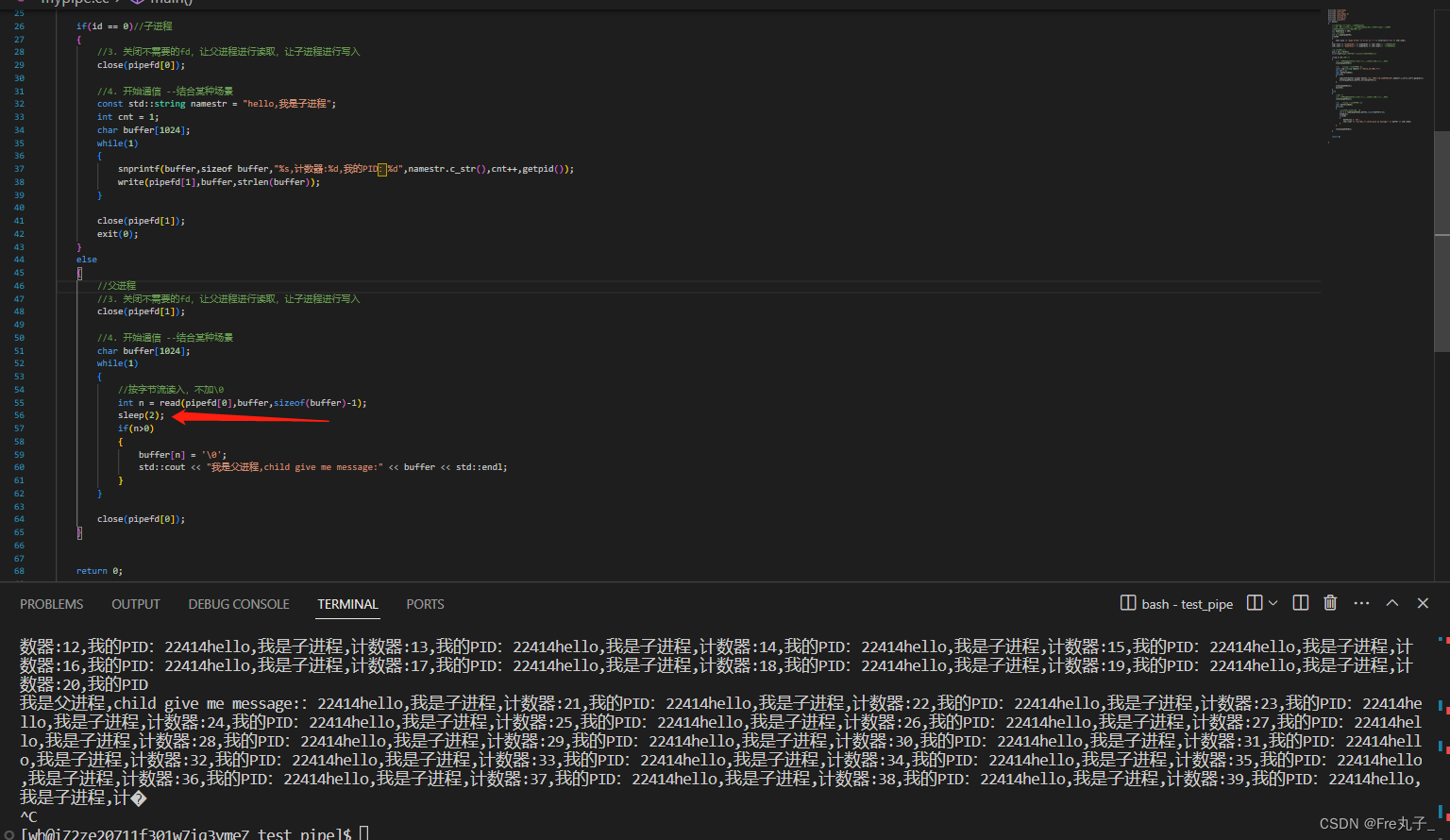
匿名管道的退出
因为当管道的读端关闭后,写端也会随之关闭,当我们让父进程进程读,子进程进行写时,我们关闭写端后,子进程是否会正常退出,我们来认识分析一下
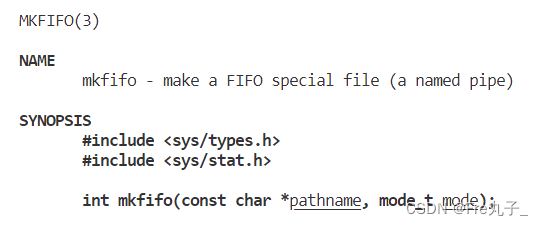
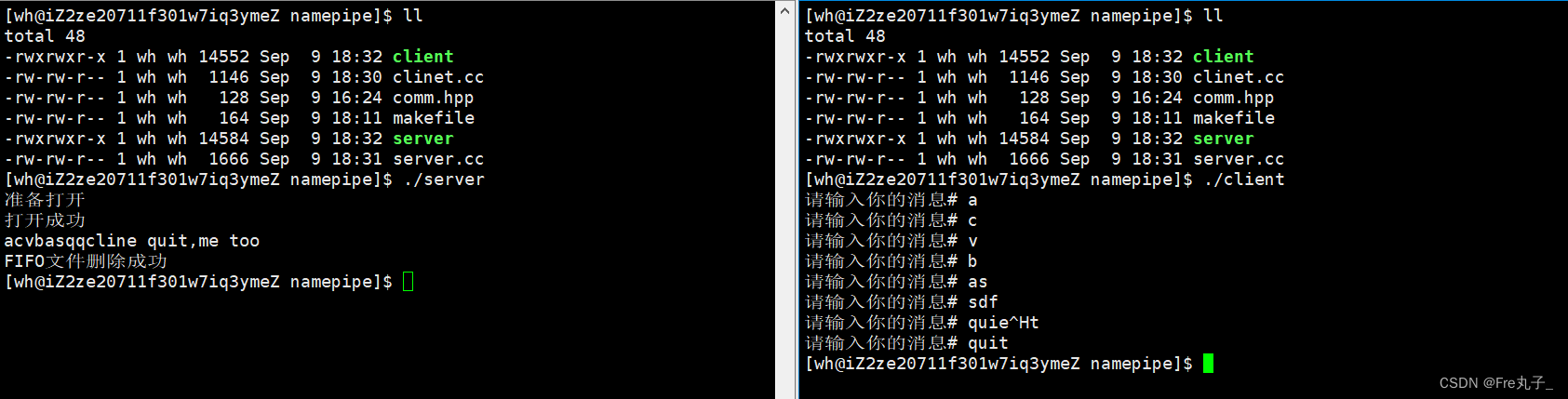
命名管道的退出
mkfifo用于创建一个FIFO(命名管道)文件。FIFO文件在使用后会保留在文件系统中,不会自动删除。
如果想要自动删除需要用到
unlink命令在调用unlink函数后,它会尝试删除指定的文件。如果成功删除文件,unlink将返回0,否则返回-1,并且此时可以通过errno变量获取错误信息。
相关文章:
【Linux】管道
管道命令 #include <unistd.h> int pipe(int pipefd[2]); 在Linux中,管道(pipe)的返回值是一个整数数组,包含两个文件描述符。这两个文件描述符分别代表管道的读端和写端。 当成功创建一个管道时,pipe() 系统调用…...
postgre 12.11单实例安装文档
一 下载 访问https://www.postgresql.org/download/,点击左侧的‘source进行下载,一般选择bz2的安装包。 二 安装 这里安装12.11版本的postgre,数据目录路径为/data/server/pgdata,端口为5432. 2.1 安装依赖包 #安装 yum in…...

使用LightPicture开源搭建私人图床:详细教程及远程访问配置方法
文章目录 1.前言2. Lightpicture网站搭建2.1. Lightpicture下载和安装2.2. Lightpicture网页测试2.3.cpolar的安装和注册 3.本地网页发布3.1.Cpolar云端设置3.2.Cpolar本地设置 4.公网访问测试5.结语 1.前言 现在的手机越来越先进,功能也越来越多,而手机…...
:最初的项目思路(SLAM))
基于视觉重定位的室内AR导航项目思路(1):最初的项目思路(SLAM)
文章目录 最初的项目思路(SLAM):后文: 前情提要: 是第一次做项目的小白,文章内的资料介绍如有错误,请多包含! 最初的项目思路(SLAM): 由于我们在…...
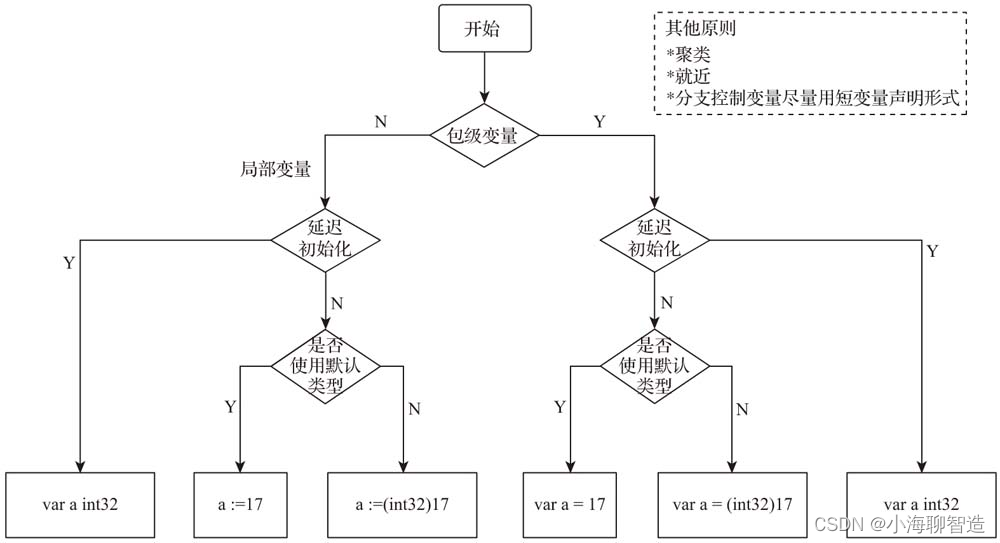
小白学go基础05-变量声明形式
和Python、Ruby等动态脚本语言不同,Go语言沿袭了静态编译型语言的传统:使用变量之前需要先进行变量的声明。 变量声明形式使用决策流程图 这里大致列一下Go语言常见的变量声明形式: var a int32 var s string "hello" var i 13 …...

高可用Kuberbetes部署Prometheus + Grafana
概述 阅读官方文档部署部署Prometheus Grafana GitHub - prometheus-operator/kube-prometheus at release-0.10 环境 步骤 下周官方github仓库 git clone https://github.com/prometheus-operator/kube-prometheus.git git checkout release-0.10 进入工作目录 cd kube…...
ardupilot 安装gcc-arm-none-eabi编译工具
目录 文章目录 目录摘要0简介1.下载网站2.安装摘要 本节主要记录ardupilot使用的编译器安装过程。 0简介 gcc-arm-none-eabi是GNU项目下的软件,是一个面向裸机arm的编译器。那么说了这么多介绍,它都包含什么具体功能又怎么安装与使用呢,我们继续。 1.下载网站 gcc-arm-n…...

ORACLE集群管理-19C RAC重新配置IPV6
1 问题概述 数据库已经配置和IPV6和 IPV4双线协议,需要重新配置IPV6 2 关闭相关资源 1 root用户执行 ./srvctl stop scan_listener -i 1 ./srvctl stop scan ./srvctl stop listener -n orcldb1 ./srvctl stop listener -n orcldb2 ./srvctl stop vip -n orcldb…...
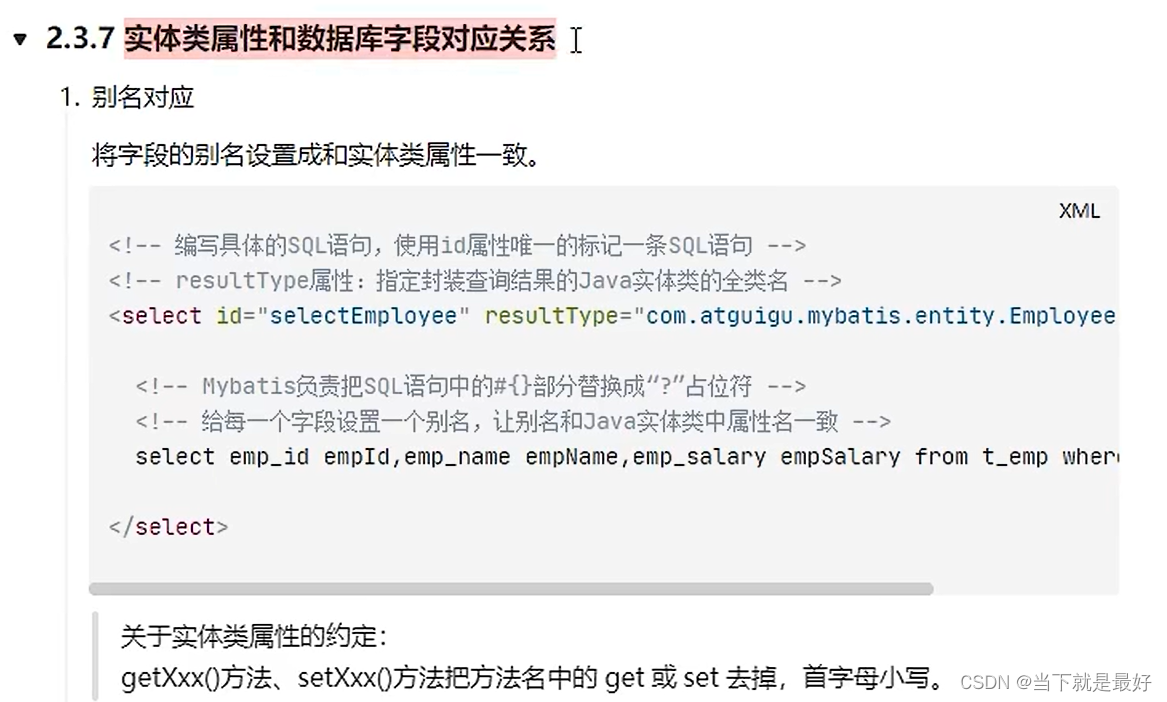
Mybatis实体类属性与数据库字段的对应关系
方法一:起别名 select t_id(数据库字段) tId(类的属性), ... , ...from 表名 方法二:开启驼峰映射 <!-- 开启驼峰映射 数据库 s_id java类 sId--><setting name"mapUnderscoreToCamelCase" value"true"/> 当java类中属性命名…...

Unity(三) Shader着色器初探
学习3D开发技术的时候无可避免的要接触到Shader,那么Shader是个什么概念呢?其实对于开发同事来说还是比较难理解的,一般来说Shader是服务于图形渲染的一类技术,开发人员可以通过其shader语言来自定义显卡渲染页面的算法࿰…...
苹果电脑要安装杀毒软件吗?mac用什么杀毒软件好?
对于这个问题让人很是纠结,Mac不需要杀毒这个理论一直都深入人心,Mac OS X权限管理特性可以防毒的说法也一直甚嚣尘上,很多小伙伴如我一样搞不清楚到底要不要安装杀毒软件。,毕竟当前个人信息安全泄露泛滥不穷的年代,我…...

MySQL——索引
索引在 MySQL 数据库中分三类: B 树索引Hash 索引全文索引 目的:在查询的时候提升效率 b树 参考:https://blog.csdn.net/qq_40649503/article/details/115799935 数据库索引,是数据库管理系统中一个排序的数据结构…...

110. 平衡二叉树
题目链接: 力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 递归法: 我的代码: *** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* Tree…...
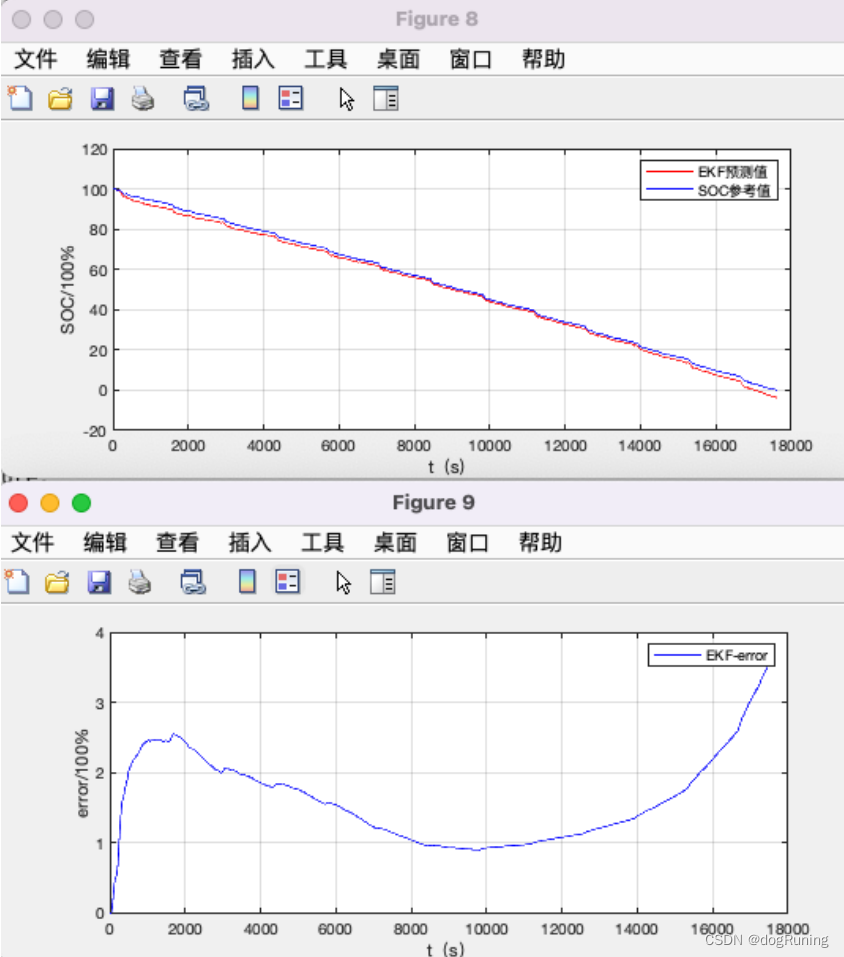
遗忘因子递推最小二乘参数估计(FFRLS)
基于遗忘因子的最小二乘法电池参数辨识 最小二乘法是系统辨识中最常用的一种估算方法。为了克服最小二乘法存在”数据饱和”的问题,我们通常采用含有遗忘因子的递推最小二乘法(Forgetting Factor Recursive Least Square,FFRLS)算法进行电池模型的参数辨识。 1、二…...
【redis进阶】基础知识简要回顾
1. 常见功能介绍 聚合统计 使用list集合的差集、并集来统计 排序统计 SortedSet(ZSet)统计,再利用分页列出权重高的元素 二值状态统计 BitMap存储,获取并统计 SETBIT uid:sign:3000:202008 2 1 GETBIT uid:sign:3000:202008 2…...
HTML5-3-表格
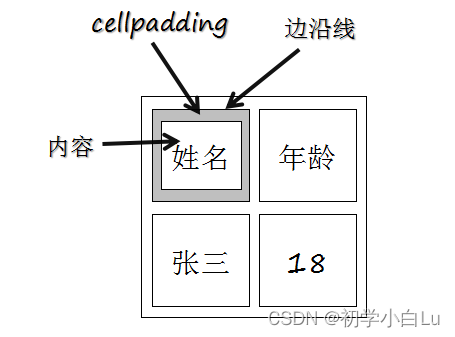
文章目录 属性边框属性标题跨行和跨列单元格边距 HTML 表格由 <table> 标签来定义。 tr:tr 是 table row 的缩写,表示表格的一行。td:td 是 table data 的缩写,表示表格的数据单元格。th:th 是 table header的缩…...

Spring Boot + Vue的前后端项目结构及联调查询
Spring Boot Vue的前后端项目结构及联调查询 当你刚开始学习前后端开发时,可能会感到有些困惑和不知所措。下面是一些建议,希望能为你的学习之旅提供一些启示: 建立坚实的基础知识:学习前后端开发的第一步是建立坚实的基础知识。…...

Transformer貌似也是可以使用state递归解码和训练的
import paddle import numpy as npclass HeadLoss(paddle.nn.Layer):def __init__(self):super(HeadLoss, self).__init__()...

振弦采集仪应用地铁隧道安全监测详细解决方案
振弦采集仪应用地铁隧道安全监测详细解决方案 随着城市化进程的不断加快,地铁作为一种高效、便捷、环保的交通方式已经成为现代城市不可或缺的一部分。因此,对地铁的安全性也越来越重视,一般二三线以上的城市在不断发展中,地铁做…...
2023 IntelliJ IDEA下载、安装教程, 附详细图解
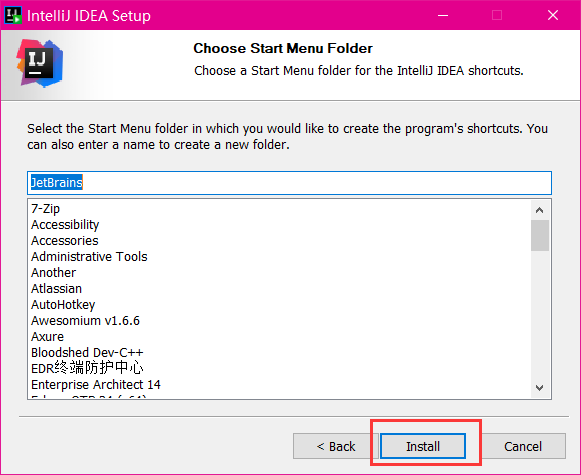
文章目录 下载与安装IDEA推荐阅读 下载与安装IDEA 首先先到官网下载最新版的IntelliJ IDEA, 下载后傻瓜式安装就好了 官网下载地址:https://www.jetbrains.com/ 1、下载完后在本地找到该文件,双击运行 idea 安装程序 2、点击 Next 3、选择安装路径&…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

前端导出带有合并单元格的列表
// 导出async function exportExcel(fileName "共识调整.xlsx") {// 所有数据const exportData await getAllMainData();// 表头内容let fitstTitleList [];const secondTitleList [];allColumns.value.forEach(column > {if (!column.children) {fitstTitleL…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

解决本地部署 SmolVLM2 大语言模型运行 flash-attn 报错
出现的问题 安装 flash-attn 会一直卡在 build 那一步或者运行报错 解决办法 是因为你安装的 flash-attn 版本没有对应上,所以报错,到 https://github.com/Dao-AILab/flash-attention/releases 下载对应版本,cu、torch、cp 的版本一定要对…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

图表类系列各种样式PPT模版分享
图标图表系列PPT模版,柱状图PPT模版,线状图PPT模版,折线图PPT模版,饼状图PPT模版,雷达图PPT模版,树状图PPT模版 图表类系列各种样式PPT模版分享:图表系列PPT模板https://pan.quark.cn/s/20d40aa…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

嵌入式常见 CPU 架构
架构类型架构厂商芯片厂商典型芯片特点与应用场景PICRISC (8/16 位)MicrochipMicrochipPIC16F877A、PIC18F4550简化指令集,单周期执行;低功耗、CIP 独立外设;用于家电、小电机控制、安防面板等嵌入式场景8051CISC (8 位)Intel(原始…...

WPF八大法则:告别模态窗口卡顿
⚙️ 核心问题:阻塞式模态窗口的缺陷 原始代码中ShowDialog()会阻塞UI线程,导致后续逻辑无法执行: var result modalWindow.ShowDialog(); // 线程阻塞 ProcessResult(result); // 必须等待窗口关闭根本问题:…...