[学习笔记]Node2Vec图神经网络论文精读
参考资料:https://www.bilibili.com/video/BV1BS4y1E7tf/?p=12&spm_id_from=pageDriver
Node2vec简述
DeepWalk的缺点
用完全随机游走,训练节点嵌入向量,仅能反应相邻节点的社群相似信息,无法反映节点的功能角色相似信息。
Node2vec
通过调节p和q的参数,可以调节权重。
p值很小,更愿意返回,则类似BFS,反映的是微观视角。
q值很小,更愿意返回,则类似DFS,反映宏观视角。
DFS捕捉的是homophily同质社群(社交网络)的特征
BFS捕捉的是Structural equivalence节点功能角色(中枢、桥接、边缘)的特征。
伪代码


一些技术细节
Alias Sampling:用空间换时间,时间复杂度O(1)的采样算法。
Node2vec论文精读
任何监督学习算法要求有内含丰富语义,有分类区分性以及相互独立的特征。
图嵌入的方法:
1.手动构造特征
2.基于矩阵分解的图嵌入
3.基于随机游走的图嵌入
4.基于神经网络
同一个社群的节点、同一个功能角色的节点,应该被编码成相近的embedding
使用二阶随机游走方法来产生节点的邻域。
一阶随机游走(一阶马尔科夫性):下一个节点仅与当前节点有关(deepwalk,pagerank)
二阶随机游走(二阶马尔科夫性):下一个节点不仅与当前节点有关,还与上一个节点有关
p,q的不同对应不同的探索策略,具有可解释性。
最优的p,q可以通过调惨得到。
贡献
1.提出node2vec,可以通过调节p、q来探索网络的不同特性,使用SGD来优化
2.node2vec符合网络科学的准则,提供了灵活的表示
3.node2vec将节点嵌入推广到了连接嵌入
4.在多类别分类任务和连接预测任务上进行了实验。
3.Node2vec算法
图: G = ( V , E ) G=(V,E) G=(V,E)
采样策略: S S S
节点 u u u的领域节点 N S ( u ) ⊂ V N_S(u) \subset V NS(u)⊂V
任务:学习映射 f : V → R d f: V \rightarrow \mathbb{R}^d f:V→Rd:d是词嵌入后的维度
目标函数:
max f ∑ u ∈ V log Pr ( N S ( u ) ∣ f ( u ) ) \max _f \sum_{u \in V} \log \operatorname{Pr}\left(N_S(u) \mid f(u)\right) fmaxu∈V∑logPr(NS(u)∣f(u))
为了简化问题,做出两个假设:
- 条件独立性假设:周围节点互相不影响:
Pr ( N S ( u ) ∣ f ( u ) ) = ∏ n i ∈ N S ( u ) Pr ( n i ∣ f ( u ) ) \operatorname{Pr}\left(N_S(u) \mid f(u)\right)=\prod_{n_i \in N_S(u)} \operatorname{Pr}\left(n_i \mid f(u)\right) Pr(NS(u)∣f(u))=ni∈NS(u)∏Pr(ni∣f(u)) - 特征空间的对称性:两个节点之间相互影响的程度是一样的,因此可以用特征的点乘来表示概率
Pr ( n i ∣ f ( u ) ) = exp ( f ( n i ) ⋅ f ( u ) ) ∑ v ∈ V exp ( f ( v ) ⋅ f ( u ) ) \operatorname{Pr}\left(n_i | f(u)\right)=\frac{\exp \left(f\left(n_i\right) \cdot f(u)\right)}{\sum_{v \in V} \exp (f(v) \cdot f(u))} Pr(ni∣f(u))=∑v∈Vexp(f(v)⋅f(u))exp(f(ni)⋅f(u))
设 Z u = ∑ v ∈ V exp ( f ( u ) ⋅ f ( v ) ) Z_u=\sum_{v \in V} \exp (f(u) \cdot f(v)) Zu=∑v∈Vexp(f(u)⋅f(v)),称为配分函数,则目标函数可化为
Pr ( n i ∣ f ( u ) ) = exp ( f ( n i ) ⋅ f ( u ) ) ∑ v ∈ V exp ( f ( v ) ⋅ f ( u ) ) \operatorname{Pr}\left(n_i \mid f(u)\right)=\frac{\exp \left(f\left(n_i\right) \cdot f(u)\right)}{\sum_{v \in V} \exp (f(v) \cdot f(u))} Pr(ni∣f(u))=∑v∈Vexp(f(v)⋅f(u))exp(f(ni)⋅f(u))
3.1 传统搜索策略
如何定义领域 N S ( u ) N_S(u) NS(u)依赖于策略 S S S。不同策略下,邻域是不一样的。
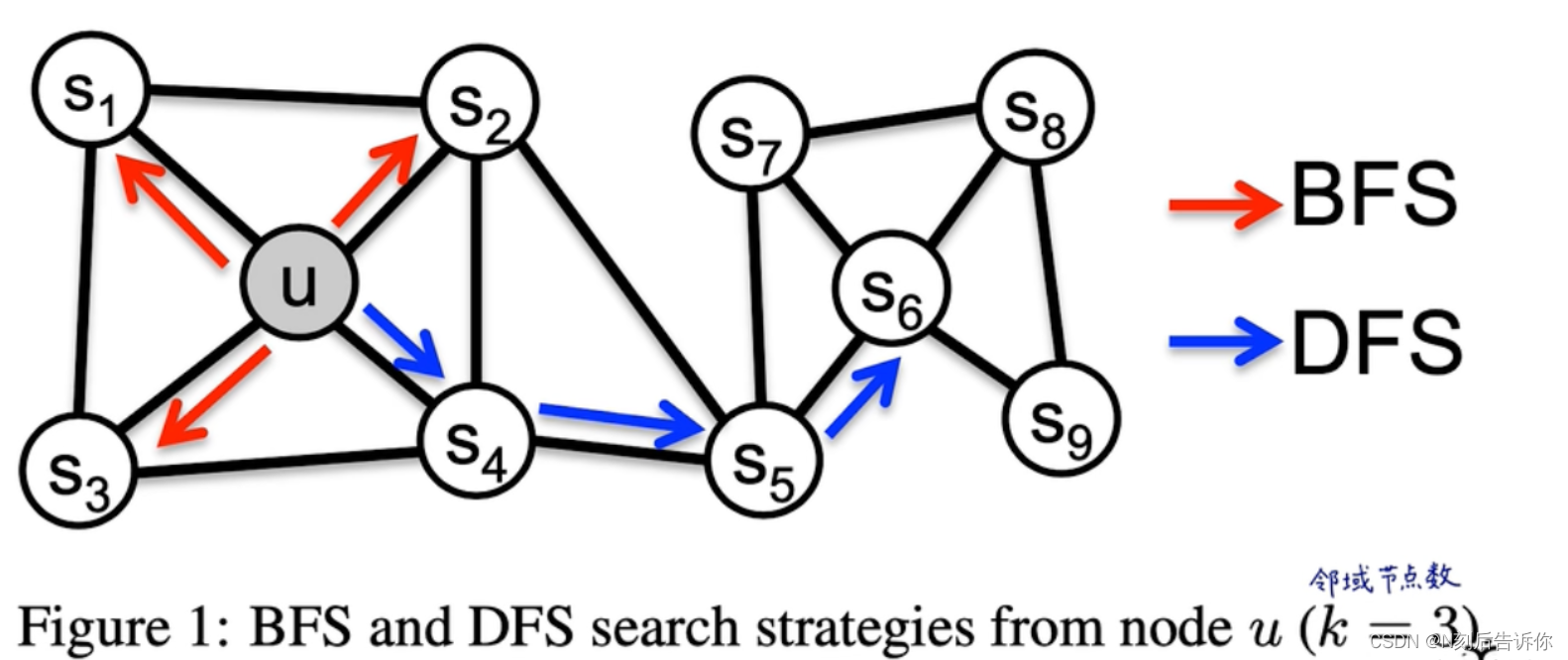
BFS:只探索近邻。
DFS:渐行渐远,探索离原节点较远的节点。
在homophily(同质性)假设下(对应BFS),同一个社区的节点,词嵌入后会比较相似。如s1和u
在structural equivalence假设下(对应DFS),有相同结构角色功能的节点,词嵌入后会比较相似。如u和s6
在真实图里,这两种不是互斥的,一个图可能既有homophily特质,也有structural equivalence特质。
BFS采样结果比较稳定,方差较小。
DFS采样结果比较不稳定,方差较大。
3.2 node2vec
3.2.1 随机游走
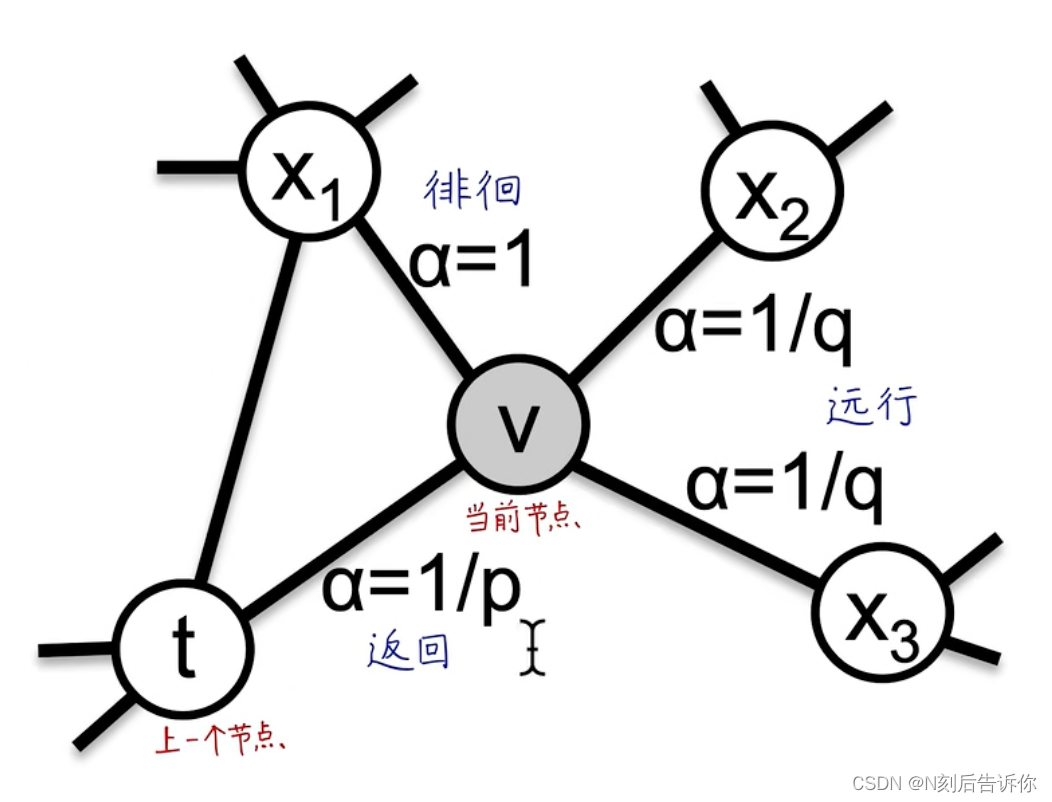
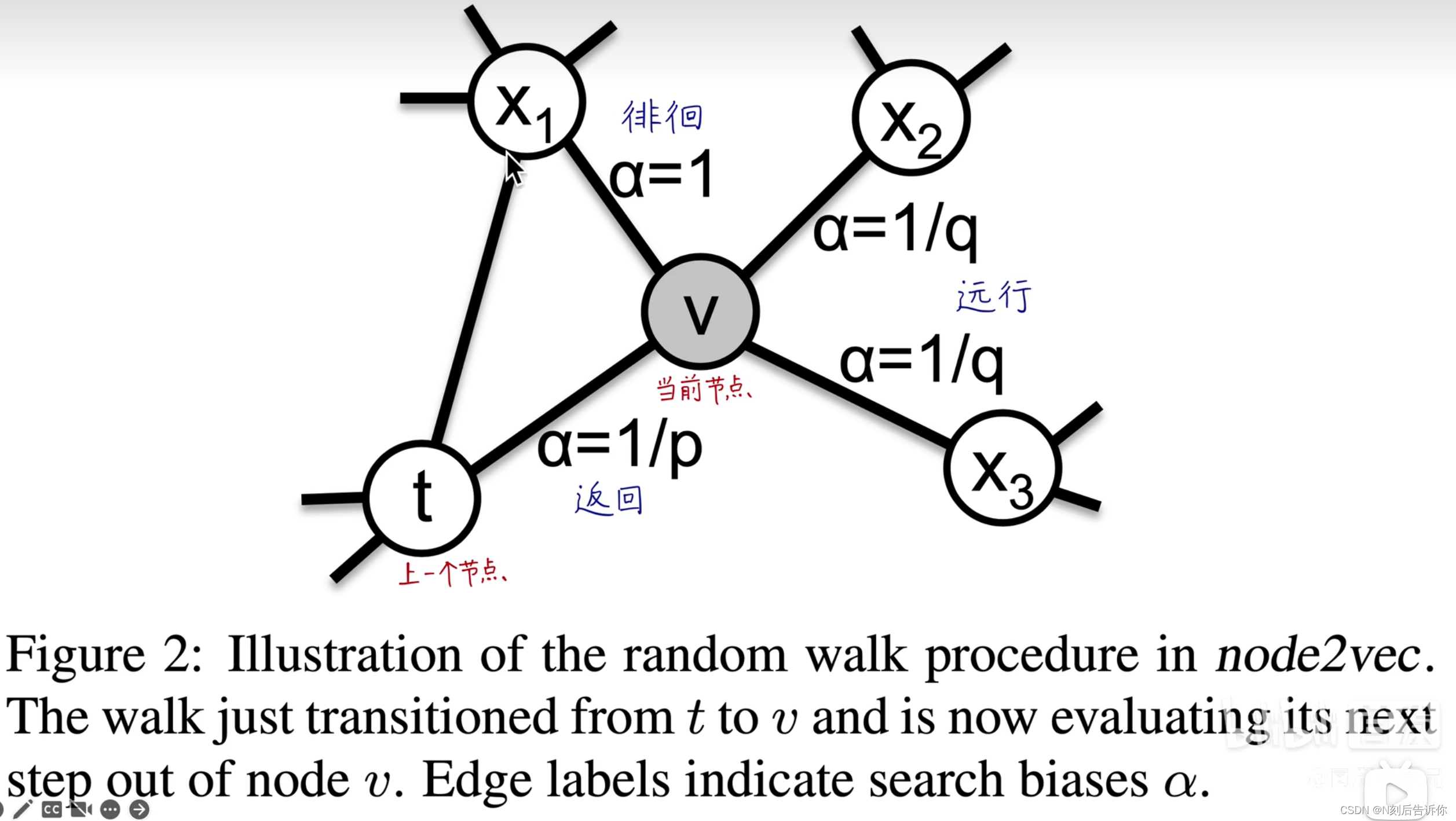
u u u:起始点
t t t:上一节点
v v v:当前节点
x x x:下一节点
N s ( t ) N_s(t) Ns(t):上一节点的邻居节点
k k k:当前节点v的邻居节点个数
l l l:随机游走序列节点个数
下一个节点的生成概率公式:
P ( c i = x ∣ c i − 1 = v ) = { π v x Z if ( v , x ) ∈ E 0 otherwise P\left(c_i=x \mid c_{i-1}=v\right)= \begin{cases}\frac{\pi_{v x}}{Z} & \text { if }(v, x) \in E \\ 0 & \text { otherwise }\end{cases} P(ci=x∣ci−1=v)={Zπvx0 if (v,x)∈E otherwise
其中, π v x \pi_{v x} πvx是未归一化的转移概率。
3.2.2 搜索的偏向 α \alpha α
直接用权重作为游走概率,则无法调节搜索策略。直接用BFS或者DFS则太极端,无法平滑调节。
于是考虑带参数p和q的二阶随机游走:
α p q ( t , x ) = { 1 p if d t x = 0 1 if d t x = 1 1 q if d t x = 2 \alpha_{p q}(t, x)= \begin{cases}\frac{1}{p} & \text { if } d_{t x}=0 \\ 1 & \text { if } d_{t x}=1 \\ \frac{1}{q} & \text { if } d_{t x}=2\end{cases} αpq(t,x)=⎩ ⎨ ⎧p11q1 if dtx=0 if dtx=1 if dtx=2
π v x = α p q ( t , x ) ⋅ w v x \pi_{v x}=\alpha_{p q}(t, x) \cdot w_{v x} πvx=αpq(t,x)⋅wvx
因为既要下一个节点x考虑当前节点v可达,也要考虑x与上一个节点t的距离,所以是二阶的随机游走
空间复杂度:随机游走需要存邻接表 O ( ∣ E ∣ ) O(|E|) O(∣E∣)。为了方便,二阶随机游走需要存 O ( a 2 ∣ V ∣ ) O(a^2|V|) O(a2∣V∣)来记录距离,其中 a a a是图中每个点的平均连接数。
时间复杂度: O ( l k ( l − k ) ) O\left(\frac{l}{k(l-k)}\right) O(k(l−k)l),k是领域的节点个数
随着硬件的发展,空间复杂度没有时间复杂度重要
3.2.3 伪代码

总共分为三个阶段:
- 已知p,q和图权重,生成随机游走的采样策略,存入表中
- 每个节点生成r个随机游走序列,其中node2vecWalk函数用于生成起始点为u,长为l的随机游走序列。

- 用生成的随机游走序列,通过skip-gram模型训练得到节点嵌入表示
AliasSampling是用空间(预处理)换时间的方法,它的时间复杂度是O(1),特别适用于大量反复抽样情况下,优势很突出。它将离散分布抽样转换为均匀分布抽样。
随机游走过程中,会有隐式的偏差。所以每个节点都采样r次,尽可能减少偏差。
每个阶段都可以并行,并且可以异步训练,可扩展性非常好
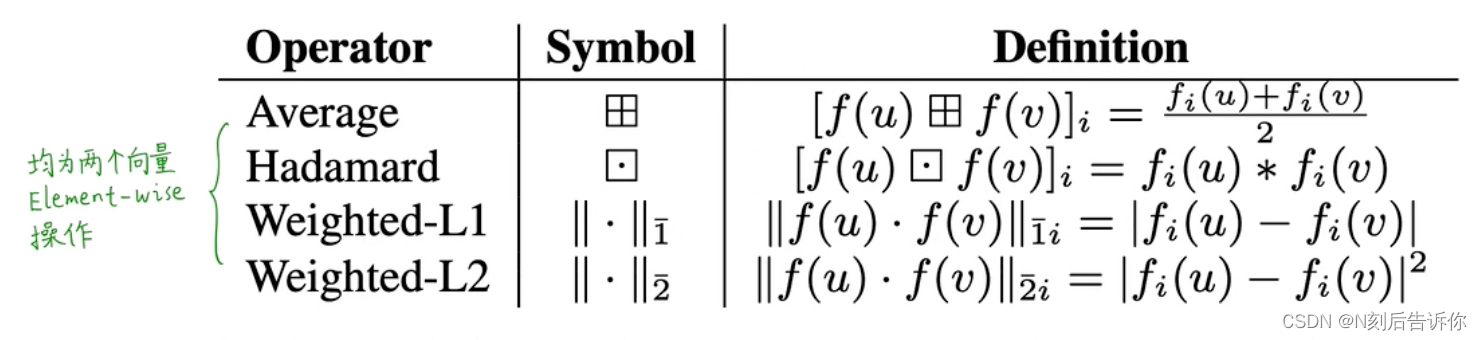
3.3 学习连接的特征
将node embedding扩展到link embedding
给定两个节点,定义一个二元操作符 ∘ \circ ∘来生成连接的表示:
4.实验
4.1:悲惨世界人物关系图的图嵌入
4.2 实验设置
与其他算法对比
严格控制各对比实验的条件
4.3 多标签分类
4.4 参数敏感度
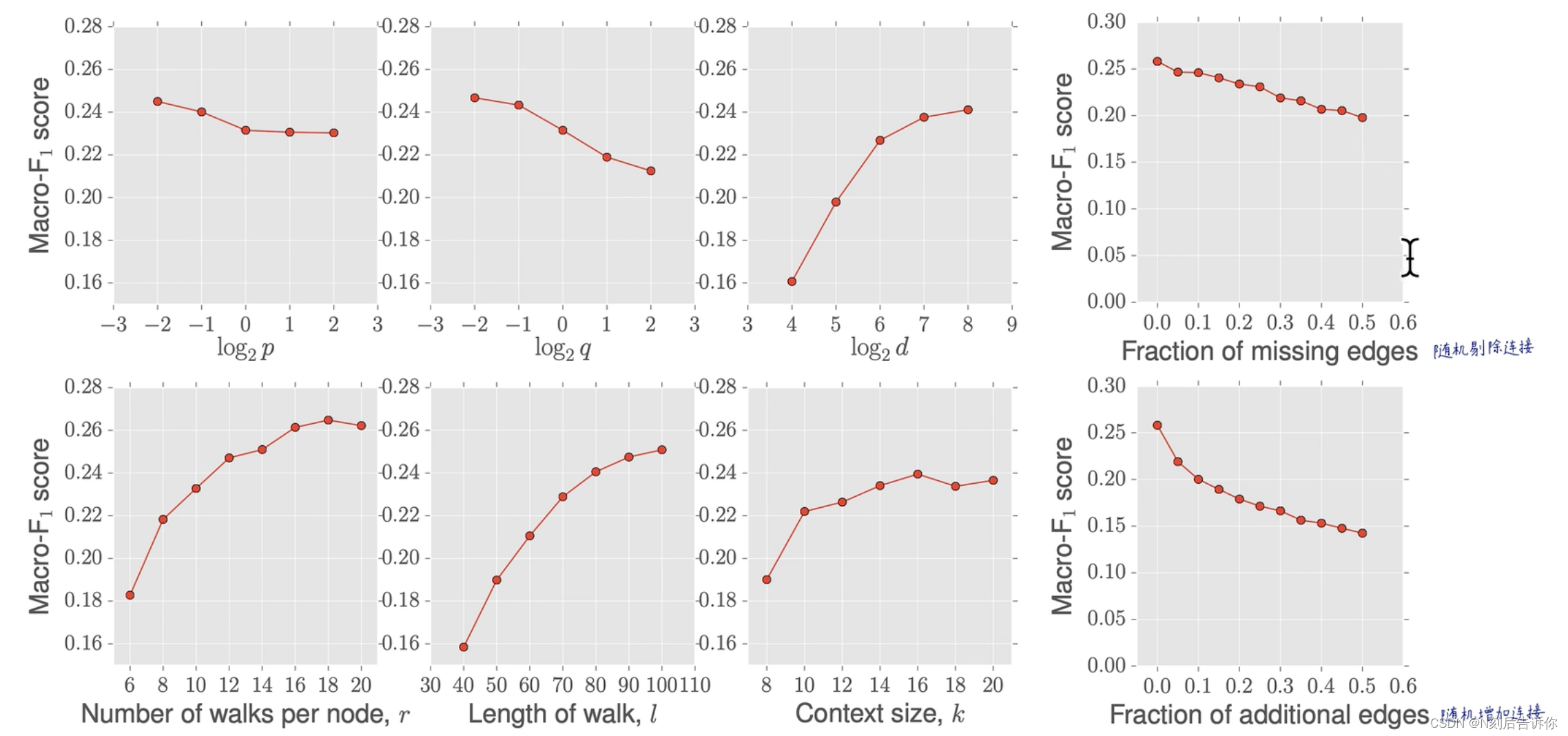
随机剔除一些连接,性能会缓慢下降
4.5 扰动分析
缺失连接:保证连通域不变的情况下,进行剪枝,不会造成新的孤岛。
噪声增加连接:随机增加连接,在传感器网络中更常见。
4.6 可扩展性
构建E-R随机图,节点数从100到100万,来做node2vec算法,来看时间。可以看到时间复杂度近似为线性。
4.7 连接预测
构建正负样本的二分类问题。
采集测试集:从网络中取50%的边,同时确保不改变剩下的网络的连通性。再从网络中随机选取一些不相邻的节点对,作为负样本。然后可以训练二分类模型了。
5.讨论和结论
node2vec展示了一定的可解释性,p、q参数是灵活可调的,在复杂任务上的性能不错,特别是在扰动数据集上。
节点嵌入可以拓展到连接嵌入上。
相关文章:

[学习笔记]Node2Vec图神经网络论文精读
参考资料:https://www.bilibili.com/video/BV1BS4y1E7tf/?p12&spm_id_frompageDriver Node2vec简述 DeepWalk的缺点 用完全随机游走,训练节点嵌入向量,仅能反应相邻节点的社群相似信息,无法反映节点的功能角色相似信息。 …...

C# Linq源码分析之Take(五)
概要 本文在C# Linq源码分析之Take(四)的基础上继续从源码角度分析Take的优化方法,主要分析Where.Select.Take的使用案例。 Where.Select.Take的案例分析 该场景模拟我们显示中将EF中与数据库关联的对象进行过滤,然后转换成Web…...
性能监控-grafana+prometheus+node_exporter
Prometheus是一个开源的系统监控和报警工具。它由SoundCloud开发并于2012年发布,后来成为了一个独立的开源项目,并得到了广泛的应用和支持。 Prometheus的主要功能包括采集和存储各种系统和应用程序的监控数据,并提供强大的查询语言PromQL来…...
(STM32H5系列)STM32H573RIT6、STM32H573RIV6、STM32H573ZIT6嵌入式微控制器基于Cortex®-M33内核
一、应用 工业(PLC、工业电机控制、泵和压缩机) 智能家居(空调、冰箱、冰柜、中央警报系统、洗衣机) 个人电子产品(键盘、智能手机、物联网标签、跟踪设备) 智能城市(工业通信、照明控制、数字…...

mysql配置bind-address不生效
1、前言 因为要ip直接访问mysql,故去修改bind-address参数,按照mysql配置文件查找顺序是:/etc/my.cnf、/etc/mysql/my.cnf、~/.my.cnf,服务器上没有 /etc/my.cnf文件,故去修改 /etc/mysql/my.cnf文件,但是一…...

Linux相关指令(下)
cat指令 查看目标文件的内容 常用选项: -b 对非空输出行编号 -n 对输出的所有行编号 -s 不输出多行空行 一个重要思想:linux下一切皆文件,如显示器文件,键盘文件 cat默认从键盘中读取数据再打印 退出可以ctrlc 输入重定向<…...
(A - F))
Codeforces Round 855 (Div 3)(A - F)
Codeforces Round 855 (Div. 3)(A - F) Codeforces Round 855 (Div. 3) A. Is It a Cat?(思维) 思路:先把所有字母变成小写方便判断 , 然后把每一部分取一个字母出来 , 判断和‘meow’是否相同即可。 复杂度 O ( n…...
:社交媒体金融的未来,真的如此美好吗?)
Friend.tech(FT):社交媒体金融的未来,真的如此美好吗?
Friend.tech(FT)是一个在2023年8月10日正式推出的社交金融平台,它的特点在于允许用户购买和出售创作者的股票(shares),这些股票赋予用户访问创作者内容的权利。FT的推出引发了广泛的关注,吸引了…...
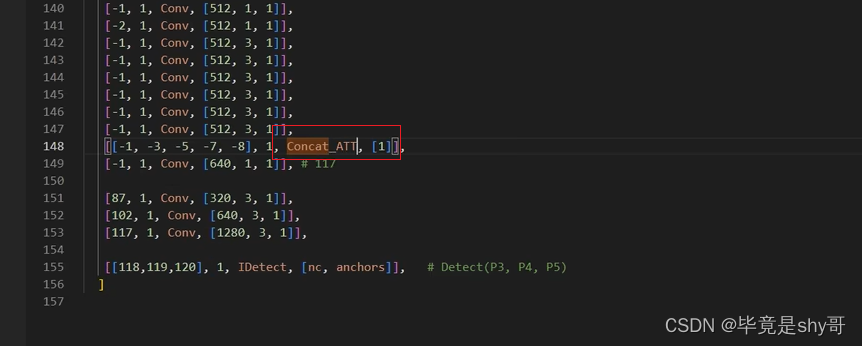
yolov7中Concat之后加注意力模块(最复杂的情况)
1、common.py中找到Concat模块,复制一份 2、要传参进来,dim通道数 3、然后找yolo.py模块,添加 4、yaml里替换 5、和加的位置也有关系...
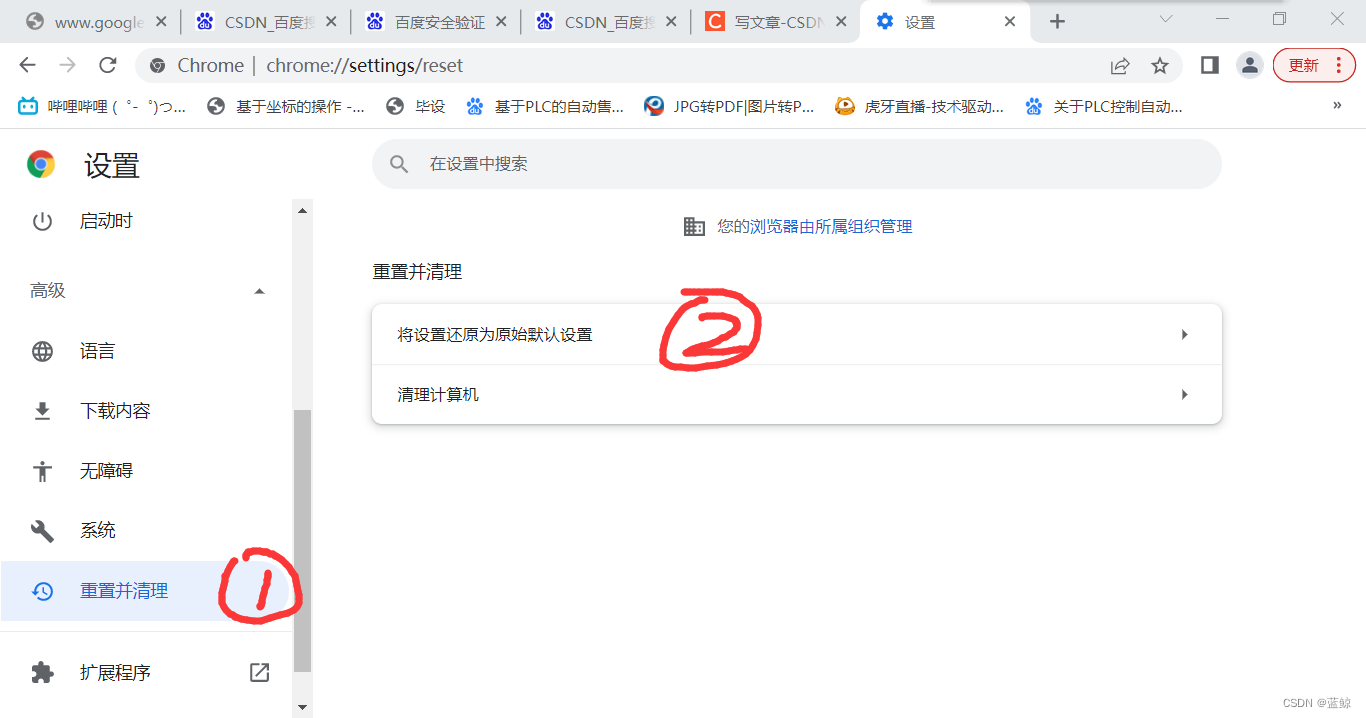
解除百度安全验证
使用chrome浏览器用百度浏览时,一直弹百度安全验证: 在设置里进行重置: 然后重启浏览器就可以了。...
(A - F))
Codeforces Round 731 (Div 3)(A - F)
Codeforces Round 731 (Div. 3)(A - F) Dashboard - Codeforces Round 731 (Div. 3) - Codeforces A. Shortest Path with Obstacle(思维) 思路:显然要计算 A → B 之间的曼哈顿距离 , 要绕开 F 当且仅当 AB形成的直线平行于坐…...
与sorted()函数详解)
Python的sort()与sorted()函数详解
目录 sort()函数 sorted()函数 key参数 区别 sort()函数 sort()方法:该方法用于原地对列表进行排序,即直接在原始列表上进行排序操作,并不返回一个新的列表。 my_l…...

用python实现基本数据结构【04/4】
说明 如果需要用到这些知识却没有掌握,则会让人感到沮丧,也可能导致面试被拒。无论是花几天时间“突击”,还是利用零碎的时间持续学习,在数据结构上下点功夫都是值得的。那么Python 中有哪些数据结构呢?列表、字典、集…...

“必抓!”算法
一个程序员一生中可能会邂逅各种各样的算法,但总有那么几种,是作为一个程序员一定会遇见且大概率需要掌握的算法。今天就来聊聊这些十分重要的“必抓!”算法吧~ 你可以从以下几个方面进行创作(仅供参考) 一ÿ…...

【监控系统】Promethus整合Alertmanager监控告警邮件通知
【监控系统】Promethus整合Alertmanager监控告警邮件通知 Alertmanager是一种开源软件,用于管理和报警监视警报。它与Prometheus紧密集成,后者是一种流行的开源监视和警报系统。Alertmanager从多个源接收警报和通知,并根据一组配置规则来决定…...
【韩顺平】Linux基础
目录 1.网络连接三种方式 1.1 桥接模式:虚拟系统可以和外部系统通讯,但是容易造成IP冲突【1-225】 1.2 NAT模式:网络地址转换模式。虚拟系统可以和外部系统通讯,不造成IP冲突。 1.3 主机模式:独立的系统。 2.虚拟机…...

好奇一下各个大模型对华为mate60系列的看法
目前华为Mate60系列手机已上市并获抢购,个人觉得很不错,很好奇各个AI大模型对此事的看法,于是对chatGPT、文心一言、讯飞星火进行了一下粗浅的测试。 题目一(看看三个模型的综合分析能力) “目前华为Mate60系列手机已…...

UMA 2 - Unity Multipurpose Avatar☀️五.如何使用别人的Recipe和创建自己的服饰Recipe
文章目录 🟥 使用别人的Recipe1️⃣ 导入UMA资源效果展示2️⃣ 更新Library3️⃣ 试一下吧🟧 创建自己的服饰Recipe1️⃣ 创建自己的服饰Recipe2️⃣ 选择应用到的Base Recipe3️⃣ 指定显示名 / 佩戴位置 / 隐藏部位4️⃣ 给该服饰Recipe指定Slot / Overlay🚩 赋予Slot�…...

代码随想录训练营第五十六天| 583. 两个字符串的删除操作 、72. 编辑距离
583. 两个字符串的删除操作 题目链接/文章讲解/视频讲解:代码随想录 1.代码展示 //583.两个字符串的删除操作 int minDistance(string word1, string word2) {//step1 构建dp数组,dp[i][j]的含义是要使以i-1为结尾的word1和以j-1为结尾的word2//删除其元…...

hive解决了什么问题
hive出现的原因 Hive 出现的原因主要有以下几个: 传统数据仓库无法处理大规模数据:传统的数据仓库通常采用关系型数据库作为底层存储,这种数据库在处理大规模数据时效率较低。MapReduce 难以使用:MapReduce 是一种分布式计算框架…...

为什么需要建设工程项目管理?工程项目管理有哪些亮点功能?
在建筑行业,项目管理的重要性不言而喻。随着工程规模的扩大、技术复杂度的提升,传统的管理模式已经难以满足现代工程的需求。过去,许多企业依赖手工记录、口头沟通和分散的信息管理,导致效率低下、成本失控、风险频发。例如&#…...

Auto-Coder使用GPT-4o完成:在用TabPFN这个模型构建一个预测未来3天涨跌的分类任务
通过akshare库,获取股票数据,并生成TabPFN这个模型 可以识别、处理的格式,写一个完整的预处理示例,并构建一个预测未来 3 天股价涨跌的分类任务 用TabPFN这个模型构建一个预测未来 3 天股价涨跌的分类任务,进行预测并输…...

学习STC51单片机31(芯片为STC89C52RCRC)OLED显示屏1
每日一言 生活的美好,总是藏在那些你咬牙坚持的日子里。 硬件:OLED 以后要用到OLED的时候找到这个文件 OLED的设备地址 SSD1306"SSD" 是品牌缩写,"1306" 是产品编号。 驱动 OLED 屏幕的 IIC 总线数据传输格式 示意图 …...

实现弹窗随键盘上移居中
实现弹窗随键盘上移的核心思路 在Android中,可以通过监听键盘的显示和隐藏事件,动态调整弹窗的位置。关键点在于获取键盘高度,并计算剩余屏幕空间以重新定位弹窗。 // 在Activity或Fragment中设置键盘监听 val rootView findViewById<V…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...

Git常用命令完全指南:从入门到精通
Git常用命令完全指南:从入门到精通 一、基础配置命令 1. 用户信息配置 # 设置全局用户名 git config --global user.name "你的名字"# 设置全局邮箱 git config --global user.email "你的邮箱example.com"# 查看所有配置 git config --list…...

c++第七天 继承与派生2
这一篇文章主要内容是 派生类构造函数与析构函数 在派生类中重写基类成员 以及多继承 第一部分:派生类构造函数与析构函数 当创建一个派生类对象时,基类成员是如何初始化的? 1.当派生类对象创建的时候,基类成员的初始化顺序 …...

给网站添加live2d看板娘
给网站添加live2d看板娘 参考文献: stevenjoezhang/live2d-widget: 把萌萌哒的看板娘抱回家 (ノ≧∇≦)ノ | Live2D widget for web platformEikanya/Live2d-model: Live2d model collectionzenghongtu/live2d-model-assets 前言 网站环境如下,文章也主…...

数据结构:递归的种类(Types of Recursion)
目录 尾递归(Tail Recursion) 什么是 Loop(循环)? 复杂度分析 头递归(Head Recursion) 树形递归(Tree Recursion) 线性递归(Linear Recursion)…...