微调 TrOCR – 训练 TrOCR 识别弯曲文本
TrOCR（基于 Transformer 的光学字符识别）模型是性能最佳的 OCR 模型之一。在我们之前的文章中，我们分析了它们在单行打印和手写文本上的表现。然而，与任何其他深度学习模型一样，它们也有其局限性。TrOCR 在处理开箱即用的弯曲文本时表现不佳。本文将通过在弯曲文本数据集上微调 TrOCR 模型，使 TrOCR 系列更进一步。
图 1. 微调 TrOCR
从上一篇文章中我们知道TrOCR无法识别弯曲和垂直图像上的文本。这些图像是 SCUT-CTW1500 数据集的一部分。我们将在此数据集上训练 TrOCR 模型，并再次运行推理来分析结果。这将使我们全面了解针对不同用例可以将 TrOCR 模型的边界拓展到什么程度。
我们将使用 Hugging Face Trainer API 来训练模型。要完成整个过程，必须遵循以下步骤：
相关文章：
微调 TrOCR – 训练 TrOCR 识别弯曲文本
TrOCR（基于 Transformer 的光学字符识别）模型是性能最佳的 OCR 模型之一。在我们之前的文章中，我们分析了它们在单行打印和手写文本上的表现。然而，与任何其他深度学习模型一样，它们也有其局限性。TrOCR 在处理开箱即用的弯曲文本时表现不佳。本文将通过在弯曲文本数据集上…...
Jetsonnano B01 笔记7：Mediapipe与人脸手势识别
今日继续我的Jetsonnano学习之路，今日学习安装使用的是：MediaPipe 一款开源的多媒体机器学习模型应用框架。可在移动设备、工作站和服务 器上跨平台运行，并支持移动 GPU 加速。 介绍与程序搬运官方，只是自己的学习记录笔记&am…...
vue学习之v-if/v-else/v-else-if
v-else/v-else-if 创建 demo7.html,内容如下 <!DOCTYPE html> <html lang"en"><head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>Docum…...
ansible的安装和简单的块使用
目录 一、概述 二、安装 1、选择源 2、安装ansible 3、模块查看 三、实验 1、拓扑编辑 2、设置组、ping模块 3、hostname模块 4、file模块 编辑 5、stat模块 6、copy模块（本地拷贝到远程） 7、fetch模块与copy模块类似，但作用…...
Android 状态栏显示运营商名称
Android 原生设计中在锁屏界面会显示运营商名称，用户界面中，大概是基于 icon 数量长度显示考虑，对运营商名称不作显示。但是国内基本都加上运营商名称。对图标显示长度优化基本都是：缩小运营商字体、限制字数长度、信号图标压缩上…...
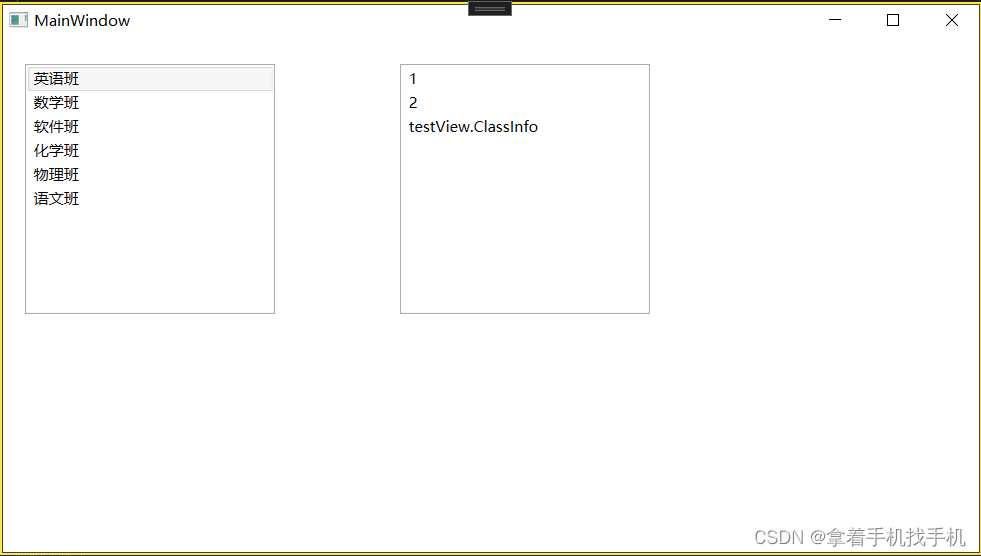
10.Xaml ListBox控件
1.运行界面 2.运行源码 a.Xaml 源码 <Grid Name="Grid1"><!--IsSelected="True" 表示选中--><ListBox x:Name="listBo...
基于vue3和element-plus的省市区级联组件
git地址：https://github.com/ht-sauce/elui-china-area-dht 使用:npm i elui-china-area-dht 默认使用 使用方法 <template><div class"app"><!--默认使用--><elui-china-area-dht change"onChange"></elui-china…...
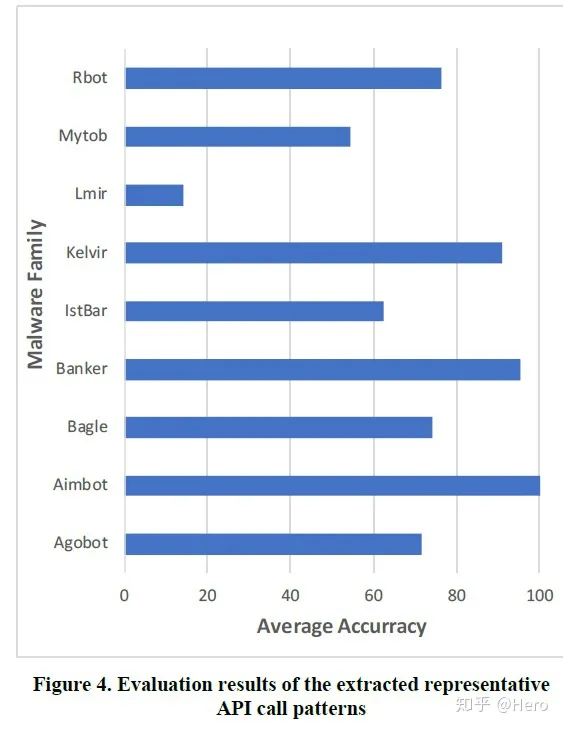
Paper: 利用RNN来提取恶意软件家族的API调用模式
论文 摘要 恶意软件家族分类是预测恶意软件特征的好方法，因为属于同一家族的恶意软件往往有相似的行为特征恶意软件检测或分类方法分静态分析和动态分析两种： 静态分析基于恶意软件中包含的特定签名进行分析，优点是分析的范围覆盖了整个代码…...
sdkman 安装以及 graalvm安装
sdkman安装以及graalvm安装全过程, (可能需要梯子) tiamTiam-Lenovo:~$ curl -s "https://get.sdkman.io" | bash-syyyyyyys:/yho: -yd./yh/ m..oho. hy ..sh/ :N -/…...
如何正确使用 WEB 接口的 HTTP 状态码和业务状态码？
当设计和开发 Web 接口时，必然会和 HTTP 状态码与业务状态码这两个概念打交道。很多同学可能没有注意过这两个概念或者两者的区别，做得稀里糊涂，接下来详细讲解下二者的定义、区别和使用方法。 HTTP 状态码 HTTP 状态码是由 HTTP 协议定义的…...
Spark【Spark SQL（三）DataSet】
DataSet DataFrame 的出现，让 Spark 可以更好地处理结构化数据的计算，但存在一个问题：编译时的类型安全问题，为了解决它，Spark 引入了 DataSet API（DataFrame API 的扩展）。DataSet 是分布式的数…...
制作立体图像实用软件：3DMasterKit 10.7 Crack
3DMasterKit 软件专为创建具有逼真 3D 和运动效果的光栅图片而设计：翻转、动画、变形和缩放。 打印机、广告工作室、摄影工作室和摄影师将发现 3DMasterKit 是一种有用且经济高效的解决方案，可将其业务扩展到新的维度，提高生成的 3D 图像和光…...
高校 Web 站点网络安全面临的主要的威胁
校园网 Web 站点的主要安全威胁来源于计算机病毒、内部用户恶意攻击和 破坏、内部用户非恶意的错误操作和网络黑客入侵等。 2.1 计算机病毒 计算机病毒是指编制者在计算机程序中插入的破坏计算机功能或者数据， 影响计算机使用并且能够自我复制的一组计算机指令或…...
vue前端解决跨域
1,首先 axios请求，看后端接口路径，http://122.226.146.110:25002/api/xx/ResxxList，所以baseURL地址改成 ‘/api’ let setAxios originAxios.create({baseURL: /api, //这里要改掉timeout: 20000 // request timeout}); export default s…...
【Cicadaplayer】解码线程及队列实现
4.4分支https://github.com/alibaba/CicadaPlayer/blob/release/0.4.4/framework/codec/ActiveDecoder.h对外：送入多个包，获取一个帧 int send_packet(std::unique_ptr<IAFPacket> &packet, uint64_t timeOut) override;int getFrame(std::u...
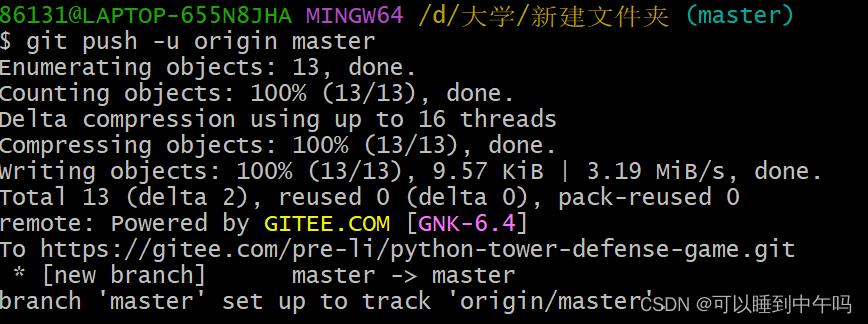
把文件上传到Gitee的详细步骤
目录 第一步：创建一个空仓库 第二步：找到你想上传的文件所在的地址，打开命令窗口，git init 第三步：git add 想上传的文件 ，git commit -m "给这次提交取个名字" 第四步：和咱们在第…...
基于keras中Lenet对于mnist的处理
文章目录 MNIST导入必要的包加载数据可视化数据集查看数据集的分布开始训练画出loss图画出accuracy图 使用数据外的图来测试图片可视化转化灰度图的可视化可视化卷积层的特征图第一层卷积 conv1 和 pool1第二层卷积 conv2 和 pool2 MNIST MNIST（Modified National …...
Python爬虫 教程：IP池的使用
前言 嗨喽~大家好呀，这里是魔王呐 ❤ ~! python更多源码/资料/解答/教程等 点击此处跳转文末名片免费获取 一、简介 爬虫中为什么需要使用代理 一些网站会有相应的反爬虫措施，例如很多网站会检测某一段时间某个IP的访问次数，如果访问频率…...
Ansible之playbook剧本
一、playbook概述1.1 playbook 介绍1.2 playbook 组成部分 二、playbook 示例2.1 playbook 启动及检测2.2 实例一2.3 vars 定义、引用变量2.4 指定远程主机sudo切换用户2.5 when条件判断2.6 迭代2.7 Templates 模块1.先准备一个以 .j2 为后缀的 template 模板文件，设…...
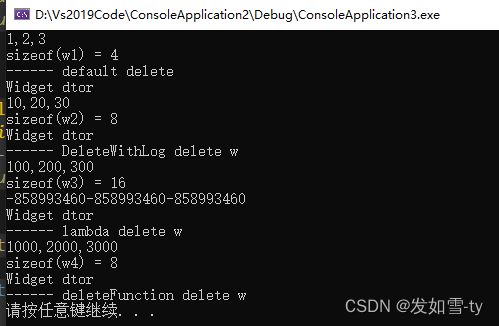
unique_ptr的大小探讨
unique_ptr大小和删除器有很大关系，具体区别看如下代码的分析。不要让unique_ptr占用的空间太大，否则不会达到裸指针同样的效果。 #include <iostream> #include <memory> using namespace std;class Widget {int m_x;int m_y;int m_z;publ…...
java 实现excel文件转pdf | 无水印 | 无限制
文章目录 目录 文章目录 前言 1.项目远程仓库配置 2.pom文件引入相关依赖 3.代码破解 二、Excel转PDF 1.代码实现 2.Aspose.License.xml 授权文件 总结 前言 java处理excel转pdf一直没找到什么好用的免费jar包工具，自己手写的难度，恐怕高级程序员花费一年的事件，也…...
docker 部署发现spring.profiles.active 问题
报错： org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...
Linux C语言网络编程详细入门教程：如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程：如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket（服务端和客户端都要）2. 绑定本地地址和端口&#x…...
云原生安全实战：API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填！ 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关（API Gateway） API网关是微服务架构中的核心组件，负责统一管理所有API的流量入口。它像一座…...
MySQL：分区的基本使用
目录 一、什么是分区二、有什么作用三、分类四、创建分区五、删除分区 一、什么是分区 MySQL 分区（Partitioning）是一种将单张表的数据逻辑上拆分成多个物理部分的技术。这些物理部分（分区）可以独立存储、管理和优化，…...
OD 算法题 B卷【正整数到Excel编号之间的转换】
文章目录 正整数到Excel编号之间的转换 正整数到Excel编号之间的转换 excel的列编号是这样的：a b c … z aa ab ac… az ba bb bc…yz za zb zc …zz aaa aab aac…; 分别代表以下的编号1 2 3 … 26 27 28 29… 52 53 54 55… 676 677 678 679 … 702 703 704 705;…...
MySQL的pymysql操作
本章是MySQL的最后一章，MySQL到此完结，下一站Hadoop！！！ 这章很简单，完整代码在最后，详细讲解之前python课程里面也有，感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...
麒麟系统使用-进行.NET开发
文章目录 前言一、搭建dotnet环境1.获取相关资源2.配置dotnet 二、使用dotnet三、其他说明总结 前言 麒麟系统的内核是基于linux的，如果需要进行.NET开发，则需要安装特定的应用。由于NET Framework 是仅适用于 Windows 版本的 .NET，所以要进…...
无需布线的革命：电力载波技术赋能楼宇自控系统-亚川科技
无需布线的革命：电力载波技术赋能楼宇自控系统 在楼宇自动化领域，传统控制系统依赖复杂的专用通信线路，不仅施工成本高昂，后期维护和扩展也极为不便。电力载波技术（PLC）的突破性应用，彻底改变了…...
c++算法学习3——深度优先搜索
一、深度优先搜索的核心概念 DFS算法是一种通过递归或栈实现的"一条路走到底"的搜索策略，其核心思想是： 深度优先：从起点出发，选择一个方向探索到底，直到无路可走 回溯机制：遇到死路时返回最近…...