基于物理层网络编码的相位同步算法matlab仿真
目录
1.算法运行效果图预览
2.算法运行软件版本
3.部分核心程序
4.算法理论概述
5.算法完整程序工程
1.算法运行效果图预览
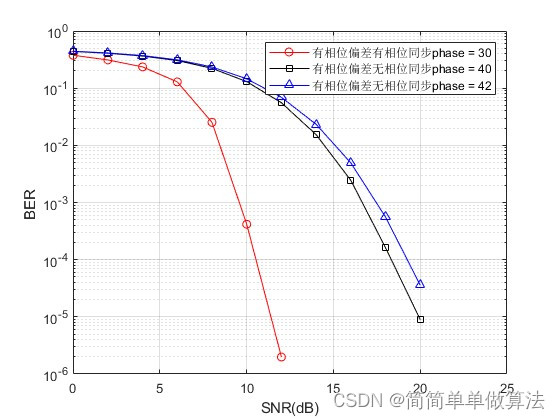
2.算法运行软件版本
matlab2022a
3.部分核心程序
..........................................................................%数据长度
Len = 504;
%网络数据包长度
Npkt = 1000;
%网络译码迭代次数
Niter = 5;
per = randperm(2*Len);
SNRs = [0:2:12];
ij = 0;for i = SNRsisigma = 1/sqrt(0.5*10^(i/10));Error = 0;ij = ij+1;for k = 1:Npkt%QPSKId = round(rand(1,Len));%I路Qd = round(rand(1,Len));%Q路%网络编码Id_enc = func_enc(Id,per);Qd_enc = func_enc(Qd,per);Id_enc2= 1-2*Id_enc;Qd_enc2= 1-2*Qd_enc;Rec_ref= Id_enc2+Qd_enc2;theta1 = pi/6;Id_enc2= Id_enc2.*exp(-sqrt(-1)*theta1)+sigma*randn(1,2*Len);Qd_enc2= Qd_enc2.*exp(-sqrt(-1)*theta1)+sigma*randn(1,2*Len);%通过干扰Rec0 = Id_enc2 + Qd_enc2; %接收%MLE进行相位估计if k <= 10thest0 = atan(sum(imag(conj(Rec_ref).*Rec0))/sum(real(conj(Rec_ref).*Rec0))); thest = thest0;else%相位跟踪Rec = Rec0.*exp(sqrt(-1)*thest);err = real(mean(Rec0-Rec));C1 = 0.00015;thest = thest+C1*err;endRec = Rec0.*exp(-sqrt(-1)*thest);h = func_H(Id,per);Y = func_dec(Rec,h,1,1,sigma,Niter);Error = Error + sum(abs(mod(Id+Qd,2) - Y));endber(ij) = Error/Npkt/Len;
endfigure;
semilogy(SNRs,ber,'b-o')
xlabel('SNR(dB)');
ylabel('BER ');
grid on
save R1.mat SNRs ber
15_007m4.算法理论概述
基于物理层网络编码的相位同步算法是一种利用物理层网络编码技术来实现相位同步的算法。这种算法的原理是将两个或多个相位不同的信号进行叠加,产生一个叠加信号,然后通过分析叠加信号的相位信息来实现相位同步。
物理层网络编码
物理层网络编码是一种将两个或多个相位不同的信号进行叠加的技术。这种技术的基本原理是将两个或多个信号的振幅和相位进行适当的调整,然后将它们进行叠加,产生一个叠加信号。通过这种方式,我们可以将两个或多个信号的信息进行融合,从而提高信号的传输效率和可靠性。
相位同步算法
相位同步算法是一种用来实现两个或多个相位不同的信号同步的技术。这种技术的基本原理是通过分析信号的相位信息来实现相位同步。具体来说,我们需要对接收到的信号进行解调,然后提取出信号的相位信息。接着,我们可以通过比较不同信号的相位信息来计算它们的相位差。最后,我们可以通过调整信号的相位来消除相位差,从而实现相位同步。
基于物理层网络编码的相位同步算法的原理是将两个或多个相位不同的信号进行叠加,产生一个叠加信号。然后,我们将这个叠加信号进行解调,提取出信号的相位信息。接着,我们可以通过比较不同信号的相位信息来计算它们的相位差。最后,我们可以通过调整信号的相位来消除相位差,从而实现相位同步。
基于物理层网络编码的相位同步算法涉及到的公式比较多,下面我们只列举其中一些关键的公式:
- 信号叠加公式:s(t)=∑i=1nAi(t)cos(ωit+φi(t))
- 解调公式:y(t)=s(t)cos(θ(t))=∑i=1nAi(t)cos(ωit+φi(t))cos(θ(t))
- 相位提取公式:φ=atan2(ℑ(y),ℜ(y))
- 相位差计算公式:Δφ=atan2(ℑ(y1−y2),ℜ(y1−y2))
- 相位调整公式:φ1=φ0+Δφ
其中,s(t)表示叠加后的信号,Ai(t)和φi(t)分别表示第i个信号的振幅和相位,ωi表示第i个信号的角频率,θ(t)表示解调角度,y(t)表示解调后的信号,ℑ(y)和ℜ(y)分别表示y(t)的虚部和实部,φ表示信号的相位,Δφ表示两个信号的相位差,φ0表示参考信号的相位,φ1表示需要调整相位的信号的相位。
基于物理层网络编码的相位同步算法是一种利用物理层网络编码技术来实现相位同步的方法。这种算法通过将两个或多个相位不同的信号进行叠加,然后通过对叠加后的信号进行解调和分析来计算它们的相位差,并最终通过调整信号的相位来实现相位同步。这种算法具有较高的可靠性和传输效率,因此在通信领域具有广泛的应用前景。
5.算法完整程序工程
OOOOO
OOO
O
相关文章:

基于物理层网络编码的相位同步算法matlab仿真
目录 1.算法运行效果图预览 2.算法运行软件版本 3.部分核心程序 4.算法理论概述 5.算法完整程序工程 1.算法运行效果图预览 2.算法运行软件版本 matlab2022a 3.部分核心程序 ..........................................................................%数据长度 Len…...
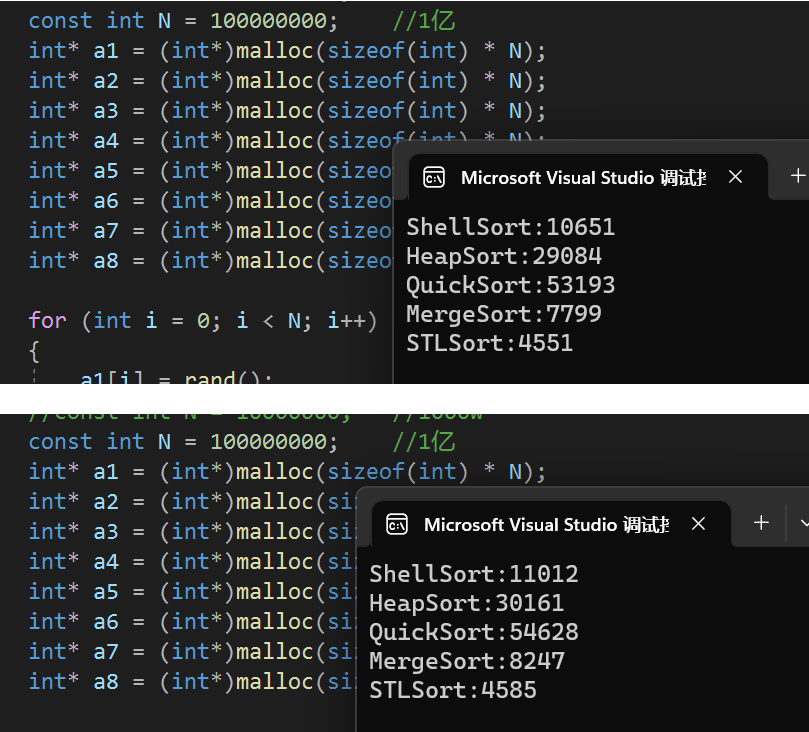
数据结构——七大排序[源码+动图+性能测试]
本章代码gitee仓库:排序 文章目录 🎃0. 思维导图🧨1. 插入排序✨1.1 直接插入排序✨1.2 希尔排序 🎊2. 选择排序🎋2.1 直接选择排序🎋2.2 堆排序 🎏3. 交换排序🎐3.1 冒泡排序&#…...
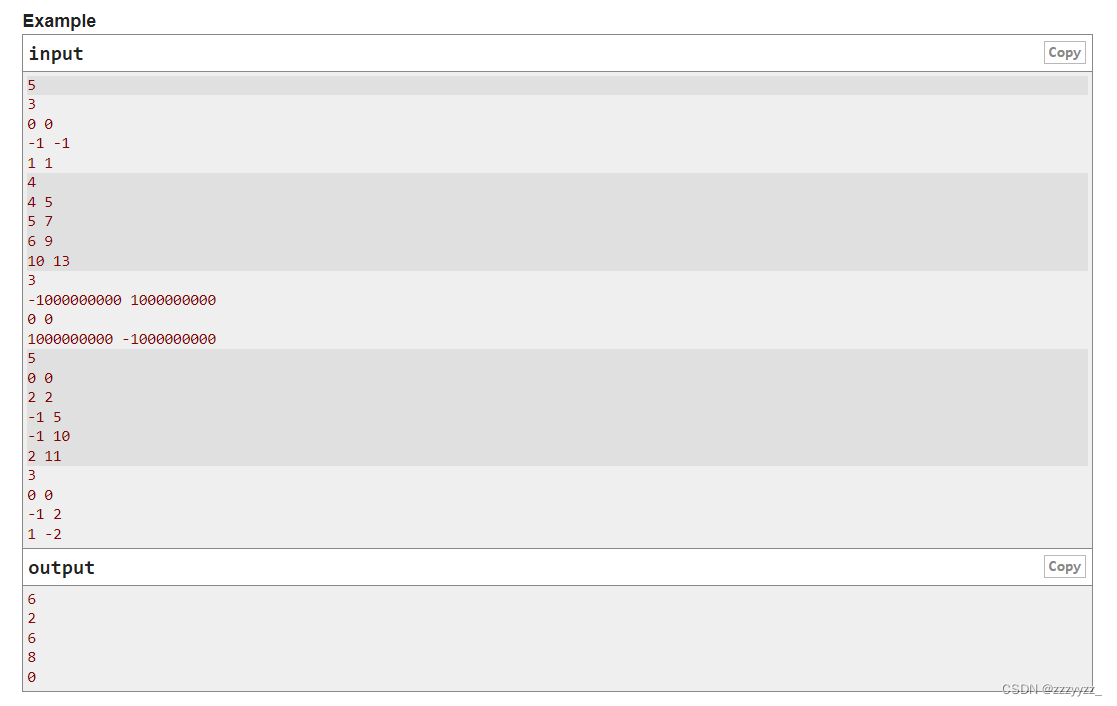
G. The Morning Star
Problem - G - Codeforces 思路:想了挺长时间的,一直没想到一个简便的方法在瞎搞。我们发现对于某个点来说,其他的点如果能够跟他匹配,那么一定在这8个方向上,而同时这8个方向其实对应这4条直线,假设点为(x…...
电池的健康状态 SOH 估计
电池的健康状态 SOH 估计 SOH(State of Health)估计通常用于描述电池的健康状态,即电池当前容量与初始容量的比值。 一种常见的SOH估计方法是基于经验的电池寿命预测方法,包括循环周期数法、安时法与加权安时法、面向事件的老化…...
详解)
Web 安全之 Permissions Policy(权限策略)详解
什么是 Permissions Policy(权限策略)? Permissions Policy 为 web 开发人员提供了明确声明哪些功能可以在网站上使用,哪些功能不能在网站上使用的机制。可以设置一组策略,用于限制站点代码可以访问的 API 或者修改浏…...

【黄啊码】nginx如何设置php运行的
禁止访问 PHP 脚本可以通过 Nginx 服务器配置中的多种方式来实现。以下是其中的一些常见方法,您可以根据实际需求选择合适的方式: 1 禁用 PHP 解析: 在 Nginx 配置中,确保 PHP 脚本无法被解析,从而禁止 PHP 执行。 lo…...

无涯教程-JavaScript - ISPMT函数
描述 ISPMT函数计算在特定投资期间支付的利息。提供此功能是为了与Lotus 1-2-3兼容。 语法 ISPMT (rate, per, nper, pv)争论 Argument描述Required/OptionalRateThe interest rate for the investment.RequiredPerThe period for which you want to find the interest, an…...

LeetCode 面试题 03.05. 栈排序
文章目录 一、题目二、C# 题解 一、题目 栈排序。 编写程序,对栈进行排序使最小元素位于栈顶。最多只能使用一个其他的临时栈存放数据,但不得将元素复制到别的数据结构(如数组)中。该栈支持如下操作:push、pop、peek 和…...
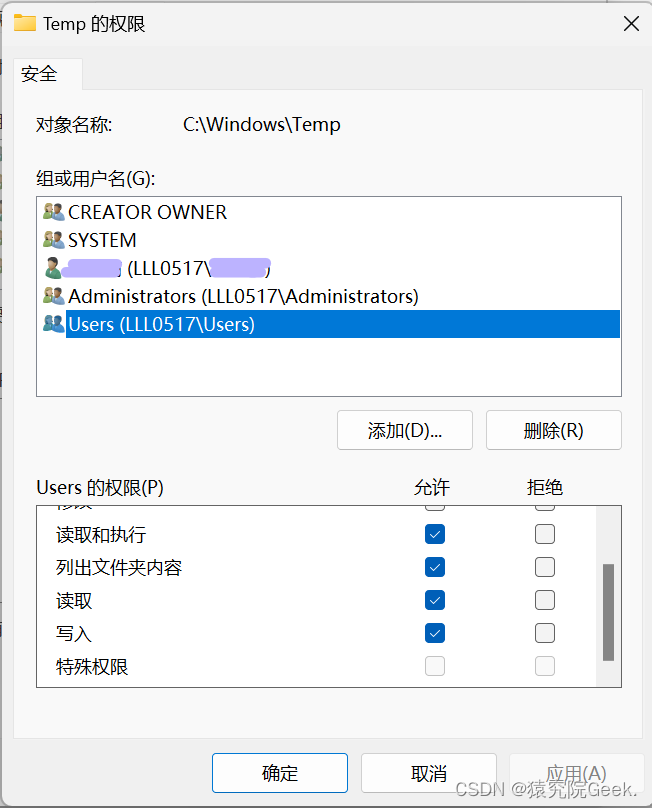
构建微服务项目时启动网关服务失败的解决方案
启动网关服务时报“Unable to create the temporary folder: C:\WINDOWS\TEMP\/nio-file-upload”错误。 代码与之前没有任何变化,但就是启动不了,观察错误意思大概是不能创建临时文件夹:C盘下的WINDOWS下的TEMP目录下的nio-file-upload这个东…...
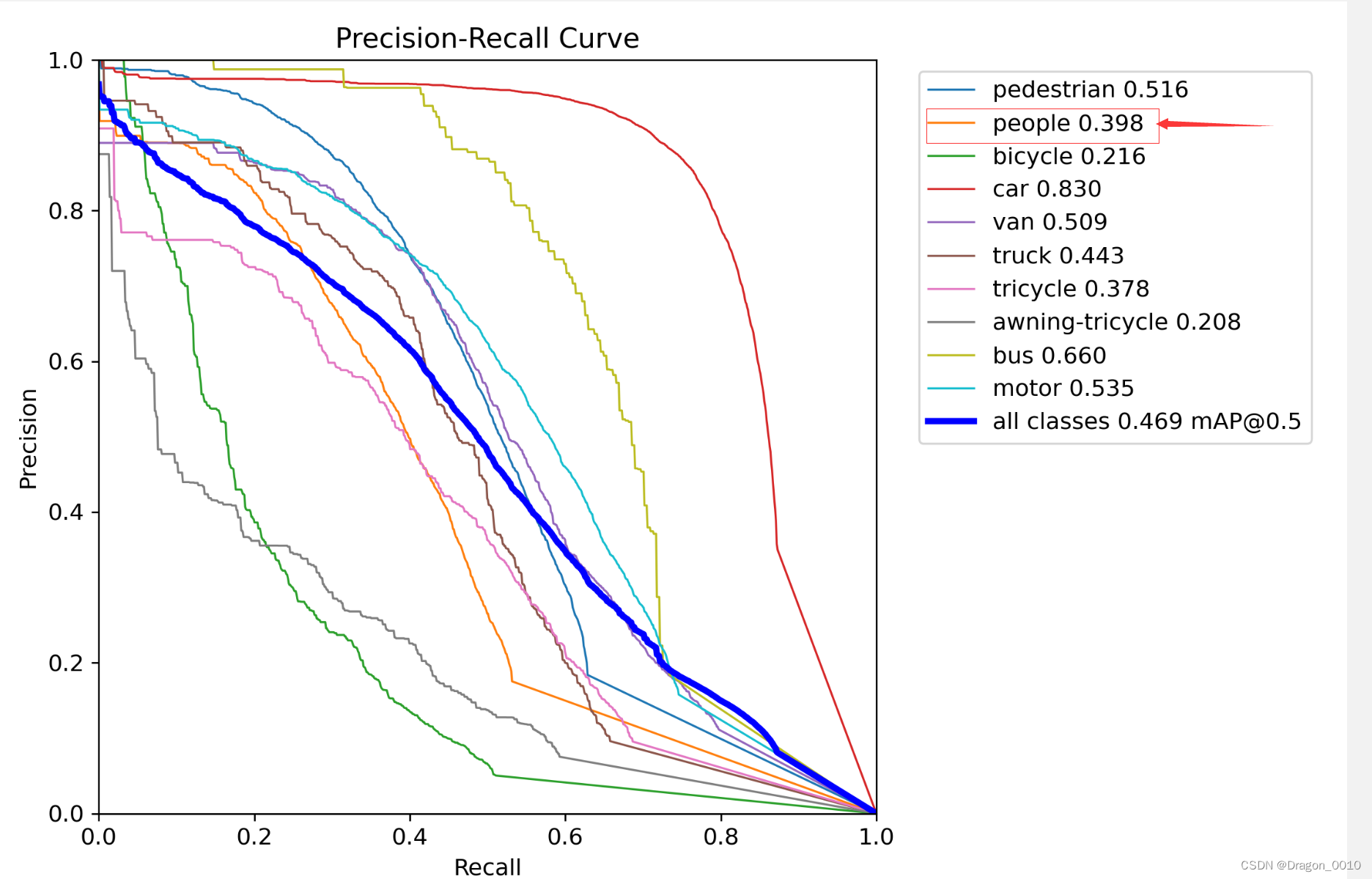
零基础教程:使用yolov8训练无人机VisDrone数据集
1.准备数据集 1.先给出VisDrone2019数据集的下载地址: 链接:https://pan.baidu.com/s/1e2Q0NgNT-H-Acb2H0Cx8sg 提取码:31dl 2.将数据集VisDrone放在datasets目录下面 2.数据集转换程序 1.在根目录下面新建一个.py文件,取名叫…...

【Mysql专题】使用Mysql做排行榜,线上实例
背景 我们这里有个需求,对存量用户的余额做排行处理,这个实现方式很多,这边介绍的是,通过Mysql直接实现,将排名也直接返回出来。 我知道大家在网上能找到一大把这种实例,我在这里可不是【重复造轮子】。我…...
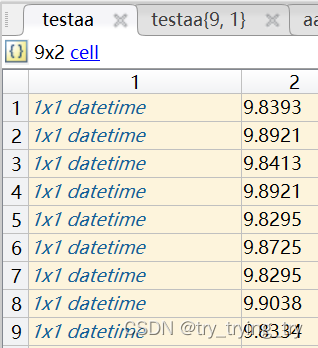
matlab数据处理: cell table array+datetime
原数据文件.csv matlab xlsread(filename{i},B2:T2881) 会同于Excel最多1048576行 舍弃 a{1,i} xlsread(filename{i},‘B2:T2881’);%读取excel文件,选定区域’B2:G2881’ readcell(filename{i},Range,E2:M2881) 会全部读取 优选 对于日期 yyyy-MM-dd HH:mm:ss.000 matlab cel…...
如何应用运营商大数据精准营销?
如何应用运营商大数据精准营销? 越来越多的企业逐渐觉察到运营商大数据所带来的商业价值,精准营销也被他们用的越来越娴熟。那么,企业的大数据精准营销该如何应用呢?想必是很多资源有限的中小型公司最想了解的。 一 数据驱动运营…...
AJAX学习笔记5同步与异步理解
AJAX学习笔记4解决乱码问题_biubiubiu0706的博客-CSDN博客 示例 前端代码 <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><title>演示AJAX同步和异步</title> </head> <body> <script…...

911面试
WebPack分包 webpack分包 ts泛型 ts泛型 优化if-else和switch 优化if-else 左侧固定,右侧自适应 左侧固定,右侧自适应...
【Java基础篇 | 面向对象】—— 继承
个人主页:兜里有颗棉花糖 欢迎 点赞👍 收藏✨ 留言✉ 加关注💓本文由 兜里有颗棉花糖 原创 收录于专栏【JavaSE_primary】 本专栏旨在分享学习JavaSE的一点学习心得,欢迎大家在评论区讨论💌 继承允许一个类继承另一个…...

DELL precision上安装nvidia A4000驱动 cuda cudnn
一、安装驱动 参考这篇文章进行安装Ubuntu安装Nvidia显卡驱动_Kevin__47的博客-CSDN博客 【出现问题】 禁用nouveau后出现黑屏,有几行代码,断线一直在闪 【解决方法】 1、参考这篇文章Ubuntu20.04安装nvidia显卡驱动并解决重启后黑屏问题_ubuntu安装…...

数据结构算法刷题(29)动态规划
思路一:回溯:按照选和不选的判断方式,使用回溯来解决这个问题。 class Solution: def rob(self, nums: List[int]) -> int: n len(nums) #数组的长度 def dfs(i): if i<0: #到达边界条件后 return 0 #返回最大金额是0 res max(dfs(i…...

W11下CMake MinGW配置OpenCV和Qt
💂 个人主页:风间琉璃🤟 版权: 本文由【风间琉璃】原创、在CSDN首发、需要转载请联系博主💬 如果文章对你有帮助、欢迎关注、点赞、收藏(一键三连)和订阅专栏哦 前言 前几天将cuda版本的opencv给编译成功了,当时用的VS的MSVC&…...

反转字符串 反转字符串 || 反转字符串 |||
思想总结:首先将字符串转变为字符数组,再进行遍历并反转字符。 1.反转字符串 代码: class Solution {public void reverseString(char[] s) {reverse(s,0,s.length); //左闭右开}public static void reverse(char[] ch,int i,int j) { 翻转函…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...
)
进程地址空间(比特课总结)
一、进程地址空间 1. 环境变量 1 )⽤户级环境变量与系统级环境变量 全局属性:环境变量具有全局属性,会被⼦进程继承。例如当bash启动⼦进程时,环 境变量会⾃动传递给⼦进程。 本地变量限制:本地变量只在当前进程(ba…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

Yolov8 目标检测蒸馏学习记录
yolov8系列模型蒸馏基本流程,代码下载:这里本人提交了一个demo:djdll/Yolov8_Distillation: Yolov8轻量化_蒸馏代码实现 在轻量化模型设计中,**知识蒸馏(Knowledge Distillation)**被广泛应用,作为提升模型…...

LINUX 69 FTP 客服管理系统 man 5 /etc/vsftpd/vsftpd.conf
FTP 客服管理系统 实现kefu123登录,不允许匿名访问,kefu只能访问/data/kefu目录,不能查看其他目录 创建账号密码 useradd kefu echo 123|passwd -stdin kefu [rootcode caozx26420]# echo 123|passwd --stdin kefu 更改用户 kefu 的密码…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

tomcat指定使用的jdk版本
说明 有时候需要对tomcat配置指定的jdk版本号,此时,我们可以通过以下方式进行配置 设置方式 找到tomcat的bin目录中的setclasspath.bat。如果是linux系统则是setclasspath.sh set JAVA_HOMEC:\Program Files\Java\jdk8 set JRE_HOMEC:\Program Files…...
0609)
书籍“之“字形打印矩阵(8)0609
题目 给定一个矩阵matrix,按照"之"字形的方式打印这个矩阵,例如: 1 2 3 4 5 6 7 8 9 10 11 12 ”之“字形打印的结果为:1,…...
