C语言数据结构初阶(1)----时空复杂度
目录
1. 数据结构,算法的概念
2. 算法的效率
2.1 算法复杂度
3. 时间复杂度
3.1 时间复杂度的概念
3.2 大O的渐进表示法
3.3 小试牛刀
4. 算法的空间复杂度
4.1 小试牛刀
1. 数据结构,算法的概念
数据结构(Data Structure)是计算机存储、组织数据的方式,指相互之间存在一种或多种特定关系的数据元素的集合。
算法(Algorithm):就是定义良好的计算过程,他取一个或一组的值为输入,并产生出一个或一组值作为输出。简单来说算法就是一系列的计算步骤,用来将输入数据转化成输出结果。
2. 算法的效率
如何衡量一个算法的好坏呢?
假设对于斐波那契数列的第 n 项的求解有如下代码:
long long Fib(int N)
{if(N < 3)return 1;return Fib(N-1) + Fib(N-2);
} 这样的递归代码看起来十分简洁,那么是不是代码越简洁算法的效率越高呢?显然这是不正确的。那该怎么衡量一个算法的好坏呢?
2.1 算法复杂度
算法在编写成可执行程序后,运行时需要耗费时间资源和空间(内存)资源 。因此衡量一个算法的好坏,一般是从时间和空间两个维度来衡量的,即时间复杂度和空间复杂度。
时间复杂度主要衡量一个算法的运行快慢,而空间复杂度主要衡量一个算法运行所需要的额外空间。在计算机发展的早期,计算机的存储容量很小。所以对空间复杂度很是在乎。但是经过计算机行业的迅速发展,计算机的存储容量已经达到了很高的程度。所以我们如今已经不需要再特别关注一个算法的空间复杂度。
3. 时间复杂度
3.1 时间复杂度的概念
时间复杂度的定义:在计算机科学中,算法的时间复杂度是一个函数,它定量描述了该算法的运行时间。一个算法执行所耗费的时间,从理论上说,是不能算出来的,只有你把你的程序放在机器上跑起来,才能知道。但是我们需要每个算法都上机测试吗?是可以都上机测试,但是这很麻烦,所以才有了时间复杂度这个分析方式。一个算法所花费的时间与其中语句的执行次数成正比例,算法中的基本操作的执行次数,为算法的时间复杂度。
即:找到某条基本语句与问题规模N之间的数学表达式,就是算出了该算法的时间复杂度。
例如:对于如下代码,请计算Func1 中 ++count 执行了多少次?
// 请计算一下Func1中++count语句总共执行了多少次?
void Func1(int N)
{int count = 0;for (int i = 0; i < N ; ++ i){for (int j = 0; j < N ; ++ j){++count;}}for (int k = 0; k < 2 * N ; ++ k){++count;}int M = 10;while (M--){++count;}printf("%d\n", count);
}通过计算得到结果:N×N + 2×N + 10。
实际中我们计算时间复杂度时,我们其实并不一定要计算精确的执行次数,而只需要大概执行次数,那么这里我们使用大O的渐进表示法。
3.2 大O的渐进表示法
大O符号(Big O notation):是用于描述函数渐进行为的数学符号。
推导大O阶方法:
1、用常数1取代运行时间中的所有加法常数。
2、在修改后的运行次数函数中,只保留最高阶项。
3、如果最高阶项存在且不是1,则去除与这个项目相乘的常数。得到的结果就是大O阶。
使用大O的渐进表示法以后,Func1的时间复杂度为:O(N*N)。
通过上面我们会发现大O的渐进表示法去掉了那些对结果影响不大的项,简洁明了的表示出了执行次数。
另外有些算法的时间复杂度存在最好、平均和最坏情况:
最坏情况:任意输入规模的最大运行次数(上界)
平均情况:任意输入规模的期望运行次数
最好情况:任意输入规模的最小运行次数(下界)
例如:在一个长度为N数组中搜索一个数据x
最好情况:1次找到
最坏情况:N次找到
平均情况:N/2次找到
在实际中一般情况关注的是算法的最坏运行情况,所以数组中搜索数据时间复杂度为O(N)。
3.3 小试牛刀
(1):计算二分查找的时间复杂度。
// 计算BinarySearch的时间复杂度?
int BinarySearch(int* a, int n, int x)
{assert(a);int begin = 0;int end = n-1;// [begin, end]:begin和end是左闭右闭区间,因此有=号 while (begin <= end){int mid = begin + ((end-begin)>>1);if (a[mid] < x)begin = mid+1;else if (a[mid] > x)end = mid-1;elsereturn mid;}return -1;
}解:二分查找每次更新mid的位置都将查找的区间折半,因为时间复杂度是计算算法的最坏情况。易得二分查找的最坏情况就是:当区间长度为1时,查找到目标元素,或者压根查找不到该元素。分析:最坏情况是将区间的长度由 N 便到1,并且每次更新区间都是原区间的一半。可以得出公式:

注意:只有当底数为 2 时才可以简化为 log(N)。
(2):计算斐波那契递归Fib的时间复杂度。
long long Fib(size_t N)
{if(N < 3)return 1;return Fib(N-1) + Fib(N-2);
}
这道题算是时间复杂度计算的算法中比较困难的,建议画图计算。

4. 算法的空间复杂度
空间复杂度也是一个数学表达式,是对一个算法在运行过程中临时占用存储空间大小的量度。
空间复杂度不是程序占用了多少bytes的空间,因为这个也没太大意义,所以空间复杂度算的是变量的个数。空间复杂度计算规则基本跟实践复杂度类似,也使用大O渐进表示法。
注意:函数运行时所需要的栈空间(存储参数、局部变量、一些寄存器信息等)在编译期间已经确定好了,因此空间复杂度主要通过函数在运行时候显式申请的额外空间来确定。
4.1 小试牛刀
(1):计算阶乘递归Fac的空间复杂度。
long long Fac(size_t N)
{if(N == 0)return 1;return Fac(N-1)*N;
}显然每次调用Fac函数只用了常数个空间,即空间复杂度为O(1),但是,因为递归会消耗栈上的空间,且易得该函数调用了 N + 1次,根据大O的渐进表示法:最终该算法的空间复杂度为O(N)。
(2):计算斐波那契递归Fib的空间复杂度。
long long Fib(size_t N)
{if(N < 3)return 1;return Fib(N-1) + Fib(N-2);
}显然Fac()函数的每次调用消耗的额外空间为常数个,即每次调用该函数的空间复杂度为O(1),上面我们又求出了该算法的时间复杂度为O(2^N),那么是不是该算法的空间复杂度就是O(2^N),显然不会这么简单!!!

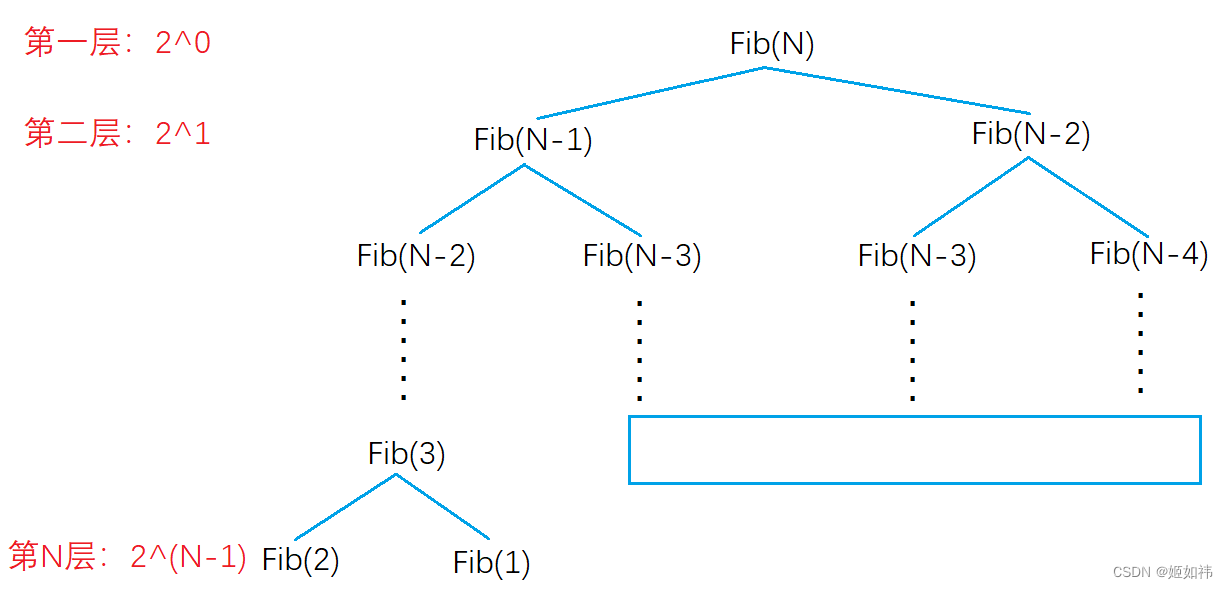
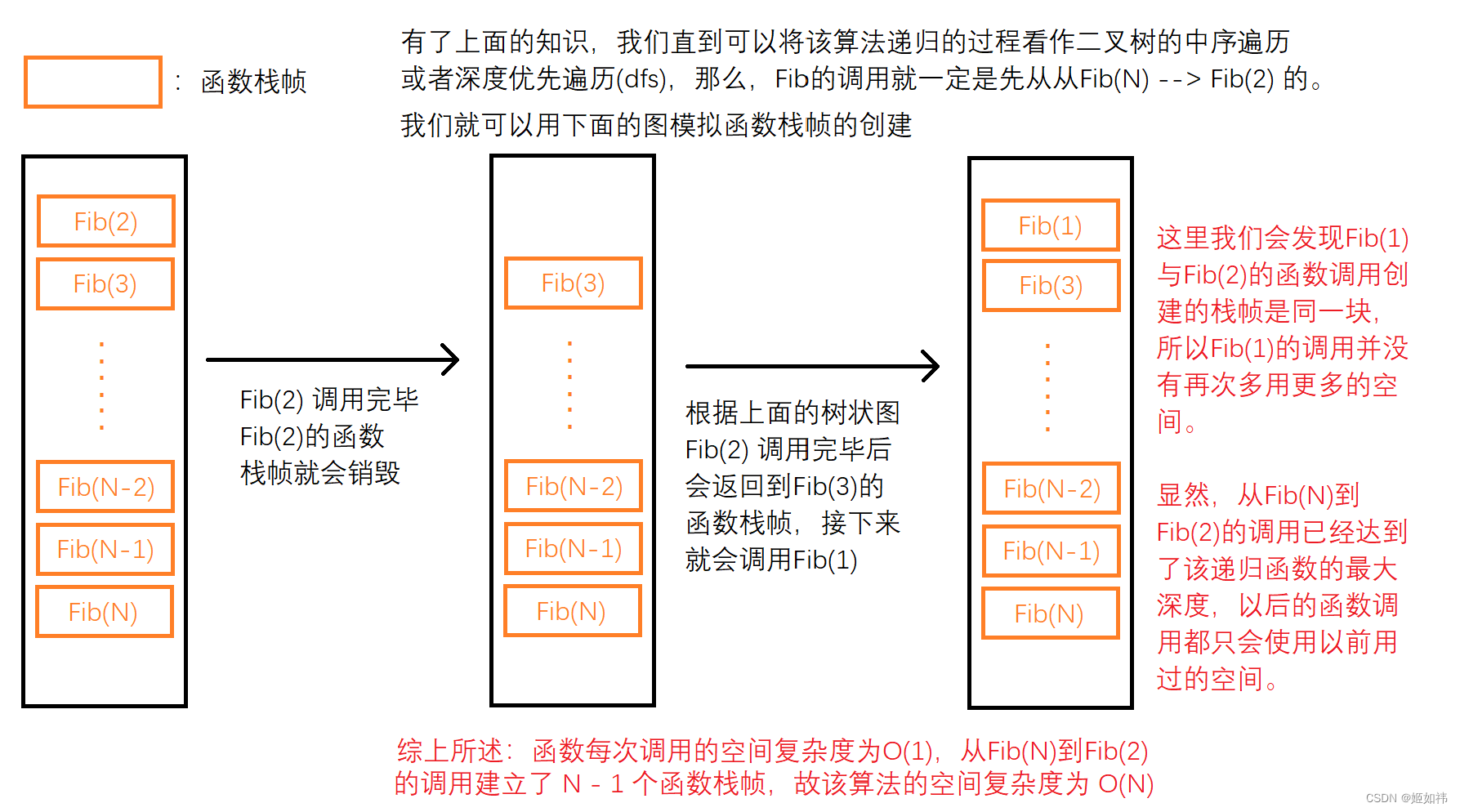
递归算法的空间复杂度取决于:每次函数调用的空间复杂度和最大递归深度
相关文章:

C语言数据结构初阶(1)----时空复杂度
目录 1. 数据结构,算法的概念 2. 算法的效率 2.1 算法复杂度 3. 时间复杂度 3.1 时间复杂度的概念 3.2 大O的渐进表示法 3.3 小试牛刀 4. 算法的空间复杂度 4.1 小试牛刀 1. 数据结构,算法的概念 数据结构(Data Structure)是计算机存储、组织数据…...
vscode SSH 保存密码自动登录服务器
先在win local上拿到秘钥,然后再把这秘钥copy 进服务器 1. 创建 RSA 密钥对 第一步是在客户端机器(通常是您的计算机 win 10)上创建密钥对:打开powershell, 输入 ssh-keygen默认情况下ssh-keygen将创建一个 2048 位 RSA 密钥对…...

VR全景多种玩法打破传统宣传,打造全新云端视界
传统的展示方式只是在进行单方面的表达,不论是图片、视频,都无法让浏览者有参与感,这样的展示宣传效果自然比不上VR全景展示,VR全景基于真实场景来形成三维图像,其沉浸式和无视野盲区的特点让用户更有真实感和沉浸感&a…...

Git 教程
目录1.简介:2.安装Git3.Git 如何工作状态区域4.使用Git5.Git配置5.1 创建仓库 - repository5.2 配置5.2.1 --global5.2.2 检查配置6. 查看工作区的文件状态6.1什么是工作区6.2 如果显示乱码的解决方式7.在工作区添加单个文件8. 添加工作区文件到暂存区9. 创建版本10…...

一种全新的图像滤波理论的实验(二)
一、前言 2021年12月31日,我发布了基于加权概率模型的图像滤波算法的第一个实验,当时有两个关键问题没有解决: 1、出现了大面积的黑色区域,最近考虑把这个算法实际应用在图像和视频的压缩领域,于是通过对程序的分析&a…...
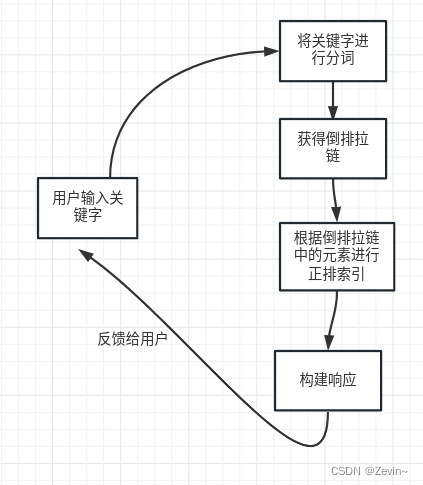
Boost库文档搜索引擎
文章目录综述效果展示去标签化,清理数据构建索引用户查询综述 该项目使用了BS架构,实现了用户对Boost库进行站内搜索的功能, 用户输入关键字使用http协议通过ajax将数据发送给后端服务器,后端进行分词, 通过倒排索引…...

Linux中安装JDK
Linux中安装JDK一 、下载JDK包1、下载网址2、往下翻,找到 java83、继续往下翻找到要下载的版本 64位linux版本二 上传jdk安装包三 开始安装整体过程1、解压文件2、查看解压文件3、进入解压文件夹确认4、配置环境变量5、重新加载环境变量6、确认安装成功一 、下载JDK…...
宝塔面板公网ip非80端口非443端口部署ssl
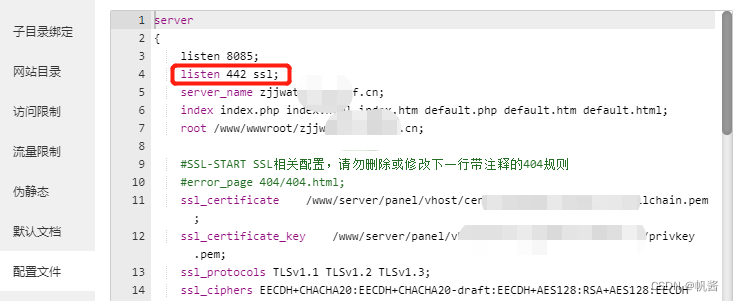
有不少人使用家用宽带,虽然申请下来了公网ip,但是运营商封了80与443端口,但仍想使用ssl证书 一、仅封80端口 1、先在宝塔面板里创建网站,域名为test.xxx.cn:8085 2、再到域名运营商做A记录解析,此时可以通过http://…...

手撕八大排序(上)
排序的概念及其引用: 排序的概念: 排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。 稳定性:假定在待排序的记录序列中,存在多个具有…...

clickhouse 怎么统计每天0点到10点的某个字段的数据量
比喻:统计最近一周0点到10点期间每天id的数量 日期:2023-03-23 09:02:22 日期全是这种格式 第一步先把日期转小时:先把小于10小时的查出来 toHour(card_time)<10 select toDate(t.dates) as dates,sum(t.count) as count from ( se…...

[qiankun]-图片加载问题
[qiankun]-图片加载问题开发版本图片加载报错现象描述分析解决方案base64的展示格式静态资源的展示方式取消hash的取值方式,并在主应用中添加图片设置图片的绝对路径根据环境动态设置图片的绝对路径nginx转发方式开发版本 "vue": "^3.2.45", &…...
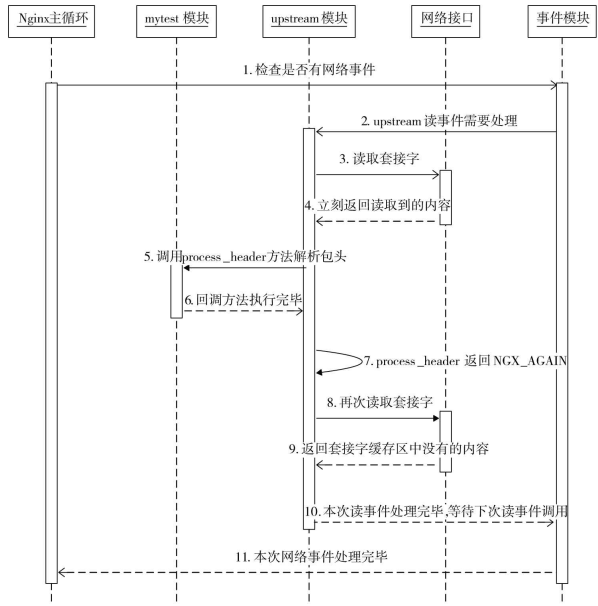
关于upstream的八种回调方法
1 creat_request调用背景:用于创建自己模板与第三方服务器的第一次连接步骤1) 在Nginx主循环(ngx_worker_process_cycle方法) 中,会定期地调用事件模块, 以检查是否有网络事件发生。2) 事件模块…...

0303泰勒公式-微分中值定理与导数的应用
文章目录1 引入2 泰勒中值定理2.1 泰勒多项式3.2 泰勒中值定理13.3 泰勒中值定理22.4 误差估计4 麦克劳林公式5 常见麦克劳林公式6 泰勒公式相关例题6.1 将函数展成指定的泰勒公式6.1.1 公式法6.1.2 间接展法(变量替换)6.2 利用泰勒公式求极限6.3 确定无…...

日常运维基础命令
commandexplainps -f -u user_name显示指定用户的进程ps aux --sort-pcpu,pmem先以cpu使用量进行排序,cpu使 用一样,以内存使用率排序ps -ef --forest显示ACLII进程数ps --ppid 28208显示父进程的子进程ps -p 14447 -L显示进程的线程ps -e -o pid&#x…...
人员行为识别系统 TensorFlow
人员行为识别系统人员行为识别系统通过TensorFlow深度学习技术,人员行为识别算法对画面中区域人员不按要求穿戴、违规抽烟打电话、睡岗离岗以及作业流程不规范实时分析预警,发现违规行为立即抓拍告警。深度学习应用到实际问题中,一个非常棘手…...

ES-倒排索引BKD原理skiplist
1.Elasticsearch数据存储结构FST、skiplist、BKD-tree、LSM-tree Elasticsearch数据结构存储流程_善思的博客-CSDN博客_elasticsearch 数据结构 number?keyword?傻傻分不清楚 - Elastic 中文社区 ElasticSearch实战(六)-Skip List 跳表算法…...
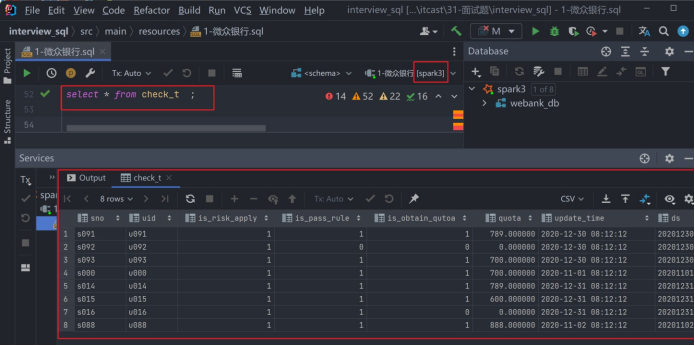
每天一道大厂SQL题【Day12】微众银行真题实战(二)
每天一道大厂SQL题【Day12】微众银行真题实战(二) 大家好,我是Maynor。相信大家和我一样,都有一个大厂梦,作为一名资深大数据选手,深知SQL重要性,接下来我准备用100天时间,基于大数据岗面试中的经典SQL题&…...
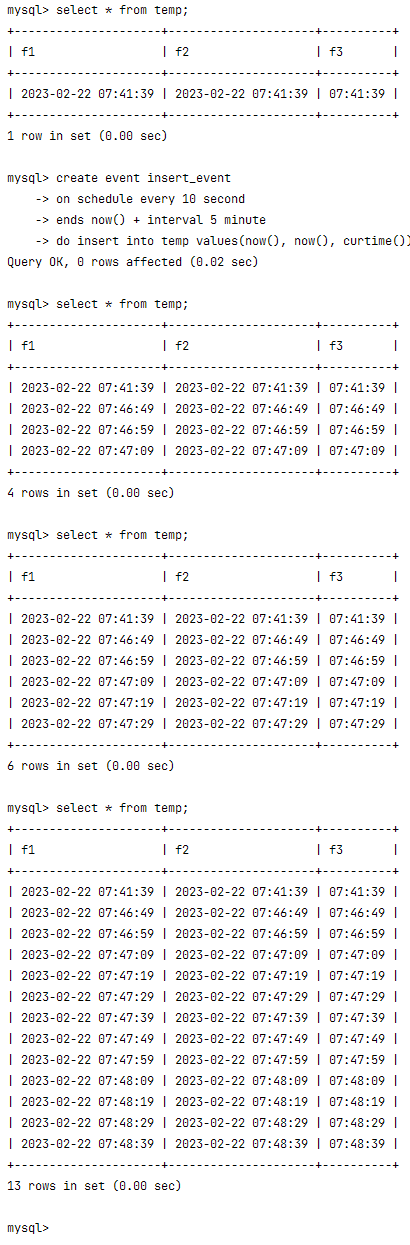
带您了解TiDB MySQL数据库中关于日期、时间的坑
带您了解TiDB & MySQL数据库中关于日期、时间的坑时间的基础知识什么是时间计算时间的几种方法世界时(UT)协调世界时(UTC)国际原子时(TAI)时区的概念中国所在的时区操作系统的时区datetimedatectl数据库…...

【华为OD机试模拟题】用 C++ 实现 - 求字符串中所有整数的最小和
最近更新的博客 华为OD机试 - 入栈出栈(C++) | 附带编码思路 【2023】 华为OD机试 - 箱子之形摆放(C++) | 附带编码思路 【2023】 华为OD机试 - 简易内存池 2(C++) | 附带编码思路 【2023】 华为OD机试 - 第 N 个排列(C++) | 附带编码思路 【2023】 华为OD机试 - 考古…...
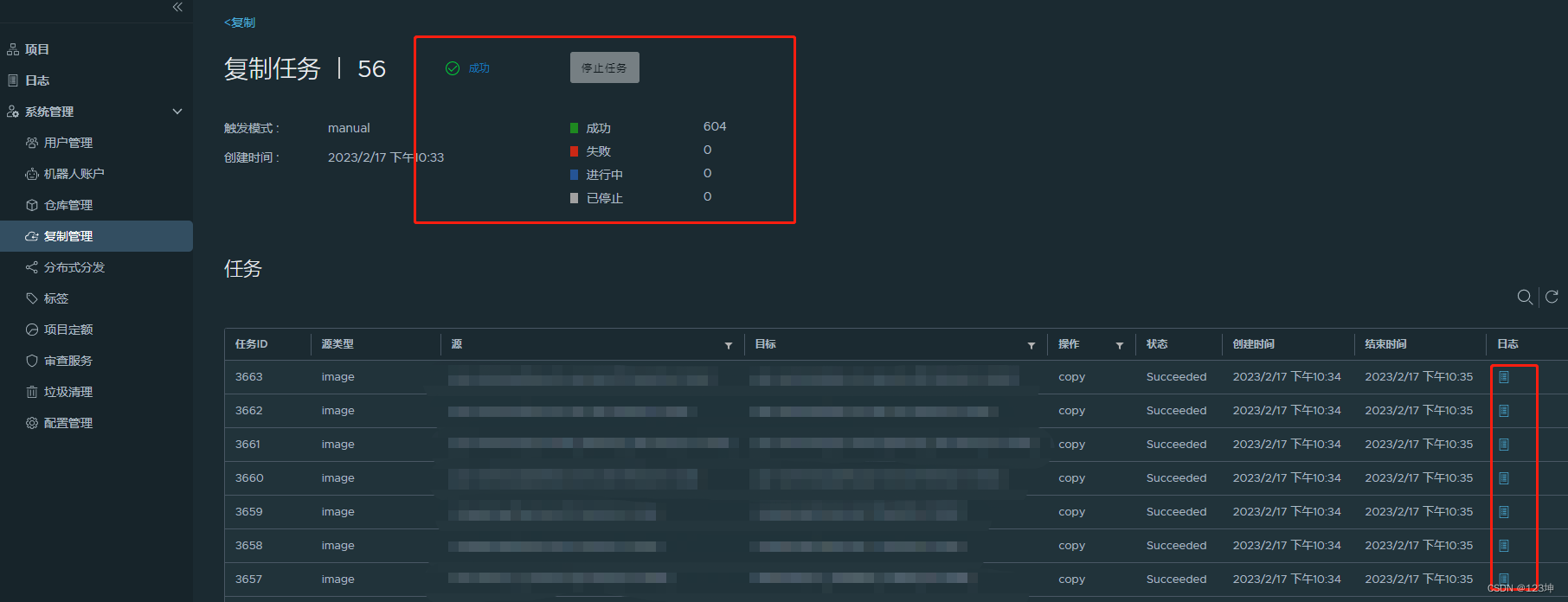
harbor 仓库迁移升级
harbor 仓库迁移升级 harbor仓库安装数据传输仓库切换版本 v1.8.0 v2.3.5 harbor仓库安装 环境准备:安装docker详见:docker 的介绍和部署,并下载docker-compose详见:docker 三剑客compose。 现有支持的安装harbor仓库的方式有两…...
)
云计算——弹性云计算器(ECS)
弹性云服务器:ECS 概述 云计算重构了ICT系统,云计算平台厂商推出使得厂家能够主要关注应用管理而非平台管理的云平台,包含如下主要概念。 ECS(Elastic Cloud Server):即弹性云服务器,是云计算…...

MySQL 隔离级别:脏读、幻读及不可重复读的原理与示例
一、MySQL 隔离级别 MySQL 提供了四种隔离级别,用于控制事务之间的并发访问以及数据的可见性,不同隔离级别对脏读、幻读、不可重复读这几种并发数据问题有着不同的处理方式,具体如下: 隔离级别脏读不可重复读幻读性能特点及锁机制读未提交(READ UNCOMMITTED)允许出现允许…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

【决胜公务员考试】求职OMG——见面课测验1
2025最新版!!!6.8截至答题,大家注意呀! 博主码字不易点个关注吧,祝期末顺利~~ 1.单选题(2分) 下列说法错误的是:( B ) A.选调生属于公务员系统 B.公务员属于事业编 C.选调生有基层锻炼的要求 D…...

AI书签管理工具开发全记录(十九):嵌入资源处理
1.前言 📝 在上一篇文章中,我们完成了书签的导入导出功能。本篇文章我们研究如何处理嵌入资源,方便后续将资源打包到一个可执行文件中。 2.embed介绍 🎯 Go 1.16 引入了革命性的 embed 包,彻底改变了静态资源管理的…...

脑机新手指南(七):OpenBCI_GUI:从环境搭建到数据可视化(上)
一、OpenBCI_GUI 项目概述 (一)项目背景与目标 OpenBCI 是一个开源的脑电信号采集硬件平台,其配套的 OpenBCI_GUI 则是专为该硬件设计的图形化界面工具。对于研究人员、开发者和学生而言,首次接触 OpenBCI 设备时,往…...
与文本切分器(Splitter)详解《二》)
LangChain 中的文档加载器(Loader)与文本切分器(Splitter)详解《二》
🧠 LangChain 中 TextSplitter 的使用详解:从基础到进阶(附代码) 一、前言 在处理大规模文本数据时,特别是在构建知识库或进行大模型训练与推理时,文本切分(Text Splitting) 是一个…...

JS红宝书笔记 - 3.3 变量
要定义变量,可以使用var操作符,后跟变量名 ES实现变量初始化,因此可以同时定义变量并设置它的值 使用var操作符定义的变量会成为包含它的函数的局部变量。 在函数内定义变量时省略var操作符,可以创建一个全局变量 如果需要定义…...

深入解析光敏传感技术:嵌入式仿真平台如何重塑电子工程教学
一、光敏传感技术的物理本质与系统级实现挑战 光敏电阻作为经典的光电传感器件,其工作原理根植于半导体材料的光电导效应。当入射光子能量超过材料带隙宽度时,价带电子受激发跃迁至导带,形成电子-空穴对,导致材料电导率显著提升。…...
