day38 动态规划 | 509、斐波那契数 70、爬楼梯 746、使用最小花费爬楼梯
题目
509、斐波那契数
斐波那契数,通常用 F(n) 表示,形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是: F(0) = 0,F(1) = 1 F(n) = F(n - 1) + F(n - 2),其中 n > 1 给你n ,请计算 F(n) 。
示例 1:
输入:2
输出:1
解释:F(2) = F(1) + F(0) = 1 + 0 = 1
示例 2:
输入:3
输出:2
解释:F(3) = F(2) + F(1) = 1 + 1 = 2
示例 3:
输入:4
输出:3
解释:F(4) = F(3) + F(2) = 2 + 1 = 3
提示:
0 <= n <= 30
class Solution {public int fib(int n) {if (n < 2) return n;int a = 0, b = 1, c = 0;for (int i = 1; i < n; i++) {c = a + b;a = b;b = c;}return c;}
}
//非压缩状态的版本
class Solution {public int fib(int n) {if (n <= 1) return n; int[] dp = new int[n + 1];dp[0] = 0;dp[1] = 1;for (int index = 2; index <= n; index++){dp[index] = dp[index - 1] + dp[index - 2];}return dp[n];}
}
70、爬楼梯
假设你正在爬楼梯。需要 n 阶你才能到达楼顶。
每次你可以爬 1 或 2 个台阶。你有多少种不同的方法可以爬到楼顶呢?
注意:给定 n 是一个正整数。
示例 1:
输入: 2
输出: 2
解释: 有两种方法可以爬到楼顶。
1 阶 + 1 阶
2 阶
示例 2:
输入: 3
输出: 3
解释: 有三种方法可以爬到楼顶。
1 阶 + 1 阶 + 1 阶
1 阶 + 2 阶
2 阶 + 1 阶
// 常规方式
public int climbStairs(int n) {int[] dp = new int[n + 1];dp[0] = 1;dp[1] = 1;for (int i = 2; i <= n; i++) {dp[i] = dp[i - 1] + dp[i - 2];}return dp[n];
}
// 用变量记录代替数组
class Solution {public int climbStairs(int n) {if(n <= 2) return n;int a = 1, b = 2, sum = 0;for(int i = 3; i <= n; i++){sum = a + b; // f(i - 1) + f(i - 2)a = b; // 记录f(i - 1),即下一轮的f(i - 2)b = sum; // 记录f(i),即下一轮的f(i - 1)}return b;}
}
746、使用最小花费爬楼梯
数组的每个下标作为一个阶梯,第 i 个阶梯对应着一个非负数的体力花费值 cost[i](下标从 0 开始)。
每当你爬上一个阶梯你都要花费对应的体力值,一旦支付了相应的体力值,你就可以选择向上爬一个阶梯或者爬两个阶梯。
请你找出达到楼层顶部的最低花费。在开始时,你可以选择从下标为 0 或 1 的元素作为初始阶梯。
示例 1:
输入:cost = [10, 15, 20]
输出:15
解释:最低花费是从 cost[1] 开始,然后走两步即可到阶梯顶,一共花费 15 。
示例 2:
输入:cost = [1, 100, 1, 1, 1, 100, 1, 1, 100, 1]
输出:6
解释:最低花费方式是从 cost[0] 开始,逐个经过那些 1 ,跳过 cost[3] ,一共花费 6 。
提示:
cost 的长度范围是 [2, 1000]。
cost[i] 将会是一个整型数据,范围为 [0, 999] 。
// 方式一:第一步不支付费用
class Solution {public int minCostClimbingStairs(int[] cost) {int len = cost.length;int[] dp = new int[len + 1];// 从下标为 0 或下标为 1 的台阶开始,因此支付费用为0dp[0] = 0;dp[1] = 0;// 计算到达每一层台阶的最小费用for (int i = 2; i <= len; i++) {dp[i] = Math.min(dp[i - 1] + cost[i - 1], dp[i - 2] + cost[i - 2]);}return dp[len];}
}
// 方式二:第一步支付费用
class Solution {public int minCostClimbingStairs(int[] cost) {int[] dp = new int[cost.length];dp[0] = cost[0];dp[1] = cost[1];for (int i = 2; i < cost.length; i++) {dp[i] = Math.min(dp[i - 1], dp[i - 2]) + cost[i];}//最后一步,如果是由倒数第二步爬,则最后一步的体力花费可以不用算return Math.min(dp[cost.length - 1], dp[cost.length - 2]);}
}
相关文章:

day38 动态规划 | 509、斐波那契数 70、爬楼梯 746、使用最小花费爬楼梯
题目 509、斐波那契数 斐波那契数,通常用 F(n) 表示,形成的序列称为 斐波那契数列 。该数列由 0 和 1 开始,后面的每一项数字都是前面两项数字的和。也就是: F(0) 0,F(1) 1 F(n) F(n - 1) F(n - 2),其…...

2023年备考软考必须知道的6件事
不知不觉,距离2023年上半年软考也只有不到100天的时间了,报名入口也将在3月13日正式开通,你是正在犹豫是否参加考试? 还是已经开始着手准备复习? 关于软考考试你还有哪些疑问? 2023年备考软考必须知道的6件事,建议收藏…...

GLOG如何控制输出的小数点位数
1 问题 在小白的蹩脚翻译演绎型博文《GLOG从入门到入门》中,有位热心读者提问说:在保存日志时,浮点型变量的小数位数如何设置? 首先感谢这位“嘻嘻哈哈的地球人”赏光阅读了小白这不太通顺的博客文章,并提出了一个很…...
2022年全国职业院校技能大赛(中职组)网络安全竞赛试题A(6)
目录 模块A 基础设施设置与安全加固 一、项目和任务描述: 二、服务器环境说明 三、具体任务(每个任务得分以电子答题卡为准) A-1任务一:登录安全加固(Windows) 1.密码策略 a.密码策略必须同时满足大小…...

Safety-Gym环境配置与安
官网: https://github.com/openai/safety-gym https://github.com/openai/safety-starter-agents 一、安装依赖环境配置 建议使用python 3.7及以下环境,因为官方的safety-rl是基于tensorflow1.13.1实现,而tensorflow1.13.1只能支持python…...
3月再不跳槽,就晚了
从时间节点上来看,3月、4月是每年跳槽的黄金季! 以 BAT 为代表的互联网大厂,无论是薪资待遇、还是平台和福利,都一直是求职者眼中的香饽饽,“大厂经历” 在国内就业环境中无异于一块金子招牌。在这金三银四的时间里&a…...
HTTP cookie格式与约束
cookie是前端编程当中经常要使用到的概念,我们可以使用cookie利用浏览器来存放用户的状态信息保存用户做了一些什么事情。session是服务器端维护的状态。session又是如何和cookie关联起来。后面介绍cookie和session的使用。Cookie 是什么?RFC6265, HTTP …...

docker基础
docker基础 docker概述 docker的出现?docker解决思想docker历史docker链接docker能干什么?开发-运维 docker安装 镜像(image)容器(container)仓库(repository)底层原理 docker命令 帮助命令镜像命令 docker-images查看所有本地主机上的镜像docker-searc…...

【微信小程序】--JSON 配置文件作用(三)
💌 所属专栏:【微信小程序开发教程】 😀 作 者:我是夜阑的狗🐶 🚀 个人简介:一个正在努力学技术的CV工程师,专注基础和实战分享 ,欢迎咨询! &#…...

EDA-课设
EDA-课程设计-电子闹钟 一、实验目的 1.掌握多层电路在 QuartusII 集成开发环境中的实现; 2.熟练掌握基于 QuartusII 集成开发环境的组合逻辑电路设计流程; 3.掌握基于 QuartusII 集成开发环境的时序逻辑电路设计流程; 4.理解有限状态机设计…...

C/C++每日一练(20230222)
目录 1. 部分复制字符串(★) 2. 按字典顺序排列问题(★★) 3. 地下城游戏(★★★) 附录 动态规划 1. 部分复制字符串 将字符串2小写字母复制到字符串1:编写程序,输入字符串s2,将其中所有小写字母复制到字符串数组strl中。例如:aal1bb22cc33de4AA55…...
Java API 文档搜索引擎
1. 认识搜索引擎:在搜狗搜索的搜索结果页中, 包含了若干条结果, 每一个结果包含了图标, 标题, 描述, 展示URL等搜索引擎的本质:输入一个查询词, 得到若干个搜索结果, 每个搜索结果包含了标题, 描述, 展示URL和点击URL2. 搜索引擎思路:2.1 搜索的核心思路:当前我们有很多的网页(…...
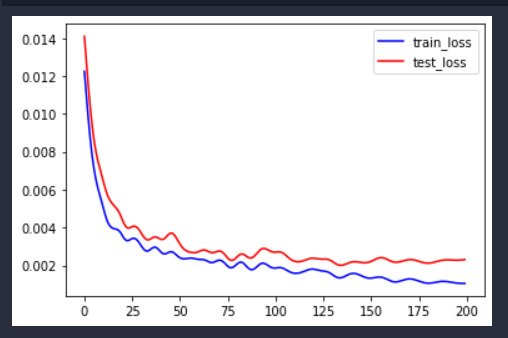
2023美赛C题Wordle二三问分布预测和难度分类预测
文章目录前言题目介绍人数分布预测首先建立字母词典,加上时间特征数据预处理训练和预测函数保存模型函数位置编码模型及其参数设置模型训练以及训练曲线可视化预测人数分布难度分类预测总结前言 2023美赛选了C题,应该很多人会选,一看就好做&…...
gdb的简单练习
题目来自《ctf安全竞赛入门》1.用vim写代码vim gdb.c#include "stdio.h" #include "stdlib.h" void main() {int i 100;int j 101;if (i j){printf("bingooooooooo.");system("/bin/sh");}elseprintf("error............&quo…...

如何使用python AI快速比对两张人脸图像?
本篇文章的代码块的实现主要是为了能够快速的通过python第三方非标准库对比出两张人脸是否一样。 实现过程比较简单,但是第三方python依赖的安装过程较为曲折,下面是通过实践对比总结出来的能够支持的几个版本,避免大家踩坑。 python版本&a…...
C#传智:变量基础(第二天))
(2)C#传智:变量基础(第二天)
一、注释符 不写注释是流氓,名字瞎起是扯蛋。 注释作用:解释与注销 命名: 以字母、_、开头,里面只能有_与特殊符,其它不得出现如%*&^等。 不能与关键字重复。区分大小写,Num…...
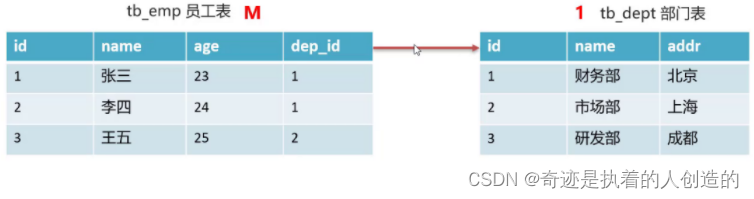
02-mysql高级-
文章目录mysql高级1,约束1.1 概念1.2 分类1.3 非空约束1.4 唯一约束1.5 主键约束1.6 默认约束1.7 约束练习1.8 外键约束1.8.1 概述1.8.2 语法1.8.3 练习2,数据库设计2.1 数据库设计简介2.2 表关系(一对多)mysql高级 今日目标 掌握约束的使用 掌握表关系…...
存储空间占用)
windows 使用everything 查看文件(夹)存储空间占用
起因 总是那个原因,C: D: E:全都红了,下的游戏太多了,然后就这样了,之前也有过不少这种情况.几年前,就在智能手机上见过类似的功能. 大概就是遍历文件系统,统计每个文件的大小,然后父节点记录所有子节点的和,然后可以显示占用百分比之类的. 经过 在windows 上我最开始使用ex…...

2023该好好赚钱了,推荐三个下班就能做的副业
在过去的两年里,越来越多的同事选择辞职创业。许多人通过互联网红利赚到了他们的第一桶金。随着短视频的兴起,越来越多的人吹嘘自己年收入百万,导致很多刚进入职场的年轻人逐渐迷失自我,认为钱特别容易赚。但事实上,80…...

vue3如何进行数据监听watch/watchEffect
我们都知道监听器的作用是在每次响应式状态发生变化时触发,在组合式 API 中,我们可以使用 watch()函数和watchEffect()函数, 当你更改了响应式状态,它可能会同时触发 Vue 组件更新和侦听器回调。 默认情况下,用户创建的侦听器回…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

unix/linux,sudo,其发展历程详细时间线、由来、历史背景
sudo 的诞生和演化,本身就是一部 Unix/Linux 系统管理哲学变迁的微缩史。来,让我们拨开时间的迷雾,一同探寻 sudo 那波澜壮阔(也颇为实用主义)的发展历程。 历史背景:su的时代与困境 ( 20 世纪 70 年代 - 80 年代初) 在 sudo 出现之前,Unix 系统管理员和需要特权操作的…...

【C++特殊工具与技术】优化内存分配(一):C++中的内存分配
目录 一、C 内存的基本概念 1.1 内存的物理与逻辑结构 1.2 C 程序的内存区域划分 二、栈内存分配 2.1 栈内存的特点 2.2 栈内存分配示例 三、堆内存分配 3.1 new和delete操作符 4.2 内存泄漏与悬空指针问题 4.3 new和delete的重载 四、智能指针…...

算法250609 高精度
加法 #include<stdio.h> #include<iostream> #include<string.h> #include<math.h> #include<algorithm> using namespace std; char input1[205]; char input2[205]; int main(){while(scanf("%s%s",input1,input2)!EOF){int a[205]…...
——统计抽样学习笔记(考试用))
统计学(第8版)——统计抽样学习笔记(考试用)
一、统计抽样的核心内容与问题 研究内容 从总体中科学抽取样本的方法利用样本数据推断总体特征(均值、比率、总量)控制抽样误差与非抽样误差 解决的核心问题 在成本约束下,用少量样本准确推断总体特征量化估计结果的可靠性(置…...

无需布线的革命:电力载波技术赋能楼宇自控系统-亚川科技
无需布线的革命:电力载波技术赋能楼宇自控系统 在楼宇自动化领域,传统控制系统依赖复杂的专用通信线路,不仅施工成本高昂,后期维护和扩展也极为不便。电力载波技术(PLC)的突破性应用,彻底改变了…...

基于谷歌ADK的 智能产品推荐系统(2): 模块功能详解
在我的上一篇博客:基于谷歌ADK的 智能产品推荐系统(1): 功能简介-CSDN博客 中我们介绍了个性化购物 Agent 项目,该项目展示了一个强大的框架,旨在模拟和实现在线购物环境中的智能导购。它不仅仅是一个简单的聊天机器人,更是一个集…...

【Zephyr 系列 16】构建 BLE + LoRa 协同通信系统:网关转发与混合调度实战
🧠关键词:Zephyr、BLE、LoRa、混合通信、事件驱动、网关中继、低功耗调度 📌面向读者:希望将 BLE 和 LoRa 结合应用于资产追踪、环境监测、远程数据采集等场景的开发者 📊篇幅预计:5300+ 字 🧭 背景与需求 在许多 IoT 项目中,单一通信方式往往难以兼顾近场数据采集…...
