R语言贝叶斯METROPOLIS-HASTINGS GIBBS 吉布斯采样器估计变点指数分布分析泊松过程车站等待时间...
原文链接:http://tecdat.cn/?p=26578
指数分布是泊松过程中事件之间时间的概率分布,因此它用于预测到下一个事件的等待时间,例如,您需要在公共汽车站等待的时间,直到下一班车到了(点击文末“阅读原文”获取完整代码数据)。
相关视频
在本文中,我们将使用指数分布,假设它的参数 λ ,即事件之间的平均时间,在某个时间点 k 发生了变化,即:
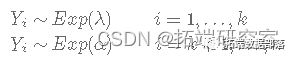
我们的主要目标是使用 Gibbs 采样器在给定来自该分布的 n 个观测样本的情况下估计参数 λ、α 和 k。
吉布斯Gibbs 采样器
Gibbs 采样器是 Metropolis-Hastings 采样器的一个特例,通常在目标是多元分布时使用。使用这种方法,链是通过从目标分布的边缘分布中采样生成的,因此每个候选点都被接受。
Gibbs 采样器生成马尔可夫链如下:
让
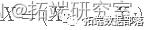 是 Rd 中的随机向量,在时间 t=0 初始化 X(0)。
是 Rd 中的随机向量,在时间 t=0 初始化 X(0)。对于每次迭代 t=1,2,3,...重复:
设置 x1=X1(t-1)。
对于每个 j=1,...,d:
生成 X∗j(t) 从
 , 其中
, 其中  是给定 X(-j) 的 Xj的单变量条件密度。
是给定 X(-j) 的 Xj的单变量条件密度。更新
 .
.当每个候选点都被接受时,设置
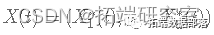 .
.增加 t。
贝叶斯公式
变点问题的一个简单公式假设 f和 g 已知密度:
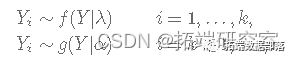
其中 k 未知且 k=1,2,...,n。让 Yi为公交车到达公交车站之间经过的时间(以分钟为单位)。假设变化点发生在第 k分钟,即:

当 Y=(Y1,Y2,...,Yn) 时,似然 L(Y|k)由下式给出:
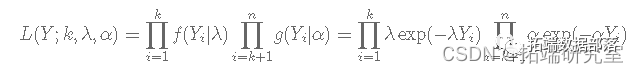
假设具有独立先验的贝叶斯模型由下式给出:

数据和参数的联合分布为:
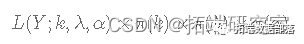
其中,
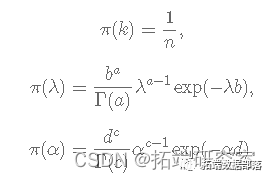
正如我之前提到的,Gibbs 采样器的实现需要从目标分布的边缘分布中采样,因此我们需要找到 λ、α 和 k 的完整条件分布。你怎么能这样做?简单来说,您必须从上面介绍的连接分布中选择仅依赖于感兴趣参数的项并忽略其余项。
相关视频
λ 的完整条件分布由下式给出:
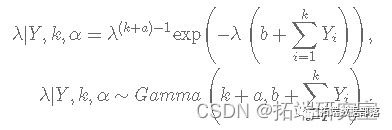
α 的完整条件分布由下式给出:
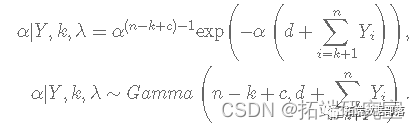
k 的完整条件分布由下式给出:
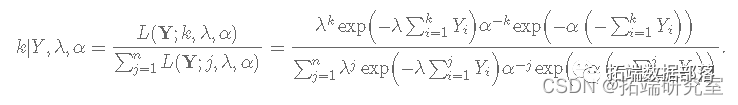
计算方法
在这里,您将学习如何使用使用 R 的 Gibbs 采样器来估计参数 λ、α 和 k。
数据
首先,我们从具有变化点的下一个指数分布生成数据:
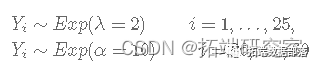
set.seed(98712)
y <- c(rexp(25, rate = 2), rexp(35, rate = 10))考虑到公交车站的情况,一开始公交车平均每2分钟一班,但从时间i=26开始,公交车开始平均每10分钟一班到公交车站。
点击标题查阅往期内容


左右滑动查看更多

01
02
03

04

Gibbs采样器的实现
首先,我们需要初始化 k、λ 和 α。
n <- length(y) # 样本的观察值的数量
lci <- 10000 # 链的大小
aba <- alpha <- k <- numeric(lcan)
k\[1\] <- sample(1:n,现在,对于算法的每次迭代,我们需要生成 λ(t)、α(t) 和 k(t),如下所示(记住如果 k+1>n 没有变化点):
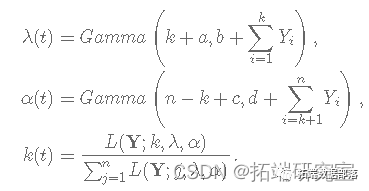
for (i in 2:lcan){kt <- k\[i-1\]# 生成lambdalambda\[i\] <- rgamma# 生成α# 产生k for (j in 1:n) {L\[j\] <- ((lambda\[i\] / alpha\[i# 删除链条上的前9000个值
bunIn <- 9000结果
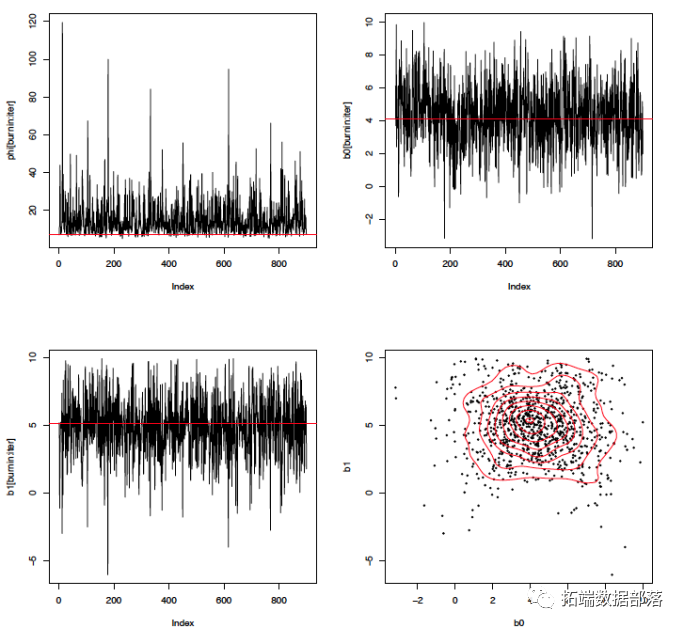
在本节中,我们将介绍 Gibbs 采样器生成的链及其参数 λ、α 和 k 的分布。参数的真实值用红线表示。
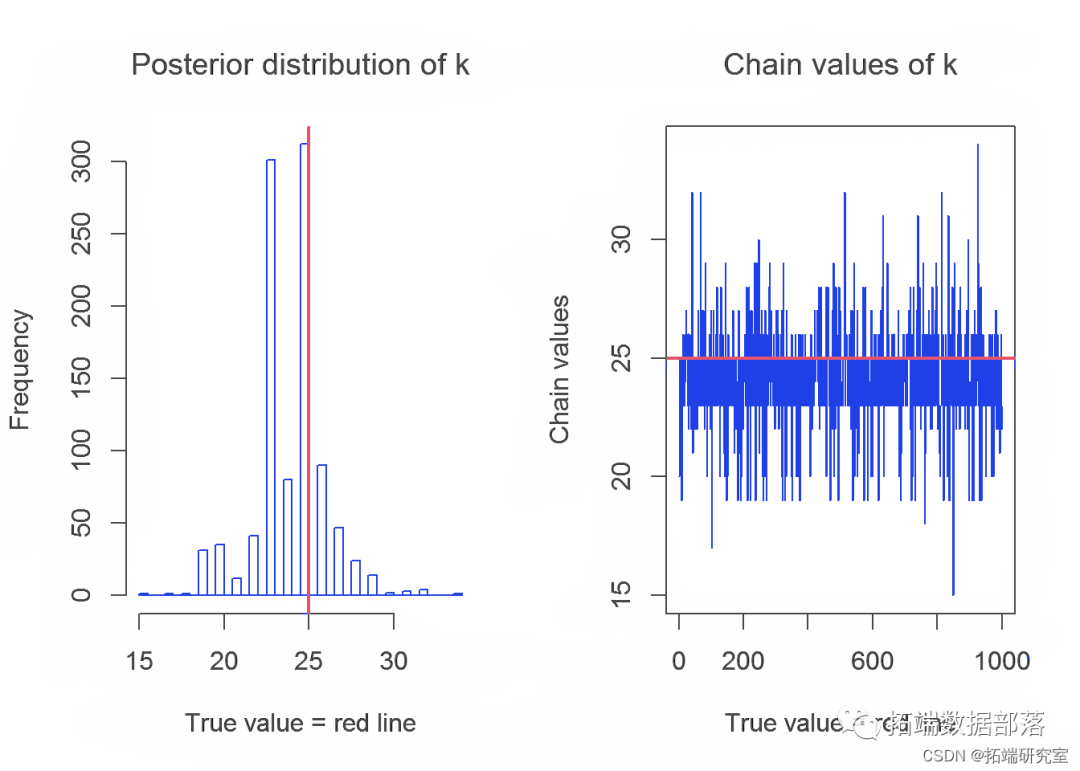
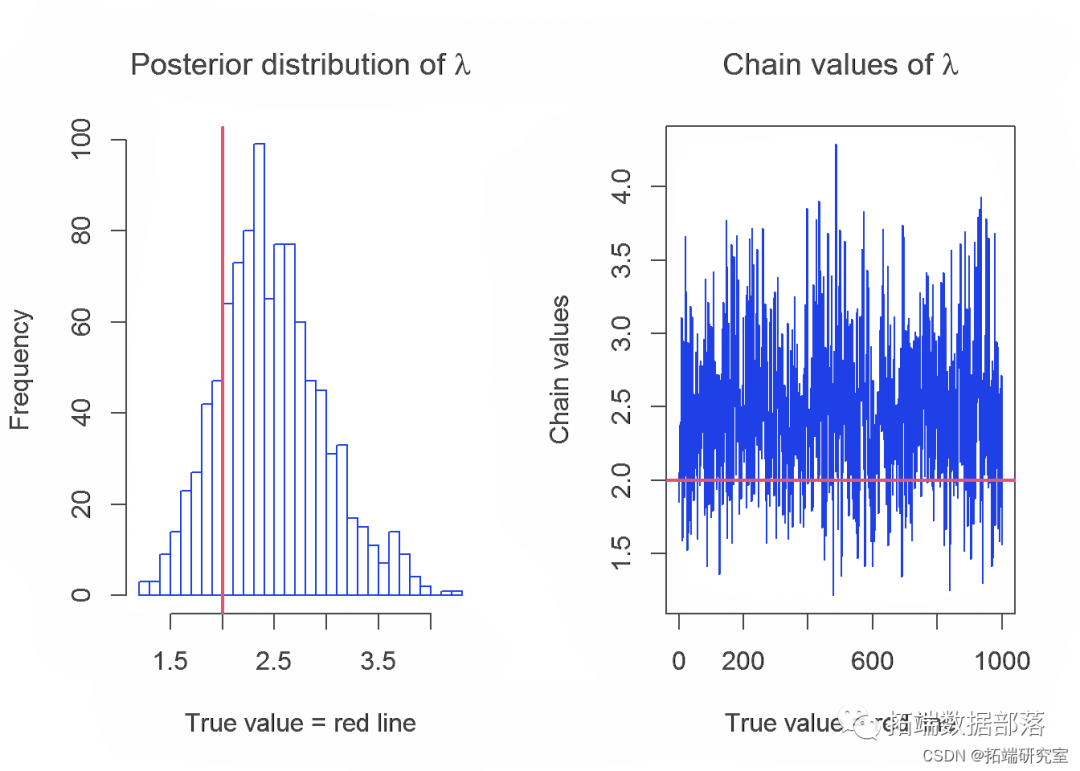
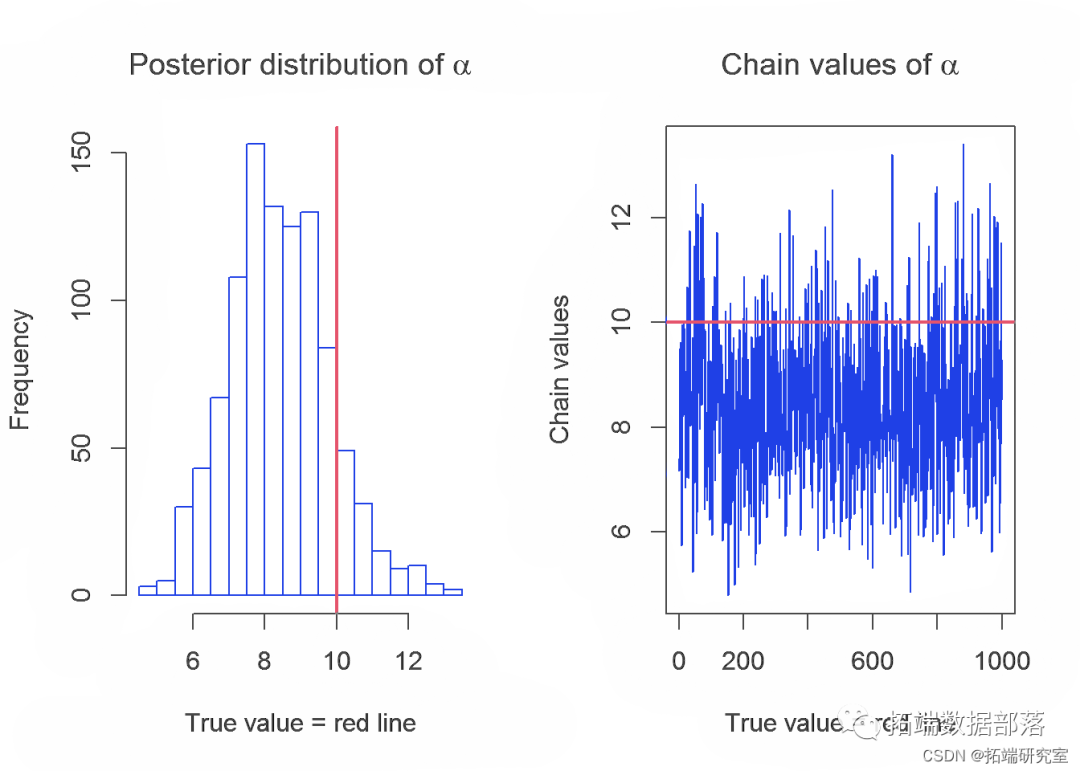
下表显示了参数的实际值和使用 Gibbs 采样器获得的估计值的平均值:
res <- c(mean(k\[-(1:bun)\]), mean(lmba\[-(1:burn)\]), mean(apa\[-(1:buI)\]))
resfil
结论
从结果中,我们可以得出结论,使用 R 中的 Gibbs 采样器获得的具有变点的指数分布对参数 k、λ 和 α 的估计值的平均值接近于参数的实际值,但是我们期望更好估计。这可能是由于选择了链的初始值或选择了 λ 和 α的先验分布。

点击文末“阅读原文”
获取全文完整资料。
本文选自《R语言贝叶斯METROPOLIS-HASTINGS GIBBS 吉布斯采样器估计变点指数分布分析泊松过程车站等待时间》。


点击标题查阅往期内容
R语言马尔可夫MCMC中的METROPOLIS HASTINGS,MH算法抽样(采样)法可视化实例
python贝叶斯随机过程:马尔可夫链Markov-Chain,MC和Metropolis-Hastings,MH采样算法可视化
Python贝叶斯推断Metropolis-Hastings(M-H)MCMC采样算法的实现
Metropolis Hastings采样和贝叶斯泊松回归Poisson模型
Matlab用BUGS马尔可夫区制转换Markov switching随机波动率模型、序列蒙特卡罗SMC、M H采样分析时间序列
R语言RSTAN MCMC:NUTS采样算法用LASSO 构建贝叶斯线性回归模型分析职业声望数据
R语言BUGS序列蒙特卡罗SMC、马尔可夫转换随机波动率SV模型、粒子滤波、Metropolis Hasting采样时间序列分析
R语言Metropolis Hastings采样和贝叶斯泊松回归Poisson模型
R语言贝叶斯MCMC:用rstan建立线性回归模型分析汽车数据和可视化诊断
R语言贝叶斯MCMC:GLM逻辑回归、Rstan线性回归、Metropolis Hastings与Gibbs采样算法实例
R语言贝叶斯Poisson泊松-正态分布模型分析职业足球比赛进球数
R语言用Rcpp加速Metropolis-Hastings抽样估计贝叶斯逻辑回归模型的参数
R语言逻辑回归、Naive Bayes贝叶斯、决策树、随机森林算法预测心脏病
R语言中贝叶斯网络(BN)、动态贝叶斯网络、线性模型分析错颌畸形数据
R语言中的block Gibbs吉布斯采样贝叶斯多元线性回归
Python贝叶斯回归分析住房负担能力数据集
R语言实现贝叶斯分位数回归、lasso和自适应lasso贝叶斯分位数回归分析
Python用PyMC3实现贝叶斯线性回归模型
R语言用WinBUGS 软件对学术能力测验建立层次(分层)贝叶斯模型
R语言Gibbs抽样的贝叶斯简单线性回归仿真分析
R语言和STAN,JAGS:用RSTAN,RJAG建立贝叶斯多元线性回归预测选举数据
R语言基于copula的贝叶斯分层混合模型的诊断准确性研究
R语言贝叶斯线性回归和多元线性回归构建工资预测模型
R语言贝叶斯推断与MCMC:实现Metropolis-Hastings 采样算法示例
R语言stan进行基于贝叶斯推断的回归模型
R语言中RStan贝叶斯层次模型分析示例
R语言使用Metropolis-Hastings采样算法自适应贝叶斯估计与可视化
R语言随机搜索变量选择SSVS估计贝叶斯向量自回归(BVAR)模型
WinBUGS对多元随机波动率模型:贝叶斯估计与模型比较
R语言实现MCMC中的Metropolis–Hastings算法与吉布斯采样
R语言贝叶斯推断与MCMC:实现Metropolis-Hastings 采样算法示例
R语言使用Metropolis-Hastings采样算法自适应贝叶斯估计与可视化
视频:R语言中的Stan概率编程MCMC采样的贝叶斯模型
R语言MCMC:Metropolis-Hastings采样用于回归的贝叶斯估计

![]()

相关文章:

R语言贝叶斯METROPOLIS-HASTINGS GIBBS 吉布斯采样器估计变点指数分布分析泊松过程车站等待时间...
原文链接:http://tecdat.cn/?p26578 指数分布是泊松过程中事件之间时间的概率分布,因此它用于预测到下一个事件的等待时间,例如,您需要在公共汽车站等待的时间,直到下一班车到了(点击文末“阅读原文”获取…...

通付盾入选2023年度“上市苗圃工程”重点企业
近日,2023年度苏州工业园区企业上市苗圃工程认定名单公示,江苏通付盾科技有限公司成功入选园区“上市苗圃工程”重点企业。 2023年第一批次苗圃企业认定结果: 企业上市苗圃工程 上市企业是衡量地方综合经济实力的重要标尺,也是区…...

SpringMVC之文件上传下载
SpringMVC是一个基于Java的Web框架,它提供了一套用于构建Web应用程序的开发模型。在SpringMVC中,文件上传和下载是常见的功能之一。 SpringMVC文件上传和下载的介绍: 介绍文件上传: 在SpringMVC中,文件上传功能可以通…...
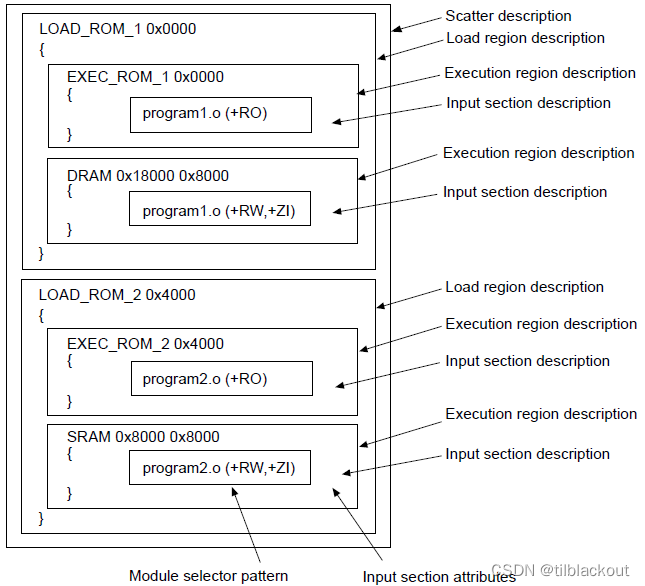
嵌入式IDE(2):KEIL中SCF分散加载链接文件详解和实例分析
在上一篇文章IAR中ICF链接文件详解和实例分析中,我通过I.MX RT1170的SDK中的内存映射关系,分析了IAR中的ICF链接文件的语法。对于MCU编程所使用的IDE来说,IAR和Keil用得比较多,所以这一篇文章就来分析一下Keil的分散文件.scf(scat…...

Linux防火墙常用操作及端口开放
Linux防火墙常用操作及端口开放 1.查看防火墙状态 firewall-cmd --state 2.开启防火墙 systemctl start firewalld.service 3.开启指定端口 firewall-cmd --zonepublic --add-port3306/tcp --permanent firewall-cmd --zonepublic --add-port6379/tcp --permanent 显示success表…...

[JAVAee]Linux上的javax.mail报错
我们把在window写的项目部署到Linux上的Tomcat时,如果发现使用不了了,该如何找到错误呢?找到报错的地方在哪呢? 在Linux环境下来到Tomcat目录下的logs目录,输入: tail -f catalina.out -n 500 tail 就是把文件的末尾几行读取到终端上,并会持续刷新 -f 循环读取 catalina.ou…...

开学季|校园迎新哪家强?VR全景来导航
九月开学迎新季,各大高校的迎新活动开展的如火如荼,随着科技的不断进步,高校为了更好的开展迎新活动,让新生们尽快熟悉新的校园和生活,会利用VR全景技术带领着新生进行校园游览,给予新生们巨大便利的同时&a…...
el-checkbox-group限制勾选数量
<!--* Description: 视频监控 页面* Author: mhf* Date: 2023-08-15 13:26:33 --> <template><div class"videoSurveillance"><el-row :gutter"24"><el-col :span"4"><div class"videoSurveillance-left&…...

【JavaScript】WebAPI入门到实战
文章目录 一、WebAPI背景知识1. 什么是WebAPI?2. 什么是API? 二、DOM基本概念三、获取元素三、事件初识1. 点击事件2. 键盘事件 四、操作元素1. 获取/修改元素内容2. 获取/修改元素属性3. 获取/修改表单元素属性4. 获取/修改样式属性 五、操作节点1. 新增…...

奥康的高尔夫鞋,圈不住投资者的心
文 | 螳螂观察 作者 | 青月 鞋服行业终于熬过了“寒冬”,2023年行业景气度开始逐步回暖。 东方财富Choice数据显示,截至8月17日,已有28家鞋帽服装类上市公司发布了2023年中期业绩预告或快报,其中,9家预增࿰…...
vue2配置环境变量并且nginx运行成功
需求:我在vue项目配置了生产环境和开发环境,之后通过proxy代理的方式把地址转发到真实的服务器地址上用于请求接口,之后把项目打包后上传到nginx上,之后接口报错404,但是本地运行是可以访问的,找了很久终于…...

Java+Swing形成GUI图像界面
一、Swing 简介 Swing 主要用来开发 GUI 程序,GUI(Graphical User Interface)即图形用户界面。Java 中针对 GUI 设计提供了丰富的类库,这些类分别位于 java.awt 和 java.swing 中,简称 AWT 和 Swing ;其中,AWT(Abstract Window Toolkit)是抽象窗口工具包,是 Java 平…...

编辑距离 -- 动规
72. 编辑距离 给出动规的两种常见实现形式:自顶向下、自底向上,前者一般借助递归函数备忘录实现,后者通常基于dp数组实现。 class MinDistance:"""72. 编辑距离https://leetcode.cn/problems/edit-distance/""&quo…...

douyin【商品抢购js脚本】
文章目录 前言订阅须知知识点源码前言 脚本主要用来实现抢购douyin商城、直播间秒杀商品等一系列商品 订阅须知 订阅后,只提供js源代码,不提供教学,请根据源码自行抓包知识点 1、在查询串插入一个固定的键rstr 2、对查询串进行按键排序并取值,对空格和+进行转义为a …...
常见Web安全技术总结!474页Web安全从入门到精通(附PDF)
Web安全范围比较大,知识点比较杂,很多朋友都无从下手,这不可怕,可怕的是乱下手,其实往往基础才是决定你是否能走远的关键。 为了帮助大家入门网安,给大家推荐一份《新手Web安全入门到精通》,共…...

Prometheus 监控指南:如何可靠地记录数字时间序列数据
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🐅🐾猫头虎建议程序员必备技术栈一览表📖: 🛠️ 全栈技术 Full Stack: 📚…...
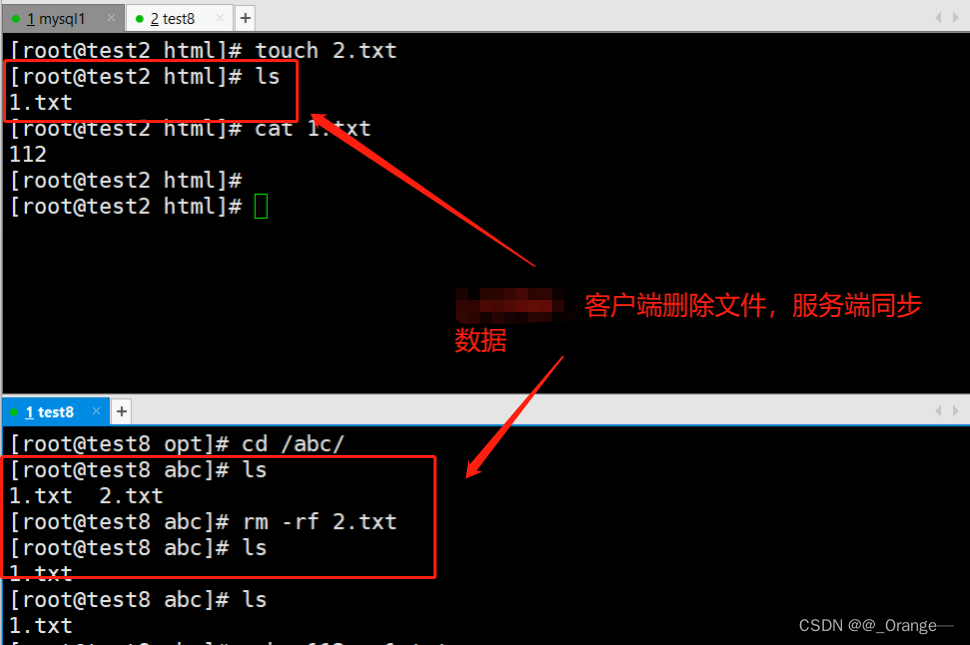
rsync远程同步+inotify监控
目录 一、Rsync 简介 1、rsync是什么 2、备份的方式 3、rsync同步方式 4、常用rsync命令 5、配置源的两种表达方法 二、rsync实验 1、本地复制 编辑编辑 2、异地复制 2.1 rsync服务器配置 2.2 rsync客户端配置 2.2.1 普通同步 2.2.2 免密同步 2.2.3 --delet…...

【面试经典150 | 数组】移除元素
文章目录 写在前面Tag题目来源题目解读解题思路方法一:原地操作 写在最后 写在前面 本专栏专注于分析与讲解【面试经典150】算法,两到三天更新一篇文章,欢迎催更…… 专栏内容以分析题目为主,并附带一些对于本题涉及到的数据结构等…...

玩转Mysql系列 - 第21篇:什么是索引?
这是Mysql系列第21篇。 本文开始连续3篇详解mysql索引: 第1篇来说说什么是索引? 第2篇详解Mysql中索引的原理 第3篇结合索引详解关键字explain 本文为索引第一篇:我们来了解一下什么是索引? 路人在搞计算机之前,…...

预处理指令
// The include directive instructs the preprocessor to paste the text of the given file into the current file. // 粘贴指定文件的内容 #include // 定义宏PI #define PI 3.1415926 // 取消定义PI #undef PI条件编译(Conditional Compilation) // 检查xxx是否已被定义为…...

LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器的上位机配置操作说明
LBE-LEX系列工业语音播放器|预警播报器|喇叭蜂鸣器专为工业环境精心打造,完美适配AGV和无人叉车。同时,集成以太网与语音合成技术,为各类高级系统(如MES、调度系统、库位管理、立库等)提供高效便捷的语音交互体验。 L…...

MPNet:旋转机械轻量化故障诊断模型详解python代码复现
目录 一、问题背景与挑战 二、MPNet核心架构 2.1 多分支特征融合模块(MBFM) 2.2 残差注意力金字塔模块(RAPM) 2.2.1 空间金字塔注意力(SPA) 2.2.2 金字塔残差块(PRBlock) 2.3 分类器设计 三、关键技术突破 3.1 多尺度特征融合 3.2 轻量化设计策略 3.3 抗噪声…...

docker详细操作--未完待续
docker介绍 docker官网: Docker:加速容器应用程序开发 harbor官网:Harbor - Harbor 中文 使用docker加速器: Docker镜像极速下载服务 - 毫秒镜像 是什么 Docker 是一种开源的容器化平台,用于将应用程序及其依赖项(如库、运行时环…...

SpringBoot+uniapp 的 Champion 俱乐部微信小程序设计与实现,论文初版实现
摘要 本论文旨在设计并实现基于 SpringBoot 和 uniapp 的 Champion 俱乐部微信小程序,以满足俱乐部线上活动推广、会员管理、社交互动等需求。通过 SpringBoot 搭建后端服务,提供稳定高效的数据处理与业务逻辑支持;利用 uniapp 实现跨平台前…...

C++ 求圆面积的程序(Program to find area of a circle)
给定半径r,求圆的面积。圆的面积应精确到小数点后5位。 例子: 输入:r 5 输出:78.53982 解释:由于面积 PI * r * r 3.14159265358979323846 * 5 * 5 78.53982,因为我们只保留小数点后 5 位数字。 输…...

HTML前端开发:JavaScript 常用事件详解
作为前端开发的核心,JavaScript 事件是用户与网页交互的基础。以下是常见事件的详细说明和用法示例: 1. onclick - 点击事件 当元素被单击时触发(左键点击) button.onclick function() {alert("按钮被点击了!&…...

【学习笔记】深入理解Java虚拟机学习笔记——第4章 虚拟机性能监控,故障处理工具
第2章 虚拟机性能监控,故障处理工具 4.1 概述 略 4.2 基础故障处理工具 4.2.1 jps:虚拟机进程状况工具 命令:jps [options] [hostid] 功能:本地虚拟机进程显示进程ID(与ps相同),可同时显示主类&#x…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

NPOI Excel用OLE对象的形式插入文件附件以及插入图片
static void Main(string[] args) {XlsWithObjData();Console.WriteLine("输出完成"); }static void XlsWithObjData() {// 创建工作簿和单元格,只有HSSFWorkbook,XSSFWorkbook不可以HSSFWorkbook workbook new HSSFWorkbook();HSSFSheet sheet (HSSFSheet)workboo…...

C# 表达式和运算符(求值顺序)
求值顺序 表达式可以由许多嵌套的子表达式构成。子表达式的求值顺序可以使表达式的最终值发生 变化。 例如,已知表达式3*52,依照子表达式的求值顺序,有两种可能的结果,如图9-3所示。 如果乘法先执行,结果是17。如果5…...
