二进制、数位dp:0912T3
考虑题目转化,二进制下满足 i ⊆ j , ( i + x ) ⊆ ( j + y ) i\subseteq j,(i+x)\subseteq (j+y) i⊆j,(i+x)⊆(j+y)
这显然是个数位dp形式
考虑枚举每一位与进位, d p k , p 1 , p 2 dp_{k,p_1,p_2} dpk,p1,p2 表示第 k − 1 k-1 k−1 位向第 k k k 位,分别进位 p 1 , p 2 p_1,p_2 p1,p2 的方案数
考虑当前 ( i , j ) (i,j) (i,j) 二进制下分别为 q 1 , q 2 q_1,q_2 q1,q2,则 ( i + x , j + y ) = ( p 1 + q 1 + x i , p 2 + q 2 + y i ) = ( n 1 , n 2 ) (i+x,j+y)=(p_1+q_1+x_i,p_2+q_2+y_i)=(n_1,n_2) (i+x,j+y)=(p1+q1+xi,p2+q2+yi)=(n1,n2)
必须满足 q 1 ⊆ q 2 , n 1 & 1 ⊆ n 2 & 1 q1\subseteq q2,n1\&1\subseteq n2\&1 q1⊆q2,n1&1⊆n2&1,由 d p ( i + 1 , n 1 2 , n 2 2 ) dp(i+1,\frac{n_1}2,\frac{n_2}2) dp(i+1,2n1,2n2) 转移过来
综上:
d p ( k , i , j ) = ∑ q 1 ⊆ q 2 , n 1 = p 1 + q 1 + x i , n 2 = p 2 + q 2 + y i [ n 1 & 1 ⊆ n 2 & 1 ] d p ( i + 1 , n 1 2 , n 2 2 ) \Large dp(k,i,j)=\sum_{q1\subseteq q2,n1=p1+q1+x_i,n2=p2+q2+y_i}[n1\&1\subseteq n2\&1]dp(i+1,\frac{n_1}2,\frac{n_2}2) dp(k,i,j)=q1⊆q2,n1=p1+q1+xi,n2=p2+q2+yi∑[n1&1⊆n2&1]dp(i+1,2n1,2n2)
dp[n][0][0].a[1]=1;
for(i=n-1; i>=0; --i) {for(p1=0; p1<=1; ++p1) for(p2=0; p2<=1; ++p2) {for(q1=0; q1<=1; ++q1) for(q2=q1; q2<=1; ++q2) {n1=p1+q1+x[i]; n2=p2+q2+y[i]; if(n1%2>n2%2) continue; dp[i][p1][p2]=dp[i][p1][p2]+dp[i+1][n1/2][n2/2]; }}}
dp[0][0][0].print();
相关文章:

二进制、数位dp:0912T3
考虑题目转化,二进制下满足 i ⊆ j , ( i x ) ⊆ ( j y ) i\subseteq j,(ix)\subseteq (jy) i⊆j,(ix)⊆(jy) 这显然是个数位dp形式 考虑枚举每一位与进位, d p k , p 1 , p 2 dp_{k,p_1,p_2} dpk,p1,p2 表示第 k − 1 k-1 k−1 位向第 k k…...
Java基于SpringBoot+Vue的 4S店车辆管理系统
博主介绍:✌程序员徐师兄、7年大厂程序员经历。全网粉丝30W,Csdn博客专家、掘金/华为云/阿里云/InfoQ等平台优质作者、专注于Java技术领域和毕业项目实战✌ 文章目录 1 简介2 技术栈3 功能总览4 系统设计4.1 系统设计主要功能4.2 数据库设计4.2.1 数据库设计规范4.2…...
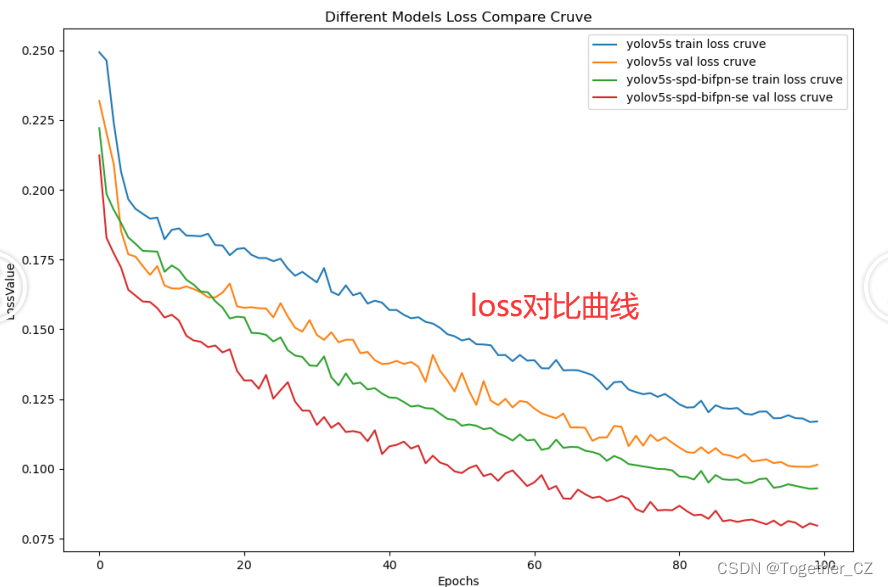
助力智能化公路养护,基于YOLOv5s集成SPD-BIFPN-SE开发构建公路开裂检测识别系统
在前文中我们尝试构建了在隧道、涵洞尝尽下的自动智能化养护巡查相关的模型,进行了实地测试评估,感兴趣的话可以自行移步阅读即可: 《基于轻量级YOLOv5s开发构建隧道基建裂痕、脱落等缺陷问题检测系统》 本文的想法是相近的,核心…...

C++--day5
实现一个图形类(Shape),包含受保护成员属性:周长、面积, 公共成员函数:特殊成员函数书写 定义一个圆形类(Circle),继承自图形类,包含私有属性:半…...
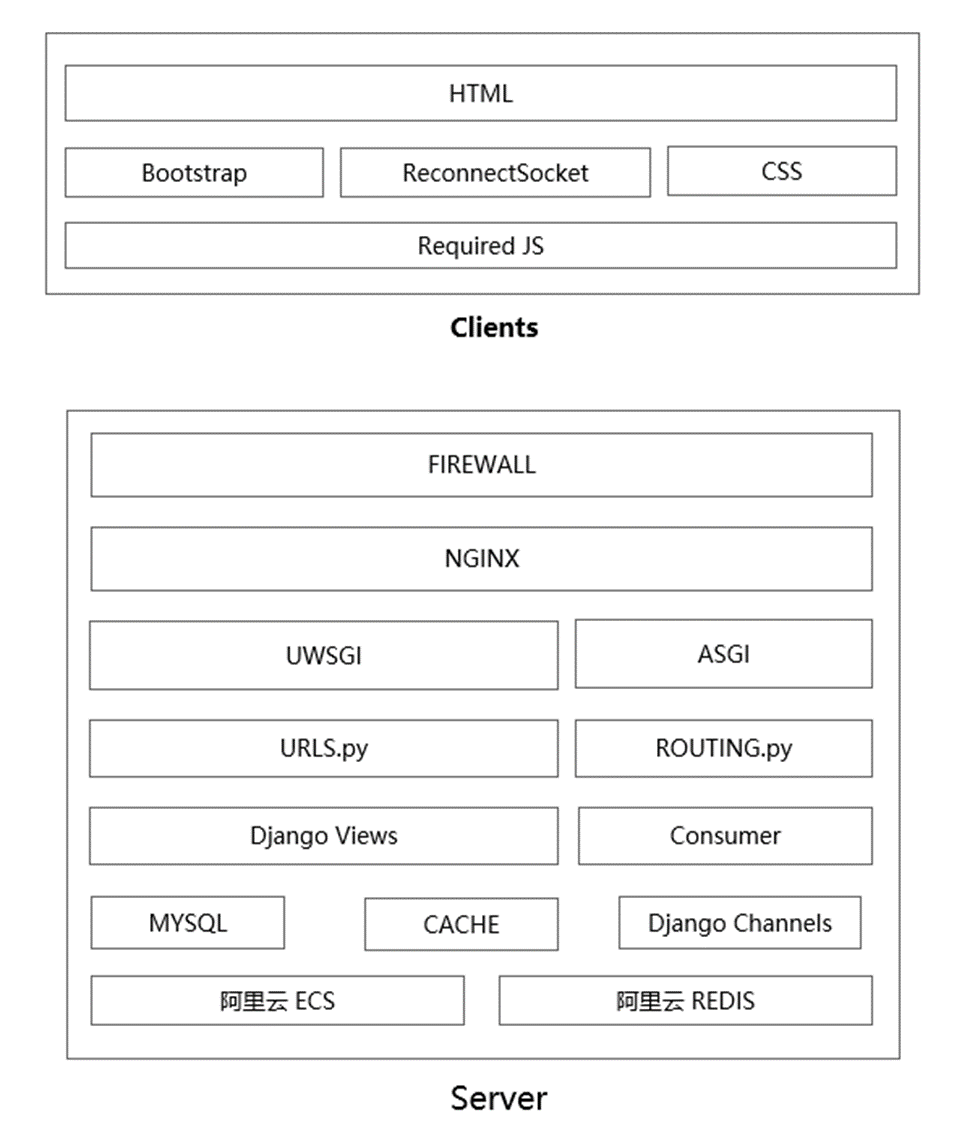
Django应用部署实战:从开发到生产,全程解析
部署架构图 版本说明 Centos 7.4 Python 3.6.4 Django 2.0.2 Channels 2.0.0 MySql 5.7 uWSGI Nginx 1.12.2 部署前 1、更新系统环境 yum install epel-release 2、安装所有的开发工具包 yum groupinstall -y “Development tools” 一、安装python 3.6.4 1、下载 cd /usr/…...
群晖NAS如何在内网部署HTTPS服务让浏览器信任证书
前言 最近在折腾内部部署Web服务。通过Vue实现一个H5的内部的管理服务。但在实际部署过程中由于种种原因,必须部署成Https服务。但在部署成Https服务后,由于没有HTTPS证书,每次进入页面都会被浏览器拦截。使用起来非常不便。于是开始各种Goo…...
crAPI靶场学习记录
靶场搭建 [靶场下载地址](我fork了一份) docker安装,笔者是用的wsldocker. [lab0:**初始账户 **] 注册一个账户,邮箱为[APIqq.com],密码为Admin123 登陆后访问对应IP的8025端口,接收邮件获取车辆信息。 [lab1:**访问其它用户车…...

知识图谱实战应用28-基于py2neo的ICD-11疾病分类的知识图谱的查询与问答实战应用
大家好,我是微学AI,今天给大家介绍一下知识图谱实战应用28-基于py2neo的ICD-11疾病分类的知识图谱的查询与问答实战应用。使用基于py2neo的ICD-11疾病分类知识图谱,我们能够像探索一座生物医学宇宙般,穿梭在各种疾病之间。这个神奇的图谱可以帮助我们揭示各种疾病之间复杂而…...
20.Xaml GroupBox控件 ---->带标题的内容控件
1.运行效果 2.运行源码 a.Xaml源码 <Window x:Class="testView.MainWindow"xmlns="http://schemas.microsoft.com/winfx/2006/xaml/presentation"xmlns:x="http://schemas.microsoft.com/winfx/2006/xaml"xmlns:d="http://schemas.mic…...

基于CycleGAN的山水风格画迁移
基于CycleGAN的山水风格画迁移 1、简介 1.1 研究背景及意义 绘画是人类重要的一种艺术形式,其中中国的山水画源远流长,具有丰富的美学内涵,沉淀着中国人的情思。游山玩水的大陆文化意识,以山为德、水为性的内在修为意识&#x…...

@Cacheable 注解
1. 功能说明 Cacheable 注解在方法上,表示该方法的返回结果是可以缓存的。也就是说,该方法的返回结果会放在缓存中,以便于以后使用相同的参数调用该方法时,会返回缓存中的值,而不会实际执行该方法。 注意,这…...
vue3+ts项目打包后的本地访问
注意:打包之后不可直接点击html访问,需要给项目安装本地服务! 1、安装servenpm i -g serve 2、打包项目npm run build 生成dist文件夹 3、本地访问serve dist 运行service dist之后的控制台 可复制下方的地址运行打包后的项目,运行…...

探索程序员需要掌握的算法?
文章目录 一:引言二:常见算法介绍三:重点算法总结 🎉欢迎来到数据结构学习专栏~探索程序员需要掌握的算法? ☆* o(≧▽≦)o *☆嗨~我是IT陈寒🍹✨博客主页:IT陈寒的博客🎈该系列文章…...
性能测试 —— Jmeter定时器
固定定时器 如果你需要让每个线程在请求之前按相同的指定时间停顿,那么可以使用这个定时器;需要注意的是,固定定时器的延时不会计入单个sampler的响应时间,但会计入事务控制器的时间 1、使用固定定时器位置在http请求中…...

mp4视频太大怎么压缩?几种常见压缩方法
mp4视频太大怎么压缩?科技的飞速发展使得视频成为人们生活中不可或缺的一部分。然而,随着视频质量的不断提高,视频文件的大小也与日俱增,给我们的存储和传输带来了巨大的挑战和困扰。特别是MP4格式的视频,由于其出色的…...

论文复制ChatGPT按钮被发表,撤回后再曝多个类似案例;Midjourney 生成大师级的人像
🦉 AI新闻 🚀 论文复制ChatGPT按钮被发表,撤回后再曝多个类似案例 摘要:一篇物理论文复制了ChatGPT按钮内容,经过两个月同行评审并在杂志上发表。这一现象被知名打假人发现后,发表商决定撤回该论文。此外…...
Python自动化测试 史上最全的进阶教程
Python自动化测试就是把以前人为测试转化为机器测试的一种过程。自动化测试是一种比手工测试更快获得故障反馈的方法。 随着时代的变革,也许在未来测试这个职位的需求会越来越少甚至消失,但是每一个组织,每一个客户对软件质量的要求是永远不…...

centos pip失效
在 CentOS 上安装和配置 pip3 可能需要以下步骤: 确保 Python 3 已正确安装:请确保您已经正确地安装了 Python 3。在 CentOS 上,Python 3 可能默认安装在 /usr/bin/python3 路径下。您可以通过运行以下命令来验证 Python 3 是否正确安装&…...
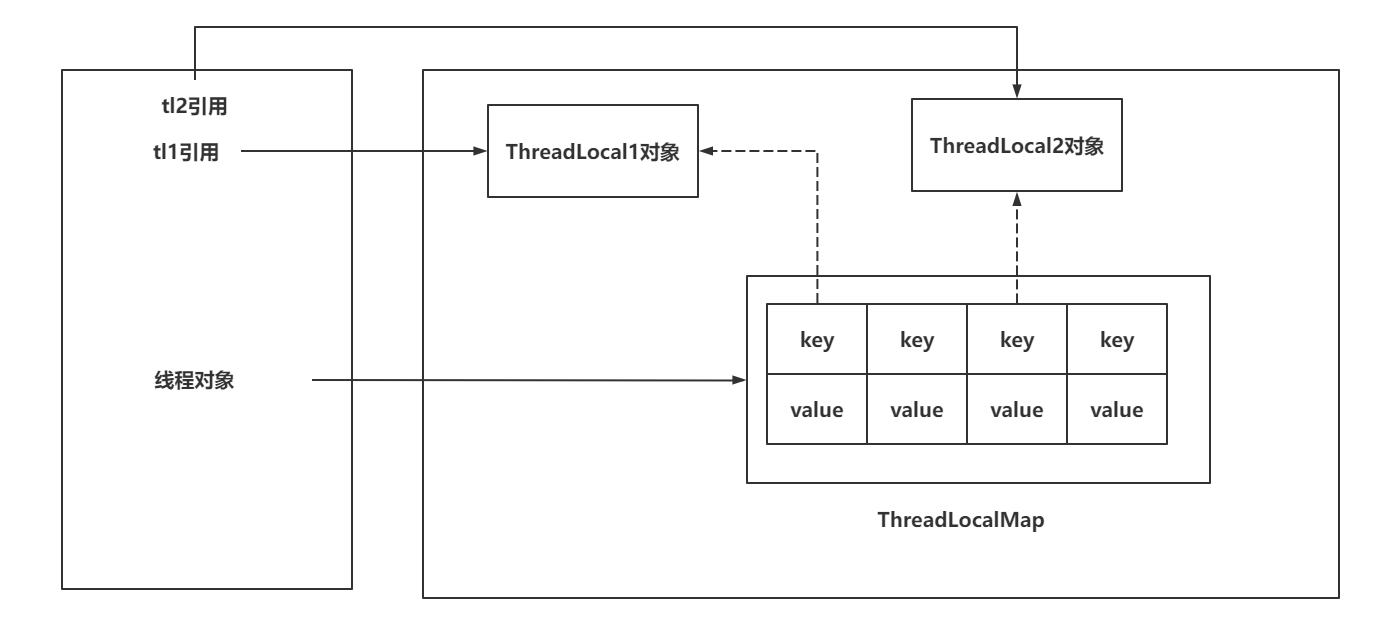
Java——》ThreadLocal
推荐链接: 总结——》【Java】 总结——》【Mysql】 总结——》【Redis】 总结——》【Kafka】 总结——》【Spring】 总结——》【SpringBoot】 总结——》【MyBatis、MyBatis-Plus】 总结——》【Linux】 总结——》【MongoD…...

如何做好利益相关方的期望管理?
利益相关方对项目而言非常重要,有效管理利益相关方的期望可以帮助项目团队更好地满足利益相关方的需求,助于建立良好的合作伙伴关系,提高项目的可持续性和成功率。 如果项目团队无法满足利益相关方的需求,可能会引发冲突、争议或其…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

大话软工笔记—需求分析概述
需求分析,就是要对需求调研收集到的资料信息逐个地进行拆分、研究,从大量的不确定“需求”中确定出哪些需求最终要转换为确定的“功能需求”。 需求分析的作用非常重要,后续设计的依据主要来自于需求分析的成果,包括: 项目的目的…...

Qt/C++开发监控GB28181系统/取流协议/同时支持udp/tcp被动/tcp主动
一、前言说明 在2011版本的gb28181协议中,拉取视频流只要求udp方式,从2016开始要求新增支持tcp被动和tcp主动两种方式,udp理论上会丢包的,所以实际使用过程可能会出现画面花屏的情况,而tcp肯定不丢包,起码…...

uni-app学习笔记二十二---使用vite.config.js全局导入常用依赖
在前面的练习中,每个页面需要使用ref,onShow等生命周期钩子函数时都需要像下面这样导入 import {onMounted, ref} from "vue" 如果不想每个页面都导入,需要使用node.js命令npm安装unplugin-auto-import npm install unplugin-au…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...
)
GitHub 趋势日报 (2025年06月08日)
📊 由 TrendForge 系统生成 | 🌐 https://trendforge.devlive.org/ 🌐 本日报中的项目描述已自动翻译为中文 📈 今日获星趋势图 今日获星趋势图 884 cognee 566 dify 414 HumanSystemOptimization 414 omni-tools 321 note-gen …...

CRMEB 框架中 PHP 上传扩展开发:涵盖本地上传及阿里云 OSS、腾讯云 COS、七牛云
目前已有本地上传、阿里云OSS上传、腾讯云COS上传、七牛云上传扩展 扩展入口文件 文件目录 crmeb\services\upload\Upload.php namespace crmeb\services\upload;use crmeb\basic\BaseManager; use think\facade\Config;/*** Class Upload* package crmeb\services\upload* …...

Android 之 kotlin 语言学习笔记三(Kotlin-Java 互操作)
参考官方文档:https://developer.android.google.cn/kotlin/interop?hlzh-cn 一、Java(供 Kotlin 使用) 1、不得使用硬关键字 不要使用 Kotlin 的任何硬关键字作为方法的名称 或字段。允许使用 Kotlin 的软关键字、修饰符关键字和特殊标识…...

【碎碎念】宝可梦 Mesh GO : 基于MESH网络的口袋妖怪 宝可梦GO游戏自组网系统
目录 游戏说明《宝可梦 Mesh GO》 —— 局域宝可梦探索Pokmon GO 类游戏核心理念应用场景Mesh 特性 宝可梦玩法融合设计游戏构想要素1. 地图探索(基于物理空间 广播范围)2. 野生宝可梦生成与广播3. 对战系统4. 道具与通信5. 延伸玩法 安全性设计 技术选…...
