不定积分的概念和性质
目录
原函数
不定积分
不定积分的几何意义
原函数的存在定理
不定积分的性质

不定积分是微积分的一个关键部分,它涉及到一个函数的不定积分的计算。不定积分可以理解为求一个函数的原函数,也被称为反导数。原函数是一个函数,使得该函数的导数等于被积函数。不定积分的基本性质包括:
- 函数和的不定积分等于各个函数的不定积分的和。
- 在求不定积分时,被积函数中的常数因子可以提到积分号外面来。
原函数
不定积分是微积分的一个关键部分,它涉及到一个函数的不定积分的计算。不定积分可以理解为求一个函数的原函数,也被称为反导数。原函数是一个函数,使得该函数的导数等于被积函数。
不定积分的基本性质包括:
- 函数和的不定积分等于各个函数的不定积分的和。
- 在求不定积分时,被积函数中的常数因子可以提到积分号外面来。
例如,对于函数f(x) = x^2,它的不定积分是x^3/3 + C,其中C是任意常数。
不定积分
不定积分是微积分的一个关键部分,它涉及到一个函数的不定积分的计算。不定积分可以理解为求一个函数的原函数,也被称为反导数。原函数是一个函数,使得该函数的导数等于被积函数。
不定积分的基本性质包括:
- 函数和的不定积分等于各个函数的不定积分的和。
- 在求不定积分时,被积函数中的常数因子可以提到积分号外面来。
例如,对于函数f(x) = x^2,它的不定积分是x^3/3 + C,其中C是任意常数。
不定积分的几何意义
不定积分的几何意义是曲线。
若F是f的一个原函数,则称y=F(x)的图像为f的一条积分曲线。
f的不定积分在几何上表示f的某一积分曲线沿着纵轴方向任意平移,所得到的一切积分曲线所组成的曲线族。
若在每一条积分曲线横坐标相同的点处作切线,则这些切线是相互平行的。
在求原函数的具体问题中,往往先求出全体原函数F(x)+C,然后带入特殊点或已知点,求出常数C,进而得到要求的那条积分曲线。

原函数的存在定理
原函数存在定理是指如果一个函数f(x)在区间[a,b]上连续,那么在该区间上存在原函数。这个定理是充分条件,但不是必要条件。即,如果一个函数有原函数,那么这个函数一定是连续的,但连续的函数不一定有原函数。
这个定理对于初等函数在其定义的区间上都是成立的,因为初等函数在其定义的区间上都是连续的,所以它们都有原函数。需要注意的是,初等函数的导数一定是初等函数,但初等函数的原函数不一定是初等函数。
不定积分的性质
不定积分是一个微积分中的重要概念,它具有以下性质:
- 线性性质:不定积分具有线性性质,即两个函数的线性组合的积分等于各自积分的线性组合。数学表达式为:∫(af(x) + bg(x))dx = a∫f(x)dx + b∫g(x)dx,其中a和b为常数,f(x)和g(x)为可积函数。
- 常数倍性质:不定积分的常数倍性质指的是将函数乘以一个常数后,其积分等于原积分与常数的乘积。数学表达式为:∫cf(x)dx = c∫f(x)dx,其中c为常数,f(x)为可积函数。
- 加法性质:不定积分的加法性质表明两个函数的和的积分等于各自积分的和。数学表达式为:∫(f(x) + g(x))dx = ∫f(x)dx + ∫g(x)dx,其中f(x)和g(x)为可积函数。
- 分部积分:分部积分是一种求解复合函数积分的方法,适用于两个函数的乘积的积分。分部积分公式为:∫u(x)v'(x)dx = u(x)v(x) - ∫u'(x)v(x)dx,其中u(x)和v(x)为可微函数,u'(x)和v'(x)分别表示它们的导数。
- 换元法:换元法是一种求解复杂积分的方法,通过将积分变量替换为另一个变量来简化积分问题。这个方法可以分为直接换元法和反向换元法。通过了解不定积分的性质,我们可以更好地理解和应用微积分的知识,从而更深入地解决实际问题。
不定积分是微积分中的重要概念,它是求函数的原函数的过程。通过对这个过程的理解和掌握,我们可以更好地理解微积分的应用,从而更好地解决实际问题。
相关文章:

不定积分的概念和性质
目录 原函数 不定积分 不定积分的几何意义 原函数的存在定理 不定积分的性质 不定积分是微积分的一个关键部分,它涉及到一个函数的不定积分的计算。不定积分可以理解为求一个函数的原函数,也被称为反导数。原函数是一个函数,使得该函数的…...

远程访问服务器JupyterLab的配置方法
远程访问服务器JupyterLab的配置方法 环境及工具注意 基本步骤生成密码生成并修改配置文件*错误:jupyter localhost 已拒绝连接*后台运行jupyter后台关闭 其实就是在服务器运行JupyterLab,然后在本地浏览器访问 环境及工具 服务器:Ubuntu 1…...
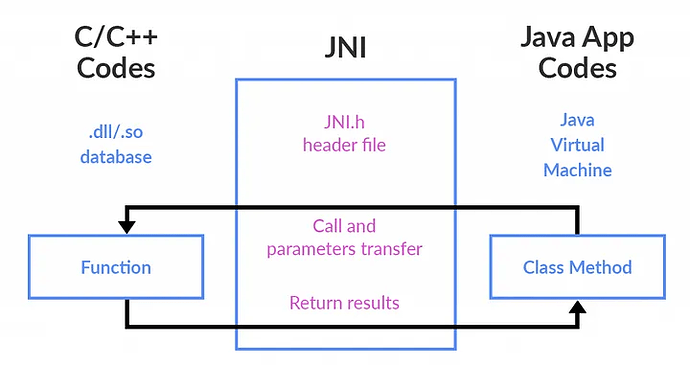
Java native 关键字
如你在看 JDK 的源代码的时候,大概率会看到很多方法使用了 native 关键字。 下面是 String 对象 JDK 中的源代码,就带有了一个 native 关键字。 native 是干什么用的 简单来说就是 Java 的 native 方法的实现不是用 Java 实现的,可能在其他…...
【线性代数】沉浸式线性代数在线学习网站
地址:http://immersivemath.com/ila/index.html 这是全球第一本带交互式图形的线性代数教材,作者是 J. Strm, K. strm, and T. Akenine-Mller。 全书一共十章,各章节内容如下: 接下来我将对各章节进行简单的总结,另外…...

Kotlin中特性、数据类、伴生对象、顶层函数
Kotlin中的函数参数和属性声明 在 Kotlin 中,函数参数和属性有不同的声明方式和行为。这些特性使得 Kotlin 代码更加安全、易于理解和维护。 函数参数的只读性 fun sum(a: Int, b: Int): Int {var modifiedA aif (modifiedA > 0) {modifiedA 1}//三元表达式v…...

《PostgreSQL物化视图:创建、维护与应用》
🌷🍁 博主猫头虎(🐅🐾)带您 Go to New World✨🍁 🐅🐾猫头虎建议程序员必备技术栈一览表📖: 🛠️ 全栈技术 Full Stack: 📚…...

shell脚本之test命令
shell脚本之test命令 数值比较:2. 字符串比较:3. 文件测试:4. 逻辑操作:5. 其他测试: test命令在Shell脚本中用于进行条件测试和条件判断。它用于检查文件、字符串和数值的各种条件,并返回一个状态码&#…...

JAVA设计模式8:装饰模式,动态地将责任附加到对象上,扩展对象的功能
作者主页:Designer 小郑 作者简介:3年JAVA全栈开发经验,专注JAVA技术、系统定制、远程指导,致力于企业数字化转型,CSDN博客专家,阿里云社区专家博主,蓝桥云课讲师。 目录 一、什么是装饰模式二、…...

Linux学习之MySQL备份
xtrabackup资源下载 完全备份与恢复 # 1.物理备份与恢复 # 冷备份,需停止数据库服务 适合线下服务器。 [rootmysql50 ~]# systemctl stop mysqld [rootmysql50 ~]# mkdir /bakdir [rootmysql50 ~]# cp -r /var/lib/mysql /bakdir/mysql.bak [rootmysql50 ~]# cd /…...
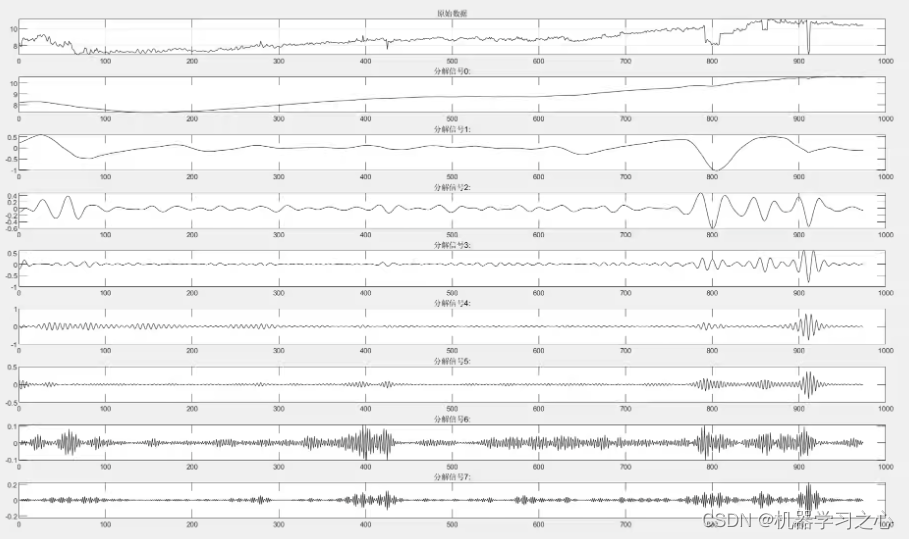
时序分解 | MATLAB实现北方苍鹰优化算法NGO优化VMD信号分量可视化
时序分解 | MATLAB实现北方苍鹰优化算法NGO优化VMD信号分量可视化 目录 时序分解 | MATLAB实现北方苍鹰优化算法NGO优化VMD信号分量可视化效果一览基本介绍程序设计参考资料 效果一览 基本介绍 北方苍鹰优化算法NGO优化VMD,对其分解层数,惩罚因子数做优化…...
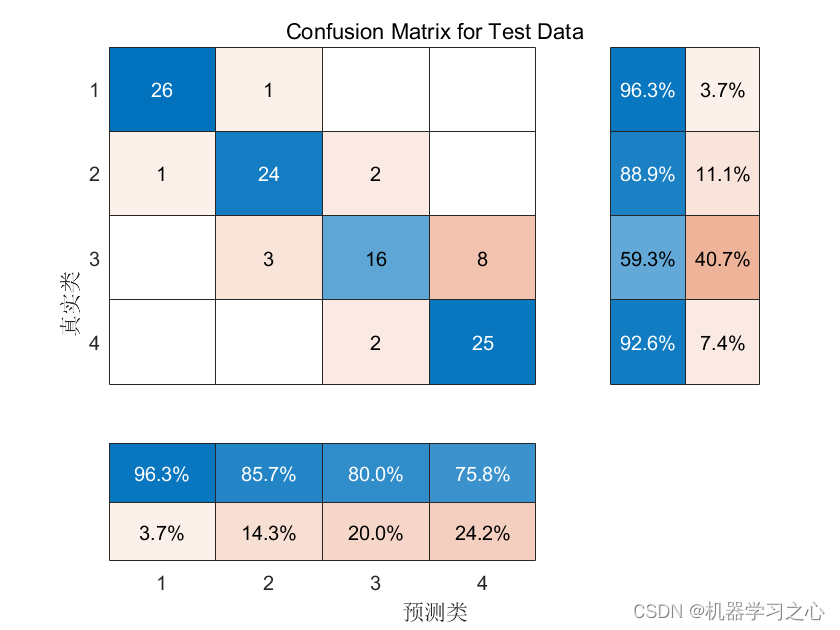
分类预测 | Matlab实现RBF-Adaboost多特征分类预测
分类预测 | Matlab实现RBF-Adaboost多特征分类预测 目录 分类预测 | Matlab实现RBF-Adaboost多特征分类预测效果一览基本介绍研究内容程序设计参考资料 效果一览 基本介绍 1.Matlab实现基于RBF-Adaboost数据分类预测(Matlab完整程序和数据) 2.多特征输入…...

【Java代码规范】阿里编码规约 VS CheckStyle
全文速览: 1、关于代码编码质量2、如何小成本有效管理企业内的编码规范 2.1 阿里编码规约IDE插件2.2 CheckStyle IDE插件 3、如何在代码提交中检验规范 3.1 阿里编码规约配置git precommit check3.2 CheckStyle配置git precommit check3.3 实践 1、关于代码编码质…...
iPhone苹果15手机圆点怎么设置让屏幕上显示出来圆形图标?
iPhone苹果15手机圆点怎么设置让屏幕上显示出来圆形图标? 1、在iPhone苹果手机上找到「设置」并点击打开; 2、在苹果iPhone设置内找到「辅助功能」并点击打开; 3、在苹果iPhone手机辅助功能内的动作交互内找到「触控」并点击打开;…...

kibana报错内存溢出问题解决
一、背景: kibana内存溢出,进程被kill掉,导致前端页面访问不到。 报错内容 二、报错原因: 发现是前端 js 报的内存 oom 异常,通过网上资料发现node.js 的默认内存大小为1.4G Node 中通过 JavaScript 使用内存时只能…...

【C语法】1124循环结构
#include <stdio.h> int main(){ //输入一个数。倒叙输出各个位上的数。 //123456 6 5 4 3 2 1 // 1输出个位上的数 %10 // 2将这个数去掉个位上的数。 / 10 // 3当这个数最后变成0时结束 int a 0; printf("请输入一个正整数:"); scanf…...

在PHP8中向数组添加元素-PHP8知识详解
在php8中向数组添加元素有多种方法,在这里主要讲解几个常用的方法:使用方括号[]添加元素、使用array_unshift()函数,向数组的头部添加元素、使用array_push()函数,向数组的尾部添加元素、使用array_splice()函数添加元素。 1、使用…...
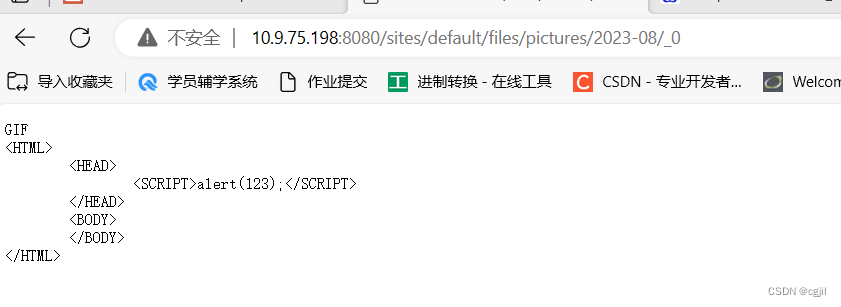
Drupal __ 8.5.0 __ XSS文件上传 __CVE-2019-6341
Drupal __ 8.5.0 __ XSS文件上传 __CVE-2019-6341 说明内容漏洞编号CVE-2019-6341漏洞名称Drupal XSS漏洞漏洞评级中危影响范围在7.65之前的Drupal 7版本中; 8.6.13之前的Drupal 8.6版本; 8.5.14之前的Drupal 8.5版本。漏洞描述Drupal诞生于2000年,是一…...
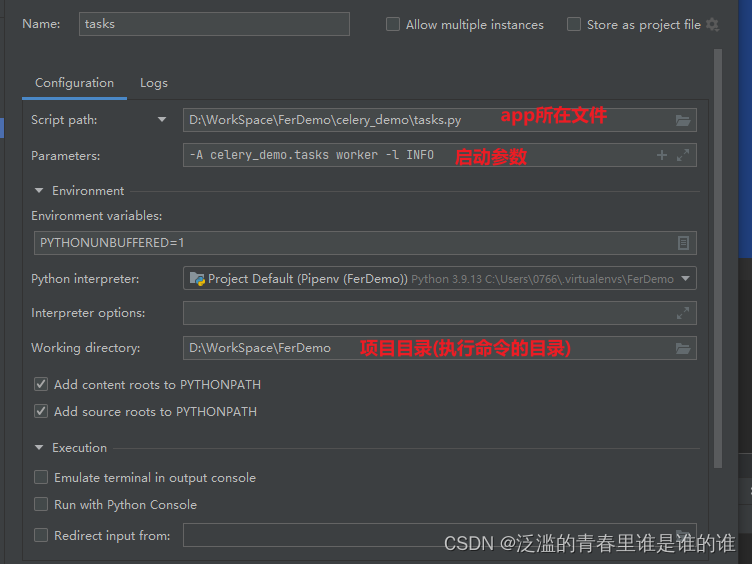
Pycharm中配置Celery启动
Pycharm中配置Celery启动 前置条件 目录结构 ----FerDemo --------celery_demo ------------tasks.py tasks.py文件代码 import sys import time from celery import Celeryapp Celery(demo,backendredis://:password127.0.0.1/0,brokerredis://:password127.0.0.1/1,broker…...

Jmeter —— 常用的几种断言方法(基本用法)
在使用JMeter进行性能测试或者接口自动化测试工作中,经常会用到的一个功能,就是断言,断言相当于检查点,它是用来判断系统返回的响应结果是否正确,以此帮我们判断测试是否通过,本文 主要介绍几种常用的断言&…...

mybatis bean属性识别丢失【NoSuchPropertyException】
背景 发现线上报错日志 org.mybatis.spring.MyBatisSystemException: nested exception is org.apache.ibatis.builder.BuilderException: Error evaluating expression Cause: org.apache.ibatis.ognl.NoSuchPropertyException: 参考 https://github.com/mybatis/mybatis-…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

最新SpringBoot+SpringCloud+Nacos微服务框架分享
文章目录 前言一、服务规划二、架构核心1.cloud的pom2.gateway的异常handler3.gateway的filter4、admin的pom5、admin的登录核心 三、code-helper分享总结 前言 最近有个活蛮赶的,根据Excel列的需求预估的工时直接打骨折,不要问我为什么,主要…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

[ACTF2020 新生赛]Include 1(php://filter伪协议)
题目 做法 启动靶机,点进去 点进去 查看URL,有 ?fileflag.php说明存在文件包含,原理是php://filter 协议 当它与包含函数结合时,php://filter流会被当作php文件执行。 用php://filter加编码,能让PHP把文件内容…...

Unity UGUI Button事件流程
场景结构 测试代码 public class TestBtn : MonoBehaviour {void Start(){var btn GetComponent<Button>();btn.onClick.AddListener(OnClick);}private void OnClick(){Debug.Log("666");}}当添加事件时 // 实例化一个ButtonClickedEvent的事件 [Formerl…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

CVPR2025重磅突破:AnomalyAny框架实现单样本生成逼真异常数据,破解视觉检测瓶颈!
本文介绍了一种名为AnomalyAny的创新框架,该方法利用Stable Diffusion的强大生成能力,仅需单个正常样本和文本描述,即可生成逼真且多样化的异常样本,有效解决了视觉异常检测中异常样本稀缺的难题,为工业质检、医疗影像…...
