Mysql--技术文档--B+树-数据结构的认知
阿丹解读:
之前的文章中写道了有关mysql底层索引,那么在数据量特别大的情况下。mysql采用了B+来管理索引。和存储的数据。
Mysql--技术文档--索引-《索引为什么查找数据快?》-超底层详细说明索引_一单成的博客-CSDN博客
B树解读:
Mysql--技术文档--B树-数据结构的认知_一单成的博客-CSDN博客
基本概念-B+树/B树
B树(B-tree)和B+树(B+ tree)是常见的自平衡搜索树数据结构,用于在存储和检索大量数据时提供高效的操作。它们具有一些共同的基本概念:
节点(Node):B树和B+树的数据存储在节点中。节点可以包含多个关键字和对应的指针。在B树中,叶子节点和内部节点的结构相同,都存储数据和关键字。而在B+树中,叶子节点只存储关键字和指向数据的指针,而内部节点存储关键字和指向子节点的指针。
关键字(Key):关键字是B树和B+树中用于对数据进行排序和搜索的值。关键字按照升序排列,并被存储在节点中。
指针(Pointer):指针用于连接节点,形成树的结构。在B树和B+树中,指针可以指向子节点、父节点或兄弟节点,实现树的平衡。
根节点(Root Node):根节点是B树和B+树的顶层节点。它是树的起点,通过根节点可以访问到整个树的结构。
叶节点(Leaf Node):叶节点是树的最底层节点。在B树中,叶节点存储数据和关键字。而在B+树中,叶节点只存储关键字和指向数据的指针。叶节点之间通过指针进行连接,形成一个有序的双向链表。
内部节点(Internal Node):内部节点是B树和B+树中非叶节点。它们用于指向子节点,并存储关键字。
B树和B+树作为自平衡的搜索树,具有增删改查的操作,每次操作后都会进行平衡以保持树的高度接近最小值。这样可以确保查询效率的稳定性,并提供高效的范围查询和区间搜索能力。
以上是B树和B+树的基本概念,它们在实际应用中有着广泛的应用,尤其在数据库和文件系统中用于管理和查找大量数据。
B+树
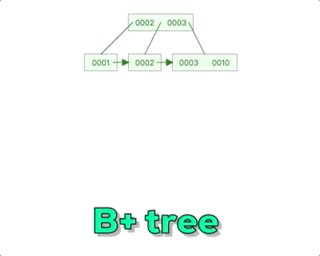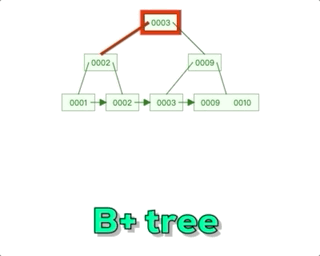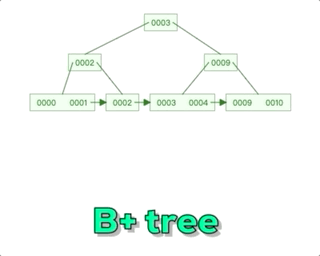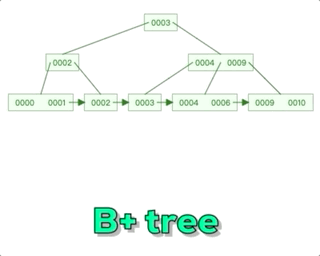
B+树相对于B树主要有一个关键区别,那就是在每个子节点之间添加了指针。在B+树中,所有的数据记录都存储在叶子节点上,而非叶子节点只存储索引信息。每个非叶子节点都有指向其子节点的指针,形成一个链表结构,这个链表结构使得在范围查询时更加高效。而对于B树,非叶子节点既存储索引信息又存储部分数据记录。所以可以说B+树的设计更适合在数据库等需要范围查询的场景中使用。这种设计有效地减少了磁盘I/O操作的次数,提高了查询效率。
当谈到B+树和B树的区别时,以下是一些重要的方面需要考虑:
-
数据记录存储:在B树中,每个节点都包含索引和对应的数据记录。而在B+树中,只有叶子节点包含数据记录,而非叶子节点只包含索引信息。这使得B+树的叶子节点形成了一个有序链表,便于范围查询操作。
-
非叶子节点的指针:在B树中,非叶节点包含指向子节点的指针。而在B+树中,非叶子节点只包含指向子节点的指针,并且这些指针形成了一个链表结构。这样的设计可以更快地在范围查询时遍历数据。
-
查询性能:由于B+树的叶子节点上存储了较多的数据记录,并且有序排列,所以范围查询效率更高。而B树需要在非叶子节点和叶子节点之间来回检索,相对而言,范围查询的性能较差。
-
插入和删除操作:对于B+树来说,由于只需调整叶子节点的指针,所以插入和删除操作相对较快。而B树在插入和删除时可能需要在非叶子节点之间进行调整。
总体来说,B+树在数据库系统中更为常见,尤其在需要范围查询和排序的场景中非常适用。对于大型数据库,B+树的使用可以提供更高的性能和效率。而B树在一些特殊场景中可能仍然有其应用,但在绝大多数情况下,B+树是更好的选择。
B+树复杂度
B+树的复杂度取决于具体的操作,下面是一些常见操作的复杂度分析:
-
插入和删除:B+树的插入和删除操作通常具有O(log N)的时间复杂度,其中N是树中的节点数。插入和删除通常需要在树的高度上进行搜索,并且在找到合适的位置后,可能需要进行节点的分裂或合并操作。
-
查找:B+树的查找操作也具有O(log N)的时间复杂度。通过从根节点开始,根据索引值逐级搜索子节点,直到叶子节点找到目标记录。
-
范围查询:由于B+树的叶子节点形成有序链表,使得范围查询操作非常高效。通过定位范围的起始和结束位置,可以在O(log N + M)的时间复杂度内定位到范围内的M个记录。
注意:这些复杂度分析是对平衡的B+树而言。在实际使用中,性能可能受到硬件、存储引擎、数据分布和索引设计等多个因素的影响。因此,在特定情况下,可能需要进一步考虑这些因素以获得更准确的性能评估。
提供一个网址可手动看见树的工作流程
B-Tree Visualization
详解工作流程
-
B+树的根节点是一个特殊的节点,存储在内存中,并且是树的入口点。根节点可以包含一些索引信息,指向下层节点。
-
当需要插入一条记录时,首先从根节点开始,按照索引值逐级向下搜索,找到合适的叶子节点。在叶子节点中,根据索引值的顺序将记录插入到合适的位置。
-
如果插入操作导致叶子节点超过了预设的容量,会进行节点的分裂操作。分裂会创建一个新的叶子节点,并将一部分记录移动到新节点中。同时,更新上层节点的索引信息以反映叶子节点的变化。
-
当需要删除一条记录时,同样从根节点开始搜索,找到包含目标记录的叶子节点,并将其删除。
-
如果删除操作导致叶子节点的记录数过少,会进行节点的合并操作。合并操作会将相邻的叶子节点合并为一个节点,并更新上层节点的索引信息。
-
在B+树中进行范围查询时,首先定位到起始位置和结束位置所在的叶子节点,然后按照链表结构遍历那些在范围内的叶子节点,找到满足条件的记录。
总之,B+树的工作流程是从根节点开始,按索引值逐级搜索,最终找到叶子节点来插入、删除或查询记录。在修改树的结构时,可能需要进行节点的分裂和合并操作,以保持树的平衡性。这种工作流程使得B+树在数据库中成为一种高效的索引结构,适用于大规模数据存储和高性能查询的场景。
相对于B树的升级点以及特性点
-
范围查询效率更高:B+树的叶子节点形成有序链表,使得范围查询操作更高效。通过链表结构,可以轻松地在范围内遍历叶子节点,从而实现更快速的范围查询。
-
只有叶子节点存储数据记录:在B+树中,只有叶子节点存储数据记录,而非叶子节点只存储索引信息。这种设计减少了冗余数据的存储,提高了数据存储的效率。
-
非叶子节点的指针:B+树的非叶子节点包含指向子节点的指针,并形成链表结构。这样的设计使得范围查询更高效,因为只需要在链表上遍历节点,而不需要返回到父节点进行下一步搜索。
-
插入和删除操作更高效:插入和删除操作只需要在叶子节点上进行操作,而不需要涉及到上层非叶子节点。这样可以减少操作的复杂性和开销,提高了插入和删除操作的效率。
-
有利于磁盘I/O的优化:B+树的有序链表结构有利于优化磁盘I/O操作。通过顺序读取叶子节点的数据记录,可以减少随机I/O的次数,提高磁盘访问的效率。
-
适用于大型数据库系统:由于B+树的优化特性,它更适用于大型数据库系统。B+树在处理大量数据和频繁查询时表现良好,具有更好的查询性能和数据存储效率。
总体而言,B+树相对于B树提供了更高效的范围查询、更高的插入和删除效率以及更好的存储效率。这使得B+树成为了许多数据库系统中常用的索引结构。
mysql中的B+树
在MySQL中,B+树被广泛应用于索引结构。B+树在数据库系统中解决了多个问题,并且成为了一种优秀的索引方案,这也是为什么它被使用的原因之一。
以下是MySQL中B+树的应用和解决的问题:
-
高效数据访问:B+树的有序链表结构和索引在叶子节点的使用,使得在数据库中高效地访问和查询数据成为可能。通过树的平衡和有序性,B+树的查询操作可以在最坏情况下以O(log N)的时间复杂度完成,这意味着即使对于大量数据,查询也可以很快完成。
-
范围查询优化:B+树的特性之一是叶子节点形成有序链表,这使得范围查询的执行非常高效。例如,对于给定的范围条件,可以直接定位到范围内的第一个叶子节点,并沿着链表顺序遍历到最后一个满足条件的叶子节点,从而减少了搜索的次数。
-
数据排序:B+树可以根据索引的有序性来对数据进行排序。当表使用B+树作为主键索引时,在插入新记录或更新现有记录时,B+树会自动维护有序性。
-
减少磁盘访问:B+树的有序链表结构和索引的使用有助于优化磁盘I/O操作。通过顺序读取叶子节点,可以减少磁盘随机I/O的次数,从而提高了查询性能。
-
支持快速插入和删除:B+树的插入和删除操作通常只需要操作叶子节点,不涉及上层非叶子节点。这减少了操作的复杂性和开销,提高了插入和删除操作的效率。
总的来说,MySQL中的B+树应用广泛,它解决了高效数据访问、范围查询优化、数据排序和减少磁盘访问等问题。使用B+树作为索引结构可以提供更好的查询性能、支持大型数据库系统,并且具备高效的数据插入和删除操作。
相关文章:

Mysql--技术文档--B+树-数据结构的认知
阿丹解读: 之前的文章中写道了有关mysql底层索引,那么在数据量特别大的情况下。mysql采用了B来管理索引。和存储的数据。 Mysql--技术文档--索引-《索引为什么查找数据快?》-超底层详细说明索引_一单成的博客-CSDN博客 B树解读:…...
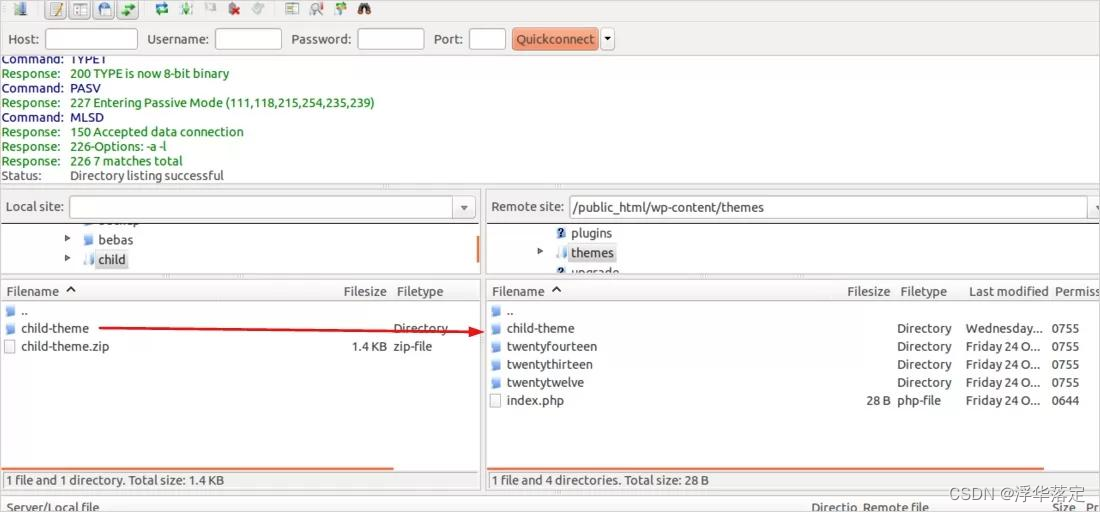
cms之wordpress主题安装
WordPress主题安装教程的方法有两种,分为在线安装和上传安装,下面是主题详细安装方法的步骤。 后台在线安装主题 从后台的主题界面在线安装主题是最方便的WordPress主题安装方式。方法如下: 1 在WordPress后台,转到外观→主题 …...
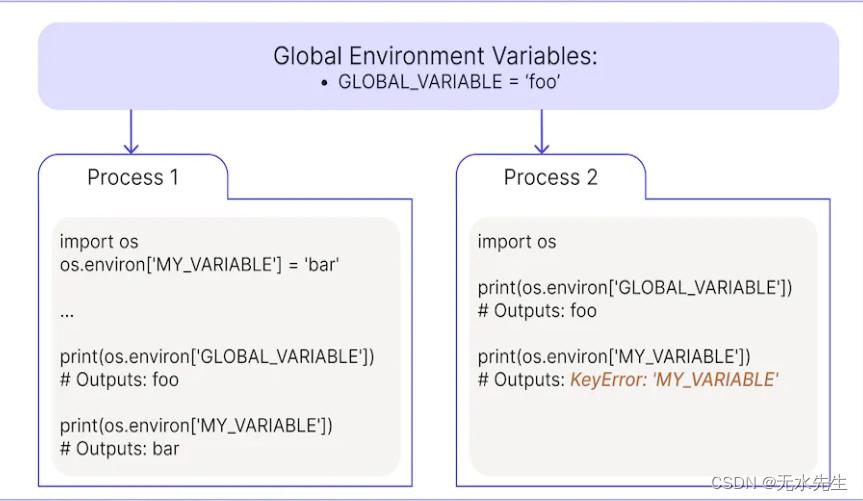
【Python程序设计】Python 中的环境变量【05/8】
一、说明 以下文章是有关 Python 数据工程系列文章的一部分,旨在帮助数据工程师、数据科学家、数据分析师、机器学习工程师或其他刚接触 Python 的人掌握基础知识。本篇将讲述环境变量的问题。 迄今为止,本初学者指南包括: 第 1 部分…...
查漏补缺 - ES6
目录 1,let 和 const1,会产生块级作用域。2,如何理解 const 定义的变量不可被修改? 2,数组3,对象1,Object.is()2,属性描述符3,常用API4,得到除某个属性之外的新对象。 4…...
:最初的项目思路(SLAM))
基于视觉重定位的室内AR导航APP的大创项目思路(1):最初的项目思路(SLAM)
文章目录 最初的项目思路(SLAM):后文: 前情提要: 是第一次做项目的小白,文章内的资料介绍如有错误,请多包含! 最初的项目思路(SLAM): 由于我们在…...
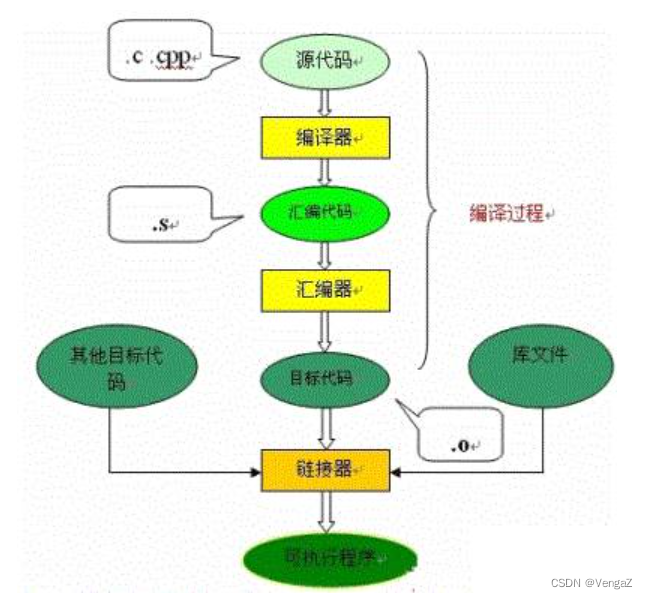
C 编译原理
C 编译原理 目录 C 编译原理引入GCC 工具链介绍C运行库 编译准备工作编译过程1.预处理2.编译3.汇编4.链接 分析ELF文件1.ELF文件的段2.反汇编ELF C语言编译过程 - 摘录编译预处理编译、优化汇编链接过程 引入 大家肯定都知道计算机程序设计语言通常分为机器语言、汇编语言和高…...

服务管理工具systemctl
服务管理工具systemctl Linux服务管理两种方式 service 和 systemctl systemd 是Linux系统最新的初始化系统(init),作用是提高系统的启动速度,尽可能启动较少的进程,尽可能更多进程并发启动. systemd 对应的进程管理命令是systemctlsystemctl 是systemd的主命令,用于管理系统…...
Spring boot环境搭建
使用IDE工具:IntelliJ IDEA 目录 一、安装JAVA 二、安装maven(Java项目管理工具) 三、安装IDE 四、在IDE中配置spring boot项目环境 1、配置jdk 2、配置maven 3、安装创建spring boot项目插件:Spring Assistant 4、安装简…...

【C++】list的模拟实现【完整理解版】
目录 一、list的概念引入 1、vector与list的对比 2、关于struct和class的使用 3、list的迭代器失效问题 二、list的模拟实现 1、list三个基本函数类 2、list的结点类的实现 3、list的迭代器类的实现 3.1 基本框架 3.2构造函数 3.3 operator* 3.4 operator-> 3…...
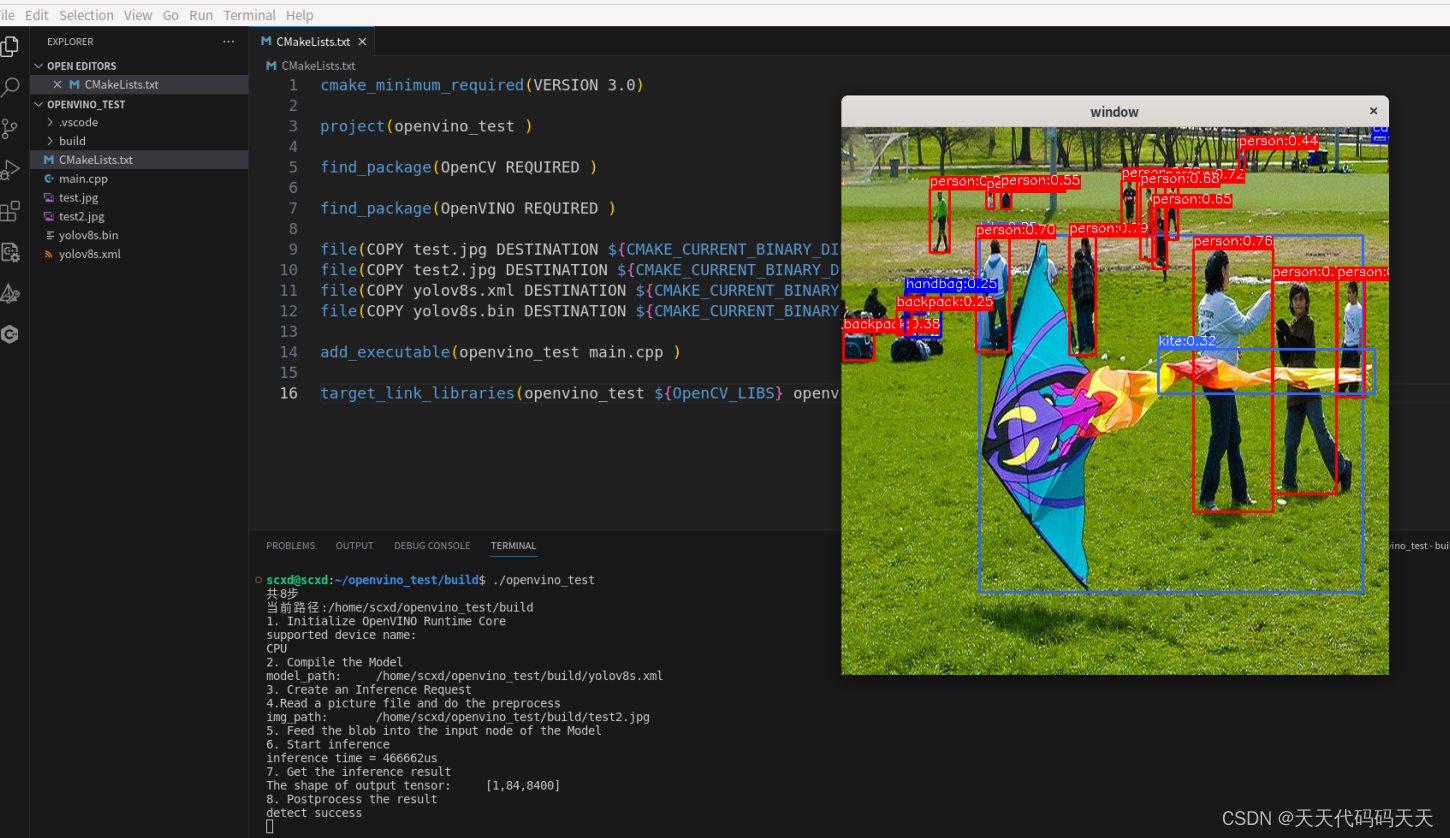
Linux C++ OpenVINO 物体检测 Demo
目录 main.cpp #include <iostream> #include <string> #include <vector> #include <openvino/openvino.hpp> #include <opencv2/opencv.hpp> #include <dirent.h> #include <stdio.h> #include <time.h> #include …...

解决运行Docker镜像报错:version `GLIBC_2.32‘ not found
解决运行Docker镜像,报错:version GLIBC_2.32’ not found 详细报错日志 xapi-backend % docker logs 036de55b5bc6 ./xapi-backend: /lib/aarch64-linux-gnu/libc.so.6: version GLIBC_2.32 not found (required by ./xapi-backend) ./xapi-backend: …...

网络层--IP协议
引入: IP协议主要解决什么问题呢? IP协议提供一种将数据从主机A 发送到 主机B的能力。(有能力不一定能做到,比如小明很聪明,可以考100分,但是他也不是每次搜能考100分࿰…...
Vue2 | Vant uploader实现上传文件和图片
需求: 实现图片和文件的上传,单个图片超过1M则压缩,全部文件加起来不得超过10M。 效果: 1. html <van-form ref"form"><van-field name"uploader" label"佐证材料" required><t…...

第二十一章 Classes
文章目录 第二十一章 ClassesClasses类名和包类定义的基本内容 第二十一章 Classes Classes 类定义并不是 ObjectScript 的正式组成部分。相反,可以在类定义的特定部分中使用 ObjectScript(特别是在方法定义中,可以在其中使用其他实现语言&…...

Ubuntu不能上网解决办法
问题及现象 Ubuntu的虚拟机(18.04)总是莫名就不能上网了。 使用ifconfig -a 查看,ensxx(xx为虚拟机分配的id号)对应的网卡有mac地址,但是没有分配ip地址。 Network中也没有Wired的选项。 临时解决方案 使…...
百度飞浆OCR识别表格入门python实践
1. 百度飞桨(PaddlePaddle) 百度飞桨(PaddlePaddle)是百度推出的一款深度学习平台,旨在为开发者提供强大的深度学习框架和工具。飞桨提供了包括OCR(光学字符识别)在内的多种功能,可…...

直接插入排序、希尔排序详解。及性能比较
直接插入排序、希尔排序详解。及性能比较 一、 直接插入排序1.1 插入排序原理1.2 代码实现1.3 直接插入排序特点总结 二、希尔排序 ( 缩小增量排序 )2.1 希尔排序原理2.2 代码实现2.3 希尔排序特点总结 三、直接插入排序和希尔排序性能大比拼 !!!3.1 如何对比性能?准…...

2023备战秋招Java面试八股文合集
Java就业大环境仍然根基稳定,市场上有很多机会,技术好的人前景就好,就看你有多大本事了。小编得到了一份很不错的资源,建议大家可以认真地来看看以下的资料,来提升一下自己的核心竞争力,在面试中轻松应对面…...

SLAM中的二进制词袋生成过程和工作原理
长期视觉SLAM (Simultaneous Localization and Mapping)最重要的要求之一是鲁棒的位置识别。经过一段探索期后,当长时间未观测到的区域重新观测时,标准匹配算法失效。 当它们被健壮地检测到时,回环检测提供正确的数据关联以获得一致的地图。…...

算法训练第五十九天
503. 下一个更大元素 II - 力扣(LeetCode) 代码: class Solution { public:vector<int> nextGreaterElements(vector<int>& nums) {vector<int> nums1(nums.begin(), nums.end());nums.insert(nums.end(), nums1.beg…...

【Axure高保真原型】引导弹窗
今天和大家中分享引导弹窗的原型模板,载入页面后,会显示引导弹窗,适用于引导用户使用页面,点击完成后,会显示下一个引导弹窗,直至最后一个引导弹窗完成后进入首页。具体效果可以点击下方视频观看或打开下方…...

【OSG学习笔记】Day 18: 碰撞检测与物理交互
物理引擎(Physics Engine) 物理引擎 是一种通过计算机模拟物理规律(如力学、碰撞、重力、流体动力学等)的软件工具或库。 它的核心目标是在虚拟环境中逼真地模拟物体的运动和交互,广泛应用于 游戏开发、动画制作、虚…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

React Native在HarmonyOS 5.0阅读类应用开发中的实践
一、技术选型背景 随着HarmonyOS 5.0对Web兼容层的增强,React Native作为跨平台框架可通过重新编译ArkTS组件实现85%以上的代码复用率。阅读类应用具有UI复杂度低、数据流清晰的特点。 二、核心实现方案 1. 环境配置 (1)使用React Native…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...

省略号和可变参数模板
本文主要介绍如何展开可变参数的参数包 1.C语言的va_list展开可变参数 #include <iostream> #include <cstdarg>void printNumbers(int count, ...) {// 声明va_list类型的变量va_list args;// 使用va_start将可变参数写入变量argsva_start(args, count);for (in…...

关于easyexcel动态下拉选问题处理
前些日子突然碰到一个问题,说是客户的导入文件模版想支持部分导入内容的下拉选,于是我就找了easyexcel官网寻找解决方案,并没有找到合适的方案,没办法只能自己动手并分享出来,针对Java生成Excel下拉菜单时因选项过多导…...

小木的算法日记-多叉树的递归/层序遍历
🌲 从二叉树到森林:一文彻底搞懂多叉树遍历的艺术 🚀 引言 你好,未来的算法大神! 在数据结构的世界里,“树”无疑是最核心、最迷人的概念之一。我们中的大多数人都是从 二叉树 开始入门的,它…...

DAY 26 函数专题1
函数定义与参数知识点回顾:1. 函数的定义2. 变量作用域:局部变量和全局变量3. 函数的参数类型:位置参数、默认参数、不定参数4. 传递参数的手段:关键词参数5 题目1:计算圆的面积 任务: 编写一…...

内窥镜检查中基于提示的息肉分割|文献速递-深度学习医疗AI最新文献
Title 题目 Prompt-based polyp segmentation during endoscopy 内窥镜检查中基于提示的息肉分割 01 文献速递介绍 以下是对这段英文内容的中文翻译: ### 胃肠道癌症的发病率呈上升趋势,且有年轻化倾向(Bray等人,2018&#x…...
