汉诺塔问题(包含了三台柱和四台柱)——C语言版本
目录
1. 什么是汉诺塔
2. 三座台柱的汉诺塔
2.1 思路
2.2 三座台柱的汉诺塔代码
3. 四座台柱的汉诺塔
3.1 思路
3.2 四座台柱的汉诺塔代码
1. 什么是汉诺塔
汉诺塔代码的功能:计算盘子的移动次数,由数学公式知,汉诺塔的盘子移动次数与盘子数n存在这样的关系,移动数 =(由递推得到),后面可以用这个公式来验证我们代码。
汉诺塔的规制:(1)有三根相邻的柱子,标号为A,B,C。(2)A柱子上从下到上按金字塔状叠放着n个不同大小的圆盘。(3)现在把所有盘子一个一个移动到柱子B上,并且每次移动同一根柱子上都不能出现大盘子在小盘子上方。

2. 三座台柱的汉诺塔
2.1 思路

总结:我们想知道n个盘子的次数,记住了,在求解f(n)的时候,我们直接默认f(n - 1)已经完了就可以了!这个在前面已经解释过了,在此不再鳌述。我们将n-1个盘子当作一个整体:这就是类似于分治求解子问题的思想
那么当由3个盘子时,就有公式:f(3,x,y,z) = f(2,x,z,y),x->z,f(2,y,x,z);当有4个盘子时,就有公式:f(4,x,y,z) = f(3,x,z,y),x->z,f(3,y,x,z).从而推出f(n,x,y,z) = f(n,x,z,y),x->z,f(n,y,x,z)!
综上所述:也就是说我们想移动n个盘子,就需要先移动n - 1个盘子;移动n - 1个盘子,就需要先移动n - 2个盘子 ………………;移动2个盘子,就必须先移动1个盘子;
(1)而移动1个盘子就是递归的终止条件
(2)而n个盘子变成n - 1个盘子就是递归的大问题变成小问题的方法
2.2 三座台柱的汉诺塔代码
下列代码展示了盘子在柱子上移动的顺序:

下列代码展示了有n个盘子,至少移动几次:

对 (展示了有n个盘子,至少移动几次)解析:
ps:小伙伴们,图片将就着看吧哈哈哈,gif制作软件的免费用户是这样的w(゚Д゚)w!

通过3个盘子,我们可以分析得:
(1)想先移动第3个盘子到最终位置,就必须先移动上面2个盘子;
(2)上面2个盘子总共移动了两趟,这就是2 * moveCount3(n - 1)的原因;
(3)最底下的盘子是移动了一次,这就是2 * moveCount3(n - 1) + 1的原因;
总结:
有n个盘子,上面n - 1个盘子需要移动两趟,而最底下,也就是第n个盘子是移动1次!!!
3. 四座台柱的汉诺塔
3.1 思路
算法思想:
用如下算法移动盘子(记为fourHanoi):
将A柱上n个盘子划分为上下两部分,上方部分共有m(1≤m≤n)个盘子,下方部分共有n - m个盘子。
步骤一:将A柱上面部分m个盘子使用fourHanoi算法经过C、D柱移至B柱。(此时C、D是中间柱)
步骤二:将A柱剩余的n - m个盘子使用threeHanoi算法经过C柱移至D柱。(此时C柱是中间柱)
步骤三:将B柱上的m个盘子使用fourHanoi算法经过A、C柱移至D柱。(此时A、C柱是中间柱)
这就有伙伴有疑问了,为什么不能全部都使用fourHanoi算法?
答:因为当fourHanoi算法将盘子转移到一定程度后,有个柱子上的盘子就不能动了,可以当作少了座台柱,也就是只能用threeHanoi算法移动其它盘子了。所以我们在计算的时候,就是在找fourHanoi算法将盘子转移到一定程度的临界值,也就是找多少个盘子能使用fourHanoi算法(找m)
根据算法的思想,可知:
(1)最优子结构性质:
四柱汉诺塔问题的最优解是用最少的移动次数将A柱上的盘子全部移到D柱上。当盘子总数为i时,我们不妨设使用fourHanoi的最少移动次数为f(i)。相应的threeHanoi 算法移动次数为g(n - m),由于g(n - m)=2g(n - m - 1)+1=2^(n - m) -1,当n - m确定时,g(n - m)也是不变的。
f(m)为最优解时,其子问题f(m - 1)也必为最优解。如果f(m - 1)不是最优解,那么存在f’(m - 1) < f(m - 1)。用f’(m - 1)替换f(m - 1)将产生一个比f(m)更优的解。这与f(m)为最优解是矛盾的。所以本问题具有最优子结构性质。
(2)递归地定义问题的最优解:
根据上述fourHanoi算法得到最少移动次数f(m):
①当n = 1时,有
②当n > 1时,有
3.2 四座台柱的汉诺塔代码
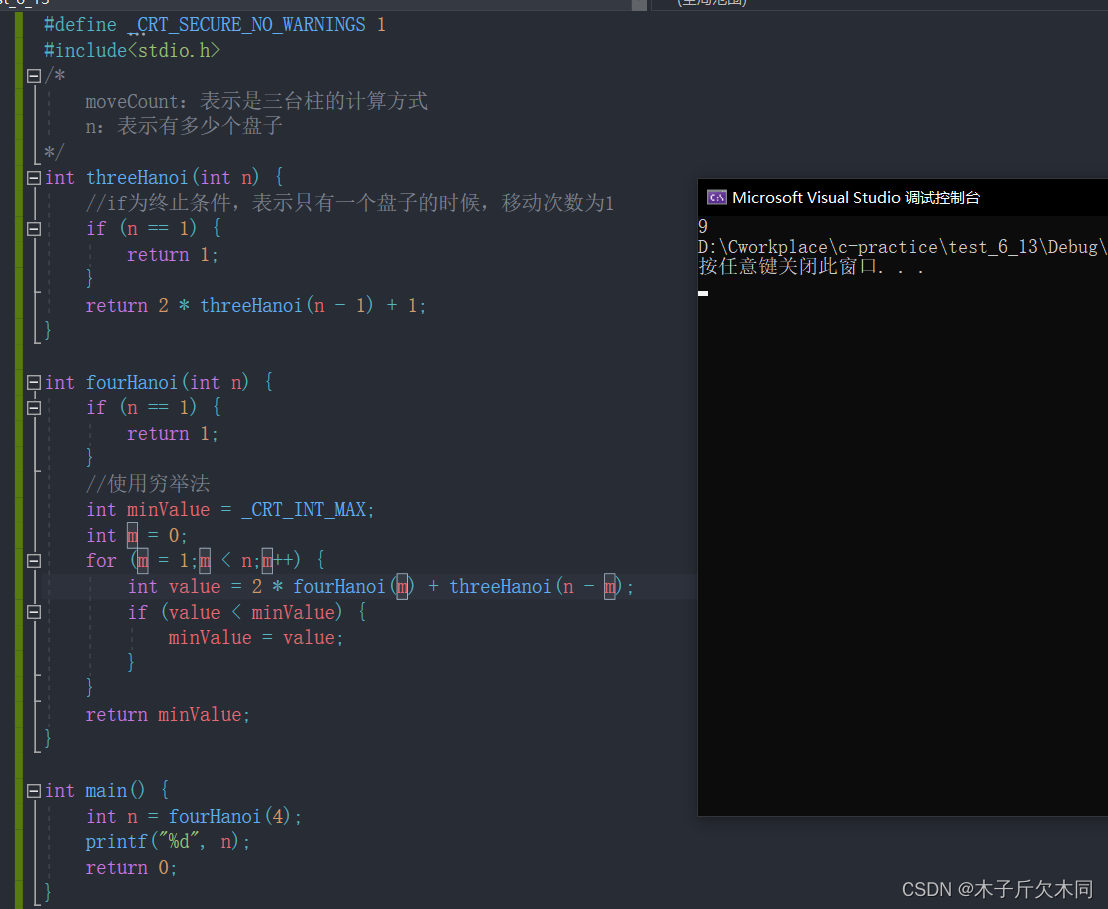
相关文章:

汉诺塔问题(包含了三台柱和四台柱)——C语言版本
目录 1. 什么是汉诺塔 2. 三座台柱的汉诺塔 2.1 思路 2.2 三座台柱的汉诺塔代码 3. 四座台柱的汉诺塔 3.1 思路 3.2 四座台柱的汉诺塔代码 1. 什么是汉诺塔 汉诺塔代码的功能:计算盘子的移动次数,由数学公式知,汉诺塔的盘子移动次数与…...
【实训项目】滴滴电竞APP
1.设计摘要 2013年国家体育总局决定成立一支由17人组成的电子竞技国家队,第四届亚室会中国电竞代表队 出战第四届亚洲室内和武道运动会。 2014年1月13日CCTV5《体育人间》播放英雄联盟皇族战队的纪录片。 在2015到2019年间,我国电竞战队取得的无数值得…...
C++核心编程--类篇
C核心编程 1.内存分区模型 C程序在执行时,将内存大方向分为4个区域 意义:不同区域存放数据,赋予不同的生命周期,更能灵活编程 代码区:存放函数体的二进制代码,由操作系统进行管理的全局区:存放…...

java中用feign远程调用注解FeignClient的时候不重写Encoder和Decoder怎么格式不对呢?
如果在使用 Feign 进行远程调用时,没有重写 Encoder 和 Decoder,但仍然遇到格式不对的问题,可能是由于以下原因之一: 服务端返回的数据格式与客户端期望的格式不匹配:Feign 默认使用基于 Jackson 的 Encoder 和 Decode…...

记录使用Docker Compose 部署《XAPI项目》遇道的问题及解决方案
《XAPI项目》:GitHub仓库(勿打🚫小破站一个) 这篇文档,主要内容是记录使用Docker Compose 部署《XAPI项目》遇道的问题及解决方案 目录 📚 本地MySQL数据如何导入到容器内的MySQL中❎ 解决报错:…...

腾讯云OCR实践 - 降低客服财务运营成本
一、 前言: 随着图片时代的飞速发展,大量的文字内容为了优化排版和表现效果,都采用了图片的形式发布和存储,这为内容的传播和安全性带来了很大的便利,需要做重复性劳动。 OCR文字扫描工具也逐渐的应运而生,…...

springboot+vue上传图片
这里是一个简单的示例,演示了如何在Spring Boot中从Vue.js上传图像: 1.前端Vue.js代码: <template><div><input type"file" change"handleFileUpload"><button click"uploadImage">…...

高压电缆护层接地环流及温度在线监测系统
高压电缆的金属护层是电缆的重要组成部分,当缆芯通过电流时,会在金属护层上产生环流,外护套的绝缘状态差、接地不良、金属护层接地方式不正确等等都会引起护套环流异常现象,严重威胁电缆运行安全。 当电缆金属护层环流出现异常时…...

无涯教程-JavaScript - IPMT函数
描述 IPMT函数根据定期,固定的还款额和固定的利率返回给定投资期限内的利息支付。 语法 IPMT (rate, per, nper, pv, [fv], [type])争论 Argument描述Required/OptionalRateThe interest rate per period.RequiredPerThe period for which you want to find the interest a…...

【EI会议征稿】第三届机械自动化与电子信息工程国际学术会议(MAEIE 2023)
第三届机械自动化与电子信息工程国际学术会议(MAEIE 2023) 第三届机械自动化与电子信息工程国际学术会议(MAEIE 2023)将于2023年12月15-17日在江苏南京举行。本会议通过与业内众多平台、社会各团体协力,聚集机械自动…...

手写实现LRN局部响应归一化算子
1、重写算子的需求 芯片推理过程中遇到很多算子计算结果不对的情况,原因是封装的算子会在某些特殊情况下计算超限,比如输入shape特别大或者数值特别大时,LRN算子计算会出现NAN值,所以需要重写算子。先对输入数据做一个预处理&…...

朗思科技数字员工通过统信桌面操作系统兼容性互认认证
近日,朗思科技数字员工与统信桌面操作系统V20进行了兼容互认,针对上述产品的功能、兼容性方面,通过共同严格测试表明——朗思科技数字员工在统信桌面操作系统 V20上整体运行稳定,满足功能及兼容性测试要求。 北京朗思智能科技有限…...
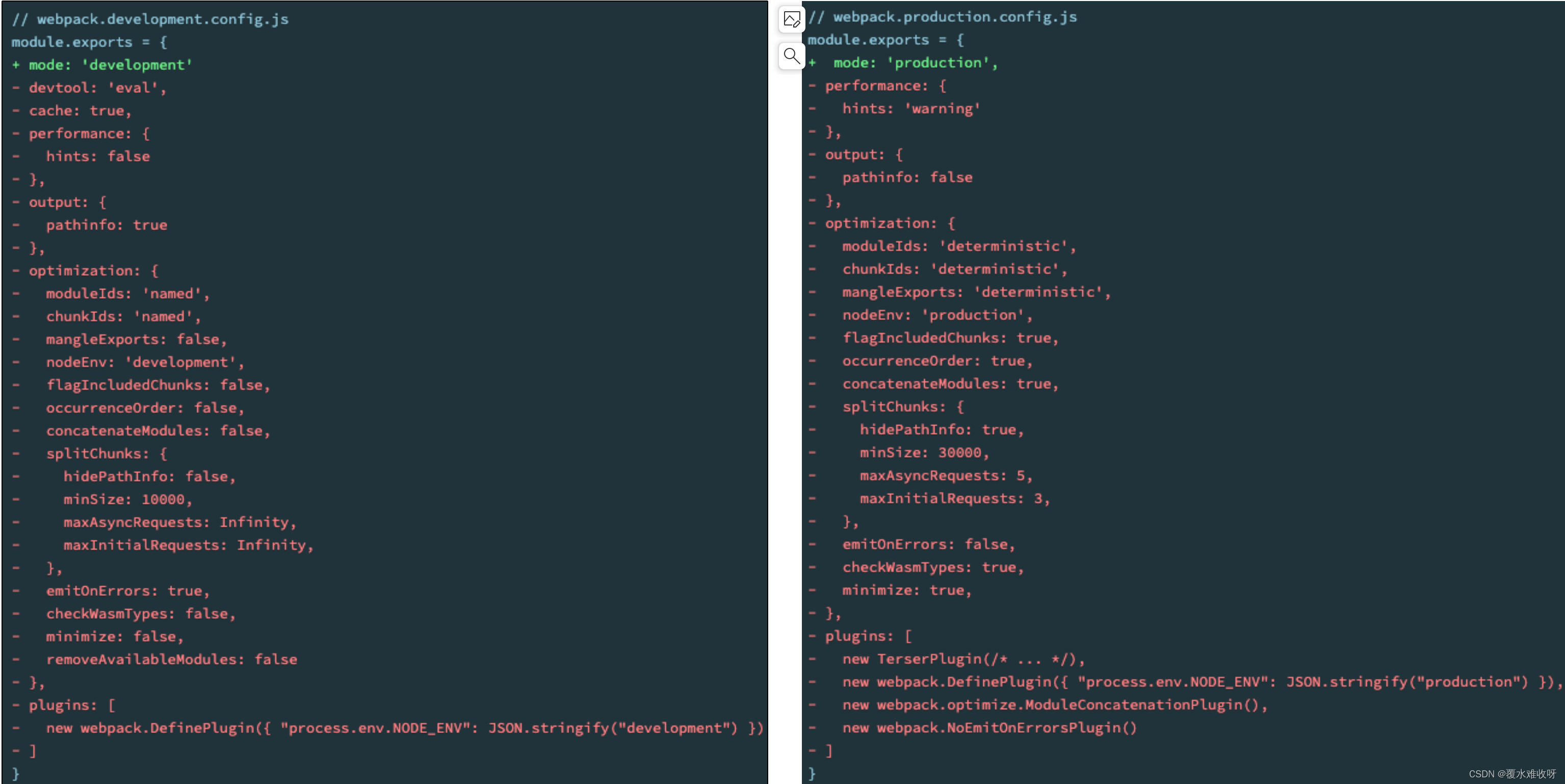
十六、Webpack常见的插件和模式
一、认识插件Plugin Webpack的另一个核心是Plugin,官方有这样一段对Plugin的描述: While loaders are used to transform certain types of modules, plugins can be leveraged to perform a wider range of tasks like bundle optimization, asset m…...

ChatGPT新增超强插件:文本直接生成视频、海报,支持自定义修改!
全球著名在线设计平台Canva,在ChatGPT Plus(GPT-4)上推出了插件功能,用户通过文本提示,几秒钟就能生成演示文稿、PPT插图、电子书封面、宴会邀请函等各种精美设计海报,同时支持生成视频。 该插件最强大的功…...

亚像素边缘提取的例子
求帮忙下载: 1.http://download.csdn.net/detail/pkma75/925394 pkma75 资源积分:1分 备注:pdf格式,用曲线拟合的方法计算亚像素,编程易实现,具有较强的实用价值 2.http://download.csdn.net/detail/kua…...

Wayland:推动Linux桌面进入下一代图形显示时代
文章首发地址 Wayland是Linux系统下的一种图形显示协议,旨在替代X Window System(X11)作为Linux桌面环境的图形显示服务。下面是对Wayland的详细解释: 背景: 传统的Linux桌面环境使用X Window System(X11&…...
)
mysql外键(foreign key)
简介 MySQL的外键约束用来在两个表数据之间建立链接,其中一张表的一个字段被另一张表中对应的字段约束。也就是说,设置外键约束至少要有两种表,被约束的表叫做从表(子表),另一张叫做主表(父表&…...
内网穿透——Windows搭建服务器
文章目录 1.前言2. Emby网站搭建2.1. Emby下载和安装2.2 Emby网页测试 3. 本地网页发布3.1 注册并安装cpolar内网穿透3.2 Cpolar云端设置3.3 Cpolar内网穿透本地设置 4.公网访问测试5.结语 1.前言 在现代五花八门的网络应用场景中,观看视频绝对是主力应用场景之一&…...

UE5.1 + Android 环境搭建
官方文档:一定一定一定要参照官方文档,因UE不同版本对应的环境搭建并不完全一致。 准备工作 通过EpicGameLaunch下载Android目标平台。 必须安装jdk1.8并配置环境变量,UE5.1不要使用最新的jdk20;下载地址 安装 Android Studio …...

华为python面试题目
华为Python常见的面试问题包括: Python是如何被解释的?什么是PEP8?Python是怎样管理内存的?什么是Python装饰器?Python提供哪些内置类型?Python中的异常处理是怎样的?什么是Python的上下文管理器?Python中的列表推导式是什么?Python中的生成器是什么?什么是Python的装…...

网络编程(Modbus进阶)
思维导图 Modbus RTU(先学一点理论) 概念 Modbus RTU 是工业自动化领域 最广泛应用的串行通信协议,由 Modicon 公司(现施耐德电气)于 1979 年推出。它以 高效率、强健性、易实现的特点成为工业控制系统的通信标准。 包…...

零门槛NAS搭建:WinNAS如何让普通电脑秒变私有云?
一、核心优势:专为Windows用户设计的极简NAS WinNAS由深圳耘想存储科技开发,是一款收费低廉但功能全面的Windows NAS工具,主打“无学习成本部署” 。与其他NAS软件相比,其优势在于: 无需硬件改造:将任意W…...

深入剖析AI大模型:大模型时代的 Prompt 工程全解析
今天聊的内容,我认为是AI开发里面非常重要的内容。它在AI开发里无处不在,当你对 AI 助手说 "用李白的风格写一首关于人工智能的诗",或者让翻译模型 "将这段合同翻译成商务日语" 时,输入的这句话就是 Prompt。…...

Linux链表操作全解析
Linux C语言链表深度解析与实战技巧 一、链表基础概念与内核链表优势1.1 为什么使用链表?1.2 Linux 内核链表与用户态链表的区别 二、内核链表结构与宏解析常用宏/函数 三、内核链表的优点四、用户态链表示例五、双向循环链表在内核中的实现优势5.1 插入效率5.2 安全…...

css实现圆环展示百分比,根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...

VB.net复制Ntag213卡写入UID
本示例使用的发卡器:https://item.taobao.com/item.htm?ftt&id615391857885 一、读取旧Ntag卡的UID和数据 Private Sub Button15_Click(sender As Object, e As EventArgs) Handles Button15.Click轻松读卡技术支持:网站:Dim i, j As IntegerDim cardidhex, …...

【git】把本地更改提交远程新分支feature_g
创建并切换新分支 git checkout -b feature_g 添加并提交更改 git add . git commit -m “实现图片上传功能” 推送到远程 git push -u origin feature_g...

令牌桶 滑动窗口->限流 分布式信号量->限并发的原理 lua脚本分析介绍
文章目录 前言限流限制并发的实际理解限流令牌桶代码实现结果分析令牌桶lua的模拟实现原理总结: 滑动窗口代码实现结果分析lua脚本原理解析 限并发分布式信号量代码实现结果分析lua脚本实现原理 双注解去实现限流 并发结果分析: 实际业务去理解体会统一注…...
-HIve数据分析)
大数据学习(132)-HIve数据分析
🍋🍋大数据学习🍋🍋 🔥系列专栏: 👑哲学语录: 用力所能及,改变世界。 💖如果觉得博主的文章还不错的话,请点赞👍收藏⭐️留言Ǵ…...

在鸿蒙HarmonyOS 5中使用DevEco Studio实现企业微信功能
1. 开发环境准备 安装DevEco Studio 3.1: 从华为开发者官网下载最新版DevEco Studio安装HarmonyOS 5.0 SDK 项目配置: // module.json5 {"module": {"requestPermissions": [{"name": "ohos.permis…...
