异步FIFO设计的仿真与综合技术(3)
概述
本文主体翻译自C. E. Cummings and S. Design, “Simulation and Synthesis Techniques for Asynchronous FIFO Design 一文,添加了笔者的个人理解与注释,文中蓝色部分为笔者注或意译。前文链接:
异步FIFO设计的仿真与综合技术(2)![]() https://blog.csdn.net/apple_53311083/article/details/132856486?spm=1001.2014.3001.5502 我们继续书结上回,来学习为什么异步FIFO中格雷码的使用
https://blog.csdn.net/apple_53311083/article/details/132856486?spm=1001.2014.3001.5502 我们继续书结上回,来学习为什么异步FIFO中格雷码的使用
3.0 格雷码计数器(Gray code counter)
格雷码是以Frank Gray的名字命名的,他在1953年最初申请该编码专利,设计一个格雷码计数器有多种方法。本节详细介绍了一种简单而直接的设计方法。本文中描述的技术只使用了一组触发器作为格雷码计数器,第二种使用两组触发器来实现更高速度的方法在第4.0节中展示。
3.1 格雷码模式(Gray code patterns)
我们希望同时创建一个n位格雷码计数器和一个(n-1)位格雷码计数器(原因后面会说)。分别创建两个计数器当然很容易,但是创建一个通用的n位格雷码计数器,然后修改第二个MSB,通过共享LSBs构成一个(n-1)位格雷码计数器也是很容易和高效的。在本文中,这种方法被称为“双n位格雷码计数器”(dual n-bit Gray code counter)。

为了更好地理解将n位格雷码转换为(n-1)位格雷码的问题,我们考虑创建一个双4位和3位格雷码计数器的示例,如图2所示 。
最常见的格雷码,如图2所示,是一个反射(reflected)编码,其中除了MSB位之外,任何列中的位都关于序列中点对称。这意味着4位格雷码的后半部分是MSB倒置的前半部分的镜像。
要把一个4位格雷码转换到3位,我们不希望4位序列的后半部分的LSBs是前半部分的LSBs的镜像,相反,我们希望后半部分的LSBs重复前半部分的4位LSBs。
经过更仔细的检查,很明显,反转4位格雷码的后半部分的第二个MSB(第二高位,这里指的就是从右往左数第二位)将在4位序列的三个LSB中产生所需的3位格雷码序列。唯一的问题是,具有额外MSB的3位格雷码不再是真正的格雷码,因为当序列从7(格雷码0100)改为8(~格雷码1000),再从15(~格雷码1100)改为0(格雷码0000)时,两位变化而不是一位。一个真正的格雷码在相邻数据之间只改变一位(这部分内容结合上面的图二应该解释的比较清楚)。
3.2 格雷码计数基础(Gray code counter basics)
关于格雷码,我们首先要明确的就是:任意两个相邻数之间的代码距离只有1(从一个格雷码变到相邻的另一个格雷码的时候,只有一个位可以改变)。第二点需要明确的是:当计数总量为2的幂次时,格雷码计数最有效。可以制作一个计数偶数个序列的格雷码计数器,但对这些序列的转换通常不像标准的格雷码那么简单。还要注意,没有计数奇数的格雷码计数器,所以人们不能制作一个计数值为23的格雷码代码。基于此,本文所设计的FIFO的深度被设置为。
图3是一个样式为#1的双n位格雷码计数器的框图。样式#1格雷码计数器假设寄存器位的输出是格雷码值本身(ptr、wptr或rptr)。格雷码输出被传递到格雷码-二进制转换器(bin),bin被传递到一个条件二进制值递增器以生成下一个二进制计数值(bnext),bnext被传递到二进制-格雷码转换器,该转换器生成下一个格雷码计数值(gnext),gnext被传递到寄存器输入。图3方框图的上半部分表示了所描述的逻辑流,而下半部分表示了下一节中描述的第二个格雷码计数器相关的逻辑。
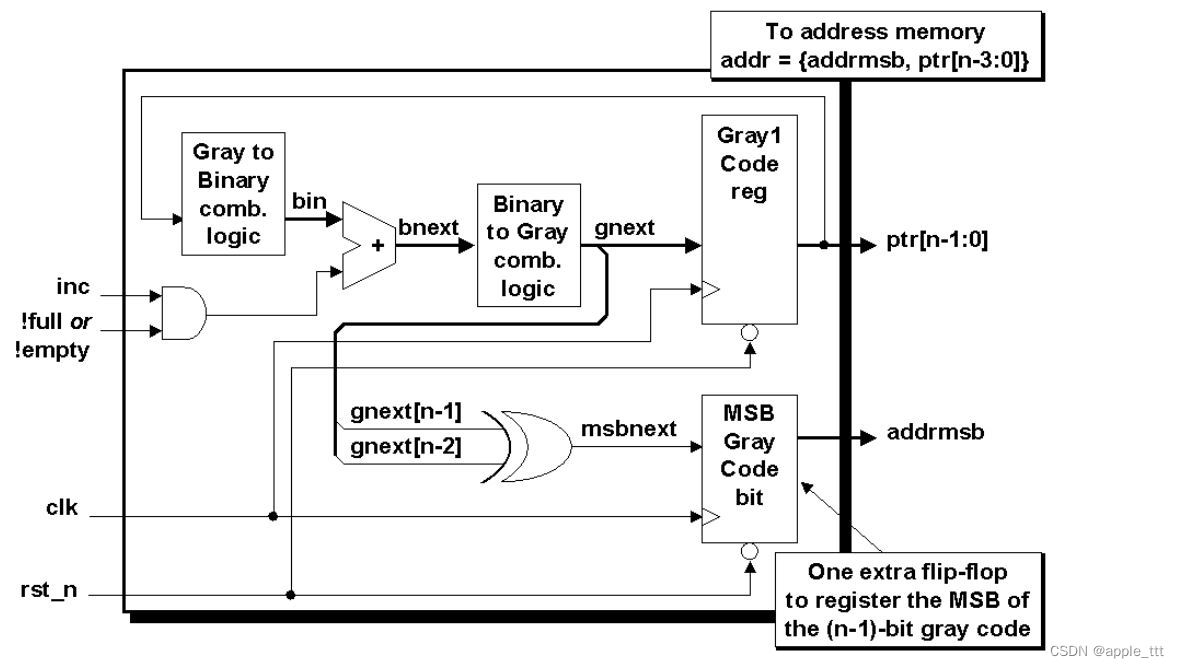
3.3 双n位格雷码计数器(Dual n-bit Gray code counter)
双n位格雷码计数器同时生成n位格雷码序列(见第3.2节所述)和(n-1)位格雷码序列。
(n-1)位格雷码只是通过对n位格雷码的两个MSB进行异或操作来生成,以生成(n-1)位格雷码的MSB。这与n位格雷码计数器的(n-2)个LSBs结合起来,形成(n-1)位格雷码计数器。
这里我们来简单解释一下,从3.1节中,我们知道,n-1位格雷码的生成方式是把格雷码的下半部分(MSB为1的部分)的第二高位(第二个MSB)翻转(0变1,1变0),这里我们的gnext[n-1]其实就是我们的MSB(在这里甚至可以直接理解成就是1),gnext[n-2]就是我们的第二个MSB,也就是gnext[n-2]与数据1进行异或操作,我们知道0和1异或结果是1,1和1异或结果是0,也就完成了第二高位的翻转,然后与剩下的LSBs进行拼接,就得到了n-1位的格雷码。
3.4 关于格雷码计数器的额外注意事项(Additional Gray code counter considerations)
二进制值递增器采用“如果未满”或“如果未空”测试,以确保适当的FIFO指针在FIFO满或FIFO空条件期间不会增加。
如果在生效FIFO满条件时,向FIFO发送数据的逻辑块能可靠地停止发送数据,则可以通过从FIFO写指针中删除FIFO满测试逻辑来简化FIFO设计。
FIFO指针本身并不保护FIFO缓冲区被覆盖(写覆盖,在写过数据的地方继续写,覆盖原有的数据),但是FIFO额外的条件逻辑可以被添加到FIFO内存缓冲区,以确保在FIFO满状态下写使能信号不能被激活。
可以向指针设计中添加一个附加的“sticky”状态位,即ovf(overflow,溢出)或unf(underflow,下溢出),以指示在FIFO满期间发生额外的FIFO写操作或在FIFO空期间发生额外的FIFO读操作,以指示只有通过复位才能清楚的错误情况。
一个安全、通用的FIFO设计将包括上述的保障措施,代价是稍大和可能较慢的实现。这是一个好主意,因为未来的同事可能会尝试在另一个设计中复制和重用代码,而不理解当前设计中所考虑的所有重要细节。
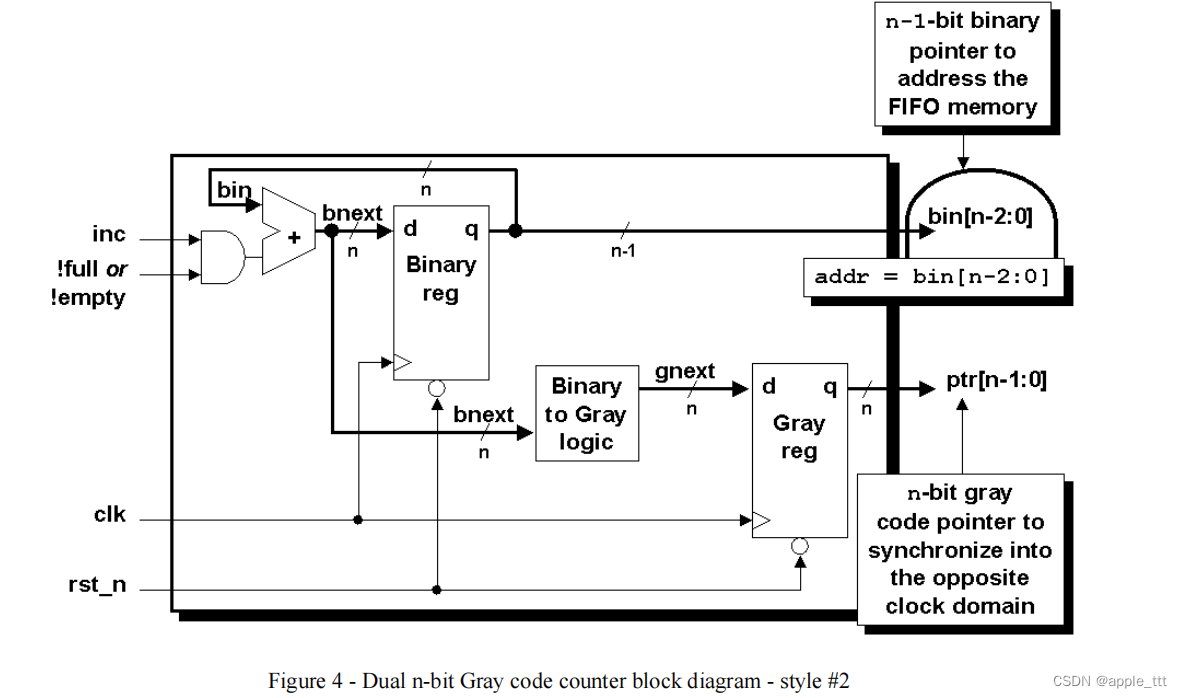
4.0 格雷码计数器-风格2(Gray code counter - Style #2)
从本文的1.2版本开始,FIFO实现使用了格雷码计数器-样式#2,它实际上使用了两组寄存器来消除将格雷码指针值转换为二进制值的需要。第二组寄存器(二进制寄存器)也可以用于直接寻址FIFO存储器,而不需要将存储器地址转换为格雷码。n-位的格雷码指针仍然需要将指针同步到相反的时钟域,但是n-1位的二进制指针可以直接用来处理内存。二进制指针还使运行计算更容易,以生成“几乎满”和“几乎空”的位(在本文中没有显示)。
相关文章:

异步FIFO设计的仿真与综合技术(3)
概述 本文主体翻译自C. E. Cummings and S. Design, “Simulation and Synthesis Techniques for Asynchronous FIFO Design 一文,添加了笔者的个人理解与注释,文中蓝色部分为笔者注或意译。前文链接: 异步FIFO设计的仿真与综合技术…...

什么是区块链,解释区块链的原理和应用场景
1、什么是区块链,解释区块链的原理和应用场景。 区块链是一种分布式数据库,它由一系列按照时间顺序排列的数据块组成,并采用密码学方式保证不可篡改和不可伪造。区块链技术最初起源于比特币,作为比特币的底层技术,用于…...

使用bert进行文本二分类
构建BERT(Bidirectional Encoder Representations from Transformers)的训练网络可以使用PyTorch来实现。下面是一个简单的示例代码: import torch import torch.nn as nn from transformers import BertModel, BertTokenizer# Load BERT to…...

用Windows Installer CleanUp Utility 在windows server上面将软件卸载干净,比如SQLSERVER
这里写自定义目录标题 下载文件:Windows Installer CleanUp Utility。 通过以上工具可以将一个应用程序卸载干净。...

Java手写LinkedList和拓展
Java手写LinkedList和拓展 思维导图 #mermaid-svg-K0RTlFFvnikDRvqp {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-K0RTlFFvnikDRvqp .error-icon{fill:#552222;}#mermaid-svg-K0RTlFFvnikDRvqp .error-text{fill…...
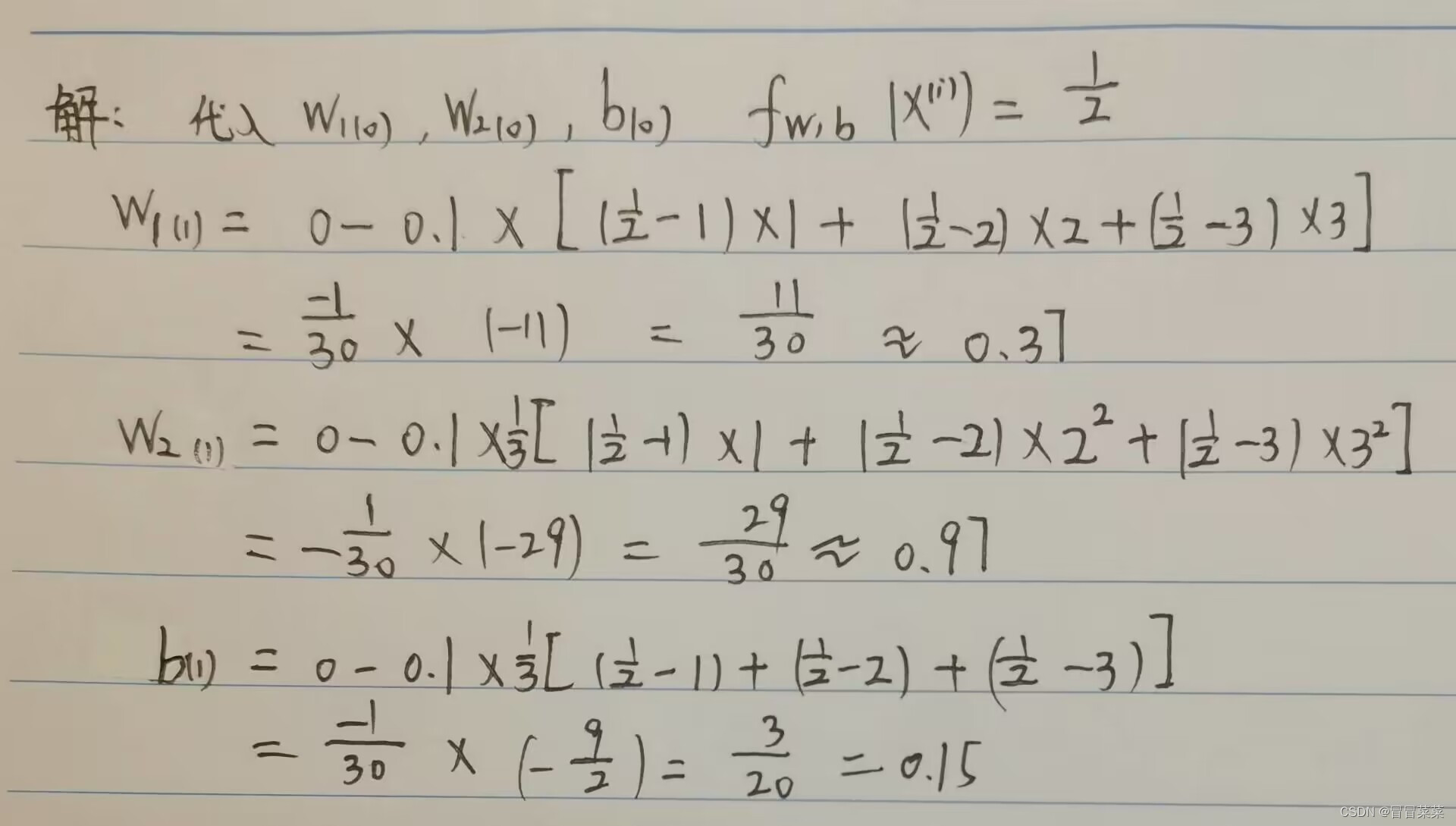
机器学习(14)---逻辑回归(含手写公式、推导过程和手写例题)
逻辑回归 一、逻辑回归概述二、模型、策略和优化(手写)三、w和b的梯度下降公式推导四、例题分析4.1 题目4.2 解答 一、逻辑回归概述 1. 逻辑回归也称作logistic回归分析,是一种广义的线性回归分析模型,属于机器学习中的监督学习。…...
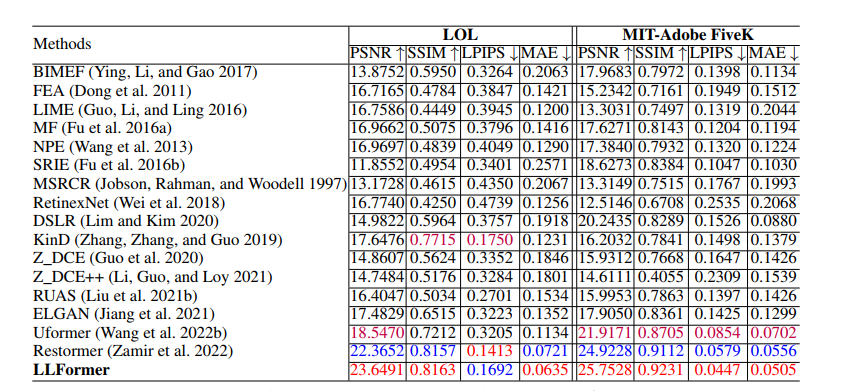
LLFormer 论文阅读笔记
Ultra-High-Definition Low-Light Image Enhancement: A Benchmark and Transformer-Based Method 这是南京大学在AAAI 2023发表的一篇AAAI2023 超高清图像暗图增强的工作。提出了一个超高清暗图增强数据集,提供了4K和8K的图片,同时提出了一个可用于暗图…...

JSP语法基础习题
目录 简答题:jsp中静态include和动态include的区别是什么? 简答题:jsp有哪些内置对象,作用分别是什么? 简答题:Request对象的主要方法有哪些? 代码题: 简答题:jsp中静态…...

vue类与样式的绑定列表渲染
目录 1.类与样式的绑定 1.1绑定 HTML class 1.2绑定数组 1.3绑定内联样式 绑定数组 2.列表渲染 2.1v-for 2.2v-for 与对象 2.3在 v-for 里使用范围值 1.类与样式的绑定 1.1绑定 HTML class 我们可以给 :class (v-bind:class 的缩写) 传递一个对象来动态切换 class…...

vue3+element-plus权限控制实现(el-tree父子级不关联情况处理)
文章目录 前言一、遇到的交互场景el-tree 中 check-strictly 属性 二、处理父级的半选中以及选中交互el-treecheck,check-change 事件编辑进来,父级的半选状态处理 总结 前言 在开发后台管理系统的时候,用户的权限控制是一个常见的需求。这里…...

js中事件委托和事件绑定之间的区别
聚沙成塔每天进步一点点 ⭐ 专栏简介⭐ 事件绑定(Event Binding)⭐事件委托(Event Delegation)⭐ 选择事件绑定或事件委托⭐ 写在最后 ⭐ 专栏简介 前端入门之旅:探索Web开发的奇妙世界 记得点击上方或者右侧链接订阅本…...

Android 11.0 系统system模块开启禁用adb push和adb pull传输文件功能
1.使用场景 在进行11.0的系统定制化开发中,在一些产品中由于一些开发的功能比较重要,防止技术点外泄在出货产品中,禁用 adb pull 和adb push等命令 来获取系统system下的jar 和apk 等文件,所以需要禁用这些命令 2.系统system模块开启禁用adb push和adb pull传输文件功能的…...

实战经验分享:如何通过HTTP代理解决频繁封IP问题
在网络爬虫和数据采集等应用中,频繁遇到目标网站封锁或限制IP的情况是非常常见的。为了解决这个问题,使用HTTP代理是一种有效的方法。本文将与您分享一些实战经验,帮助您通过HTTP代理解决频繁封IP问题,确保您的数据采集工作顺利进…...

通讯网关软件001——利用CommGate X2Access-U实现OPC UA数据转储Access
本文介绍利用CommGate X2ACCESS-U实现从OPC UA Server读取数据并同步转储至ACCESS数据库。CommGate X2ACCESS-U是宁波科安网信开发的网关软件,软件可以登录到网信智汇(http://wangxinzhihui.com)下载。 【案例】如下图所示,实现从OPC UA Server实时读取…...
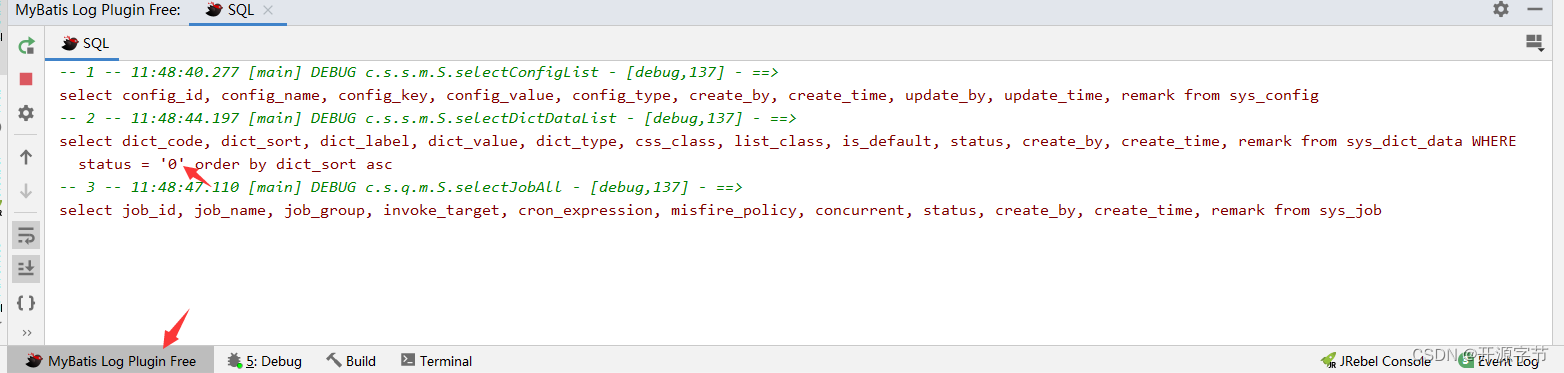
Mybatis sql参数自动填充
问题描述 在日常开发中,经常会遇到Mybatis sql语句的操作问题,由于Mybatis实现sql的动态拼接,开发过程中,为了验证sql是否书写正确,通常需要获取的控制台打印的sql语句来检查是否拼接正确。如下图所示: 那…...
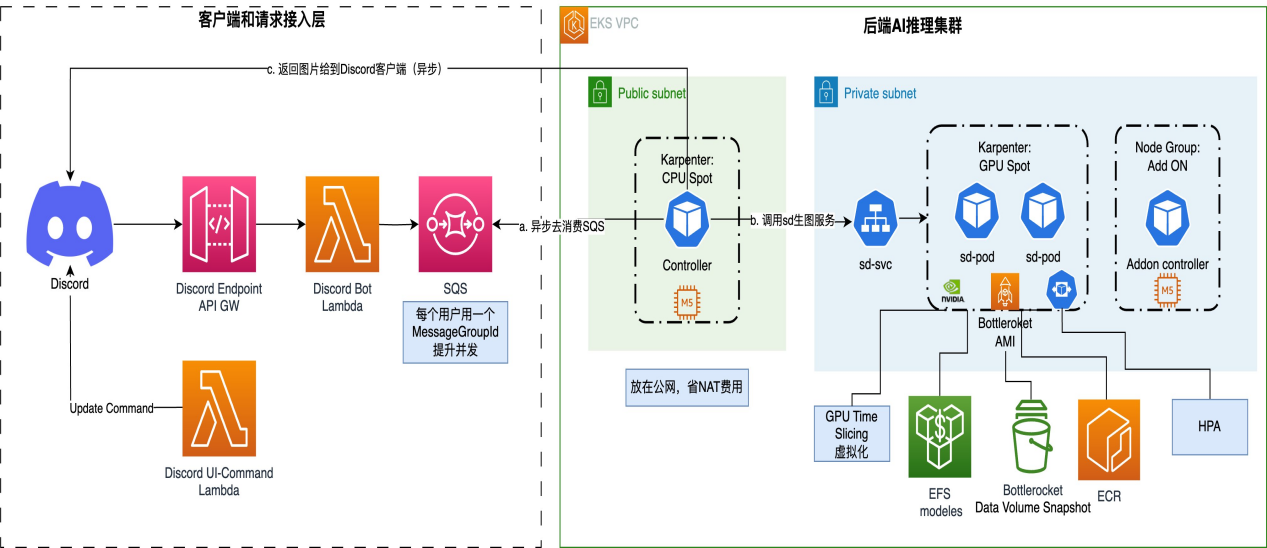
亚马逊云科技面向游戏运营活动的AI生图解决方案
随着Stable Diffusion等AI生图方案逐步普及,越来越多的场景被开发和落地。其中面向游戏C端玩家的AI生图营销活动场景正在被逐步验证:在某个游戏社区中,玩家一键从手机上传一张照片,AI会将自动识别该照片中的元素并替换成游戏中相应…...
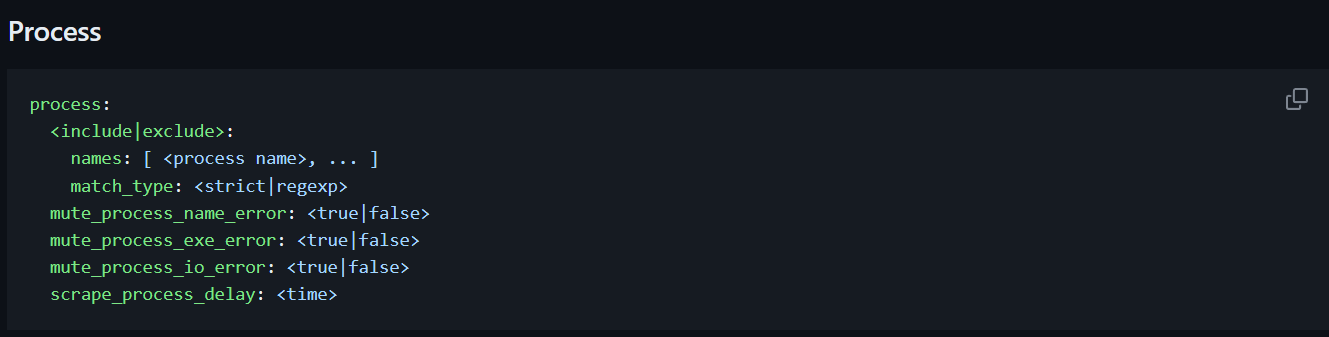
腾讯mini项目-【指标监控服务重构】2023-07-30
今日已办 调研 CPU & Memory Cadivisor Cadivisor -> Prometheus -> (Grafana / SigNoz Web) google/cadvisor: Analyzes resource usage and performance characteristics of running containers. (github.com) services:cadvisor:image: gcr.io/ca…...
Windows 下 MySQL 8.1 图形化界面安装、配置详解
首先我们下载安装包 官方下载链接: MySQL :: Begin Your Download 网盘链接: https://pan.baidu.com/s/1FOew6-93XpknB-bYDhDYPw 提取码: brys 外网下载慢的同学可以使用上述网盘链接 下载完成后我们双击安装包即可进入安装界面 点击next 勾选同意协议&#…...

WebRTC 源码 编译 iOS端
1. 获取依赖工具 首先,确保你已经安装了以下工具: GitDepot ToolsXcode(确保已安装命令行工具) 2. 下载 depot_tools 使用 git 克隆 depot_tools 并将其添加到你的 PATH 中: /path/to/depot_tools 替换为自己的路径…...

Python编程指南:利用HTTP和HTTPS适配器实现智能路由
嗨,爬虫大佬们!今天我要为大家分享一篇关于如何利用HTTP和HTTPS适配器来实现智能路由的Python编程指南。在现代互联网应用中,路由功能起着至关重要的作用,而利用Python编程语言实现智能路由则可以为我们的应用带来更高的灵活性和性…...

linux之kylin系统nginx的安装
一、nginx的作用 1.可做高性能的web服务器 直接处理静态资源(HTML/CSS/图片等),响应速度远超传统服务器类似apache支持高并发连接 2.反向代理服务器 隐藏后端服务器IP地址,提高安全性 3.负载均衡服务器 支持多种策略分发流量…...

day52 ResNet18 CBAM
在深度学习的旅程中,我们不断探索如何提升模型的性能。今天,我将分享我在 ResNet18 模型中插入 CBAM(Convolutional Block Attention Module)模块,并采用分阶段微调策略的实践过程。通过这个过程,我不仅提升…...

关于nvm与node.js
1 安装nvm 安装过程中手动修改 nvm的安装路径, 以及修改 通过nvm安装node后正在使用的node的存放目录【这句话可能难以理解,但接着往下看你就了然了】 2 修改nvm中settings.txt文件配置 nvm安装成功后,通常在该文件中会出现以下配置&…...

将对透视变换后的图像使用Otsu进行阈值化,来分离黑色和白色像素。这句话中的Otsu是什么意思?
Otsu 是一种自动阈值化方法,用于将图像分割为前景和背景。它通过最小化图像的类内方差或等价地最大化类间方差来选择最佳阈值。这种方法特别适用于图像的二值化处理,能够自动确定一个阈值,将图像中的像素分为黑色和白色两类。 Otsu 方法的原…...

React19源码系列之 事件插件系统
事件类别 事件类型 定义 文档 Event Event 接口表示在 EventTarget 上出现的事件。 Event - Web API | MDN UIEvent UIEvent 接口表示简单的用户界面事件。 UIEvent - Web API | MDN KeyboardEvent KeyboardEvent 对象描述了用户与键盘的交互。 KeyboardEvent - Web…...

华为云Flexus+DeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建
华为云FlexusDeepSeek征文|DeepSeek-V3/R1 商用服务开通全流程与本地部署搭建 前言 如今大模型其性能出色,华为云 ModelArts Studio_MaaS大模型即服务平台华为云内置了大模型,能助力我们轻松驾驭 DeepSeek-V3/R1,本文中将分享如何…...

使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台
🎯 使用 Streamlit 构建支持主流大模型与 Ollama 的轻量级统一平台 📌 项目背景 随着大语言模型(LLM)的广泛应用,开发者常面临多个挑战: 各大模型(OpenAI、Claude、Gemini、Ollama)接口风格不统一;缺乏一个统一平台进行模型调用与测试;本地模型 Ollama 的集成与前…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

系统掌握PyTorch:图解张量、Autograd、DataLoader、nn.Module与实战模型
本文较长,建议点赞收藏,以免遗失。更多AI大模型应用开发学习视频及资料,尽在聚客AI学院。 本文通过代码驱动的方式,系统讲解PyTorch核心概念和实战技巧,涵盖张量操作、自动微分、数据加载、模型构建和训练全流程&#…...
