机器学习算法: AdaBoost 详解
1. 集成学习概述
1.1. 定义
集成学习(Ensemble learning)就是将若干个弱分类器通过一定的策略组合之后产生一个强分类器。 弱分类器(Weak Classifier)指的就是那些分类准确率只比随机猜测略好一点的分类器,而强分类器( Strong Classifier)的分类准确率会高很多。这里的"强"&"弱"是相对的。某些书中也会把弱分类器称 为“基分类器”。
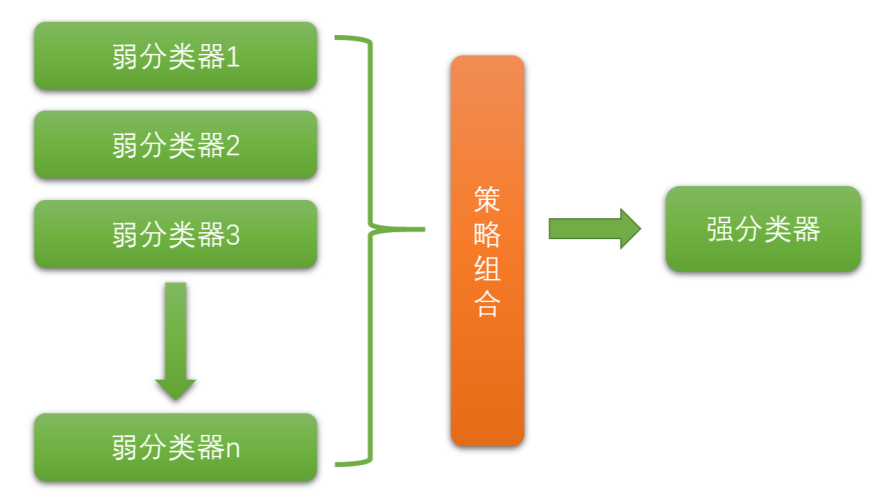
目前集成学习算法的流派主要有两种:
bagging boosting
1.2. bagging
装袋(bagging)又称自主聚集(bootstrap aggregating),是一种根据均匀概率分布从数据集中重复 抽样(有放回的)的技术。每个新数据集和原始数据集的大小相等。由于新数据集中的每个样本都是从 原始数据集中有放回的随机抽样出来的,所以新数据集中可能有重复的值,而原始数据集中的某些样本 可能根本就没出现在新数据集中。
bagging方法的流程,如下图所示:
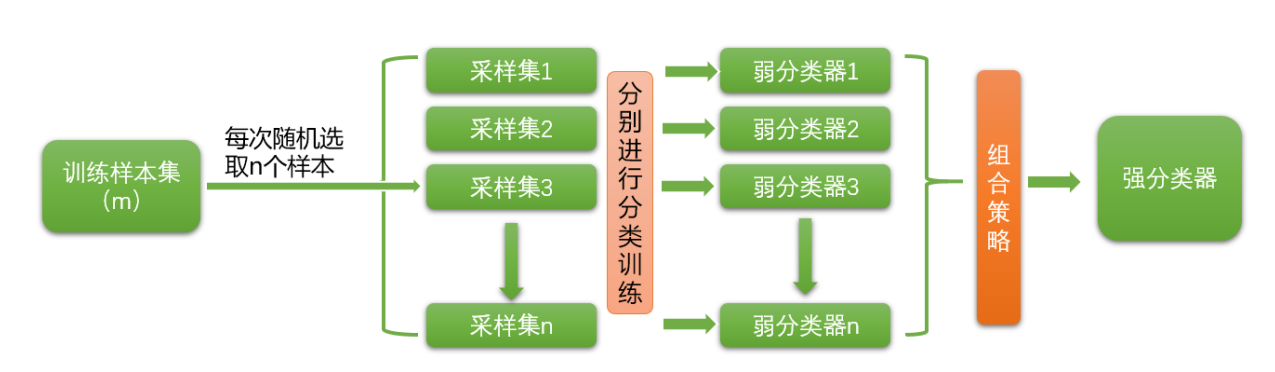
有放回的随机抽样:
自主采样法(Bootstap sampling),也就是说对于m个样本的原始数据集,每次 随机选取一个样本放入采样集,然后把这个样本重新放回原数据集中,然后再进行下一个样本的随机抽 样,直到一个采样集中的数量达到m,这样一个采样集就构建好了,然后我们可以重复这个过程,生成 n个这样的采样集。也就是说,最后形成的采样集,每个采样集中的样本可能是重复的,也可能原数据 集中的某些样本根本就没抽到,并且每个采样集中的样本分布可能都不一样。
根据有放回的随机抽样构造的n个采样集,我们就可以对它们分别进行训练,得到n个弱分类器,然后根 据每个弱分类器返回的结果,我们可以采用一定的组合策略得到我们最后需要的强分类器。
bagging方法的代表算法是随机森林,准确的来说,随机森林是bagging的一个特化进阶版,所谓的特 化是因为随机森林的弱学习器都是决策树。所谓的进阶是随机森林在bagging的样本随机采样基础上, 又加上了特征的随机选择,其基本思想没有脱离bagging的范畴。
1.3. boosting
boosting是一个迭代的过程,用来自适应地改变训练样本的分布,使得弱分类器聚焦到那些很难分类的 样本上。它的做法是给每一个训练样本赋予一个权重,在每一轮训练结束时自动地调整权重。
boosting方法的流程,如下图所示:
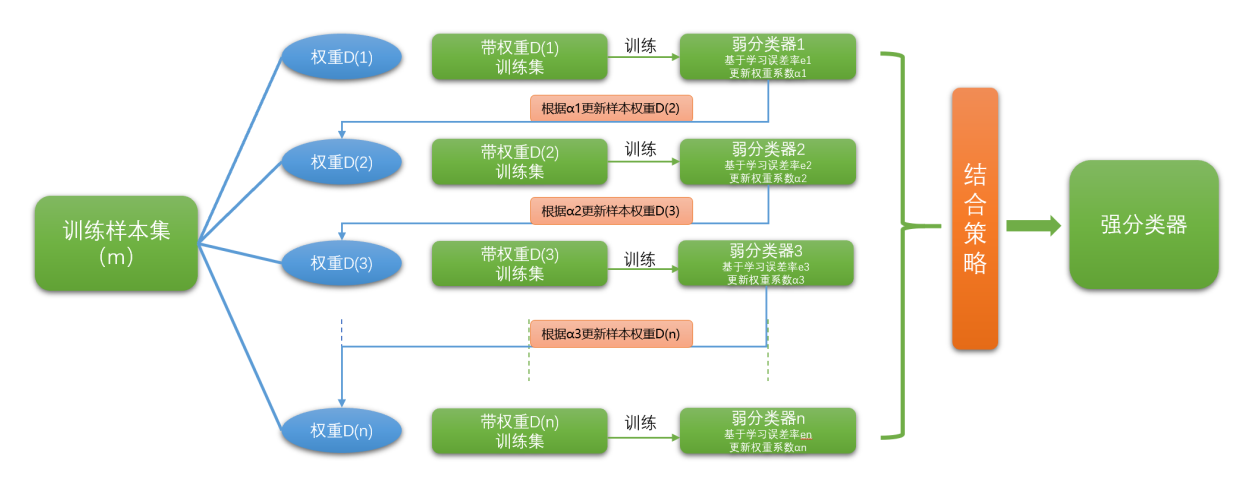
boosting方法的代表算法有Adaboost、GBDT、XGBoost算法
1.4. 结合策略
1.4.1. 平均法
对于数值类的回归预测问题,通常使用的结合策略是平均法,也就是说,对于若干个弱学习器的输出进 行平均得到最终的预测输出。
假设我们最终得到的n个弱分类器为
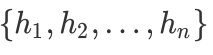
最简单的平均是算术平均,也就是说最终预测是
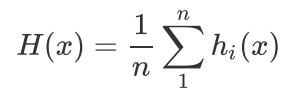
如果每个弱分类器有一个权重w,则最终预测是
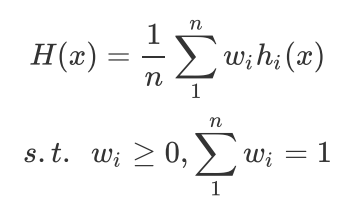
1.4.2. 投票法
对于分类问题的预测,我们通常使用的是投票法。假设我们的预测类别是
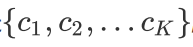
对于任意一个预测样本x,我们的n个弱学习器的预测结果分别是
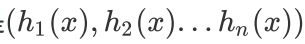
最简单的投票法是相对多数投票法,也就是我们常说的少数服从多数,也就是n个弱学习器的对样本x的 预测结果中,数量最多的类别 为最终的分类类别。如果不止一个类别获得最高票,则随机选择一个做 最终类别。
稍微复杂的投票法是绝对多数投票法,也就是我们常说的要票过半数。在相对多数投票法的基础上,不 光要求获得最高票,还要求票过半数。否则会拒绝预测。
更加复杂的是加权投票法,和加权平均法一样,每个弱学习器的分类票数要乘以一个权重,最终将各个 类别的加权票数求和,最大的值对应的类别为最终类别。
1.4.3. 学习法
前两种方法都是对弱学习器的结果做平均或者投票,相对比较简单,但是可能学习误差较大,于是就有 了学习法这种方法,对于学习法,代表方法是stacking,当使用stacking的结合策略时, 我们不是对弱 学习器的结果做简单的逻辑处理,而是再加上一层学习器,也就是说,我们将训练集弱学习器的学习结 果作为输入,将训练集的输出作为输出,重新训练一个学习器来得到最终结果。
在这种情况下,我们将弱学习器称为初级学习器,将用于结合的学习器称为次级学习器。对于测试集, 我们首先用初级学习器预测一次,得到次级学习器的输入样本,再用次级学习器预测一次,得到最终的 预测结果。
2. AdaBoost
Adaboost是adaptive boosting(自适应boosting)的缩写。算法步骤如下:
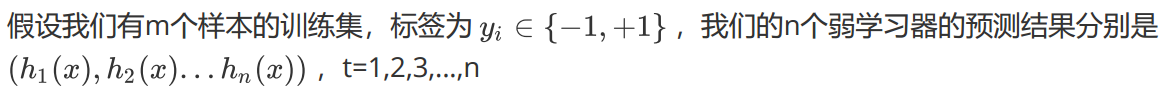
2.1. 计算样本权重
赋予训练集中每个样本一个权重,构成权重向量D,将权重向量D初始化相等值。设定我们有m个样本,每个样本的权重都相等,则权重为
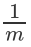
2.2. 计算错误率
在训练集上训练出一个弱分类器,并计算分类器的错误率:

2.3. 计算弱分离器权重
为当前分类器赋予权重值alpha,则alpha计算公式为:
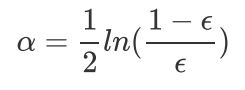
2.4. 调整权重值
根据上一次训练结果,调整权重值(上一次分对的权重降低,分错的权重增加
如果第i个样本被正确分类,则该样本权重更改为:
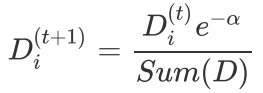
如果第i个样本被分错,则该样本权重更改为:
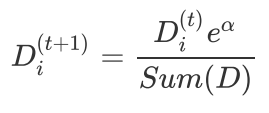
把上面两个公式汇整成一个:
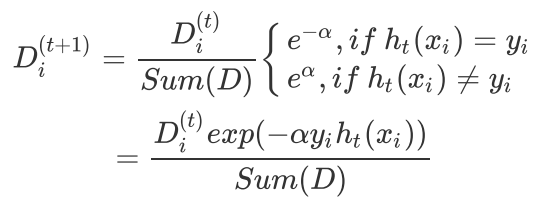
之后,在同一数据集上再一次训练弱分类器,然后循环上述过程,直到训练错误率为0,或者弱分类器 的数目达到指定值。
2.5. 结果
循环结束后,我们可以得到我们的强分类器的预测结果:
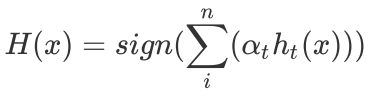
3. 基于单层决策树构建弱分类器
单层决策树(decision stump)也称决策树桩,是一种简单的决策树。我们已经讲过决策树的相 关原理了,接下来我们一起来构建一个单层决策树,它仅仅基于单个特征来做决策。由于这棵树只有一 次分裂过程,因此它实际上就是一个树桩。
3.1. 构建数据集
我们先构建一个简单数据集来确保我们写出的函数能够正常运行。
import pandas as pd
import numpy as np
# 获得特征矩阵和标签矩阵
def get_Mat(path):
dataSet = pd.read_table(path,header = None)
xMat = np.mat(dataSet.iloc[:,:-1].values)
yMat = np.mat(dataSet.iloc[:,-1].values).T
return xMat,yMat
xMat,yMat = get_Mat('simpdata.txt')
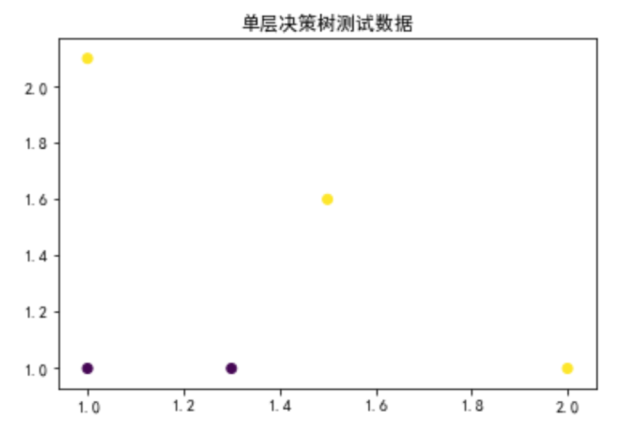
构建数据可视化函数,并运行查看数据分布
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['simhei']
%matplotlib inline
# 数据集可视化函数
def showPlot(xMat,yMat):
x=np.array(xMat[:,0])
y=np.array(xMat[:,1])
label = np.array(yMat)
plt.scatter(x,y,c=label)
plt.title('单层决策树测试数据')
plt.show()
showPlot(xMat,yMat)
3.2. 构建单层决策树
我们会建立两个函数来实现我们的单层决策树:
第一个函数用来测试是否有某个值小于或者大于我们正在测试的阈值。
"""
函数功能:单层决策树分类函数
参数说明:
xMat: 特征矩阵
i: 第i列,也就是第几个特征
Q: 阈值
S: 标志
返回:
re: 分类结果
"""
def Classify0(xMat,i,Q,S):
re = np.ones((xMat.shape[0],1)) # 初始化re为1
if S == 'lt':
re[xMat[:,i] <= Q] = -1 # 如果小于阈值,则赋值为-1
else:
re[xMat[:,i] > Q] = -1 # 如果大于阈值,则赋值为-1
return re
第二个函数稍微复杂一些,会在一个加权数据集中循环,并找到具有最低错误率的单层决策树
"""
函数功能:找到数据集上最佳的单层决策树
参数说明:
xMat:特征矩阵
yMat:标签矩阵
D:样本权重
返回:
bestStump:最佳单层决策树信息
minE:最小误差
bestClas:最佳的分类结果
"""
def get_Stump(xMat,yMat,D):
m,n = xMat.shape # m为样本个数,n为特征数
Steps = 10 # 初始化一个步数
bestStump = {} # 用字典形式来储存树桩信息
bestClas = np.mat(np.zeros((m,1))) # 初始化分类结果为1
minE = np.inf # 最小误差初始化为正无穷大
for i in range(n): # 遍历所有特征
Min = xMat[:,i].min() # 找到特征中最小值
Max = xMat[:,i].max() # 找到特征中最大值
stepSize = (Max - Min) / Steps # 计算步长
for j in range(-1, int(Steps)+1):
for S in ['lt', 'gt']: # 大于和小于的情况,均遍历。lt:less than,gt:greater than
Q = (Min + j * stepSize) # 计算阈值
re = Classify0(xMat, i, Q, S) # 计算分类结果
err = np.mat(np.ones((m,1))) # 初始化误差矩阵
err[re == yMat] = 0 # 分类正确的,赋值为0
eca = D.T * err # 计算误差
# print(f'切分特征: {i}, 阈值:{np.round(Q,2)}, 标志:{S}, 权重误差:{np.round(eca,3)}')
if eca < minE: # 找到误差最小的分类方式
minE = eca
bestClas = re.copy()
bestStump['特征列'] = i
bestStump['阈值'] = Q
bestStump['标志'] = S
return bestStump,minE,bestClas
测试函数并运行查看结果:
m = xMat.shape[0]
D = np.mat(np.ones((m, 1)) / m) # 初始化样本权重(每个样本权重相等)
bestStump,minE,bestClas= get_Stump(xMat,yMat,D)
4. AdaBoost代码
用python代码来实现完整版AdaBoost算法
"""
函数功能:基于单层决策树的AdaBoost训练过程
参数说明:
xMat:特征矩阵
yMat:标签矩阵
maxC:最大迭代次数
返回:
weakClass:弱分类器信息
aggClass:类别估计值(其实就是更改了标签的估计值)
"""
def Ada_train(xMat, yMat, maxC = 40):
weakClass = []
m = xMat.shape[0]
D = np.mat(np.ones((m, 1)) / m) # 初始化权重
aggClass = np.mat(np.zeros((m,1)))
for i in range(maxC):
Stump, error, bestClas = get_Stump(xMat, yMat,D) # 构建单层决策树
# print(f"D:{D.T}")
alpha=float(0.5 * np.log((1 - error) / max(error, 1e-16))) # 计算弱分类器权重alpha
Stump['alpha'] = np.round(alpha,2) # 存储弱学习算法权重,保留两位小数
weakClass.append(Stump) # 存储单层决策树
# print("bestClas: ", bestClas.T)
expon = np.multiply(-1 * alpha *yMat, bestClas) # 计算e的指数项
D = np.multiply(D, np.exp(expon))
D = D / D.sum() # 根据样本权重公式,更新样本权重
aggClass += alpha * bestClas #更新累计类别估计值
# print(f"aggClass: {aggClass.T}" )
aggErr = np.multiply(np.sign(aggClass) != yMat, np.ones((m,1)))# 计算误差
errRate = aggErr.sum() / m
# print(f"分类错误率: {errRate}")
if errRate == 0: break # 误差为0,退出循环
return weakClass, aggClass
运行函数,查看结果:
weakClass, aggClass =Ada_train(xMat, yMat, maxC = 40)
weakClass
aggClass
5. 基于AdaBoost的分类
这里我们使用弱分类器的加权求和来计算最后的结果。
"""
函数功能:AdaBoost分类函数
参数说明:
data: 待分类样例
classifys:训练好的分类器
返回:
分类结果
"""
def AdaClassify(data,weakClass):
dataMat = np.mat(data)
m = dataMat.shape[0]
aggClass = np.mat(np.zeros((m,1)))
for i in range(len(weakClass)): # 遍历所有分类器,进行分类
classEst = Classify0(dataMat,
weakClass[i]['特征列'],
weakClass[i]['阈值'],
weakClass[i]['标志'])
aggClass += weakClass[i]['alpha'] * classEst
# print(aggClass)
return np.sign(aggClass)
结果
AdaClassify([0,0],weakClass)
本文由 mdnice 多平台发布
相关文章:

机器学习算法: AdaBoost 详解
1. 集成学习概述 1.1. 定义 集成学习(Ensemble learning)就是将若干个弱分类器通过一定的策略组合之后产生一个强分类器。 弱分类器(Weak Classifier)指的就是那些分类准确率只比随机猜测略好一点的分类器,而强分类器&…...

6.824lab1总结
目录总体概要核心结构体coordinator思路:任务池管理RPC函数worker思路:实现细节总体概要 程序主要由mrcoordinator.go、mrworker.go为启动模块。 mrcoordinator.go: 启动rpc服务,循环等待m.Done()为true时退出。mrwoker.go:调用mr.worker(mapf, reduce…...

NIO蔚来 面试——IP地址你了解多少?
目录 前言 1、IP地址 1.1、什么是IP地址 1.2、IP地址的格式 1.2.1、32位二进制数表示IP地址,够用吗? 1.3、IP地址的组成 1.4、为什么会出现IPv6 1.4.1、为什么IPv6还没有大量普及呢? 1.5、子网掩码 1.6、特殊的IP地址 2、路由选择 …...

Gluten 首次开源技术沙龙成功举办,更多新能力值得期待
2023年2月17日,由 Kyligence 主办的 Gluten 首次开源技术沙龙在上海成功举办,本期沙龙特邀来自 Intel、BIGO、eBay、阿里、华为和 Kyligence 等行业技术专家齐聚一堂,共同探讨了向量化执行引擎框架 Gluten 现阶段社区的重点开发成果和未来的发…...

springboot+redis+lua实现限流
Redis 除了做缓存,还能干很多很多事情:分布式锁、限流、处理请求接口幂等性。。。太多太多了~今天想和小伙伴们聊聊用 Redis 处理接口限流。1. 准备工作首先我们创建一个 Spring Boot 工程,引入 Web 和 Redis 依赖,同时…...

线段树总结
文章目录参考文档题目线段树实现单点修改,区间求值模板题目308. 二维区域和检索 - 可变区间修改,区间求值1. 掉落的方块(区间开点)2. 维护序列3. 一个简单的问题24. 天际线问题动态开点1. 区间和个数(单点修改开点)问题以及注意事…...
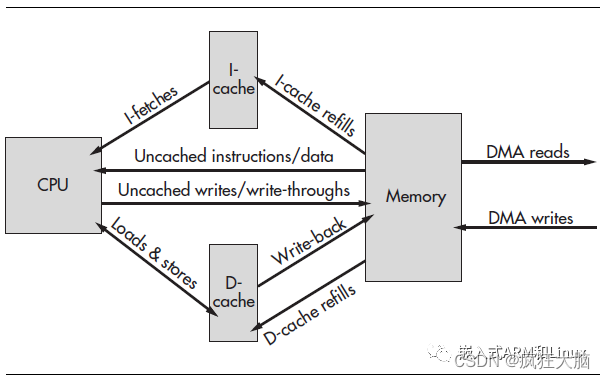
龙芯GS232(MIPS 32)架构cache管理笔记
1 mips32架构 MIPS架构是一种基于精简指令集(Reduced Instruction Set Computer,RISC)的计算机处理器架构。MIPS架构由MIPS Technologies公司在1981年开发,并在1984年发布了第一款MIPS处理器。 MIPS架构的特点包括: …...

js去重
<script>let arr [{ id: 0, name: "张三" },{ id: 1, name: "李四" },{ id: 2, name: "王五" },{ id: 3, name: "赵六" },{ id: 1, name: "孙七" },{ id: 2, name: "周八" },{ id: 2, name: "吴九&qu…...
小白都能看懂的C语言入门教程
文章目录C语言入门教程1. 第一个C语言程序HelloWorld2. C语言的数据类型3. 常量变量的使用4. 自定义标识符#define5. 枚举的使用6. 字符串和转义字符7. 判断和循环8. 函数9. 数组的使用10. 操作符的使用11. 结构体12. 指针的简单使用C语言入门教程 1. 第一个C语言程序HelloWor…...
leetcode 21~30 学习经历
leetcode 21~30 学习经历21. 合并两个有序链表22. 括号生成23. 合并K个升序链表24. 两两交换链表中的节点25. K 个一组翻转链表26. 删除有序数组中的重复项27. 移除元素28. 找出字符串中第一个匹配项的下标29. 两数相除30. 串联所有单词的子串小结21. 合并两个有序链表 将两个升…...

让ArcMap变得更加强大,用python执行地理处理以及编写自定义脚本工具箱
文章目录一、用python执行地理处理工具1.1 例:乘以0.00011.2 例:裁剪栅格1.3 哪里查看调用某工具的代码?二、用python批量执行地理处理工具2.1 必需的python语法知识for循环语句缩进的使用注释的使用2.2 一个批处理栅格的代码模板三、创建自定…...

SAP 项目实施阶段全过程
在sap实施项目的周期和步骤上,根据各公司对业务的理解不同,也被划分为各个阶段,但其中由普华永道提出的分七步走,个人觉得对刚进入这一行业的人很有帮助,接下来一起分享和讨论下: sap实施项目生命周期&…...

idea中的Maven导包失败问题解决总结
idea中的Maven导包失败问题解决总结 先确定idea和Maven 的配置文件settings 没有问题 找到我们本地的maven仓库,默认的maven仓库路径是在\C:\Users\用户名.m2下 有两个文件夹,repositotry是放具体jar包的,根据报错包的名,找对应文…...
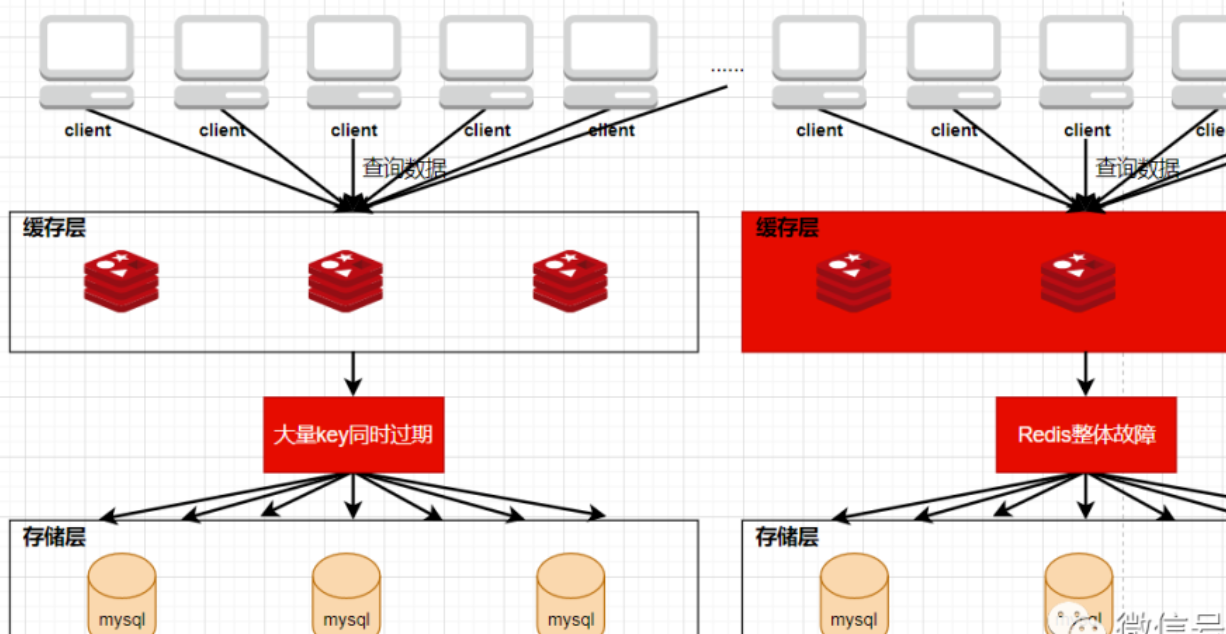
REDIS中的缓存穿透,缓存击穿,缓存雪崩原因以及解决方案
需求引入一般在项目的开发中,都是使用关系型数据库来进行数据的存储,通常不会存在什么高并发的情况,可是一旦涉及大数据量的需求,比如商品抢购,网页活动导致的主页访问量瞬间增大,单一使用关系型数据库来保存数据的系统…...
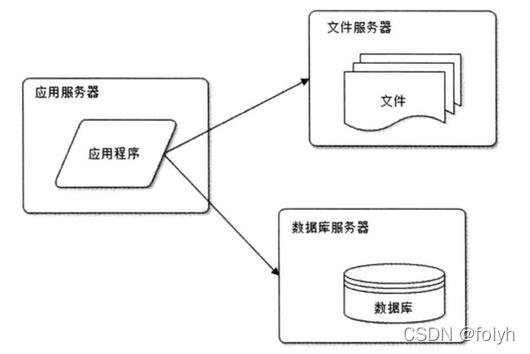
数据库及缓存之MySQL(一)
思维导图 常见知识点 1.mysql存储引擎: 2.innodb与myisam区别: 3.表设计字段选择: 4.mysql的varchar(M)最多存储数据: 5.事务基本特性: 6.事务并发引发问题: 7.mysql索引: 8.三星索引…...

项目管理中,项目经理需要具备哪些能力?
项目经理是团队的领导者,是带领项目团队对项目进行策划、执行,完成项目目标,对于项目经理来说,想要有序推进项目,使项目更成功,光有理论知识是不够的,也要具备这些能力: 1、分清主…...

itk中的一些图像处理
文章目录1.BinomialBlurImageFilter计算每个维度上的最近邻居平均值2.高斯平滑3.图像的高阶导数 RecursiveGaussianImageFilter4.均值滤波5.中值滤波6.离散高斯平滑7.曲率驱动流去噪图像 CurvatureFlowImageFilter8.由参数alpha和beta控制的幂律自适应直方图均衡化9.Canny 边缘…...
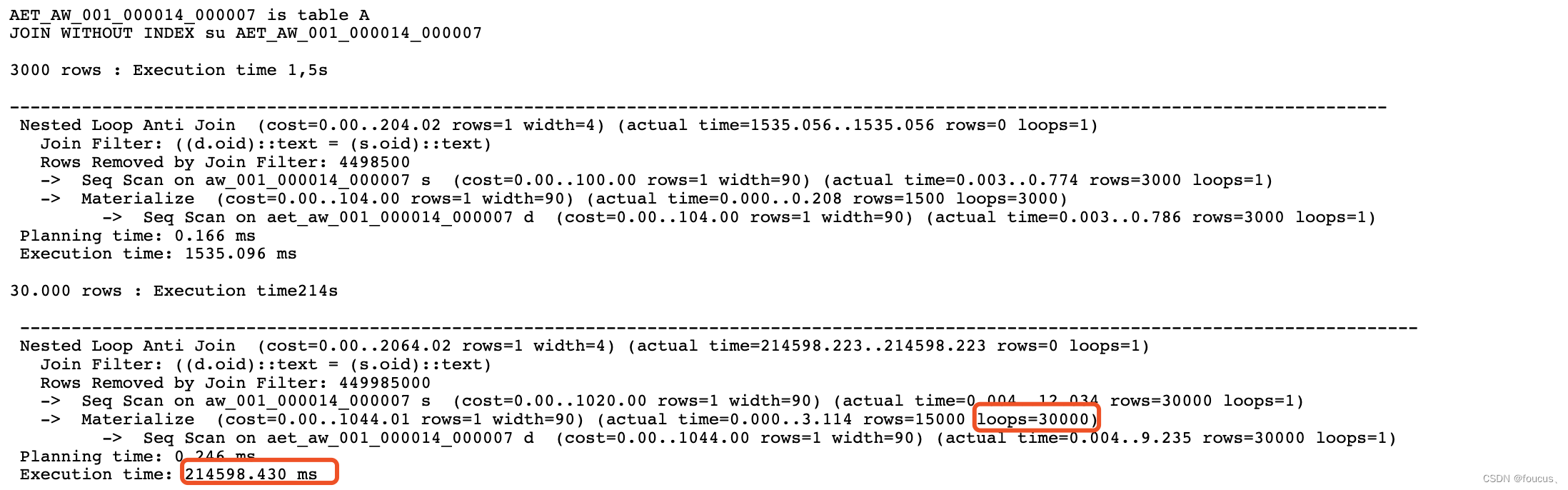
Endless lseek导致的SQL异常
最近碰到同事咨询的一个问题,在执行一个函数时,发现会一直卡在那里。 strace抓了下发现会话一直在执行lseek,大致情况如下: 16:13:55.451832 lseek(33, 0, SEEK_END) 1368064 <0.000037> 16:13:55.477216 lseek(33, 0, SE…...
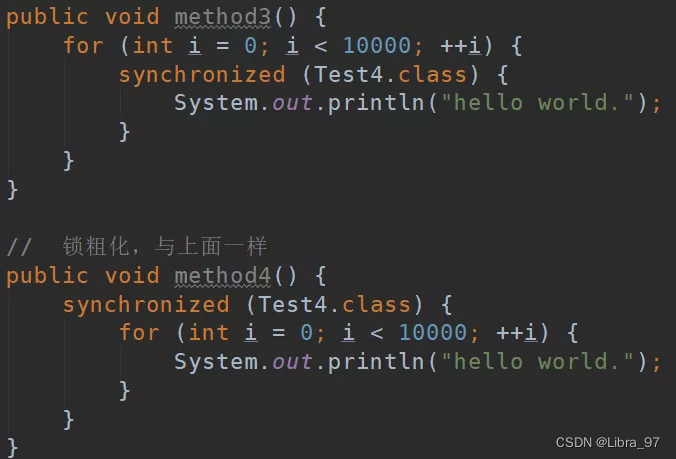
JUC-day01
JUC-day01 什么是JUC线程的状态: wait sleep关键字:同步锁 原理(重点)Lock接口: ReentrantLock(可重入锁)—>AQS CAS线程之间的通讯 1 什么是JUC 1.1 JUC简介 在Java中,线程部分是一个重点,本篇文章说的JUC也是关于线程的。JUC就是java.util .con…...
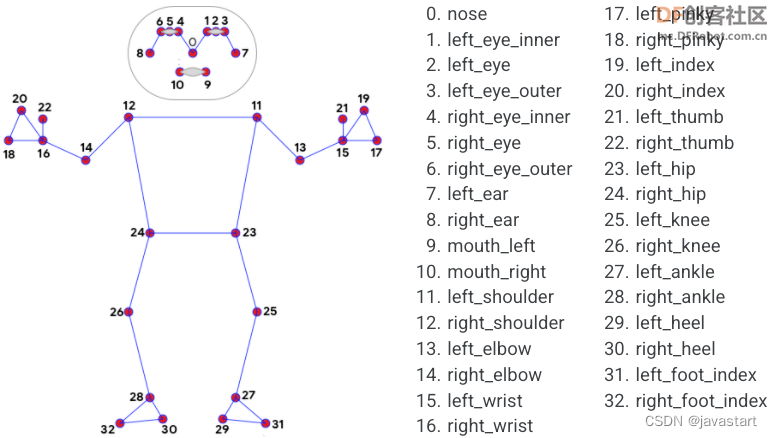
Mind+Python+Mediapipe项目——AI健身之跳绳
原文:MindPythonMediapipe项目——AI健身之跳绳 - DF创客社区 - 分享创造的喜悦 【项目背景】跳绳是一个很好的健身项目,为了获知所跳个数,有的跳绳上会有计数器。但这也只能跳完这后看到,能不能在跳的过程中就能看到,…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

SkyWalking 10.2.0 SWCK 配置过程
SkyWalking 10.2.0 & SWCK 配置过程 skywalking oap-server & ui 使用Docker安装在K8S集群以外,K8S集群中的微服务使用initContainer按命名空间将skywalking-java-agent注入到业务容器中。 SWCK有整套的解决方案,全安装在K8S群集中。 具体可参…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

可靠性+灵活性:电力载波技术在楼宇自控中的核心价值
可靠性灵活性:电力载波技术在楼宇自控中的核心价值 在智能楼宇的自动化控制中,电力载波技术(PLC)凭借其独特的优势,正成为构建高效、稳定、灵活系统的核心解决方案。它利用现有电力线路传输数据,无需额外布…...

Spring AI 入门:Java 开发者的生成式 AI 实践之路
一、Spring AI 简介 在人工智能技术快速迭代的今天,Spring AI 作为 Spring 生态系统的新生力量,正在成为 Java 开发者拥抱生成式 AI 的最佳选择。该框架通过模块化设计实现了与主流 AI 服务(如 OpenAI、Anthropic)的无缝对接&…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

成都鼎讯硬核科技!雷达目标与干扰模拟器,以卓越性能制胜电磁频谱战
在现代战争中,电磁频谱已成为继陆、海、空、天之后的 “第五维战场”,雷达作为电磁频谱领域的关键装备,其干扰与抗干扰能力的较量,直接影响着战争的胜负走向。由成都鼎讯科技匠心打造的雷达目标与干扰模拟器,凭借数字射…...

【Java学习笔记】BigInteger 和 BigDecimal 类
BigInteger 和 BigDecimal 类 二者共有的常见方法 方法功能add加subtract减multiply乘divide除 注意点:传参类型必须是类对象 一、BigInteger 1. 作用:适合保存比较大的整型数 2. 使用说明 创建BigInteger对象 传入字符串 3. 代码示例 import j…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...
