c++分层最短路(洛谷飞行路线)acwing版
分层最短路算法是在SPFA算法的基础上,将每个点分成若干层,从而使得每个点之间的转移只在同一层次或上下两个相邻层次之间进行,减少了每轮的迭代次数,优化了算法的效率。
#include <iostream>
#include <cstdio>
#include <cstring>
#include <queue>using namespace std;const int MAXN = 10005;
const int MAXM = 100005;
const int INF = 0x3f3f3f3f;struct Edge {int to, nxt, w;
} e[MAXM];int head[MAXN], tot;
int dis[MAXN], vis[MAXN];inline void add(int u, int v, int w) {e[++tot].nxt = head[u];e[tot].to = v;e[tot].w = w;head[u] = tot;
}void spfa(int s) {memset(dis, 0x3f, sizeof(dis));dis[s] = 0;queue<int> q;q.push(s);while (!q.empty()) {int u = q.front();q.pop();vis[u] = false;for (int i = head[u]; i; i = e[i].nxt) {int v = e[i].to;if (dis[v] > dis[u] + e[i].w) {dis[v] = dis[u] + e[i].w;if (!vis[v]) {q.push(v);vis[v] = true;}}}}
}int main() {int n, m;scanf("%d%d", &n, &m);tot = 0;memset(head, 0, sizeof(head));for (int i = 1; i <= m; ++i) {int u, v, w;scanf("%d%d%d", &u, &v, &w);add(u, v, w);}int s, t;scanf("%d%d", &s, &t);spfa(s);printf("%d\n", dis[t]);return 0;
}
int layer[MAXN]; //记录每个点所在的层次
int check_layer[MAXN]; //记录每个点是否在队列中void layer_spfa(int s) {memset(dis, 0x3f, sizeof(dis));dis[s] = 0;layer[s] = 0;queue<int> q;q.push(s);check_layer[s] = true;while (!q.empty()) {int u = q.front();q.pop();check_layer[u] = false;for (int i = head[u]; i; i = e[i].nxt) {int v = e[i].to;if (layer[u] == layer[v]) {if (dis[v] > dis[u] + e[i].w) {dis[v] = dis[u] + e[i].w;if (!check_layer[v]) {q.push(v);check_layer[v] = true;}}} else if (layer[v] > layer[u]) { //分层if (dis[v] > dis[u] + e[i].w) {dis[v] = dis[u] + e[i].w;layer[v] = layer[u] + 1;if (!check_layer[v]) {q.push(v);check_layer[v] = true;}}}}}
}
先看题目:
Alice 和 Bob 现在要乘飞机旅行,他们选择了一家相对便宜的航空公司。该航空公司一共在 nn 个城市设有业务,设这些城市分别标记为 00 到 n-1n−1,一共有 mm 种航线,每种航线连接两个城市,并且航线有一定的价格。
Alice 和 Bob 现在要从一个城市沿着航线到达另一个城市,途中可以进行转机。航空公司对他们这次旅行也推出优惠,他们可以免费在最多 kk 种航线上搭乘飞机。那么 Alice 和 Bob 这次出行最少花费多少?
输入格式
第一行三个整数 n,m,kn,m,k,分别表示城市数,航线数和免费乘坐次数。
接下来一行两个整数 s,ts,t,分别表示他们出行的起点城市编号和终点城市编号。
接下来 mm 行,每行三个整数 a,b,ca,b,c,表示存在一种航线,能从城市 aa 到达城市 bb,或从城市 bb 到达城市 aa,价格为 cc。
输出格式
输出一行一个整数,为最少花费。
输入样例:
5 6 1
0 4
0 1 5
1 2 5
2 3 5
3 4 5
2 3 3
0 2 100输出样例:
8先给出具体代码:
#include<cstring>
#include<iostream>
#include<queue>using namespace std;typedef pair<int, int> PII;const int N = 2100010, INF = 0x3f3f3f3f;int n, m, k, s, t;
int dist[N];
int h[N], w[N], e[N], ne[N], idx;
bool st[N];void add(int a, int b, int c)
{e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++;
}void dijkstra(int u)
{memset(dist, INF, sizeof dist);dist[u] = 0;priority_queue<PII, vector<PII>, greater<PII>> heap;heap.push({0, u});while(heap.size()){auto t = heap.top();heap.pop();int ver = t.second ,distance = t.first;if(st[ver]) continue;st[ver] = true;for(int i = h[ver]; ~i; i = ne[i]){int j = e[i];if(dist[j] > distance + w[i]){dist[j] = distance + w[i];heap.push({dist[j], j});}}}
}int main()
{cin >> n >> m >> k >> s >> t;memset(h, -1, sizeof h);while(m --){int a, b, c;scanf("%d%d%d", &a, &b ,&c);add(a, b, c), add(b, a, c);for(int j = 1; j <= k; j ++){add(j * n + a, j * n + b, c);add(j * n + b, j * n + a, c);add((j - 1) * n + a, j * n + b, 0);add((j - 1) * n + b, j * n + a, 0);}}for(int i = 0; i < k; i ++) add(i * n + t, (i + 1) * n + t, 0);dijkstra(s);printf("%d\n", dist[n * k + t]);return 0;
}1:解释数据:2≤n≤10^4,1≤m≤10^5,0≤k≤10,0≤s, t, a, b<n, a != b, 0≤c≤10^3
本来数据最大值是m,双向边开两倍就可以,但是这里是分层建图,最多有十层,所以要再乘以十
2:初始化h数组
3、加边,下面的是分层建图
建图:从0到k层建k+1张图
各层之间从上到下建边花费为0
为防止使用小于k次权力就到达终点,在每层的终点间建花费为0的边连起来
4、dijkstra堆优化版的模板
5、答案输出:到k层的终点为答案
相关文章:
acwing版)
c++分层最短路(洛谷飞行路线)acwing版
分层最短路算法是在SPFA算法的基础上,将每个点分成若干层,从而使得每个点之间的转移只在同一层次或上下两个相邻层次之间进行,减少了每轮的迭代次数,优化了算法的效率。 #include <iostream> #include <cstdio> #inc…...

Python bs4 BeautifulSoup库使用记录
目录 介绍 安装 初始化 解析器 使用方法 优势 Python标准库 lxml HTML lxml XML html5lib 格式化输出 对象 tag Name 多值属性 其他方法 NavigableString BeautifulSoup Comment 遍历 子节点 父节点 兄弟节点 回退和前进 搜索 过滤器 字符串 正则表达…...
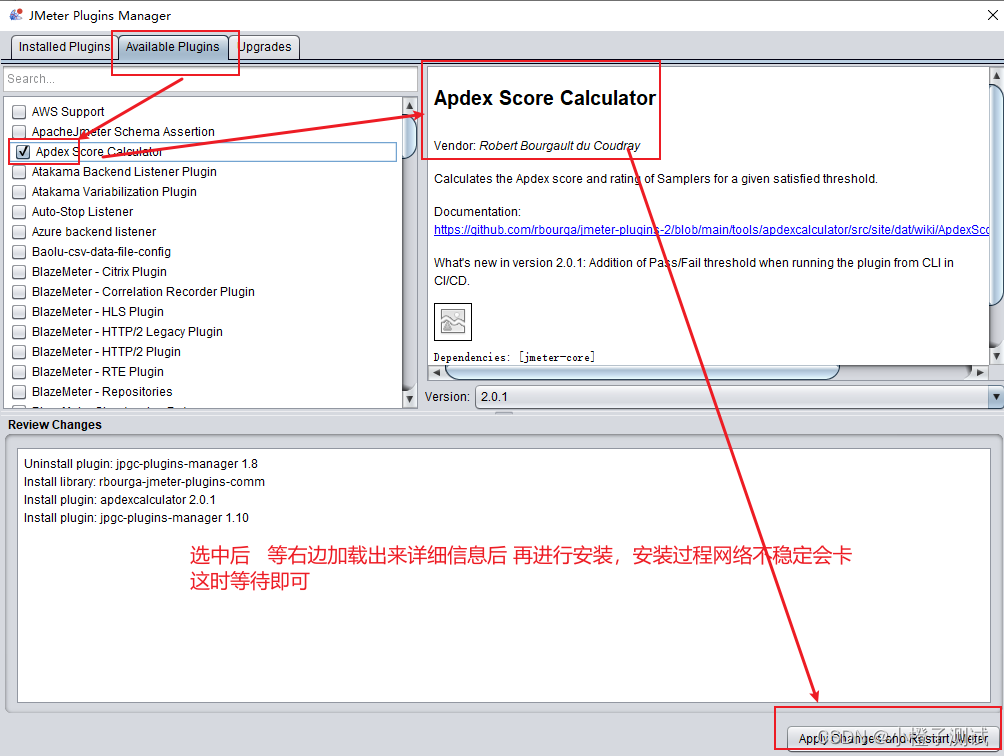
Jmeter系列-插件安装(5)
前言 jmeter4.0以上,如现在最新的5.2.1版本是有集成插件的只需要在官网下载 plugins-manager.jar 包,放在jmeter安装路径的lib/ext目录下即可使用:https://jmeter-plugins.org/install/Install/但并不能满足所有需求,仍然需要安装…...

spring aop源码解析
spring知识回顾 spring的两个重要功能:IOC、AOP,在ioc容器的初始化过程中,会触发2种处理器的调用, 前置处理器(BeanFactoryPostProcessor)后置处理器(BeanPostProcessor)。 前置处理器的调用时机是在容器基本创建完成时ÿ…...
控制物体移动、旋转)
使用Unity的Input.GetAxis(““)控制物体移动、旋转
使用Unity的Input.GetAxis("")控制物体移动、旋转 Input.GetAxis("") 是 Unity 引擎中的一个方法,用于获取游戏玩家在键盘或游戏手柄上输入的某个轴(Axis)的值。这里的 "" 是一个字符串参数,表示要…...

【CSS】画个三角形或圆形或环
首先通过调整边框,我们可以发现一些端倪 <!DOCTYPE html> <html><head><meta charset"utf-8"><title></title></head><style>.box{width: 150px;height:150px;border: 50px solid black;}</style&g…...

AI项目六:基于YOLOV5的CPU版本部署openvino
若该文为原创文章,转载请注明原文出处。 一、CPU版本DEMO测试 1、创建一个新的虚拟环境 conda create -n course_torch_openvino python3.8 2、激活环境 conda activate course_torch_openvino 3、安装pytorch cpu版本 pip install torch torchvision torchau…...

记录YDLidar驱动包交叉编译时出现的一点问题
由于一不小心把交叉编译的系统根目录破坏了,所以一股脑将交叉编译系统根目录全删了重新安装,安装后,交叉编译发现ydlidar的ros包驱动出现了库无法链接的错误(刚刚还是好好的),但是又想不起来之前是怎么解决的了,所以还…...

嵌入式学习笔记(32)S5PV210的向量中断控制器
6.6.1异常处理的2个阶段 可以将异常处理分为2个阶段来理解。第一个阶段是异常向量表跳转;第二个阶段是进入了真正的异常处理程序irq_handler之后的部分。 6.6.2回顾:中断处理的第一个阶段(异常向量表跳转阶段)处理 (…...

linux下安装qt、qt触摸屏校准tslib
linux下安装qt 在 Linux 系统下安装 Qt,可以通过以下步骤进行操作:1. 下载 Qt 安装包:首先,你需要从 Qt 官方网站(https://www.qt.io/)下载适用于 Linux 的 Qt 安装包。选择与你的系统和需求相匹配的版本&…...

C++之unordered_map,unordered_set模拟实现
unordered_map,unordered_set模拟实现 哈希表源代码哈希表模板参数的控制仿函数增加正向迭代器实现*运算符重载->运算符重载运算符重载! 和 运算符重载begin()与end()实现 unordered_set实现unordered_map实现map/set 与 unordered_map/unordered_set对比哈希表…...

React Router,常用API有哪些?
react-router React Router是一个用于构建单页面应用程序(SPA)的库,它是用于管理React应用中页面导航和路由的工具。SPA是一种Web应用程序类型,它在加载初始页面后,通过JavaScript来动态加载并更新页面内容࿰…...

JVM类加载和双亲委派机制
当我们用java命令运行某个类的main函数启动程序时,首先需要通过类加载器把类加载到JVM,本文主要说明类加载机制和其具体实现双亲委派模式。 一、类加载机制 类加载过程: 类加载的过程是将类的字节码加载到内存中的过程,主要包括…...

P-MVSNet ICCV-2019 学习笔记总结 译文 深度学习三维重建
文章目录 5 P-MVSNet ICCV-20195.0 主要特点5.1 文章概述5.2 研究方法5.2.1 特征提取5.2.2 学习局域匹配置信5.2.3 深度图预测5.2.4 Loss方程MVSNet系列最新顶刊 对比总结5 P-MVSNet ICCV-2019 深度学习三维重建 P-MVSNet-ICCV-2019(原文、译文、批注) 下载 5.0 主要特点 …...
vueshowpdf 移动端pdf文件预览
1、安装 npm install vueshowpdf -S2、参数 属性说明类型默认值v-model是否显示pdf--pdfurlpdf的文件地址String- scale 默认放大倍数 Number1.2 minscale 最小放大倍数 Number0.8 maxscale 最大放大倍数 Number2 3、事件 名称说明回调参数closepdf pdf关闭事件-pdferr文…...

C#根据excel文件中的表头创建数据库表
C#根据excel文件中的表头创建数据库表 private void button1_Click(object sender, EventArgs e){string tableName tableNameTextBox.Text;string connectionString "";using (OpenFileDialog openFileDialog new OpenFileDialog()){openFileDialog.Filter &quo…...
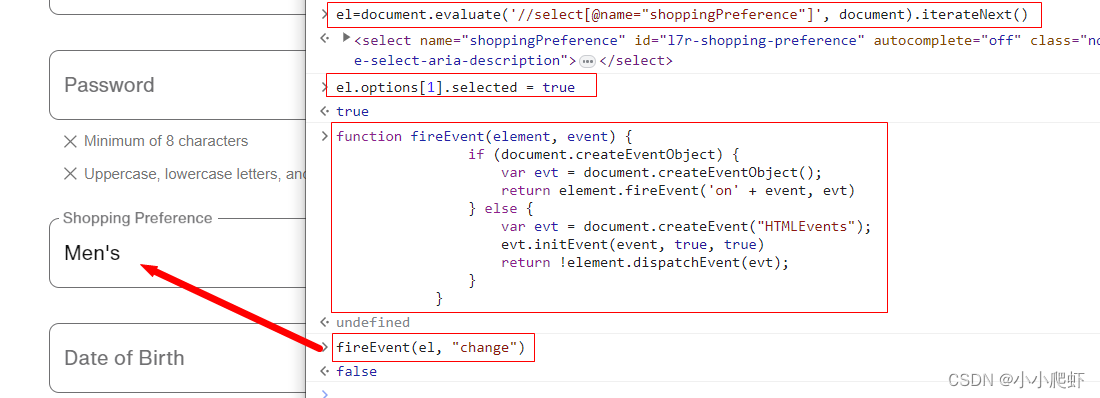
js通过xpath定位元素并且操作元素以下拉框select为例
js也可以使用xpath定位元素,现在实例讲解。 页面上有一个下拉框,里面内容有三个,用F12看一下 一、使用xpath定位这个下拉框select eldocument.evaluate(//select[name"shoppingPreference"], document).iterateNext()二、为下拉框…...
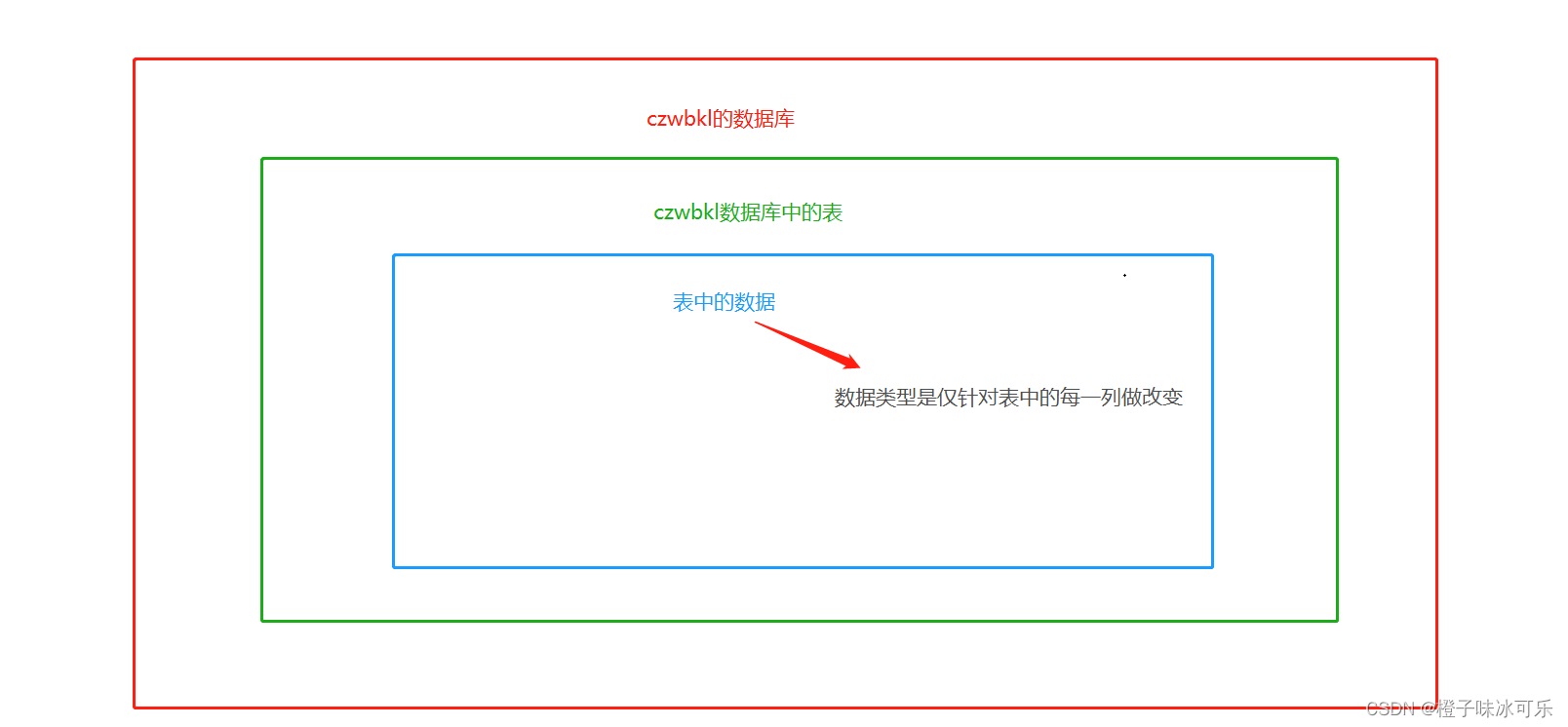
数据类型
目录 1.数值类型 整数类型 int 小数类型 double 2.字符类型 固定长度字符串 char 可变长度字符串 varchar 3.日期时间类型 日期类型:date 日期时间类型:datetime MySQL从小白到总裁完整教程目录:https://blog.csdn.net/weixin_67859959/article…...

vue 模板应用
一,模板应用也就是对DOM的操作 二,如何使用 通过标签里面添加ref 和vue中使用 this.$refs.ref的名字.操作 进行使用 <template><h3>模板引用</h3><div ref"cont" class"cont">{{ content }}</div>&…...
Golang教程与Gin教程合集,入门到实战
GolangGin框架GormRbac微服务仿小米商城项目实战视频教程Docker Swarm K8s云原生分布式部署 介绍: Go即Golang,是Google公司2009年11月正式对外公开的一门编程语言,它不仅拥有静态编译语言的安全和高性能,而 且又达到了动态语言开…...

XCTF-web-easyupload
试了试php,php7,pht,phtml等,都没有用 尝试.user.ini 抓包修改将.user.ini修改为jpg图片 在上传一个123.jpg 用蚁剑连接,得到flag...

springboot 百货中心供应链管理系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,百货中心供应链管理系统被用户普遍使用,为方…...

React第五十七节 Router中RouterProvider使用详解及注意事项
前言 在 React Router v6.4 中,RouterProvider 是一个核心组件,用于提供基于数据路由(data routers)的新型路由方案。 它替代了传统的 <BrowserRouter>,支持更强大的数据加载和操作功能(如 loader 和…...

【解密LSTM、GRU如何解决传统RNN梯度消失问题】
解密LSTM与GRU:如何让RNN变得更聪明? 在深度学习的世界里,循环神经网络(RNN)以其卓越的序列数据处理能力广泛应用于自然语言处理、时间序列预测等领域。然而,传统RNN存在的一个严重问题——梯度消失&#…...

ServerTrust 并非唯一
NSURLAuthenticationMethodServerTrust 只是 authenticationMethod 的冰山一角 要理解 NSURLAuthenticationMethodServerTrust, 首先要明白它只是 authenticationMethod 的选项之一, 并非唯一 1 先厘清概念 点说明authenticationMethodURLAuthenticationChallenge.protectionS…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

关于uniapp展示PDF的解决方案
在 UniApp 的 H5 环境中使用 pdf-vue3 组件可以实现完整的 PDF 预览功能。以下是详细实现步骤和注意事项: 一、安装依赖 安装 pdf-vue3 和 PDF.js 核心库: npm install pdf-vue3 pdfjs-dist二、基本使用示例 <template><view class"con…...

保姆级【快数学会Android端“动画“】+ 实现补间动画和逐帧动画!!!
目录 补间动画 1.创建资源文件夹 2.设置文件夹类型 3.创建.xml文件 4.样式设计 5.动画设置 6.动画的实现 内容拓展 7.在原基础上继续添加.xml文件 8.xml代码编写 (1)rotate_anim (2)scale_anim (3)translate_anim 9.MainActivity.java代码汇总 10.效果展示 逐帧…...

从零开始了解数据采集(二十八)——制造业数字孪生
近年来,我国的工业领域正经历一场前所未有的数字化变革,从“双碳目标”到工业互联网平台的推广,国家政策和市场需求共同推动了制造业的升级。在这场变革中,数字孪生技术成为备受关注的关键工具,它不仅让企业“看见”设…...
